مدار سه فاز — از صفر تا صد

سیستم‌های سه‌فاز، نسبت به سیستم‌های تک‌فاز، مزایای اقتصادی و عملکردی فراوانی دارند. برای مثال، در یک توان خروجی مشابه، ژنراتورهای سه‌فاز ارزان‌تر از ژنراتورهای تک‌فاز هستند، توان تولیدی آن‌ها یکنواخت است و ارتعاش و نویز کمتری دارند. در مدار سه فاز، سه منبع توان ac وجود دارد و کاربرد آن‌ در صنعت بسیار زیاد است. یکی از این کاربردها، تولید و انتقال توان در سیستم‌های قدرت است. سیستم‌های سه‌فاز، ممکن است متعادل یا نامتعادل باشند. اگر سیستم متعادل باشد، با یکی از فازها می‌توان آن را تحلیل کرد. اما اگر سیستم نامتعادل باشد، تحلیل مدار کمی پیچیده‌تر است. در این آموزش، سیستم‌های سه‌فاز متعادل را معرفی، و روابط مربوط به آن‌ها را بیان می‌کنیم.

تولید ولتاژ‌ سه‌فاز

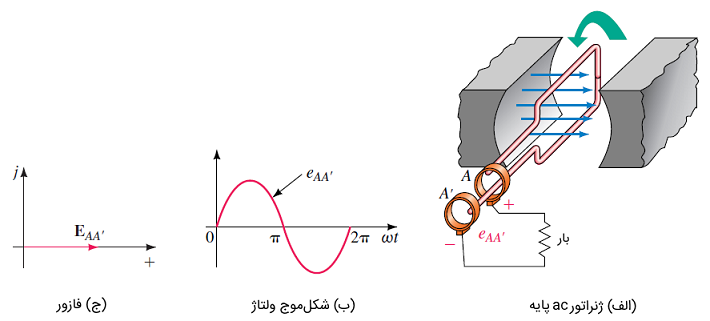
ژنراتورهای سه‌فاز، سه مجموعه سیم‌پیچی دارند و به همین دلیل سه ولتاژ ac را تولید می‌کنند. برای درک چگونگی این موضوع، ابتدا ژنراتور ساده تک‌فاز شکل ۱ را در نظر بگیرید. وقتی حلقه سیم‌پیچ $$AA'$$ می‌چرخد، شکل‌موج سینوسی $$e_{AA'}$$ را مطابق شکل ۱ (ب) تولید می‌کند.

فیلم آموزش مدارهای الکتریکی ۱ – جامع و کاربردی در فرادرس

کلیک کنید

این ولتاژ را می‌توان با فازور $$\mathbf{E}_{AA'}$$ شکل ۱ (ج) نشان داد.

اگر دو سیم‌پیچ دیگر به شکل ۱ اضافه کنیم، دو ولتاژ دیگر نیز تولید می‌شود (شکل ۲). از آن جایی که این سیم پیچ‌ها مشابه $$AA'$$ هستند (تفاوت آن‌ها فقط در موقعیت روی رتور است)، ولتاژهای یکسانی تولید می‌کنند. هرچند، چون سیم‌پیچ $$BB'$$ به‌اندازه $$120 ^ \circ$$ عقب‌تر از سیم‌پیچ $$AA'$$ است، ولتاژ $$\mathbf{e}_{BB'}$$ به‌اندازه $$120 ^ \circ$$ از $$\mathbf{e}_{AA'}$$ عقب‌تر خواهد بود. به‌طریق مشابه، سیم‌پیچ $$CC'$$ که $$120 ^ \circ$$ جلو‌تر از سیم‌پیچ $$AA'$$ است، ولتاژ $$\mathbf{e}_{CC'}$$ را تولید می‌کند که به‌اندازه $$120 ^ \circ$$ پیش‌فاز است. شکل‌موج‌ها در شکل ۲ (ب)، و فازورها در شکل ۲ (ج) نشان داده شده‌اند. همان‌گونه که مشخص است، اندازه ولتاژها برابر است و زاویه آن‌ها به اندازه $$120 ^ \circ$$‌ با هم تفاوت دارد.

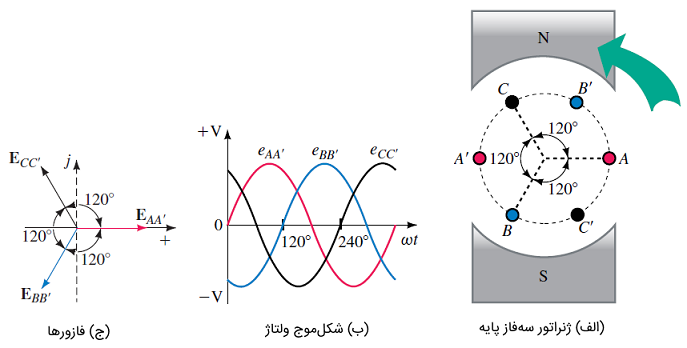
بنابراین، اگر فرض کنیم $$\mathbf{E}_{AA^ \prime}$$ در زاویه فاز $$0^ \circ$$ قرار دارد، آن‌گاه $$\mathbf{E}_{BB^ \prime}$$ در $$-120^\circ$$ و $$\mathbf{E}_{CC^ \prime}$$ در $$+120 ^ \circ$$ خواهند بود. اگر فرض کنیم مقدار rms ولتاژ $$120\, \mathrm{V}$$ باشد و مرجع $$0^\circ$$ را برای فازور $$\mathbf{E}_{AA^ \prime}$$ در نظر بگیریم، دنباله ولتاژهای $$\mathbf{E}_{BB^ \prime}\, \angle 0^ \circ$$، $$\mathbf{E}_{AA^ \prime}\, \angle -120^ \circ$$ و $$\mathbf{E}_{CC^ \prime}\, \angle 120^ \circ$$ را داریم. چنین مجموعه‌ای از ولتاژها را متعادل می‌گوییم. به‌دلیل وجود رابطه مشخص بین ولتاژهای متعادل، می‌توان با داشتن یکی از آن‌ها، دو ولتاژ دیگر را به‌سادگی تعیین کرد.

اتصالات اساسی مدار سه فاز

منبع شکل ۲، سه سیم‌پیچ مستقل $$AA^\prime$$ ،$$BB^\prime$$ و $$CC^\prime$$ دارد. در ابتدا شاید بارها را با شش سیم به منابع ولتاژ متصل کنیم (شکل 3 (الف)). این کار، شدنی است، اما چیزی نیست که در عمل انجام می‌شود (البته می‌توان از مفهوم آن استفاده کرد).

فیلم آموزش مدارهای الکتریکی 1 – مرور و حل تست در فرادرس

کلیک کنید

برای درک بهتر این موضوع، فرض کنید ولتاژ $$120$$ ولتی سیم‌پیچ، به یک بار مقاومتی $$12$$ اهمی وصل است. با در نظر گرفتن $$\mathbf{E}_{AA^ \prime}$$ به‌عنوان مرجع، قانون اهم را به مدار اعمال کرده و جریان‌ها را به‌صورت زیر به‌دست می‌آوریم:

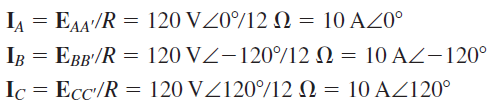
جریان‌های فوق، مطابق شکل ۳ (ب)، یک مجموعه متعادل را تشکیل می‌دهند.

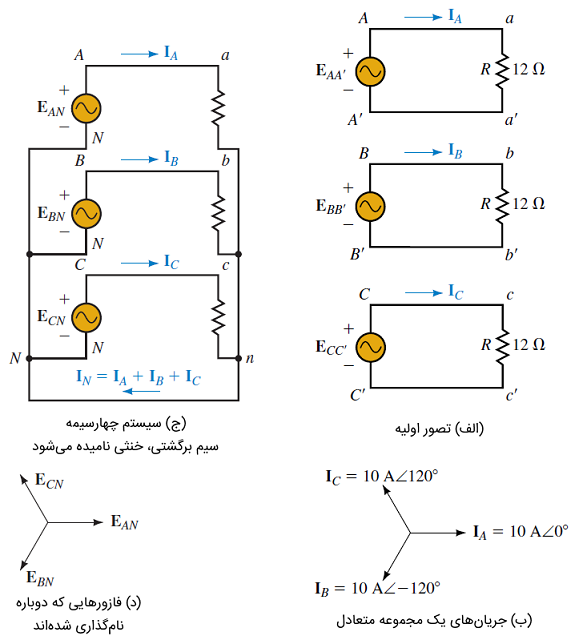
سیستم‌های چهارسیمه و سه‌سیمه

در شکل ۳ (الف)، هر بار، مدار بازگشت جریان مربوط به خود را دارد. اگر این مدارها را با مدار شکل ۳ (ج) جایگزین کنیم چه اتفاقی می‌افتد؟ با استفاده از قانون جریان کیرشهف (KCL)، جریان سیمی که «خنثی» (Neutral) نامیده می‌شود، برابر با جمع فازوری سه جریان $$\mathbf{I}_A$$، $$\mathbf{I}_B$$ و $$\mathbf{I}_C$$ است. برای سیستم شامل بار $$12$$ اهمی، داریم:

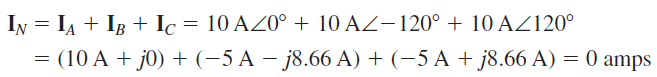
بنابراین، سیم برگشت، جریانی ندارد. این نتیجه در سیستم‌های متعادل (یعنی با بارهای یکسان)،‌ بدون توجه به امپدانس بار همواره درست است. در عمل، سیستم‌های قدرت تقریباً متعادل هستند. بنابراین،‌ جریان برگشتی نزدیک صفر است و البته لزوماً صفر نیست. به همین دلیل می‌توان سطح مقطع سیم خنثی را نسبت به سایر سیم‌ها کوچک‌تر انتخاب کرد. این پیکربندی، سیستم چهارسیمه (Four-wire system) نامیده می‌شود و یکی از پیکربندی‌هایی است که در عمل مورد استفاده قرار می‌گیرد.

خطوط شکل ۳ (الف)، هادی‌های خط یا فاز نامیده می‌شوند. احتمالاً این هادی‌ها را در خطوط انتقال یا توزیع دیده‌اید.

نمادگذاری

نقاط اتصال $$a$$، $$b$$ و $$c$$ شکل 3 (ج) را با $$A^ \prime$$، $$B^ \prime$$ و $$C^ \prime$$ نشان می‌دهیم و برای سادگی با نقطه مشترک $$N$$ نشان می‌دهیم. بنابراین، ولتاژها با نام‌های $$\mathbf{E}_{AN}$$، $$\mathbf{E}_{BN}$$ و $$\mathbf{E}_{CN}$$ مطابق شکل ۳ (د) نشان می‌دهیم . این ولتاژها به‌نام ولتاژهای خط به خنثی شناخته می‌شوند.

نمایش استاندارد

مدارهای سه‌فاز را معمولاً مطابق آن‌چه در شکل ۳ (الف) و (ج) نشان داده شده است، نمایش نمی‌دهند. برای نمایش سیم‌پیچ ژنراتور از نماد سلف و نیز دایره برای منبع ولتاژ آن استفاده می‌شود.

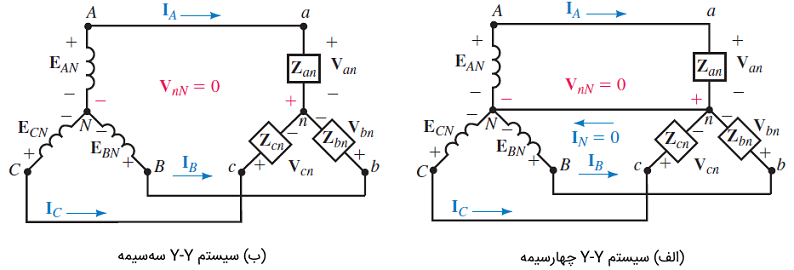
همان‌گونه که از شکل ۴ (الف) مشخص است، یک مدار Y-Y یا ستاره-ستاره داریم که به‌عنوان یک سیستم Y-Y چهارسیمه شناخته می‌شود. با کمی تغییر می‌توان مطابق شکل ۴ (ب) به یک سیستم Y-Y سه‌سیمه رسید.

هنگامی می‌توان از مدارهای Y-Y سه‌سیمه استفاده کرد که تضمین شود سیستم متعادل باقی می‌ماند، زیرا در شرایط تعادل، از هادی خنثی جریانی نمی‌گذرد. در عمل، سیستم‌های Y-Y اغلب چهارسیمه هستند.

ژنراتورهای با اتصال دلتا یا مثلث

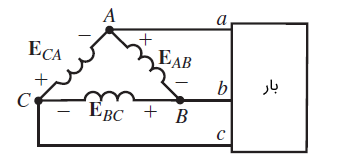
اکنون ژنراتورهایی را بررسی می‌کنیم که اتصال سیم‌پیچ آن‌ها به‌صورت $$\Delta$$ یا مثلث است. از نظر تئوری، این کار مطابق شکل ۵ انجام خواهد شد. هرچند در عمل، دشواری‌هایی وجود دارد. برای مثال،‌ وقتی بار به ژنراتور وصل شود، به‌دلیل شار مغناطیسی ناشی از جریان بار، در ولتاژ سیم‌پیچ‌ها اعوجاج رخ می‌دهد.

$$\Delta$$" width="343" height="167">

در اتصال ستاره، اعوجاج‌ها حذف می‌شوند، اما در اتصال مثلث باقی می‌مانند. اعوجاج باعث تولید هارمونیک سوم جریان می‌شود که در سیم‌پیچ‌های ژنراتور با اتصال $$\Delta$$ گردش می‌کند، درنتیجه، بازده کاهش می‌یابد. به این دلیل و دلایل دیگر، ژنراتورهایی که اتصال سیم‌پیچ آن‌ها به‌صورت $$\Delta$$ است، به‌ندرت در سیستم‌های قدرت مورد استفاده قرار می‌گیرند. به همین دلیل، در این آموزش، این سیستم‌ها را بررسی نمی‌کنیم.

ولتاژ خنثی به خنثی در یک مدار Y-Y

در یک سیستم Y-Y متعادل، جریان خنثی صفر است، زیرا مجموع جریان‌های خطوط، صفر است. در نتیجه، ولتاژ بین نقاط خنثی صفر است. برای دیدن دلیل این گفته، دوباره شکل ۴ (الف) را ببینید. فرض کنید امپدانس سیم رابط بین دو نقطه $$N$$ و $$n$$ برابر با $$\mathbf{Z}_{nN}$$ باشد. در نتیجه، ولتاژ‌ برابر است با $$\mathbf{V}_{nN}= \mathbf{I}_N \times \mathbf{Z}_{nN}$$. اما از آن‌جایی که $$\mathbf{I}_N=0$$ است، $$\mathbf{V}_{nN}=0$$ خواهد بود (بدون توجه به مقدار $$\mathbf{Z}_{nN}$$). حتی اگر هادی خنثی در شکل ۴ (ب) وجود نداشته باشد، مقدار $$\mathbf{V}_{nN}$$ هم‌چنان صفر باقی می‌ماند. بنابراین، در یک سیستم Y-Y متعادل، ولتاژ بین نقاط خنثی، صفر است.

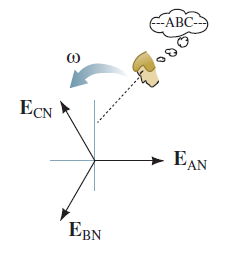
دنباله فاز

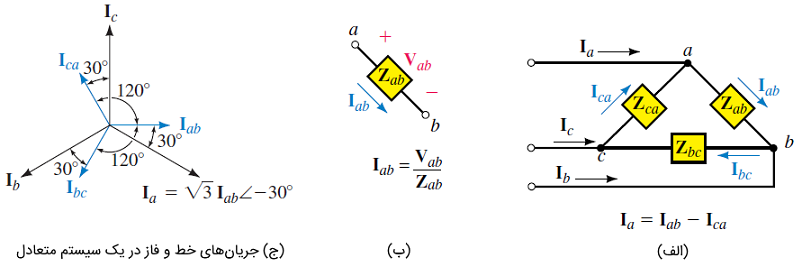
دنباله فاز، به ترتیبِ ولتاژهای سه‌فاز گفته می‌شود. این موضوع را می‌توان در قالب فازورها بررسی کرد. اگر (از نظر مفهومی) به چرخش فازور مجموعه شکل ۶ نگاه کنیم، برای مثال، می‌بینیم که فازورها با ترتیب $$\ldots ABCABC \ldots$$ می‌چرخند. این دنباله را دنباله فاز ABC یا دنباله فاز مثبت می‌نامیم. از سوی دیگر، اگر جهت چرخش را عکس کنیم، دنباله به‌صورت $$ACB$$ خواهد بود (دنباله فاز منفی). از آن‌جایی که سیستم‌های قدرت، دنباله $$ABC$$ را تولید می‌کنند (شکل ۲)، فقط این دنباله را بررسی می‌کنیم. در حالی که ولتاژها در دنباله $$ABC$$ تولید می‌شوند، ترتیب ولتاژهای اعمالی به بار، به نحوه اتصال آن به منبع بستگی دارد. برای بسیاری از بارهای متعادل، دنباله فاز اهمیتی ندارد. البته، ترتیب فاز در موتورهای سه‌فاز مهم است، زیرا اگر هر یک جفت سیم را با هم تعویض کنیم، جهت چرخش موتور تغییر خواهد کرد.

روابط اساسی مدارهای سه‌فاز

در این بخش، روابط اساسی ولتاژ و جریان مربوط به مدارهای سه‌فاز با اتصال ستاره و مثلث را بیان خواهیم کرد.

فیلم آموزش مدارهای الکتریکی ۲ – جامع و کاربردی در فرادرس

کلیک کنید

تعاریف

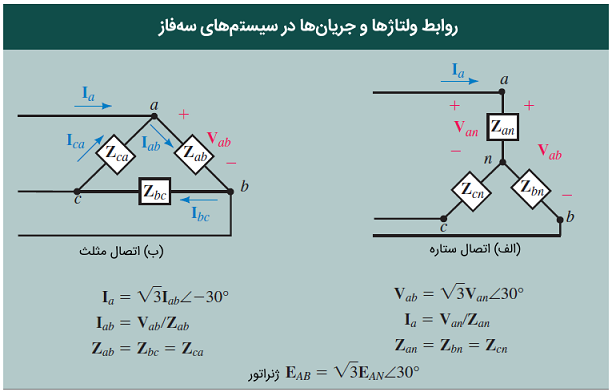
ولتاژهای خط (که خط به خط نیز نامیده می‌شود)، ولتاژ‌ بین خطوط هستند. بنابراین، $$\mathbf{E}_{AB}$$، $$\mathbf{E}_{BC}$$ و $$\mathbf{E}_{CA}$$ ولتاژهای خط به خط ژنراتور و $$\mathbf{V}_{ab}$$، $$\mathbf{V}_{bc}$$ و $$\mathbf{V}_{ca}$$ ولتاژهای خط به خط بار هستند.

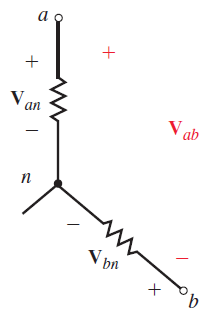
ولتاژهای فاز، ولتاژ فازها هستند. در یک بار Y، ولتاژ فاز، به‌عنوان اختلاف ولتاژ خط تا خنثی تعریف می‌شود (شکل ۷ (الف)). بنابراین، $$\mathbf{V}_{an}$$، $$\mathbf{V}_{bn}$$ و $$\mathbf{V}_{cn}$$ ولتاژهای فاز یک بار Y هستند. برای بار $$\Delta$$، فازها مطابق شکل ۷ (ب)، به‌صورت خط به خط بیان می‌شوند. همان‌طور که می‌بینیم، ولتاژهای فاز و خط در یک بار $$\Delta$$ مشابه هستند. برای ژنراتور شکل ۷ (الف)، مقادیر $$\mathbf{E}_{BN}$$، $$\mathbf{E}_{AN}$$ و $$\mathbf{E}_{CN}$$ ولتاژ فاز هستند.

جریان‌های خط، جریان‌هایی هستند که در هادی‌های خط می‌گذرند. برای نمایش این جریان، فقط از یک اندیس استفاده می‌کنیم. بنابراین، می‌توانیم از نمادهای $$\mathbf{I}_a$$، $$\mathbf{I}_b$$ و $$\mathbf{I}_c$$ در شکل ۷ یا $$\mathbf{I}_{A}$$، $$\mathbf{I}_{B}$$ و $$\mathbf{I}_{C}$$ در شکل ۴ استفاده کنیم. (البته گاهی از نمادهایی با دو اندیس نیز استفاده شده است، مانند $$\mathbf{I}_{Aa}$$)

جریان‌های فاز، جریان‌هایی هستند که از فازها عبور می‌کنند. برای بار Y شکل ۷ (الف)، جریان‌های $$\mathbf{I}_a$$، $$\mathbf{I}_b$$ و $$\mathbf{I}_c$$ از امپدانس‌های فاز می‌گذرند و به همین دلیل، جریان فاز هستند.

امپدانس‌های فاز یک بار Y، امپدانس‌های بین $$a-n$$، $$b-n$$ و $$c-n$$ هستند (شکل ۷ (الف)) و با نمادهای $$\mathbf{Z}_{an}$$، $$\mathbf{Z}_{bn}$$ و $$\mathbf{Z}_{cn}$$ نمایش داده می‌شوند. برای یک بار $$\Delta$$ (شکل ۷ (ب))، امپدانس‌های فاز، $$\mathbf{Z}_{ab}$$، $$\mathbf{Z}_{bc}$$ و $$\mathbf{Z}_{ca}$$ هستند. در یک بار متعادل، امپدانس همه بارها با هم برابر است.

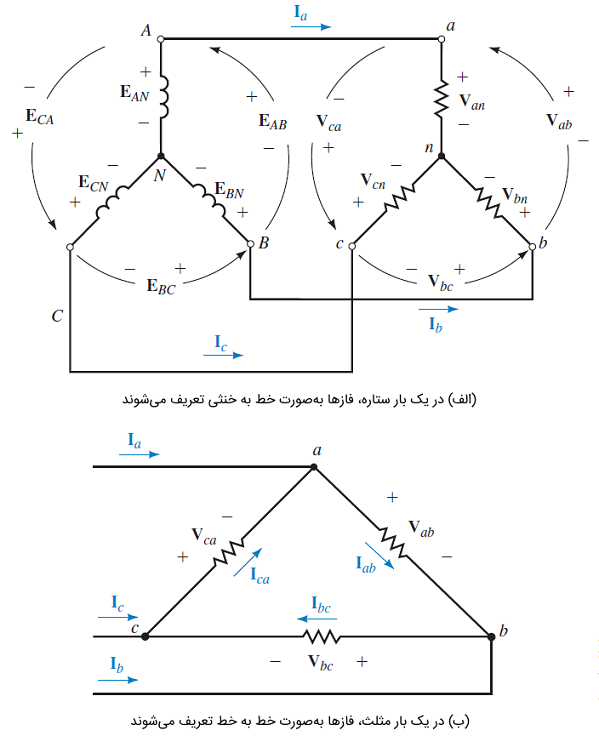
ولتاژ خط و فاز در یک مدار Y

در این قسمت، می‌خواهیم رابطه بین ولتاژ فاز و خط را در یک مدار ستاره پیدا کنیم. بدین منظور، شکل ۸ را در نظر بگیرید.

با اعمال KVL، داریم: $$\mathbf{V}_{ab}-\mathbf{V}_{an}+\mathbf{V}_{bn}=0$$. بنابراین:

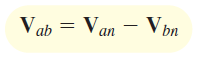
اکنون فرض کنید بزرگی هر یک از ولتاژها $$V$$ باشد و $$\mathbf{V}_{an}$$ را به‌عنوان مرجع در نظر بگیریم. بنابراین، $$\mathbf{V}_{an}=V \angle 0 ^ \circ$$ و $$\mathbf{V}_{bn}=V \angle -120 ^ \circ$$. با جایگذاری این دو مقدار در رابطه (۱)، داریم:

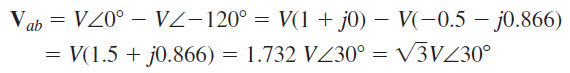
از طرفی می‌دانیم که $$\mathbf{V}_{an}=V \angle 0^ \circ$$. در نتیجه، رابطه زیر بین ولتاژ خط و ولتاژ فاز برقرار است:

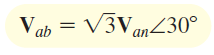
رابطه (۲) نشان می‌دهد که اندازه ولتاژ خط، $$\sqrt { 3 }$$ برابر اندازه ولتاژ فاز است. همچنین، زاویه ولتاژ خط، به‌اندازه $$30^\circ$$ از ولتاژ فاز جلوتر است. این موضوع، در شکل ۹ (الف) نشان داده شده است. برای دو فاز دیگر نیز روابط مشابه است (شکل 9 (ب)). بنابراین، برای منبع می‌توان نوشت:

ولتاژهای نامی

ولتاژ خط خروجی ترانسفورماتورهای توزیع برق، 400 ولت است. مشترکان خانگی، معمولاً ولتاژ تک‌فاز استفاده می‌کنند و با رابطه‌ای که بیان کردیم و عدد ۴۰۰ ولت خط، مقدار ولتاژ فاز حدوداً 230 ولت خواهد بود. این مقادیر را مقادیر نامی یا اسمی ولتاژ‌ می‌نامند که استفاده از آن‌ها متداول است. احتمالاً ولتاژ ۲۲۰ ولت را بیشتر از 230 ولت شنیده‌اید. هیچ‌کدام از این اعداد، اشتباه نیستند. ولتاژ ۲۳۰ ولت، مربوط به خروجی ترانسفورماتور است. به‌دلیلی تلفاتی که وجود دارد، این ولتاژ با اندازه حدود ۲۲۰ ولت به مصرف‌کننده می‌رسد.

با استفاده از معادلات (۲) و (۳)، می‌توان ولتاژ خط را با داشتن ولتاژ فاز محاسبه کرد:

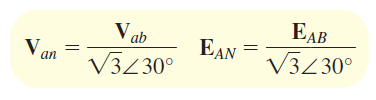
با بیان موارد فوق، اکنون این توانایی را داریم که با داشتن هریک از شش ولتاژ خط یا فاز، سایر ولتاژها را حساب کنیم. این کار به‌راحتی و با ضرب یا تقسیم اندازه بر $$\sqrt{3}$$ و جابه‌جایی زاویه به‌انداره $$30^\circ$$ انجام می‌شود.

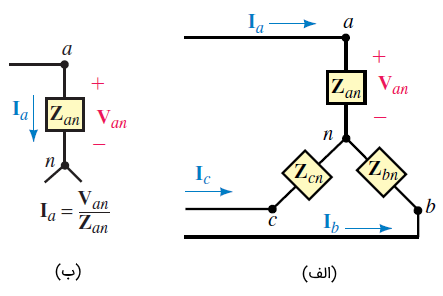
جریان در مدار ستاره

همان‌طور که دیدیم، جریان خط و فاز در یک بار ستاره، با هم برابر است. مطابق شکل 10 (ب)، داریم:

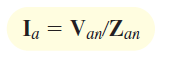
برای $$\mathbf{I}_b$$ و $$\mathbf{I}_c$$ نیز روابط مشابهی برقرار است. از آن‌جایی که $$\mathbf{V}_{bn}$$، $$\mathbf{V}_{an}$$ و $$\mathbf{V}_{cn}$$ یک مجموعه متعادل را تشکیل می‌دهند، جریان های خط V، $$\mathbf{I}_b$$ و $$\mathbf{I}_c$$ نیز یک مجموعه متعادل را شکل می‌دهند. بنابراین، با دانستن یکی از آن‌ها می‌توان دوتای دیگر را نیز به‌دست آورد.

جریان‌های خط و فاز یک مدار مثلث

بار مثلث شکل ۱1 را در نظر بگیرید. جریان فاز $$\mathbf{I}_{ab}$$ را می‌توان مطابق قسمت (ب) این شکل به‌دست آورد:

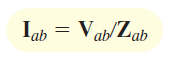
با روابط مشابه می‌توان جریان‌های $$\mathbf{I}_{bc}$$ و $$\mathbf{I}_{ca}$$ را نیز محاسبه کرد. از آن‌جایی که ولتاژ خطوط متعادل است، جریان‌های فاز نیز متعادل هستند. مجدداً شکل ۱1 (الف) را در نظر بگیرید. با اعمال KCL در گره $$a$$ داریم:

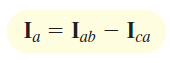
با کمی محاسبات جبری، می‌توان رابطه زیر را نوشت:

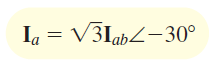
بنابراین، اندازه $$\mathbf{I}_a$$، برابر با $$\sqrt{3}$$ برابر $$\mathbf{I}_{ab}$$ است. همچنین، زاویه $$\mathbf{I}_a$$، به‌اندازه $$30 ^ \circ$$ از زاویه $$\mathbf{I}_{ab}$$ عقب‌تر است. این گفته برای دو فاز دیگر نیز صادق است. بنابراین، در یک مدار مثلث، اندازه جریان خط، $$\sqrt{3}$$ برابر اندازه اندازه جریان فاز است. همچنین، جریان هر خط، به‌اندازه $$30^\circ$$ از جریان فاز متناظر آن عقب‌‌تر است. از آن‌جایی که جریان‌های فاز، متعادل هستند، جریان‌های خط نیز متعادل خواهند بود. این موضوع، در شکل ۱1 (ج) نشان داده شده است. برای یافتن جریان‌های فاز با استفاده از جریان‌های خط، از رابطه زیر استفاده می‌کنیم:

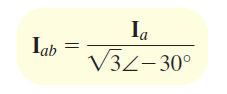
مدار معادل تک‌فاز

با توجه به نکاتی که گفتیم، واضح است اگر حل یک فاز سیستم سه‌فاز متعادل را داشته باشیم، می‌توانیم به‌سادگی کمیت‌های سه فاز دیگر را به‌دست آوریم. این گفته را می‌توان در قالب روش مدار معادل تک‌فاز برای سیستم‌های متعادل بیان کرد. یک سیستم Y-Y را با امپدانس خط در نظر بگیرید. سیستم ممکن است سه‌سیمه یا چهارسیمه با امپدانس هادی خنثی باشد. در هر دو حالت، از آن‌جایی که ولتاژ بین نقاط خنثی صفر است، می‌توان نقاط $$n$$ و $$N$$ را با یک هادی با امپدانس صفر به یک‌دیگر متصل کرد، بدون اینکه ولتاژ‌ یا جریان در هر جای مدار دچار تغییر شود. این موضوع، در شکل ۱2 (الف) نشان داده شده است.

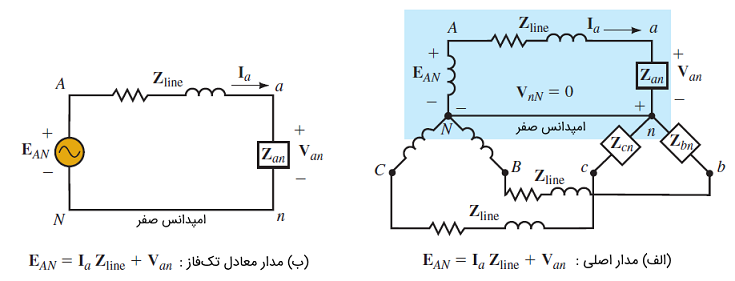
مطابق شکل 12 (ب)، می‌توان مدار فاز $$a$$ را جدا کرد. از آن‌جایی که $$V_{nN}=0$$ است، می‌توان گفت معادله‌ای که فاز $$a$$ در مدار شکل 12 (ب) را توصیف می‌کند، مشابه معادله‌ای است که در مدار اصلی وجود داشت. اگر بار $$\Delta$$ داشته باشیم،‌ آن را با استفاده از فرمول تبدیل $$\Delta - \mathrm{Y}$$ برای بارهای متعادل ($$\mathbf{Z}_\mathrm{Y}=\mathbf{Z}_\Delta /3$$) به بار Y تبدیل می‌کنیم. این کار را می‌توان بدون توجه به پیکربندی یا پیچیدگی مدار انجام داد، زیرا مدار متعادل است.

انتخاب مرجع

قبل از آنکه مدار سه‌فاز را حل کنیم، باید یک مرجع انتخاب کنیم. برای مدارهای Y، معمولاً $$\mathbf{E}_{AN}$$ یا $$\mathbf{V}_{an}$$ را به‌عنوان مرجع در نظر می‌گیریم. برای مدارهای $$\Delta$$ نیز، معمولاً $$\mathbf{E}_{AB}$$ یا $$\mathbf{V}_{ab}$$ را انتخاب می‌کنیم.

خلاصه روابط سه‌فاز اساسی

جدول زیر، خلاصه روابط اساسی در مدارهای سه‌فاز را نشان می‌دهد. لازم به ذکر است که در سیستم‌های متعادل (ستاره یا مثلث)، همه ولتاژها و همه جریان‌ها متعادل هستند.

در آموزش‌های بعدی، سایر مباحث مربوط به سیستم‌های سه‌فاز را بررسی خواهیم کرد.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• آموزش بررسی سیستم های قدرت 1
• سیستم پریونیت (Per-Unit) — از صفر تا صد
• پخش بار در سیستم قدرت — مفاهیم و معادلات

^^