یکی از کاربردهای مهم انتگرال سهگانه محاسبه حجم یک ناحیه است. بنابراین در این مطلب قصد داریم تا در قالب مثال نحوه محاسبه حجم با انتگرال سه گانه را توضیح دهیم.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
روش محاسبه حجم
در حالت کلی ناحیهای سهبعدی همچون U \large U U
V = ∭ U d x d y d z \large V = \iiint \limits_U { d x d y d z} V = U ∭ d x d y d z
این حجم را میتوان با استفاده از مختصات استوانهای، به صورت زیر نیز محاسبه کرد.
V = ∭ U ρ d ρ d φ d z \large V = \iiint \limits _ U { \rho d \rho d \varphi d z } V = U ∭ ρ d ρ d φ d z
به همین صورت رابطه محاسبه حجم در مختصات کروی به صورت زیر خواهد بود.
V = ∭ U ρ 2 sin θ d ρ d φ d θ \large V = \iiint \limits _ U { { \rho ^ 2 } \sin \theta d \rho d \varphi d \theta } V = U ∭ ρ 2 sin θ d ρ d φ d θ
در ادامه مثالهایی ارائه شده که در آنها این روشها توضیح داده شدهاند.
مثال ۱
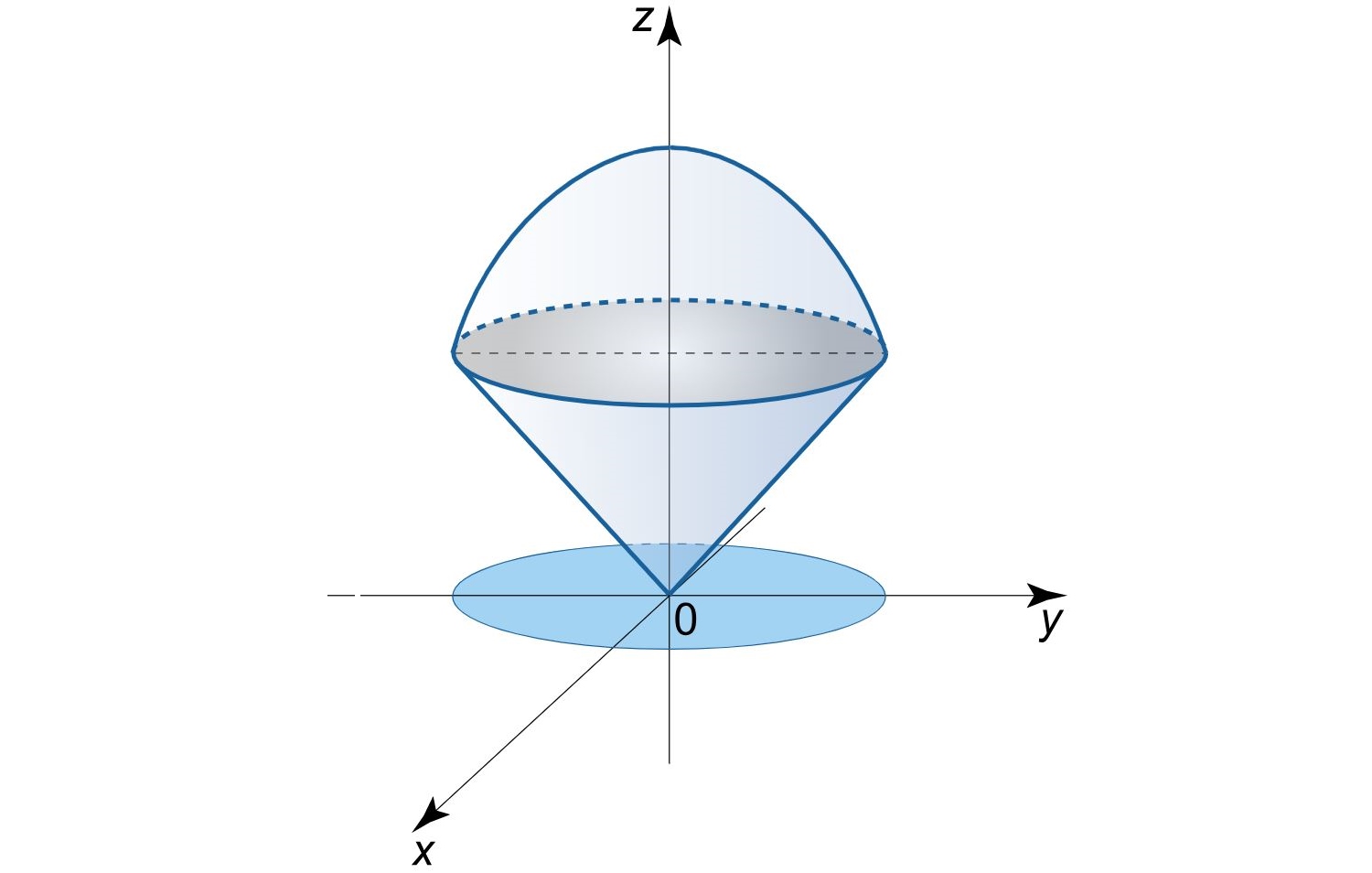
حجم مخروطی به ارتفاع H H H R R R
همانطور که در شکل زیر نیز میتوان دید، این مخروط توسط دو صفحه زیر محدود شدهاند.
z = H R x 2 + y 2 , z = H \large z = { \large \frac { H } { R} \normalsize} \sqrt { { x ^ 2 } + { y ^ 2 } } , z = H z = R H x 2 + y 2 , z = H
حجم ناحیه فوق را میتوان به صورت زیر محاسبه کرد.
V = ∭ U d x d y d z = ∫ – R R d x ∫ – R 2 – x 2 R 2 – x 2 d y ∫ H R x 2 + y 2 H d z \large {V = \iiint\limits_U {dxdydz} } = {\int\limits_{ – R } ^ R { d x } \int \limits _ { – \sqrt {{R^2} – { x ^ 2 } } } ^ { \sqrt { { R ^ 2 } – { x ^ 2 } } } { d y } \int \limits _ { \frac { H } { R } \sqrt {{ x ^ 2 } + { y ^ 2 } } } ^ H { d z } } V = U ∭ d x d y d z = – R ∫ R d x – R 2 – x 2 ∫ R 2 – x 2 d y R H x 2 + y 2 ∫ H d z
انتگرال فوق را میتوان در مختصات استوانهای و در بازههای زیر محاسبه کرد.
0 ≤ φ ≤ 2 π , 0 ≤ ρ ≤ R , ρ ≤ z ≤ H \large {0 \le \varphi \le 2\pi ,\;\;\;}\kern-0.3pt {0 \le \rho \le R \ \ , \ \ \;\;\;}\kern-0.3pt {\rho \le z \le H } 0 ≤ φ ≤ 2 π , 0 ≤ ρ ≤ R , ρ ≤ z ≤ H
عبارت انتگرالی بیان شده در بالا را میتوان در مختصات استوانهای به صورت زیر بیان کرد:
V = ∫ 0 R ρ d ρ ∫ 0 2 π d φ ∫ H R ρ H d z \large V = \int\limits_0^R {\rho d\rho } \int\limits_0^{2\pi } {d\varphi } \int\limits _ { \frac { H } { R } \rho } ^ H { d z } V = 0 ∫ R ρ d ρ 0 ∫ 2 π d φ R H ρ ∫ H d z
نهایتا حجم مخروط برابر خواهد بود با:
V = ∫ 0 R ρ d ρ ∫ 0 2 π d φ ∫ H R ρ H d z = 2 π ∫ 0 R ρ d ρ ∫ H R ρ H d z = 2 π ∫ 0 R ρ d ρ ⋅ [ z ∣ z = H R ρ z = H ] = 2 π ∫ 0 R ρ ( H – H R ρ ) d ρ = 2 π ∫ 0 R ( H ρ – H R ρ 2 ) d ρ = 2 π [ ( ρ 2 H 2 – ρ 3 H 3 R ) ∣ ρ = 0 ρ = R ] = 2 π ( R 2 H 2 – R 3 H 3 R ) = 2 π R 2 H 6 = π R 2 H 3 \large \begin {align*} V = & \int \limits _ 0 ^ R { \rho d \rho } \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int\limits_{\frac{H}{R}\rho }^H {dz} \\ & = {2\pi \int\limits_0^R {\rho d\rho } \int\limits_{\frac{H}{R}\rho }^H {dz} } \\ & = {2\pi \int\limits_0^R {\rho d\rho } \cdot \left[ {\left. z \right|_{z = \frac { H } { R } \rho } ^ { z = H } } \right] } \\ & = {2\pi \int\limits_0^R {\rho \left( {H – \frac { H } { R} \rho } \right)d\rho } } \\ & = {2\pi \int\limits_0^R {\left( {H\rho – \frac{H}{R}{\rho ^2}} \right)d\rho } } \\ & = {2\pi \left[ {\left. {\left( {\frac { { { \rho ^ 2 } H } } { 2 } – \frac{{{\rho ^3}H}}{{3R}}} \right)} \right|_{\rho = 0 } ^ { \rho = R}} \right] } \\ & = { 2 \pi \left( { \frac { { { R ^ 2 } H } } { 2 } – \frac { { { R ^ 3 } H } } { { 3 R } } } \right) } \\ & = { \frac { { 2 \pi { R ^ 2 } H } } { 6 } } \\ & = {\frac { { \pi { R ^ 2 } H }} { 3 } } \end {align*} V = 0 ∫ R ρ d ρ 0 ∫ 2 π d φ R H ρ ∫ H d z = 2 π 0 ∫ R ρ d ρ R H ρ ∫ H d z = 2 π 0 ∫ R ρ d ρ ⋅ [ z ∣ z = R H ρ z = H ] = 2 π 0 ∫ R ρ ( H – R H ρ ) d ρ = 2 π 0 ∫ R ( H ρ – R H ρ 2 ) d ρ = 2 π ( 2 ρ 2 H – 3 R ρ 3 H ) ρ = 0 ρ = R = 2 π ( 2 R 2 H – 3 R R 3 H ) = 6 2 π R 2 H = 3 π R 2 H
مثال ۲
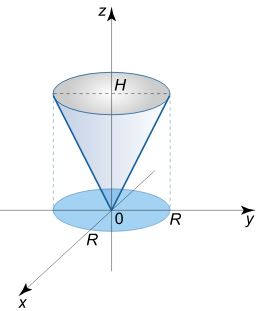
حجم چهار وجهی را بیابید که صفحات محدود کننده آن از نقاط A ( 1 , 0 , 0 ) , B ( 0 , 2 , 0 ) , C ( 0 , 0 , 3 ) A \left ( { 1 , 0 , 0 } \right ) , B ( 0 , 2 , 0 ) , C ( 0 , 0 , 3 ) A ( 1 , 0 , 0 ) , B ( 0 , 2 , 0 ) , C ( 0 , 0 , 3 )
با توجه به نقاط بیان شده، شکل ناحیه به صورت زیر خواهد بود.
معادله خط A B A B A B y = 2 – 2 x y = 2 – 2x y = 2–2 x x x x 0 ≤ x ≤ 1 0 \le x \le 1 0 ≤ x ≤ 1 y y y 0 ≤ y ≤ 2 – 2 x \large 0 \le y \le 2 – 2 x 0 ≤ y ≤ 2–2 x معادله صفحه نیز برابر است با:
x 1 + y 2 + z 3 = 1 \large \frac { x } { 1 } + \frac { y } { 2 } + \frac { z } { 3 } = 1 1 x + 2 y + 3 z = 1
در حالت کلی معادله صفحه A B C \large A B C A BC
6 x + 3 y + 2 z = 6 or z = 3 – 3 x – 3 2 y \large { 6 x + 3 y + 2 z = 6 \; \; \text{or} \; \; } \kern-0.3pt { z = 3 – 3 x – \frac { 3 } { 2 } y } 6 x + 3 y + 2 z = 6 or z = 3–3 x – 2 3 y
هدف از نوشتن معادله صفحه، بدست آوردن بازه z \large z z z \large z z
0 ≤ z ≤ 3 – 3 x – 3 2 y \large 0 \le z \le 3 – 3x – {\large\frac{3}{2}\normalsize} y 0 ≤ z ≤ 3–3 x – 2 3 y
نهایتا حاصل انتگرال برابر است با:
$$\large \require{cancel} \begin {align*}<br />
V & = \iiint\limits_U { d x d y d z }<br />
\\ & = {\int\limits_0^1 {dx} \int\limits_0^{2 – 2x} {dy} \int\limits_0^{3 – 3x – \frac{3}{2}y} {dz} }<br />
\\ & = {\int\limits_0^1 {dx} \int\limits_0^{2 – 2x} {dy} \cdot \left[ {\left. z \right|_0^{3 – 3x – \frac{3}{2}y}} \right] } = {\int\limits_0^1 {dx} \int\limits_0^{2 – 2x} {\left( {3 – 3x – \frac{3}{2}y} \right)dy} }<br />
\\ & = {\int\limits_0^1 {dx} \cdot}\kern0pt{ \Big[ {\left. {\left( {3y – 3xy – \frac{3}{4}{y^2}} \right)} \right|_{y = 0}^{y = 2 – 2x}} \Big] }<br />
\\ & = {\int\limits_0^1 {\Big[ {3\left( {2 – 2x} \right) – 3x\left( {2 – 2x} \right) }}-{{ \frac{3}{4}{{\left( {2 – 2x} \right)}^2}} \Big] dx} }<br />
\\ & = {\int\limits_0^1 {\Big[ {6 – 6x – 6x + 6{x^2} }}-{{ \frac{3}{4}\left( {4 – 8x + 4{x^2}} \right)} \Big] dx} }<br />
\\ & = {\int\limits_0^1 {\left( { { 6 } – { 12 x } +{6{x^2}} }\right.}-{\left.{ {3} + {6x} – {3{x^2}}} \right)dx} }<br />
\\ & = {3\int\limits_0^1 {\left( { {1} – { 2 x } + { x ^ 2 } } \right ) d x } }<br />
\\ & = {3\left[ {\left. {\left( {x – { x ^ 2 } + \frac { { { x ^ 3 } }} { 3 } } \right)} \right| _ 0 ^ 1 } \right] }<br />
\\ & = {3 \cdot \left ( { \cancel { 1 } – \cancel { 1 ^ 2 } + \frac { { { 1 ^ 3} } } { 3 } } \right ) } = { 1 } \end {align*} $$
مثال ۳
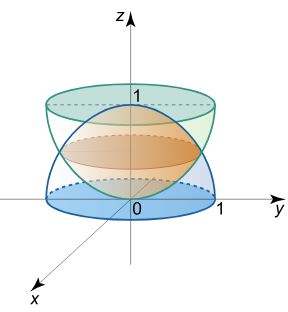
حجم ناحیه محصور بین دو سهمی گون زیر را بدست آورید.
z 1 = x 2 + y 2 , z 2 = 1 – x 2 – y 2 \large {{z_1} = {x^2} + { y ^ 2 } \; \; \ , \ \;\;}\kern-0.3pt { { z _ 2 } = 1 – { x ^ 2 } – { y ^ 2 } } z 1 = x 2 + y 2 , z 2 = 1– x 2 – y 2
این ناحیه به شکل زیر خواهد بود.
ناحیه فوق به صورت محیطی متقارن است. بنابراین با در نظر گرفتن ρ 2 = x 2 + y 2 \large { \rho ^ 2 } = { x ^ 2 } + { y ^ 2 } ρ 2 = x 2 + y 2
z 1 = ρ 2 , z 2 = 1 – ρ 2 \large { { z _ 1 } = { \rho ^ 2 } \; \; \ , \ \;\;}\kern-0.3pt { { z _ 2 } = 1 – { \rho ^ 2 } } z 1 = ρ 2 , z 2 = 1– ρ 2
با برابر قرار دادن رابطه دو سهمی، منحنی برخورد آنها به صورت زیر بدست خواهد آمد.
ρ 2 = 1 – ρ 2 ⇒ 2 ρ 2 = 1 ⇒ ρ 2 = 1 2 or z = 1 2 = 2 2 \large { { \rho ^ 2 } = 1 – {\rho ^2} \; \; } \Rightarrow { 2 { \rho ^ 2 } = 1 \; \; } \Rightarrow { { \rho ^ 2 } = \frac { 1 } { 2 } \; \; } \kern0pt {\text{or}\;\;z = \frac { 1 } { { \sqrt 2 } } = \frac { { \sqrt 2 } } { 2 } } ρ 2 = 1– ρ 2 ⇒ 2 ρ 2 = 1 ⇒ ρ 2 = 2 1 or z = 2 1 = 2 2
به ازای این مقدار از ρ \large \rho ρ z \large z z
z = ( 2 2 ) 2 = 1 2 \large z = { \left ( { \frac { { \sqrt 2 } } { 2 } } \right ) ^ 2 } = \frac { 1 } { 2 } z = ( 2 2 ) 2 = 2 1
با بدست آمدن ماکزیمم مقدار ρ \large \rho ρ
V = ∭ U d x d y d z = ∫ 0 2 π d φ ∫ 0 2 2 ρ d ρ ∫ ρ 2 1 – ρ 2 d z = ∫ 0 2 π d φ ∫ 0 2 2 ρ d ρ ⋅ [ z ∣ ρ 2 1 – ρ 2 ] = ∫ 0 2 π d φ ∫ 0 2 2 ρ ( 1 – ρ 2 – ρ 2 ) d ρ = 2 π ∫ 0 2 2 ( ρ – 2 ρ 3 ) d ρ = 2 π [ ( ρ 2 2 – 2 ρ 4 4 ) ∣ 0 2 2 ] = 2 π [ ( 2 2 ) 2 2 – ( 2 2 ) 4 2 ] = π ( 1 2 – 1 4 ) = π 4 \large \begin {align*} V = & \iiint \limits _ U { d x d y d z } \\ & = \int \limits _ 0 ^ { 2 \pi } { d \varphi \int \limits _ 0 ^ { \frac { { \sqrt 2 } } { 2 } } { \rho d \rho } \int \limits _ { { \rho ^ 2 } } ^ { 1 – { \rho ^ 2 } } { d z } } \\ & = { \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int\limits_0^{\frac{{\sqrt 2 }}{2}} {\rho d\rho } \cdot \left[ {\left. z \right|_{{\rho ^2}}^{1 – {\rho ^2}}} \right] } \\ & = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^{\frac{{\sqrt 2 }}{2}} {\rho \left( {1 – {\rho ^2} – {\rho ^2}} \right)d\rho } } \\ & = {2\pi \int\limits_0^{\frac{{\sqrt 2 }}{2}} {\left( {\rho – 2{\rho ^3}} \right)d\rho } } \\ & = { 2 \pi \left[ {\left. {\left( {\frac{{{\rho ^2}}}{2} – \frac { { 2 { \rho ^ 4 } } } {4 } } \right ) } \right|_0 ^ { \frac { { \sqrt 2 } }{ 2 } } } \right] } \\ & = {2\pi \left[ {\frac{{{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}}}{2} – \frac{{{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^4}}}{2}} \right] } \\ & = {\pi \left( {\frac{1}{2} – \frac{1}{4}} \right) } \\ & = {\frac{\pi }{4} } \end {align*} V = U ∭ d x d y d z = 0 ∫ 2 π d φ 0 ∫ 2 2 ρ d ρ ρ 2 ∫ 1– ρ 2 d z = 0 ∫ 2 π d φ 0 ∫ 2 2 ρ d ρ ⋅ [ z ∣ ρ 2 1– ρ 2 ] = 0 ∫ 2 π d φ 0 ∫ 2 2 ρ ( 1– ρ 2 – ρ 2 ) d ρ = 2 π 0 ∫ 2 2 ( ρ –2 ρ 3 ) d ρ = 2 π ( 2 ρ 2 – 4 2 ρ 4 ) 0 2 2 = 2 π 2 ( 2 2 ) 2 – 2 ( 2 2 ) 4 = π ( 2 1 – 4 1 ) = 4 π
مثال ۴
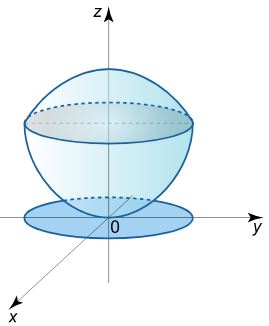
حجم ناحیه محصور شده به سهمیگون x 2 + y 2 = z \large { x ^ 2 } + { y ^ 2 } = z x 2 + y 2 = z x 2 + y 2 + z 2 = 6 \large { x ^ 2 } + { y ^ 2 } + { z ^ 2 } = 6 x 2 + y 2 + z 2 = 6
در ابتدا باید منحنی تقاطع این دو سطح را بدست آورد. بدین منظور داریم:
z + z 2 = 6 ⇒ z 2 + z – 6 = 0 ⇒ z 1 , 2 = – 1 ± 5 2 = 2 , – 3 \large { z + { z ^ 2 } = 6 \; \; } \Rightarrow { { z ^ 2 } + z – 6 = 0 \; \; } \Rightarrow { { z _ { 1 , 2 } } = \frac { { – 1 \pm 5 } } { 2 } = 2 , – 3 } z + z 2 = 6 ⇒ z 2 + z –6 = 0 ⇒ z 1 , 2 = 2 –1 ± 5 = 2 , –3
توجه داشته باشید که ریشه منفی نشان دهنده محل برخورد کره با سطح پایینی سهمیگون است؛ بنابراین آن را در نظر نمیگیریم. منحنی برخورد دو رویه و ناحیه مدنظر در شکل زیر نشان داده شده است.
همانطور که در بالا نیز شرح داده شد دو رویه در z = 2 \large z = 2 z = 2 دایره زیر قرار میگیرد.
x 2 + y 2 = 2 \large { x ^ 2 } + { y ^ 2 } = 2 x 2 + y 2 = 2
در بالای حجم مدنظر، کره و در زیر آن سهمی قرار گرفته است. بنابراین اندازه حجم را میتوان در مختصات کارتزینی به صورت زیر بیان کرد:
V = ∭ U d x d y d z = ∫ – 2 2 d x ∫ 0 2 – x 2 d y ∫ x 2 + y 2 6 – x 2 – y 2 d z \large {V = \iiint \limits _ U { d x d y d z } } = { \int \limits _ { – \sqrt 2 } ^ { \sqrt 2 } { d x } \int \limits _ 0 ^ {\sqrt {2 – {x^2}} } {dy} \int\limits _ { { x ^ 2 } + { y ^ 2 } } ^ { \sqrt { 6 – { x ^ 2 } – { y ^ 2 } } } { d z } } V = U ∭ d x d y d z = – 2 ∫ 2 d x 0 ∫ 2– x 2 d y x 2 + y 2 ∫ 6– x 2 – y 2 d z
با توجه به ناحیه انتگرالگیری، مناسب آن است که انتگرال را در مختصات استوانهای بنویسیم. بدین منظور انتگرال فوق را میتوان به صورت زیر بازنویسی کرد:
V = ∫ 0 2 π d φ ∫ 0 2 ρ d ρ ∫ ρ 2 6 – ρ 2 d z \large { V } = { \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int \limits _ 0 ^ { \sqrt 2 } { \rho d \rho } \int \limits _ { { \rho ^ 2 } } ^ { \sqrt { 6 – { \rho ^ 2 } } } { d z } } V = 0 ∫ 2 π d φ 0 ∫ 2 ρ d ρ ρ 2 ∫ 6– ρ 2 d z
توجه داشته باشید که در رابطه فوق، ρ \large \rho ρ ρ 2 = x 2 + y 2 \large {\rho ^2} = {x^2} + {y^2} ρ 2 = x 2 + y 2
V = ∫ 0 2 π d φ ∫ 0 2 ρ d ρ ∫ ρ 2 6 – ρ 2 d z = ∫ 0 2 π d φ ∫ 0 2 ρ d ρ ⋅ [ z ∣ ρ 2 6 – ρ 2 ] = ∫ 0 2 π d φ ∫ 0 2 ρ ( 6 – ρ 2 – ρ 2 ) d ρ = 2 π ∫ 0 2 ρ ( 6 – ρ 2 – ρ 2 ) d ρ = π ∫ 0 2 ( 6 – ρ 2 – ρ 2 ) d ρ 2 \large \begin {align*} V & = \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int \limits _ 0 ^ {\sqrt 2 } {\rho d\rho } \int\limits_{{\rho ^2}}^{\sqrt {6 – {\rho ^2}} } {dz} \\ & = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^{\sqrt 2 } {\rho d\rho } \cdot \left[ {\left. z \right|_{{\rho ^2}}^{\sqrt {6 – {\rho ^2}} }} \right] } \\ & = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^{\sqrt 2 } {\rho \left( {\sqrt {6 – {\rho ^2}} – {\rho ^2}} \right)d\rho } } \\ & = {2\pi \int\limits_0^{\sqrt 2 } {\rho \left( {\sqrt {6 – {\rho ^2}} – {\rho ^2}} \right)d\rho } } \\ & = {\pi \int\limits_0^{\sqrt 2 } {\left( {\sqrt {6 – {\rho ^2}} – {\rho ^2}} \right)d{\rho ^2}}} \end {align*} V = 0 ∫ 2 π d φ 0 ∫ 2 ρ d ρ ρ 2 ∫ 6– ρ 2 d z = 0 ∫ 2 π d φ 0 ∫ 2 ρ d ρ ⋅ [ z ∣ ρ 2 6– ρ 2 ] = 0 ∫ 2 π d φ 0 ∫ 2 ρ ( 6– ρ 2 – ρ 2 ) d ρ = 2 π 0 ∫ 2 ρ ( 6– ρ 2 – ρ 2 ) d ρ = π 0 ∫ 2 ( 6– ρ 2 – ρ 2 ) d ρ 2
نهایتا با استفاده از تغییر متغیر ρ 2 = t \large { \rho ^ 2 } = t ρ 2 = t
V = π ∫ 0 2 ( 6 – ρ 2 – ρ 2 ) d ρ 2 = π ∫ 0 2 ( 6 – t – t ) d t = π [ ( – 2 ( 6 – t ) 3 2 3 – t 2 2 ) ∣ 0 2 ] = π [ – 2 3 ( 4 3 2 – 6 3 2 ) – 2 ] = π [ 2 3 ( 6 6 – 8 ) – 2 ] = π ( 4 6 – 16 3 – 2 ) = 2 π ( 6 6 – 11 3 ) \large \begin {align*} {V }={ \pi \int\limits_0^{\sqrt 2 } {\left( {\sqrt {6 – {\rho ^2}} – {\rho ^2}} \right)d{\rho ^2}} } & = {\pi \int\limits_0^2 {\left( {\sqrt {6 – t} – t} \right)dt} } \\ & = {\pi \left[ {\left. {\left( { – \frac{{2{{\left( {6 – t} \right)}^{\large\frac{3}{2}\normalsize}}}}{3} – \frac{{{t^2}}}{2}} \right)} \right|_0^2} \right] } \\ & = {\pi \left[ { – \frac{2}{3}\left( {{4^{\large\frac{3}{2}\normalsize}} – {6^{\large\frac{3}{2}\normalsize}}} \right) – 2} \right] } \\ & = {\pi \left[ {\frac{2}{3}\left( {6\sqrt 6 – 8} \right) – 2} \right] } \\ & = {\pi \left( {4\sqrt 6 – \frac{{16}}{3} – 2} \right) } \\ & = {2\pi \left( {\frac{{6\sqrt 6 – 11}}{3}} \right) } \end {align*} V = π 0 ∫ 2 ( 6– ρ 2 – ρ 2 ) d ρ 2 = π 0 ∫ 2 ( 6– t – t ) d t = π – 3 2 ( 6– t ) 2 3 – 2 t 2 0 2 = π [ – 3 2 ( 4 2 3 – 6 2 3 ) –2 ] = π [ 3 2 ( 6 6 –8 ) –2 ] = π ( 4 6 – 3 16 –2 ) = 2 π ( 3 6 6 –11 )
فیلم های آموزش محاسبه حجم با انتگرال سه گانه – به زبان ساده (+ دانلود فیلم آموزش گام به گام) فیلم آموزشی محاسبه حجم با انتگرال سهگانه فیلم آموزشی حل چند مثال از محاسبه حجم با انتگرال سهگانه 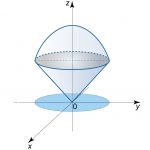













مثالها و فیلمها خیلی خوب بودن.ممنون