فیلتر کالمن — به زبان ساده

فیلتر کالمن (Kalman Filter) یک تخمین‌گر است که از تخمین حالت قبل و مشاهده فعلی برای محاسبه تخمین حالت فعلی استفاده می‌کند و یک ابزار بسیار قوی برای ترکیب اطلاعات در حضور نامعینی‌ها است. در برخی موارد، توانایی فیلتر کالمن برای استخراج اطلاعات دقیق خیره کننده است. فیلتر کالمن مدت‌هاست که به عنوان راه‌حل بهینه برای بسیاری از کارهای ردیابی و پیش‌بینی داده‌ها مورد استفاده قرار می‌گیرد.

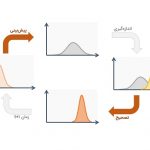
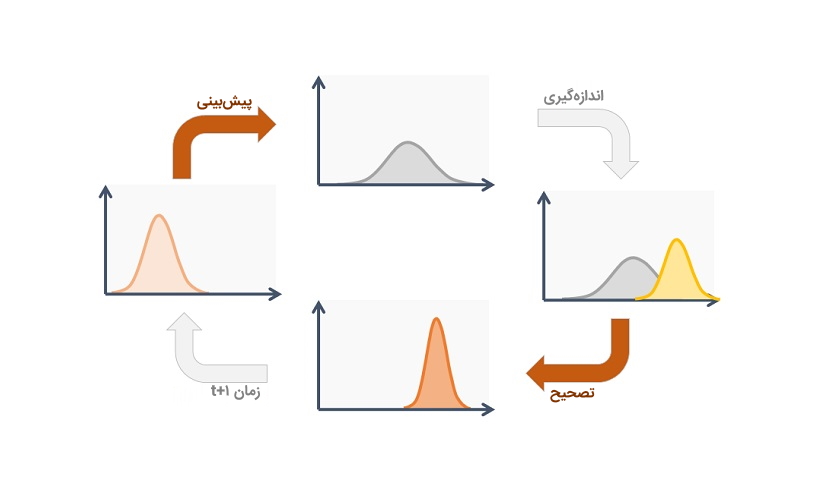
فیلتر کالمن چیست؟

هر جایی که اطلاعات نامعینی درباره یک سیستم دینامیکی داشته باشیم، می‌توانیم با استفاده از فیلتر کالمن تخمین مناسبی از تغییرات سیستم در آینده ارائه کنیم. فیلترهای کالمن برای سیستم‌هایی که مدام در حال تغییرند، ایده‌آل هستند. مزیت فیلترهای کالمن این است که به حافظه کمی نیاز دارند، زیرا به حافظه‌ای جز برای نگهداری اطلاعات وضعیت‌های قبلی نیاز ندارند. همچنین این فیلترها بسیار سریع هستند و به همین دلیل برای مسائل زمان حقیقی و سیستم‌های تعبیه‌ای مناسب هستند.

در نگاه اول، ظاهر ریاضیات مربوط به فیلتر کالمن، ترسناک و مبهم به نظر می‌رسد. اما کاملاً برعکس است و اگر به درستی برای یادگیری آن اقدام کنیم، فهم آن بسیار ساده خواهد بود. در این آموزش سعی می‌کنیم فیلتر کالمن را به صورت بصری و ساده شرح دهیم. برای یادگیری فیلتر کالمن، لازم است کمی درباره احتمال و ماتریس‌ها بدانیم.

با یک مثال ساده شروع می‌کنیم.

با یک فیلتر کالمن چه کاری می‌توانیم انجام دهیم؟

فرض کنید ربات کوچکی ساخته‌ایم که می‌تواند آزادانه در یک جنگل حرکت کند. این ربات برای آنکه مسیریابی کند، باید بداند دقیقاً در کجا قرار گرفته است.

وضعیت یا حالت (State) ربات را با $$\overrightarrow{x_k}$$ نشان می‌دهیم که شامل موقعیت (Position) و سرعت (Velocity) است:‌

$$\large \overrightarrow { x _ k } = ( \overrightarrow { p } , \overrightarrow { v } )$$

حالت یا بردار حالت، شامل اعدادی است که پیکربندی سیستم را نشان می‌دهند. در مورد این ربات، حالت شامل موقعیت و سرعت است. برای مثال، حالت یک سیستم می‌تواند اطلاعاتی درباره مقدار سیال یک مخزن، دمای موتور خودرو، موقعیت انگشت کاربر روی صفحه لمسی یا هر مورد دیگری باشد که ما بسته به نیاز، آن را در نظر می‌گیریم.

رباتی که درباره آن بحث کردیم، یک سنسور GPS با دقت تقریباً ۱۰ متر دارد که مقدار تقریباً مناسبی است. اما لازم است موقعیت ربات به صورت دقیق‌تر و کمتر از ۱۰ متر نیز در اختیار باشد، زیرا در جنگل صخره‌ها و گودال‌هایی وجود دارد و اگر ربات چند قدم اشتباه گام بردارد، ممکن است مثلاً درون گودالی بیفتد و دچار مشکل شود. بنابراین، وجود GPS به تنهایی برای مسیریابی ربات کافی نیست.

ممکن است چیزهای دیگری نیز درباره ربات بدانیم. مثلاً می‌دانیم فرمان‌هایی به موتور چرخ‌ها ارسال می‌شود و همچنین، اگر ربات در جهت خاصی حرکت کند و مشکلی برایش پیش نیاید، همان جهت حرکت قبلی را ادامه خواهد داد. اما اطلاعاتی درباره حرکت ربات در دست نیست؛ بنابراین، تعداد دور چرخ‌های ربات، نمی‌تواند دقیقاً تعیین کند که چه اندازه حرکت کرده است و در نتیجه، پیش‌بینی کامل نخواهد بود.

سنسور GPS اطلاعاتی را درباره حالت ربات به ما می‌دهد که البته غیرمستقیم بوده و اصطلاحاً نامعینی‌هایی دارد. پیش‌بینی ما نیز، اطلاعاتی را درباره چگونگی حرکت ربات به دست می‌دهد که غیرمستقیم بوده و با نایقینی یا نامعینی همراه است.

اما آیا اگر همه اطلاعات در دسترس استفاده کنیم، می‌توانیم پاسخ بهتری نسبت به تخمینی که خود اطلاعات ارائه می‌کنند داشته باشیم؟ قطعاً بله و این دقیقاً همان کاری است که فیلتر کالمن انجام می‌دهد.

مسئله از دیدگاه فیلتر کالمن چگونه است؟

حالت ساده‌ای را در نظر بگیرید که فقط از موقعیت و سرعت تشکیل شده است:

$$\large \overrightarrow { x } = \begin {bmatrix} p \\ v \end {bmatrix}$$

موقعیت و سرعت واقعی را نمی‌دانیم و طیف وسیعی از ترکیب‌های موقعیت و سرعت وجود دارند که می‌توانند درست باشند، اما تعدادی از آن‌ها نسبت به سایرین به واقعیت نزدیک‌ترند.

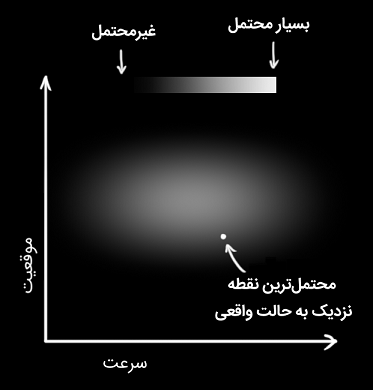
در فیلتر کالمن، فرض می‌شود که دو متغیر (در مثال ما، موقعیت و سرعت) تصادفی هستند و به صورت گوسی توزیع شده‌اند. هر متغیر یک مقدار میانگین (Mean) با نماد $$\mu$$ دارد که مرکز توزیع تصادفی (محتمل‌ترین حالت) است. متغیرها یک مقدار واریانس (Variance) با نماد $$\sigma ^ 2$$ نیز دارند که معرف نامعینی است. شکل زیر، این موضوع را به خوبی نشان می‌دهد.

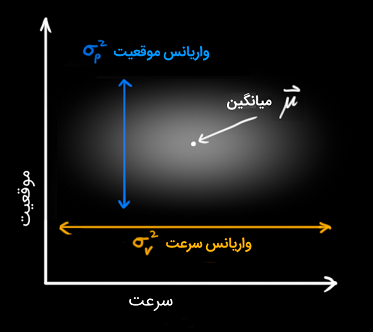
در شکل بالا، موقعیت و سرعت ناهمبسته (Uncorrelated) هستند. این بدین معنی است که وضعیت یک متغیر، اطلاعاتی درباره متغیر دیگر به دست نمی‌دهد.

شکل زیر، مورد جذاب‌تری را نشان می‌دهد که در آن، موقعیت و سرعت همبسته (Correlated) هستند. بنابراین، احتمال مشاهده یک موقعیت خاص به سرعت بستگی خواهد داشت.

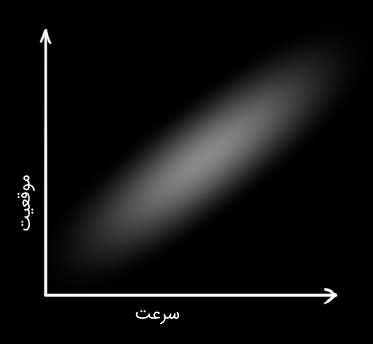
اگر برای مثال بخواهیم موقعیت جدید را بر اساس موقعیت قبلی تخمین بزنیم، این مورد (همبستگی) وجود خواهد داشت. اگر سرعت زیاد باشد، احتمالاً مسافت بیشتری پیموده می‌شود و در نتیجه، موقعیت دورتر خواهد بود. اگر به آرامی حرکت کنیم، به اندازه کمی دور خواهیم شد.

این رابطه بسیار مهم است، زیرا اطلاعات بیشتری به ما می‌دهد. به عبارت بهتر، یک اندازه‌گیری، اطلاعاتی را درباره سایر متغیرها ارائه می‌کند. هدف فیلتر کالمن نیز همین است که می‌خواهیم در حد امکان، اندازه‌گیری‌های نامعین را به عنوان اطلاعاتِ بیشتر، فشرده کنیم.

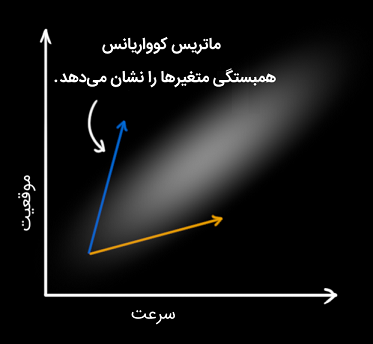
همبستگی را می‌توان در قالبی به نام ماتریس کوواریانس (Covariance Matrix) نشان داد. به طور خلاصه، هر درایه $$\Sigma_{ij}$$ از ماتریس کوواریانس، درجه همبستگی بین متغیر حالت $$i$$اُم و متغیر حالت $$j$$اُم را نشان می‌دهد. احتمالاً دریافته‌اید که به دلیل رابطه دوطرفه متغیرهای حالت، ماتریس کوواریانس متقارن (Symmetric) است. ماتریس کوواریانس را معمولاً با $$\mathbf{\Sigma}$$ و درایه‌های آن را با $$\Sigma_{ij}$$ نشان می‌دهند.

تعریف مسئله در قالب ماتریس‌ها

در این بخش، دانش خود درباره حالت را به عنوان یک حباب یا توده گوسی (Gaussian blob) مدل می‌کنیم.

بنابراین، به یک اطلاعات دوبخشی در زمان $$k$$ نیاز داریم. بهترین تخمین را $$\mathbf{\widehat{x}_k}$$ می‌نامیم (که همان میانگین $$\mu$$ است) و ماتریس کوواریانس $$\mathbf{P_k}$$‌ را به صورت زیر می‌نویسیم:

$$\large \begin {equation} \begin {aligned} \mathbf { \widehat { x } } _ k & = \begin {bmatrix} \text {position}\\ \text {velocity} \end {bmatrix} \\ \mathbf { P } _ k & = \begin {bmatrix} \Sigma _ { p p } & \Sigma _ { p v } \\ \Sigma _ { v p } & \Sigma _ { v v } \\ \end {bmatrix} \end {aligned} \end {equation} \;\;\;\;\; \;\; (1)$$

توجه کنید که در اینجا، فقط سرعت و موقعیت را در نظر گرفته‌ایم و بردار حالت می‌تواند هر تعداد متغیر حالت داشته باشد.

اکنون باید حالت فعلی (در زمان $$\color{royalblue}{{k-1}}$$) و پیش‌بینی حالت بعدی در زمان $$\color{deeppink}{k}$$ را تعیین کنیم. لازم به یادآوری است که اطلاعی نداریم کدام حالت واقعی است، اما این موضوع تأثیری در عملکرد پیش‌بینی ندارد؛ زیرا پیش‌بینی با همه آن‌ها کار می‌کند و توزیع جدیدی را نتیجه خواهد داد.

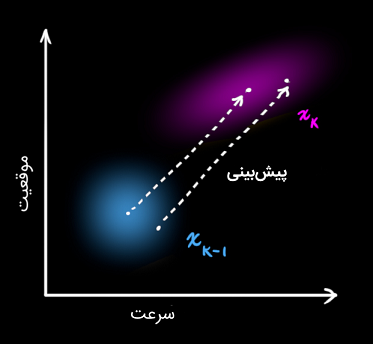
مرحله پیش‌بینی را با ماتریس $$\mathbf{F_k}$$ نمایش می‌دهیم.

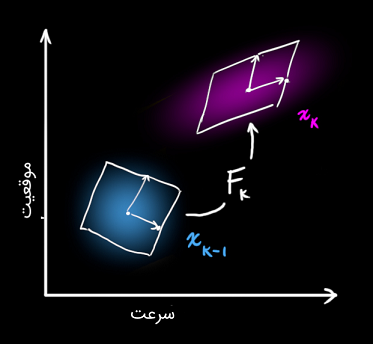
پیش‌بینی برای هر نقطه از تخمین اولیه (Original) انجام می‌شود و آن را به یک محل پیش‌بینی شده جدید انتقال می‌دهد.

اکنون بررسی می‌کنیم که چگونه باید از یک ماتریس برای پیش‌بینی موقعیت و سرعت در لحظه بعدی استفاده کنیم. از فرمول پایه‌ای سینماتیک زیر استفاده می‌کنیم:

$$ \large \begin {split}<br /> \color{deeppink} { p _ k } & = \color {royalblue} { p _ { k - 1 } } + \Delta t & \color {royalblue} { v _ { k - 1 } } \\<br /> \color {deeppink} { v _ k } & = & \color {royalblue} { v _ { k - 1 } }<br /> \end {split} $$

به عبارت دیگر:

$$\large \begin {align*} \color {deeppink} { \mathbf { \widehat { x } } _ k } & = \begin {bmatrix} 1 & \Delta t \\ 0 & 1 \end {bmatrix} \color {royalblue} { \mathbf { \widehat { x } } _ { k - 1 } } \;\;\;\;\;\;\; (2)\\ & = \mathbf { F } _ k \color {royalblue} { \mathbf { \widehat { x } } _ { k - 1 } } \;\;\;\;\;\;\; (3) \end {align*}$$

اکنون یک ماتریس پیش‌بینی داریم که حالت بعدی را به دست می‌دهد، اما هنوز نمی‌دانیم ماتریس کوواریانس را چگونه به‌روز کنیم.

حال به یک فرمول دیگر نیاز داریم. فکر می‌کنید اگر هر نقطه در توزیع را در یک ماتریس $$\color{firebrick}{\mathbf{A}}$$ ضرب کنیم، ماتریس کوواریانس $$\Sigma$$ چه تغییری خواهد کرد؟‌

ویژگی زیر را برای کوواریانس داریم:

$$\large \begin {align*} \begin {split} Cov ( x ) & = \Sigma \\ Cov ( \color {firebrick} { \mathbf { A } } x ) & = \color {firebrick} { \mathbf { A } } \Sigma \color {firebrick} { \mathbf { A } } ^ T \end {split} \end {align*} \;\;\;\;\;\;\; (4)$$

با ترکیب رابطه (۴) با (۳)، به فرمول‌های زیر می‌رسیم:

$$\large \begin {align*} \begin {split} \color {deeppink} { \mathbf { \widehat { x } } _ k } & = \mathbf { F } _ k \color {royalblue} { \mathbf { \widehat { x } } _ { k - 1} } \\ \color {deeppink} { \mathbf { P } _ k } & = \mathbf { F _ k } \color {royalblue} { \mathbf { P } _ { k - 1 } } \mathbf { F } _ k ^ T \end {split} \end {align*} \;\;\;\;\;\;\; (5)$$

اثر خارجی

گاهی ممکن است تغییراتی رخ دهد که مربوط به خود حالت نیست و محیط پیرامون است که بر سیستم اثر می‌گذارد.

برای مثال، اگر بردار حالت حرکت یک قطار را مدل کند، ممکن است اپراتور قطار با فشردن دکمه دریچه سوخت، سبب شتاب گرفتن آن شود. به طریق مشابه، در مثال رباتی بیان کردیم، نرم‌افزار مسیریابی ممکن است دستوری برای حرکت کردن یا ایستادن چرخ‌ها صادر کند. اگر این اطلاعات اضافه اعمال شده از خارج سیستم را بدانیم، می‌توانیم آن را با بردار $$\color{darkorange}{\overrightarrow{\mathbf{u}_k}}$$ نشان داده و به فرمول پیش‌بینی بیفزاییم.

فرض کنید شتاب مورد انتظار $$\color{darkorange}{a}$$ را در اثر تنظیم سوخت یا فرمان‌های کنترل می‌دانیم. از سینماتیک پایه می‌دانیم:

$$ \large \begin {split}<br /> \color {deeppink} { p _ k } & = \color {royalblue} { p _ { k - 1 } } + { \Delta t } & \color {royalblue} { v _{ k - 1 } } + & \frac { 1 } { 2 } \color {darkorange} { a } { \Delta t } ^ 2 \\<br /> \color {deeppink} { v _ k } & = & \color {royalblue} { v _ { k - 1 } } + & \color {darkorange} { a } { \Delta t }<br /> \end {split} $$

و به فرم ماتریسی، داریم:‌

$$\large \begin {align*} \begin {split} \color {deeppink} { \mathbf { \hat { x } } _ k } & = \mathbf { F } _ k \color {royalblue} { \mathbf { \hat { x } } _ { k -1 } } + \begin {bmatrix} \frac { \Delta t ^ 2 } { 2 } \\ \Delta t \end {bmatrix} \color {darkorange} { a } \\ & = \mathbf { F } _ k \color {royalblue} { \mathbf { \hat { x } } _ { k- 1 } } + \mathbf { B } _ k \color {darkorange} { \overrightarrow { \mathbf { u } _ k } } \end {split} \end {align*} \;\;\;\;\;\;\; (6)$$

در رابطه بالا، $$\mathbf{B}_k$$ ماتریس کنترل و $$\color{darkorange}{\overrightarrow{\mathbf{u}_k}}$$ بردار کنترل نامیده می‌شوند. در سیستم‌های ساده و بدون اثر خارجی، از این موارد چشم‌پوشی می‌کنیم.

اما اگر پیش‌بینی صددرصد دقیق نباشد چه‌کار باید کرد؟ در بخش بعدی به این پرسش پاسخ می‌دهیم.

نامعینی خارجی

فرض کردیم اثر خارجی که در بخش قبل درباره آن بحث کردیم، معلوم و شناخته شده است. اما اگر چیزی درباره اثرات خارج از سیستم ندانیم، چه باید کرد؟ اگر در حال مسیریابی یک کوادکوپتر باشیم،‌ برای مثال، باد می‌تواند آن را به هر سمتی ببرد. یا اگر یک ربات را مسیریابی کنیم، امکان دارد چرخ‌هایش دچار لغزش شده یا اصطکاک با سطح زمین روی آن اثر بگذارد. ما نمی‌توانیم این موارد را ردیابی کنیم و اگر هر کدام از این‌ها رخ دهد، ممکن است پیش‌بینی ما نتیجه اشتباهی داشته باشد.

راه‌حل این مشکل، مدل کردن نامعینی‌های دنیای پیرامون (هر چیزی که کنترلی روی آن نداریم) با اضافه کردن جمله‌ای به مرحله پیش‌بینی است:

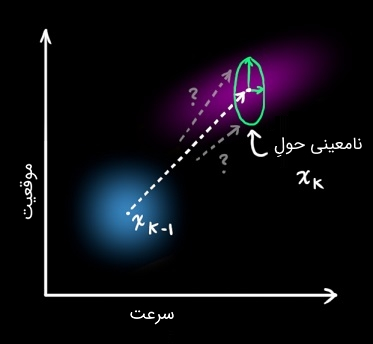
هر حالت در تخمین اولیه می‌تواند به محدوده‌ای از حالت‌ها حرکت کند. از آنجایی که یک حباب گوسی را در نظر گرفته‌ایم، می‌توان گفت که هر نقطه در $$\color{royalblue}{\mathbf{\hat{x}}_{k-1}}$$، به جایی در حباب گوسی با کوواریانس $$\color{mediumaquamarine}{\mathbf{Q}_k}$$ منتقل می‌شود. به بیان دیگر، تأثیرات ردیابی نشده را به عنوان نویزی با کوواریانس $$\color{mediumaquamarine}{\mathbf{Q}_k}$$ در نظر می‌گیریم.

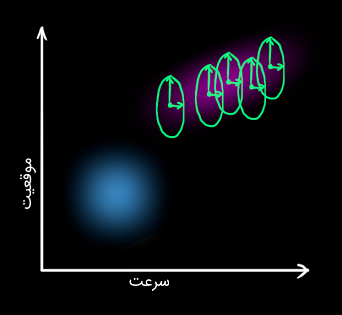
در نتیجه، یک حباب گوسی جدید خواهیم داشت که کواریانس متفاوتی نسبت به قبل دارد و البته میانگین آن تغییری نمی‌کند.

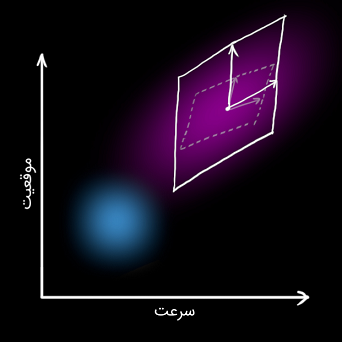
اکنون کوواریانسِ توسعه یافته به سادگی با افزودن $${\color{mediumaquamarine}{\mathbf{Q}_k}}$$ به دست می‌آید. در نتیجه، گام پیش‌بینی را می‌توان به صورت زیر نوشت:

$$\large \begin {equation} \begin {split} \color {deeppink} { \mathbf { \hat { x } } _ k } & = \mathbf { F } _ k \color {royalblue} { \mathbf { \hat { x } } _ { k - 1 } } + \mathbf { B } _ k \color {darkorange} { \overrightarrow { \mathbf { u } _ k } } \\ \color {deeppink} { \mathbf { P } _ k } & = \mathbf { F _ k } \color {royalblue} { \mathbf { P } _ { k - 1 } } \mathbf { F } _ k ^ T + \color {mediumaquamarine} { \mathbf { Q } _ k } \end {split} \end {equation} \; \; \; \; \; \; \; (7)$$

به بیان دیگر، بهترین تخمین جدید، یک پیش‌بینی است که از بهترین تخمین قبلی به اضافه یک تصحیح برای تأثیرات خارجی معلوم تشکیل شده است.

و نامعینی جدید، با افزودن نامعینی اضافه محیط به نامعینی قبلی پیش‌بینی می‌شود.

اکنون تخمینی از سیستم با $$\color{deeppink}{\mathbf{\hat{x}}_k}$$ و $$\color{deeppink}{\mathbf{P}_k}$$ داریم. حال اگر اطلاعاتی از سنسورها داشته باشیم، چه اتفاقی می‌تواند رخ دهد؟

تصحیح تخمین با اندازه‌گیری‌ها

گاهی ممکن است چند سنسور داشته باشیم که اطلاعاتی را درباره حالت سیستم به ما بدهند. ممکن است یک سنسور موقعیت و سنسور دیگر سرعت را اندازه بگیرد. هر سنسور اطلاعات غیرمستقیمی را درباره حالت به ما می‌دهد؛ به عبارت دیگر، سنسورها برای یک حالت به کار رفته و مجموعه‌ای از داده‌ها را تولید می‌کنند.

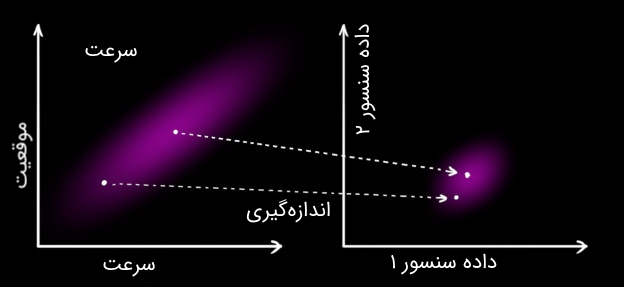
توجه کنید که واحدها و مقیاس داده‌های سنسورها ممکن است یکسان نباشد، زیرا واحد حالت‌های مختلف با هم تفاوت دارد. سنسورها را با ماتریس $$\mathbf{H}_k$$ مدل می‌کنیم.

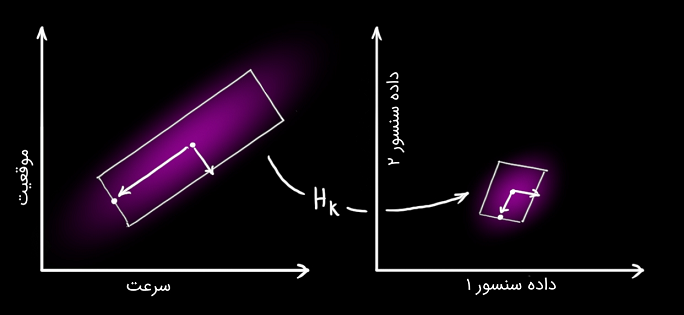
می‌توانیم توزیع داده‌های مورد انتظار سنسورها را به صورت زیر بنویسیم:

$$\large \begin {align*} \begin {aligned} \overrightarrow { \mu } _ { \text {expected} } & = \mathbf { H } _ k \color {deeppink} { \mathbf { \hat { x } } _ k } \\ \mathbf { \Sigma } _ { \text {expected} } & = \mathbf { H } _ k \color {deeppink} { \mathbf { P } _ k } \mathbf { H } _ k ^ T \end {aligned} \end {align*} \; \; \; \; \; \; \; (8)$$

یکی از ویژگی‌های بارز فیلتر کالمن همین مورد است که نویز سنسور را در نظر می‌گیرد. به عبارت دیگر، سنسورها حداقل تا حدی قابلیت اطمینان کمتر از ۱۰۰ درصد دارند و در نتیجه، ممکن است تخمین اولیه به بازه گسترده‌ای از داده سنسورها منجر شود.

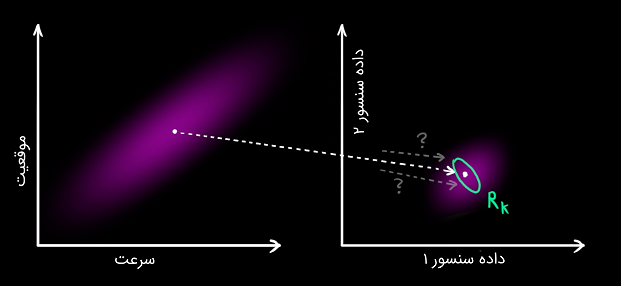
از هر داده‌ای که از سنسور مشاهده می‌کنیم، می‌توانیم حدس بزنیم که سیستم در یک حالت خاص بوده است. اما به دلیل آنکه نامعینی وجود دارد، برخی حالت‌ها محتمل‌تر از سایرین هستند:

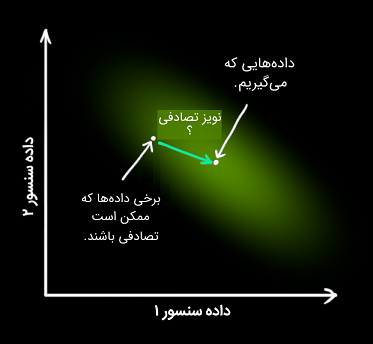
کواریانس این نامعینی (یعنی نویز سنسور) را $$\color{mediumaquamarine}{\mathbf{R}_k}$$ می‌نامیم. توزیع میانگینی برابر با داده‌ای دارد که از سنسور مشاهده کرده‌ایم و آن را $$\color{yellowgreen}{\overrightarrow{\mathbf{z}_k}}$$ می‌نامیم.

بنابراین، اکنون دو حباب گوسی داریم: یکی اطراف میانگین پیش‌بینیِ تبدیل شده و یکی اطراف داده سنسور واقعی.

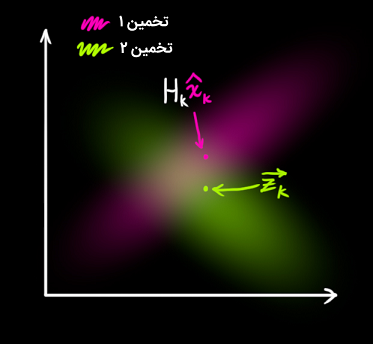
باید سعی کنیم حدسمان درباره داده سنسور را که بر اساس حالت پیش بینی شده (صورتی) دیده‌ایم با یک حدس متفاوت بر اساس قرائتمان از سنسور (سبز) که به صورت واقعی به دست آورده‌ایم، تطبیق دهیم.

اکنون محتمل‌ترین حالت کدام است؟ برای هر قرائت ممکن $$(z_1,z_2)$$، دو احتمال متناظر با آن وجود دارد: (۱) احتمال آنکه قرائت سنسور $$\color{yellowgreen}{\overrightarrow{\mathbf{z}_k}}$$ یک اندازه‌گیری اشتباه از $$(z_1,z_2)$$ باشد، و (۲) احتمال آنکه برای تخمین قبلی، $$(z_1 , z _ 2)$$ قرائتی است که باید ببینیم.

اگر دو احتمال داشته باشیم و بخواهیم شانس درست بودن هر دو را بدانیم، باید آن‌ها را در یکدیگر ضرب کنیم. بنابراین، هر دو توده گوسی را در هم ضرب می‌کنیم:

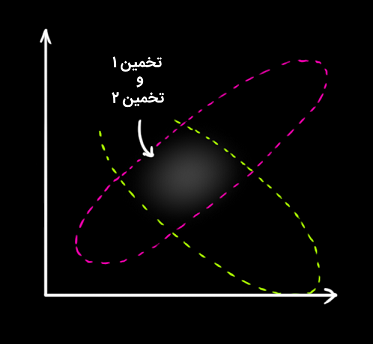
آنچه که باقی می‌ماند، همپوشانی ناحیه بین دو حباب است که درخشان‌تر نشان داده شده است و دقت بیشتری نسبت به تخمین‌های قبلی دارد. میانگین این توزیع نوعی پیکربندی است برای دو تخمینی که محتمل‌تر هستند و بنابراین، بهترین تخمین را از اطلاعاتِ در دسترس خواهیم داشت.

در نتیجه، یک حباب گوسی جدید خواهیم داشت:

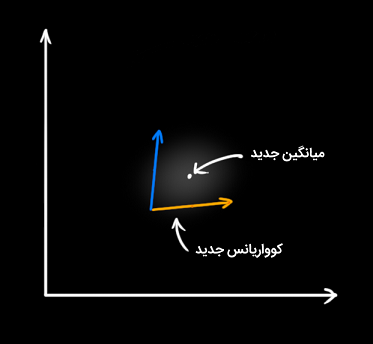
همان‌طور که گفتیم، وقتی دو حباب گوسی با میانگین‌ها و ماتریس‌های کوواریانس مجزا را در هم ضرب کنیم، یک حباب گوسی جدید با میانگین و ماتریس کواریانس مربوط به آن را داریم. بنابراین، باید فرمولی برای پارامترهای جدید با استفاده از پارامترهای قبلی داشته باشیم.

ترکیب گوسی‌ها

اکنون می‌خواهیم فرمولی را که راجع به آن صحبت کردیم پیدا کنیم. ساده‌ترین مورد، حالت یک‌بعدی است. یک زنگوله گوسی یک‌بعدی را با واریانس $$\sigma ^ 2$$ و میانگین $$\mu$$ در نظر بگیرید:

$$\large \begin {align*} \mathcal { N } ( x , \mu , \sigma ) = \frac { 1 } { \sigma \sqrt { 2 \pi } } e ^ { - \frac { (x – \mu ) ^ 2 } { 2 \sigma ^ 2 } } \end {align*} \; \; \; \; \; \; \; (9)$$

می‌‌خواهیم بدانیم با ضرب دو منحنی گوسی در یکدیگر چه اتفاقی می‌افتد. منحنی آبی شکل زیر اشتراک (نرمال نشده) بین دو توزیع گوسی را نشان می‌دهد.

$$\large \begin {align*} \mathcal { N } ( x , \color {fuchsia} { \mu _ 0 } , \color {deeppink} { \sigma _ 0 } ) \cdot \mathcal { N } ( x, \color {yellowgreen} { \mu _ 1 } , \color {mediumaquamarine}{ \sigma _ 1 } ) \stackrel { ? } { = } \mathcal { N } ( x , \color {royalblue} { \mu’ } , \color {mediumblue} { \sigma’ } ) \end {align*} \;\;\;\;\;\;\; (10)$$

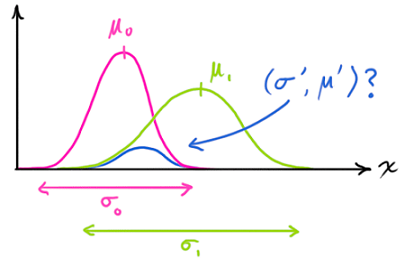
با جایگذاری معادله (۹) در معادله (۱۰) و مقداری عملیات جبری، احتمال کلی به دست می‌آید:

$$\large \begin {align*} \begin {aligned} \color {royalblue} { \mu’ } & = \mu _ 0 + \frac { \sigma _ 0 ^ 2 ( \mu _ 1 – \mu _ 0 ) } { \sigma _ 0 ^ 2 + \sigma _ 1 ^ 2 } \\ \color {mediumblue} { \sigma’ } ^ 2 & = \sigma _ 0 ^ 2 – \frac { \sigma _ 0 ^ 4 } { \sigma _ 0 ^ 2 + \sigma _ 1 ^ 2 } \end {aligned} \end {align*} \;\;\;\;\;\;\; (11)$$

با تعریف $$\color{purple}{\mathbf{k}}$$، فرمول‌های بالا را به صورت زیر می‌نویسیم:

$$\large \begin {align*} \color {purple} { \mathbf { k } } = \frac { \sigma _ 0 ^ 2 }{ \sigma _ 0 ^ 2 + \sigma _ 1 ^ 2 } \end {align*} \;\;\;\;\;\;\; (12)$$

$$ \large \begin {align*}<br /> \begin {split}<br /> \color {royalblue} { \mu’ } & = \mu _ 0 + & \color {purple} { \mathbf { k } } ( \mu _ 1 – \mu _ 0 ) \\<br /> \color {mediumblue} { \sigma’ } ^ 2 & = \sigma _ 0 ^ 2 – & \color {purple} { \mathbf { k } } \sigma _ 0 ^ 2<br /> \end {split}<br /> \end{align*} \; \; \; \; \; \; \; (13 )$$

اکنون مشاهده می‌کنید که چگونه می‌توان تخمین قبلی را گرفته و چیزی را به آن اضافه کنیم تا یک تخمین جدید ایجاد شود.

حال نسخه ماتریسی معادلات را می‌نویسیم. برای این کار، معادلات (۱۲) و (۱۳) را  به فرم ماتریسی می‌نویسیم. اگر $$\Sigma$$ ماتریس کوواریانس یک حباب گوسی و $$\overrightarrow { \mu}$$میانگین آن در طول هر محور باشد؛ بنابراین:

$$\large \begin {align*} \color {purple} { \mathbf { K } } = \Sigma _ 0 ( \Sigma _ 0 + \Sigma _ 1 ) ^ { - 1 } \end {align*} \;\;\;\;\;\;\; (14)$$

$$ \large \begin {align*}<br /> \begin {split}<br /> \color {royalblue} { \overrightarrow { \mu}’ } & = \overrightarrow { \mu _ 0 } + & \color {purple} { \mathbf { K } } ( \overrightarrow { \mu _ 1 } – \overrightarrow { \mu _ 0 } ) \\<br /> \color {mediumblue} { \Sigma’ } & = \Sigma _ 0 – & \color {purple} { \mathbf { K } } \Sigma _ 0<br /> \end {split}<br /> \end {align*} \;\;\;\;\;\;\; (15) $$

ترکیب همه موارد با هم

طبق مطالبی که گفتیم، دو توزیع داریم: اندازه‌گیری پیش‌بینی شده با $$(\color{fuchsia}{\mu_0}, \color{deeppink}{\Sigma_0}) = (\color{fuchsia}{\mathbf{H}_k \mathbf{\hat{x}}_k}, \color{deeppink}{\mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T})$$، و اندازه‌گیری مشاهده شده با $$(\color{yellowgreen}{\mu_1}, \color{mediumaquamarine}{\Sigma_1}) = (\color{yellowgreen}{\overrightarrow{\mathbf{z}_k}}, \color{mediumaquamarine}{\mathbf{R}_k})$$. می‌توان این اندازه‌گیری‌ها را در معادله (۱۵) قرار داد و همپوشانی آن‌ها را پیدا کرد:

$$\large \begin {align*} \begin {aligned} \mathbf { H } _ k \color {royalblue} { \mathbf { \hat { x } } _ k’ } & = \color {fuchsia} { \mathbf { H } _ k \mathbf { \hat { x } } _ k } & + & \color {purple} { \mathbf { K } } ( \color {yellowgreen} { \overrightarrow { \mathbf { z } _ k } } – \color {fuchsia}{ \mathbf { H } _ k \mathbf { \hat { x } } _ k } ) \\ \mathbf { H } _ k \color {royalblue} { \mathbf { P } _ k’ } \mathbf { H } _ k ^ T & = \color {deeppink} { \mathbf { H } _ k \mathbf { P } _ k \mathbf { H } _ k ^ T } & – & \color {purple} { \mathbf { K } } \color {deeppink} { \mathbf { H } _ k \mathbf { P }_ k \mathbf { H } _ k ^ T } \end {aligned} \end{align*} \;\;\;\;\;\;\; (16)$$

و از رابطه (۱۴)، بهره کالمن برابر است با:

$$\large \begin {align*} \color {purple} { \mathbf { K } } = \color {deeppink} { \mathbf { H } _ k \mathbf { P } _ k \mathbf { H } _ k ^ T } ( \color {deeppink} { \mathbf { H } _ k \mathbf { P } _ k \mathbf { H } _ k ^ T } + \color {mediumaquamarine} { \mathbf { R } _ k } ) ^ {- 1 } \end {align*} \;\;\;\;\;\;\; (17)$$

می‌توانیم $$\mathbf{H}_k$$  و $$\mathbf{H}_k^T$$ را با در نظر گرفتن ملاحظاتی حذف کرده و معادلات نهایی را به صورت زیر بنویسیم:

$$ \large \begin {align*}<br /> \begin {split}<br /> \color {royalblue} { \mathbf { \hat { x } } _ k’ } & = \color {fuchsia} { \mathbf { \hat { x } } _ k } & + & \color {purple}{ \mathbf { K }’ } ( \color {yellowgreen} { \overrightarrow { \mathbf { z } _ k } } – \color {fuchsia} { \mathbf { H } _ k \mathbf { \hat { x } } _ k } ) \\<br /> \color {royalblue} { \mathbf { P } _ k’ } & = \color {deeppink}{ \mathbf { P } _ k } & – & \color {purple} { \mathbf { K }’ } \color {deeppink} { \mathbf { H } _ k \mathbf { P } _ k }<br /> \end {split}<br /> \end {align*} \;\;\;\;\;\;\;\; (18)$$

$$\large \begin {align*} \color {purple} { \mathbf { K }’ } = \color {deeppink}{ \mathbf { P } _ k \mathbf { H } _ k ^ T } ( \color {deeppink} { \mathbf { H } _ k \mathbf { P } _ k \mathbf { H } _ k ^ T } + \color {mediumaquamarine} { \mathbf { R } _ k } ) ^ { - 1 } \end{align*} \;\;\;\;\;\;\;\; (19)$$

روابط اخیر معادلات کامل را برای مرحله به‌روزرسانی نشان می‌دهد. در نتیجه، $$\color{royalblue}{\mathbf{\hat{x}}_k’}$$ بهترین تخمین جدید است و می‌توانیم آن را به‌روز کنیم.

شکل زیر، الگوریتم فیلتر کالمن را نشان می‌دهد.

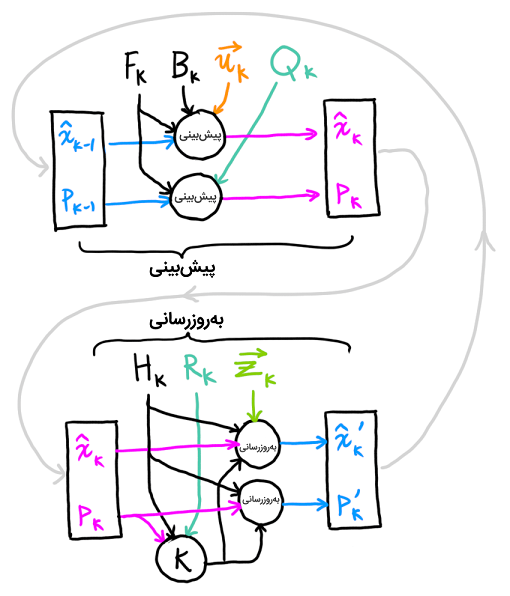
با توجه به مطالبی که در بالا گفته شد، تمام چیزی که برای پیاده‌سازی نیاز داریم، معادلات (۷)، (۱۸) و (۱۹) هستند. اگر این معادلات را فراموش کنیم، می‌توانیم دوباره همه چیز را از معادلات (۴) و (۱۵) استخراج کنیم. در این صورت می‌توانیم هر سیستم خطی را به صورت دقیق مدل کنیم. برای سیستم‌های غیرخطی، از فیلتر کالمن توسعه یافته استفاده می‌کنیم که به سادگی با خطی‌سازی پیش‌بینی‌ها و اندازه‌گیری‌ها حول میانگینشان کار می‌کند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• سیستم غیر خطی — راهنمای جامع
• کنترل بهینه در متلب — از صفر تا صد
• فیلتر کالمن بی اثر (UKF) — از صفر تا صد

^^