ظرفیت خازن — یادگیری با مثال

در مجموعه مقالات فرادرس با فیزیک خازن و رفتار آن در جریان‌های الکتریکی ثابت و متناوب و نحوه محاسبه ظرفیت معادل در مدارهای سری و موازی آشنا شدید. در این مقاله قصد داریم تا با زبانی ساده و ارائه چندین مثال به بحث محاسبه ظرفیت خازن با توجه به ساختار فیزیکی آن‌ها و استفاده از فرمول پایه‌ای $$C=\frac{Q}{V}$$ بپردازیم. با ما در ادامه این مطلب همراه باشید.

ظرفیت خازن

احتمالاً از دوران دبیرستان به یاد دارید که فرمول محاسبه ظرفیت خازن به صورت زیر است:

$$C=\epsilon\frac{A}{d}$$

که در رابطه فوق، $$A$$ مساحت صفحات خازن، $$d$$ فاصله بین صفحات و $$\epsilon$$ ضریب دی‌الکتریک برای محیط بین دو صفحه است. اگر دقت کرده باشید، برای معرفی پارامتر‌های موجود در فرمول فوق، از واژه «صفحه» استفاده کردیم. در واقع این فرمول، تنها برای خازن‌های تخت و ساده که از دو صفحه موازی تشکیل شده‌اند، کاربرد دارد.

فیلم آموزش فیزیک – پایه یازدهم در فرادرس

کلیک کنید

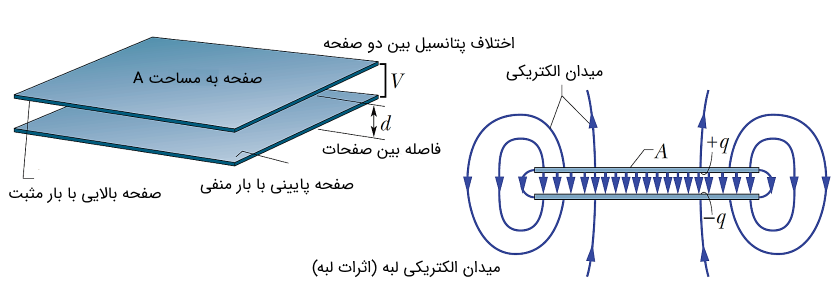
آیا تا به حال فکر کرده‌اید که چگونه می‌توان ظرفیت یک خازن با ساختار استوانه‌ای یا کروی را بررسی کرد؟ پاسخ در فرمول ساده $$C=\frac{Q}{V}$$ نهفته است. در واقع رابطه بین ظرفیت با مقدار بار ذخیره شده بر روی صفحات (نه لزوماً تخت) و ولتاژ دو سر خازن در بین انواع خازن‌ها برقرار بوده و به وسیله آن می‌توانیم ظرفیت خازن را محاسبه کنیم.

توجه داشته باشید که رابطه ساده $$C=\epsilon\frac{A}{d}$$، خود از رابطه $$C=\frac{Q}{V}$$ برای خازن‌هایی با صفحات تخت نتیجه می‌شود. برای استفاده از این فرمول، جهت محاسبه ظرفیت خازنی، تنها نیاز است تا مقدار بار $$Q$$ و ولتاژ $$V$$ را به دست آوریم. مطابق با این رابطه، واحد سنجش ظرفیت یک خازن، کولن (Coulomb) بر ولت (Volt) بوده که «فاراد» (Farad) نامیده می‌شود ($$1F=\frac{1C}{1V}$$). به دست آوردن $$Q$$ معمولاً به کمک قانون گاوس کار راحتی است. در مقاله «قانون گاوس (Gauss Law) و شار الکتریکی — یادگیری با مثال» با مفهوم و مثال‌های متعددی از قانون گاوس آشنا شدید. جهت یادآوری، این قانون به شکل زیر است:

$$\epsilon_{0}\oint E.dA=q$$
(1)

که در آن $$E$$ میدان الکتریکی داخل سطح گاوسی، $$q$$ بار محصور شده در سطح گاوسی، $$ds$$ دیفرانسیل (جز سطح) و $$\epsilon_{0}$$ گذرذهی الکتریکی خلأ است.

برای محاسبه ولتاژ $$V$$ نیز از رابطه انتگرالی آن با میدان الکتریکی $$E$$ استفاده می‌کنیم. رابطه مذکور به قرار زیر است:

$$V_{f}-V_{f}=\int_{i}^{f}E.dx$$
(2)

حال با محاسبه دو مقدار $$Q$$ و $$V$$ مطابق با گفته‌های فوق و جایگذاری آن‌ها در معادله $$C=\frac{Q}{V}$$، مقدار ظرفیت خازن مد نظر را به دست می‌آوریم. در ادامه این مقاله سعی داریم با ارائه چندین مثال، نحوه محاسبه ظرفیت خازنی را آموزش دهیم.

البته توجه داشته باشید که محاسبه ظرفیت خازن از طریقی که در این مقاله به آن اشاره شده است، تنها در آزمایشگاه و کلاس درس کاربرد دارد. در صنعت و پروژه‌های کاربردی معمولاً ظرفیت خازن را از طریق کدرنگی حساب می‌کنند. برای اطلاعات بیشتر به مقاله «کد رنگی خازن -- به زبان ساده» مراجعه کنید.

ظرفیت خازن تخت

در این قسمت می‌خواهیم به رابطه ساده $$C=\epsilon\frac{A}{d}$$ که از دوران دبیرستان آن را حفظ هستید، از طریق فرمول $$C=\frac{Q}{V}$$ برسیم. ساختار یک خازن با صفحات تخت که بین دو صفحه آن هوا است را مطابق شکل (۳) در نظر بگیرید. اولین قدم جهت استفاده از رابطه $$C=\frac{Q}{V}$$، به دست آوردن بار موجود در صفحات خازن است. یکی از راهکارهایی که اکثراً مفید واقع می‌شود، به دست آوردن مقدار بار از طریق قانون گاوس است.

$$\epsilon\oint E.dA=q$$
(1)

فیلم آموزش فیزیک 2 دانشگاه – جامع و با نکات کاربردی در فرادرس

کلیک کنید

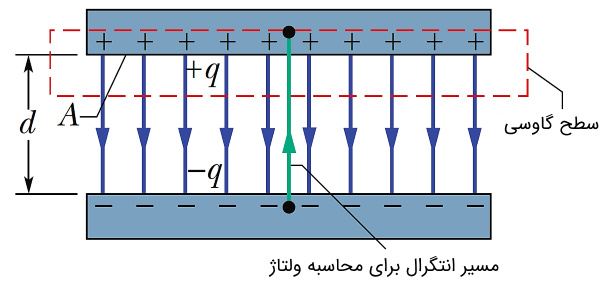
سطح فرضی گاوسی را مطابق شکل (3) در نظر بگیرید. از آنجا که مقدار میدان الکتریکی بین صفحات خازن ثابت بوده و با جزء دیفرانسیلی انتگرال تغییری نمی‌کند، می‌توانیم آن را به بیرون از انتگرال انتقال دهیم. توجه شود که از اثرات لبه (میدان در لبه‌ها) صرف نظر می‌کنیم. مساحت سطح گاوسی را نیز با $$A$$ نمایش می‌دهیم. در نتیجه از رابطه (۱) خواهیم داشت:

$$\epsilon E\oint dA=q$$
(2)

پس مقدار بار $$q$$ ذخیره شده بر روی صفحات خازن تخت با مساحت $$A$$ به صورت زیر در می‌آید:

$$\epsilon EA=q$$
(3)

از آنجا که بین دو صفحه خازن چیزی وجود ندارد، در رابطه فوق، $$\epsilon$$ را ضریب گذردهی الکتریکی خلأ با مقدار $$\epsilon_{0}\ =8.854\ 187\ 817\ \times 10^{-12}\frac{C^{2}}{Nm^{2}}$$ در نظر می‌گیریم.

قدم دوم به دست آوردن اختلاف پتانسیل بین دو صفحه خازن با استفاده از رابطه معروف زیر است.

$$V_{f}-V_{f}=\int_{i}^{f}E.dx$$
(4)

رابطه فوق بیان می‌کند که اختلاف پتانسیل بین دو نقطه $$i$$ و $$f$$ که در میدان الکتریکی $$E$$ قرار دارند، با انتگرال خطی میدان به صورت فوق، ارتباط دارد.

از آنجا که میدان الکتریکی بین دو صفحه خازن، ثابت و مستقل از جزء دیفرانسیلی است، به راحتی آن را از انتگرال بیرون می‌آوریم. در اینجا مسیر (بازه) انتگرال، فاصله بین دو صفحه خازن از یکدیگر یعنی $$d$$ است. پس ولتاژ خازن (اختلاف پتانسیل بین دو صفحه) به صورت زیر در می‌آید:

$$V=V_{f}-V_{f}=\int_{i}^{f}E.d=\int_{-}^{+}E.dx=E\int_{0}^{d}dx=Ed$$
(5)

حال که دو پارامتر $$q$$ و $$V$$ مربوط به خازن تخت را در اختیار داریم، به راحتی با استفاده از فرمول $$C=\frac{Q}{V}$$، ظرفیت خازن تخت را حساب می‌کنیم. با جای‌گذاری دو پارامتر مذکور داریم:

$$C=\frac{Q}{V}=\frac{\epsilon_{0} EA}{Ed}=\epsilon_{0}\frac{A}{d}$$
(6)

مثال

یک خازن با صفحات تخت بزرگ که مساحت هر صفحه آن 0.5 متر مربع است، را در نظر بگیرید. فاصله بین صفحات 4 میلی‌متر و بین آن‌‌ها هوا است. اگر این خازن را به ولتاژ 6000 ولت متصل کنیم، چه مقدار بار روی صفحات آن ذخیره می‌شود؟

ابتدا ظرفیت خازن را به شکل زیر حساب می‌کنیم. برای سادگی روند محاسبات مقدار $$\epsilon_{0}$$ را $$\frac{1}{36\pi \times10^{9}}$$ در نظر میگیریم.

$$C=\epsilon_{0}\frac{A}{d}=\frac{1}{36\pi \times10^{9}}\frac{0.5}{4 \times10^{-3}}=1.1nF$$

حال با استفاده از رابطه $$Q=CV$$ می‌توانیم مقدار بار ذخیره شده بر روی صفحات خازن مذکور را به دست آوریم:

$$Q=CV=1.1nF\times6000V=6.6\mu C$$

ظرفیت خازن استوانه‌ ای

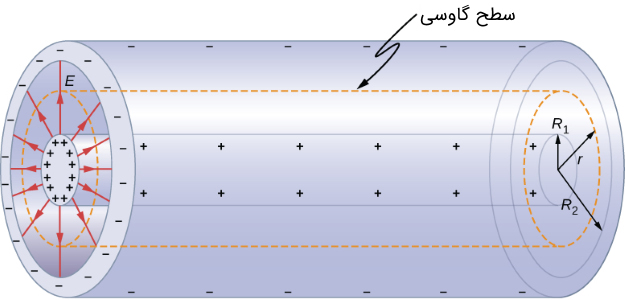
در مورد محاسبه ظرفیت خازن استوانه‌ای نیز همان راهکاری را پیش می‌گیریم که در محاسبه ظرفیت خازن تخت در بخش قبل از آن استفاده کردیم. قدم اول به دست آوردن میدان الکتریکی به وسیله قانون گاوس است. مطابق با شکل (4) یک استوانه فرضی به طول خازن را به عنوان سطح گاوسی در نظر می‌گیریم.

فیلم آموزش فیزیک 2 دانشگاه – جامع و با نکات کاربردی در فرادرس

کلیک کنید

مساحت این سطح گاوسی برابر با $$2\pi rL$$ (مساحت استوانه) بوده که در آن $$r$$ فاصله از مرکز خازن (شعاع استوانه فرضی) است. در اینجا نیز میدان الکتریکی یکنواخت بوده و با جز دیفرانسیلی تغییر نمی‌کند. قانون گاوس را به شکل زیر می‌نویسیم:

$$\epsilon\oint E.dA=q \Rightarrow \epsilon E\oint dA=\epsilon E2\pi rL=q$$
(1)

از قانون گاوس نتیجه می‌شود:

$$E=\frac{q}{\epsilon2\pi rL}$$
(2)

قدم دوم به دست آوردن ولتاژ خازن (اختلاف پتانسیل بین صفحات) است. باز هم از رابطه آشنای زیر برای محاسبه ولتاژ استفاده می‌کنیم. در اینجا $$E$$ را از قانون گاوس که در بالا به دست آوردیم، نوشته و انتگرال را حل می‌کنیم. دقت کنید که در اینجا بازه (مسیر) انتگرال روی مسیری است که دو صفحه استوانه داخلی و خارجی را به هم وصل می‌کند (شعاعی).

$$V=V_{f}-V_{f}=\int_{i}^{f}E.dr=\int_{R_{1}}^{R_{2}}\frac{q}{\epsilon2\pi rL}.dr=\frac{q}{\epsilon2\pi L}\int_{R_{1}}^{R_{2}}\frac{dr}{r}=\frac{q}{\epsilon2\pi L}Ln(\frac{R_{2}}{R_{1}})$$
(3)

با فرض اینکه محیط بین استوانه‌ داخلی و خارجی (صفحات استوانه‌ای خازن) را هوا در نظر گرفتیم، $$\epsilon$$ را ضریب گذردهی الکتریکی خلأ $$\epsilon_{0}$$ فرض می‌کنیم. حال با جای‌گذاری دو پارامتر $$q$$ و $$V$$ به دست آمده در رابطه $$C=\frac{Q}{V}$$، ظرفیت خازن استوانه‌ای به طول $$L$$ با شعاع داخلی $$R_{1}$$ و شعاع خارجی $$R_{2}$$ به صورت زیر به دست می‌آید:

$$C=\frac{Q}{V}=2\pi\epsilon_{0}\frac{L}{Ln(\frac{R_{2}}{R_{1}})}$$
(4)

مثال

یک کابل هم‌محور از یک استوانه داخلی به شعاع $$R_{1}$$ و یک پوسته استوانه‌ای شکل خارجی به شعاع $$R_{۲}$$ ساخته شده است. فضای بین دو پوسته، از هوا پر شده است. ولتاژ الکتریکی را در فاصله‌ی بین دو پوسته بر حسب فاصله شعاعی به دست آورید.

می‌دانیم که میدان الکتریکی در فاصله $$r$$ از یک توزیع بار خطی به صورت زیر است:

$$E=\frac{\lambda}{2\pi\epsilon_{0}r}$$

برای به دست آوردن پتانسیل در فاصله $$r$$، پتانسیل پوسته داخلی را $$V_{0}$$ فرض کرده و از رابطه زیر اقدام می کنیم:

$$V_{r}-V_{0}=-\int_{R_{1}}^{r}\frac{\lambda}{2\pi\epsilon_{0}r}dr=-\frac{\lambda}{2\pi\epsilon_{0}}Ln(\frac{r}{R_{1}})$$

ظرفیت خازن کروی

به احتمال زیاد تا به اینجای مقاله، با اصول و روند محاسبه ظرفیت یک خازن آشنا شده‌اید. در اینجا هم مطابق روند دو بخش قبلی، مقدار بار یا میدان را از طریق قانون گاوس به دست‌ می‌آوریم. متناسب با ساختار خازن یک سطح کروی به شعاع r را بین دو صفحه خازن در نظر می‌گیریم. مطابق با قانون گاوس داریم:

$$\epsilon_{0}\oint E.dA=q \Rightarrow \epsilon E\oint dA=\epsilon E4\pi r^{2}=q$$
(1)
$$E=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r^{2}}$$
(2)

فیلم آموزش مدارهای الکتریکی 1 – مرور و حل تست در فرادرس

کلیک کنید

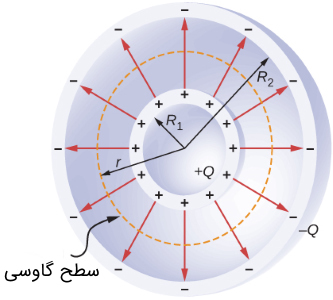
حال می‌خواهیم ولتاژ خازن را محاسبه کنیم. میدان الکتریکی E را که در بالا به دست آوردیم در رابطه زیر گذاشته و انتگرال را محاسبه می‌کنیم. در اینجا حدود انتگرال حد فاصل دو کره داخلی و خارجی است (شعاعی). یادآور می‌شویم که هدف ما به دست آوردن مقدار ولتاژ بین دو صفحه کره‌ای شکل خازن است.

$$V=V_{f}-V_{f}=\int_{i}^{f}E.dr=\int_{R_{1}}^{R_{2}}\frac{1}{4\pi\epsilon_{0}}\frac{q}{r^{2}}.dr=\frac{q}{4\pi\epsilon_{0}}\int_{R_{1}}^{R_{2}}\frac{dr}{r^{2}}=\frac{q}{4\pi\epsilon_{0}}(\frac{1}{R_{2}}-\frac{1}{R_{1}})$$
(3)

حال به راحتی از فرمول $$C=\frac{Q}{V}$$ ظرفیت خازن را به صورت زیر محاسبه می‌کنیم:

$$C=\frac {4\pi\epsilon_{0}} {\left (\frac {1}{R_2}-\frac {1}{R_1}\right)} ={4\pi\epsilon_{0}}\frac{R_{2}R_{1}}{R_{1}-R_{2}}$$

(4)

ظرفیت کره ایزوله

فرض کنید یک کره رسانا به شعاع R در اختیار دارید؟ به نظر شما ظرفیت این کره چقدر است؟ منظورمان این است که چه مقدار بار می‌تواند بر روی آن قرار گیرد؟ اگر این کره را کره داخلی یک خازن کروی بسیار بزرگ (یعنی شعاع کره خارجی در بی‌نهایت است) در نظر بگیریم، از رابطه ظرفیت خازن کروی که آن را در بالا به دست آوردیم، ظرفیت این کره را به صورت زیر به دست می‌آوریم:

$$C=\frac {4\pi\epsilon_{0}} {\left (\frac {1}{R_2}-\frac {1}{R_1}\right)} \Rightarrow R_{2}\rightarrow\infty \Rightarrow C=4\pi \epsilon _ 0 R_1 = 4\pi \epsilon _ 0 R$$

(5)

مثال

فرض کنید زمین یک رسانای منزوی (کُره تنها) باشد. ظرفیت چنین کره‌ای چقدر است؟ (شعاع زمین 6400 کیلومتر در نظر بگیرید)

دیدیم که ظرفیت یک رسانای کروی منزوی از رابطه زیر به دست می‌آید:

$$C=4\pi\epsilon_{0}R$$

با جایگذاری شعاع زمین در رابطه داریم:

$$C=4\pi\epsilon_{0}R=4\pi\frac{1}{36\pi \times10^{9}}6400\times10^{3}\approx700\mu F$$

مثال

دو کره رسانا به شعاع‌های $$x$$ و $$y$$ که در فاصله دوری از یکدیگر قرار دارند را به وسیله سیم نازک رسانایی به یکدیگر وصل می‌کنیم. به یکی از کره‌ها بار $$Q$$ را می‌دهیم. ظرفیت مجموعه مذکور (دو کره متصل) را به دست آورید.

از آنجایی که دو کره را به یکدیگر متصل کرده‌ایم، دو کره هم‌پتانسیل می‌شوند. در نتیجه پتانسیل مجموعه که آن را به $$V$$ نشان می‌دهیم برابر با پتانسیل هر یک از کره‌ها، به شکل زیر است:

$$V=\frac{q_{1}}{4\pi \epsilon_{0}x}=\frac{q_{2}}{4\pi \epsilon_{0}y}$$

از رابطه فوق نتیجه می‌شود:

$$\frac{q_{1}}{x}=\frac{q_{2}}{y}$$

از آنجایی که مقدار بار کل $$Q$$ برابر با مجموعه بارهای دو کره است ($$Q=q_{1}+q_{2}$$)، داریم:

$$q_{1}=(\frac{x}{x+y})Q \ , \ q_{2}=(\frac{y}{x+y})Q$$

با جایگذاری بار $$q_{1}$$ یا $$q_{2}$$ در رابطه $$V$$ و استفاده از رابطه $$C=\frac{Q}{V}$$ داریم:

$$V=\frac{Q}{4\pi \epsilon_{0}(x+y)}\Rightarrow C=\frac{Q}{V}=4\pi \epsilon_{0}(x+y)$$

ظرفیت خازن تخت با دی‌ الکتریک

در دروس فیزیک پایه، دیدیم که با قرار دادن یک دی‌الکتریک بین صفحات یک خازن می‌توانیم ظرفیت‌ خازن را افزایش دهیم. در واقع با قرار دادن دی‌الکتریک، بارهای بیشتری بر روی صفحات خازن می‌توانند قرار گیرند. در این قسمت می‌خواهیم با استفاده از قانون گاوس، ظرفیت یک خازن با صفحات تخت حاوی ماده دی‌الکتریک را به دست آوریم.

فیلم آموزش مدارهای الکتریکی ۱ – جامع و کاربردی در فرادرس

کلیک کنید

به طور خیلی خلاصه، با قرار دادن یک ماده دی‌الکتریک در بین صفحات خازن، به دلیل وجود میدان الکتریکی بین دو صفحات، دو قطبی‌هایی در داخل ماده دی‌الکتریک القا می‌شوند. می‌دانیم که بارهای مثبت در جهت میدان و بارهای منفی در خلاف جهت میدان الکتریکی می‌روند (شکل 6). این القای دو قطبی و جدایی بار باعث به وجود آمدن میدان الکتریکی داخلی در داخل ماده دی‌الکتریک می‌شود که با توجه به شکل (6) در خلاف جهت میدان اصلی (میدان بدون حضور ماده دی‌الکتریک) بوده و آن را تضعیف می‌کند.

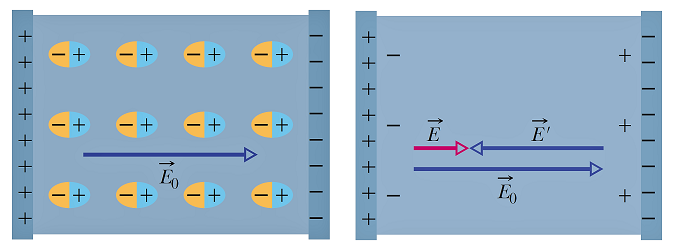
می‌دانیم که میدان الکتریکی و ولتاژ طبق رابطه ($$V_{f}-V_{f}=\int_{i}^{f}E.dx$$) در ارتباط هستند. مطابق رابطه مذکور با کاهش مقدار میدان الکتریکی، مقدار ولتاژ نیز باید کاهش پیدا کند. اما از آنجا که خازن به یک ولتاژ با ظرفیت ثابت متصل است، نتیجه می‌گیریم که برای جبران میدان افت پیدا کرده، مقدار بار بیشتری بر روی صفحات خازن جمع می‌شود.

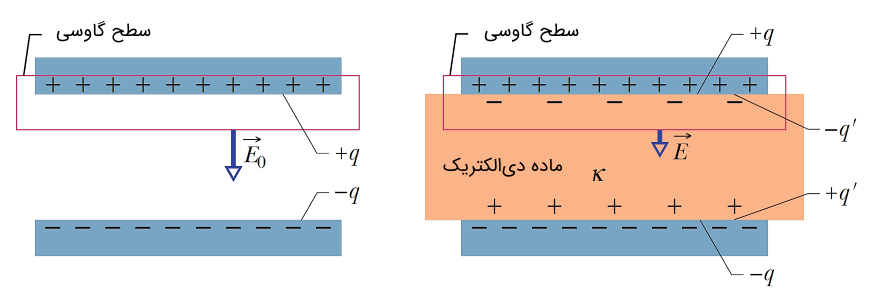
با توضحیات فوق، حال بیایید قانون گاوس را برای خازن با صفحات تخت حاوی ماده دی‌الکتریک بنویسیم. طبق شکل (7)، سطح گاوسی این‌ بار علاوه بر بار صفحه، بار حاصل از دوقطبی‌های القا شده را نیز در بر می‌گیرد. پس قانون گاوس به شکل زیر در می‌آید:

$$\epsilon\oint E.dA=q-q^{'}$$
(1)

در اینجا نیز میدان الکتریکی E وابستگی به جزء دیفرانسیلی نداشته و از انتگرال بیرون می‌آید. با مرتب سازی بر حسب میدان $$E$$ داریم:

$$E=\frac{q-q^{'}}{\epsilon_{0} A}$$
(2)

مشاهده می‌شود که این میدان طبق توضیحات فوق، مقدار کمتری نسبت به میدان الکتریکی $$E_{0}$$ (بدون ماده دی‌آلکتریک) دارد. می‌توانیم این میدان را به صورت ضریبی از میدان $$E_{0}$$ بنویسیم. در نتیجه داریم:

$$E=\frac{E_{0}}{k}=\frac{q}{k\epsilon_{0} A}$$
(3)

با مقایسه دو رابطه (۱) و (۳) پی می‌بریم:

$$q-q^{'}=\frac{q}{k}$$
(4)

در نتیجه قانون گاوس به شکل زیر در می‌آید:

$$\epsilon_{0}\oint kE.dA=q$$
(5)

در اینجا می‌توان کمیت جدیدی را به نام چگالی شار الکتریکی به صورت زیر تعریف کرد:

$$D=\epsilon E=k\epsilon_{0}E$$
(6)

از رابطه (۵) به همان ترتیب که برای خازن تخت بدون ماده دی‌الکتریک عمل کردیم، ظرفیت خازن تخت با ماده دی‌الکتریک به صورت زیر در می‌آید:

$$C=k\epsilon_{0}\frac{A}{d}$$
(7)

مقدار $$k$$ برای هوا یا خلأ برابر با یک در نظر گفته می‌شود. رابطه فوق در واقع همان رابطه $$C=\epsilon\frac{A}{d}$$ بوده که در حالت کلی مقدار $$\epsilon$$ را به صورت زیر تعریف می‌کنند:

$$\epsilon=k\epsilon_{0}\Rightarrow k \equiv\epsilon_{r}=\frac{\epsilon}{\epsilon_{0}}>1$$
(8)

$$\epsilon_{r}$$ به گذردهی نسبی معروف است.

مثال

خازن تختی را در نظر بگیرید که فاصله بین صفحات آن ۴ میلیمتر بوده و به یک باتری 160 ولتی متصل شده است. ماده دی‌الکتریکی با $$k=4$$ را بین صفحات آن، به طوری که بین صفحات را کامل پر کند، قرار می‌دهیم. میدان الکتریکی و چگالی شار الکتریکی را در دو حالت قبل و بعد از وجود ماده دی‌الکتریک به دست‌ آورید:

برای محاسبه میدان الکتریکی و چگالی شار الکتریکی قبل از قرار دادن ماده دی‌الکتریک به صورت زیر عمل می‌کنیم:

  $$V_{f}-V_{f}=\int_{i}^{f}E.dx \Rightarrow V=Ex \Rightarrow E=\frac{V}{x}=\frac{160}{4\times10^{-3}}=40(\frac{kV}{m})$$

$$D=\epsilon_{0}E=\frac{1}{36\pi \times10^{9}}40=35.38\times10^{-8}(\frac{C}{m^{2}})$$

پس از قرار دادن ماده دی‌الکتریک با $$k=4$$، به علت القای دو قطبی و تشکیل میدانی در خلاف جهت میدان اصلی (شکل ۷)، میدان الکتریکی کاهش پیدا میکند. در نتیجه:

$$E=\frac{E_{0}}{k}=10(\frac{kV}{m})$$

$$D=\epsilon E=k\epsilon_{0}E=35.38\times10^{-8}(\frac{C}{m^{2}})$$

ملاحظه شود که مقدار چگالی شار الکتریکی بدون تغییر می‌ماند. چرا که با افزایش ثابت دی‌الکتریک $$k$$، میدان به همان نسبت کاهش پیدا می‌کند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش فیزیک پایه ۲
• مجموعه آموزش‌های دروس مهندسی برق
• آموزش مدارهای الکتریکی ۱
• مدار RLC — از صفر تا صد
• فیبر نوری — به زبان ساده