شدت موج — به زبان ساده

پیش‌تر در وبلاگ فرادرس در مورد امواج الکترومغناطیسی، نحوه تولید آن‌ها و هم‌چنین تداخل آن‌ها صحبت کردیم. از این رو در این مطلب قصد داریم تا در مورد مفهومی تحت عنوان شدت موج بحث کرده و مثال‌هایی را نیز از آن ارائه دهیم.

شدت موج

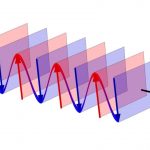
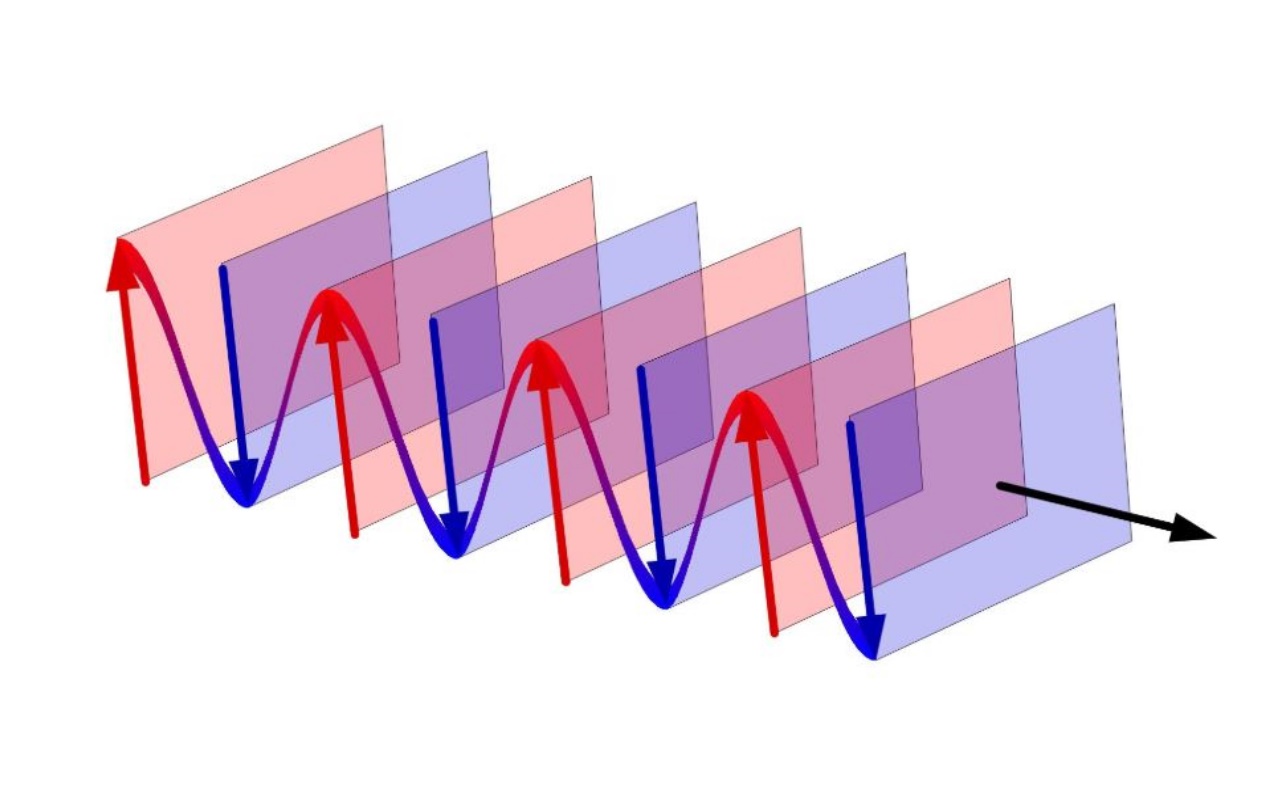
تمامی امواج چه از نوع امواج مکانیکی و چه از نوع الکتریکی، منتقل‌کننده انرژی هستند. با تقریب خوبی می‌توان گفت میزان انرژی منتقل شده توسط موج، وابسته به توان دوم دامنه $$S _ { m a x }$$ و توان دوم فرکانس $$f$$ آن است. به طور دقیق‌تر می‌توان گفت:

$$P _ { a v g } \propto S _ { \max } ^ { 2 } f ^ { 2 }$$

در رابطه فوق $$P$$ نشان‌دهنده توان منتقل‌شده توسط موج است. در این صورت شدت موج یا $$I$$ برابر با مقداری از انرژی است که در سطح عمود بر جهت انتشار موج قرار دارد. در نتیجه این مقدار برابر است با:

$$\begin {aligned} I & = \frac { P _ { a w g } } { A } \\ I & = C \left( \frac { S _ { \max } ^ { 2 } f ^ { 2 } }{ A } \right) \end {aligned}$$

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

کلیک کنید

$$C$$ ثابتی است که نحوه تغییرات شدت، نسبت به فرکانس و دامنه را نشان می‌دهد. اگر یک موج از منبعی مشخص در تمامی جهات منتشر شود، در این صورت موج مذکور کروی نامیده می‌شود. در حالی که موج منتشر می‌شود، مساحت منتقل‌کننده انرژی نیز افزایش می‌یابد.

اگر شعاع کره برابر با $$R$$ و توان خروجی نیز ثابت و برابر با $$P$$ باشد، در این صورت مقدار شدت را می‌توان با استفاده از رابطه زیر توضیح داد.

$$I = \frac { P } { 4 \pi R ^ { 2 } } \quad I \propto \frac { 1 } { R ^ { 2 } }$$

به رابطه فوق معمولا قانون مربع معکوس گفته می‌شود.

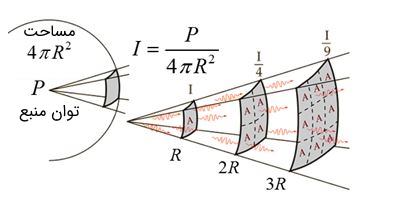
توجه داشته باشید که مقدار توان در فواصل مختلف یکسان است. برای نمونه دو نقطه از موج زیر را در فاصله $$R _ 1$$ و $$R _ 2$$ در نظر بگیرید.

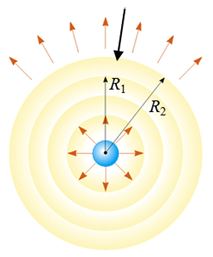
برای نقاط فوق می‌توان دو رابطه زیر را برای شدت موج در دو فاصله مختلف بیان کرد:

$$I _ { 1 } = \frac { P } { 4 \pi R _ { 1 } ^ { 2 } } \quad I _ { 2 } = \frac { P } { 4 \pi R _ { 2 } ^ { 2 } } \Rightarrow \frac { I _ { 2 } } { I _ { 1 } } = \frac { R _ { 1 } ^ { 2 } } { R _ { 2 } ^ { 2 } }$$

برای نمونه اگر فاصله تا منبع دو برابر شود، در این صورت شدت نیز $$\frac { 1 } { 4 }$$ می‌شود. دلیل این امر نیز رابطه زیر است.

$$\left( \frac { R _ { 1 } } { R _ { 2 } } \right) = \frac { 1 } { 2 } \quad \frac { I _ { 2 } }{ I _{ 1 } }‌ = \left( \frac { R _ { 1 } } { R _ { 2 } } \right) ^ { 2 } = \left( \frac { 1 } { 2 } \right) ^ { 2 } = \frac { 1 } { 4 }$$

توجه داشته باشید که دامنه موج نیز با فاصله گرفتن از منبع، کم می‌شود. با توجه به اینکه شدت موج وابسته به توان دوم آن است، بنابراین می‌توان گفت خودِ‌ دامنه نیز متناسب با معکوس فاصله از منبع است. در نتیجه می‌توان رابطه زیر را بیان کرد:

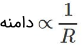
برای نمونه دامنه موج زمانی که فاصله موج از منبع دو برابر شود، نصف می‌شود. جبهه موج، خط یا صفحه‌ای است که در آن نقاط هم‌فاز قرار گرفته‌اند. شکل زیر جبهه یک موج ایجاد شده در آب را نشان می‌دهد.

در مورد آب، همان‌طور که در بالا نیز نشان داده شده، جبهه‌های موج به صورت دایره‌ای و در مورد مثلا امواج صوتی، امواج به صورت کروی هستند. در مدل‌سازی یک‌بعدی، معمولا امواج را به صورت تخت در نظر می‌گیرند.

مثال

یک نقطه که به عنوان منبعی صوتی است، امواج صوتی را با فرکانس $$50W$$ در فضای اطراف منتشر می‌کند. در این صورت شدت موج صوتی منتشر شده را در فواصل 1، ۲ و ۱۰ متری بدست آورید. همچنین میزان انرژی دریافت شده در فاصله ۱ متری، توسط آشکارسازی به مساحت $$123 \ m m ^ 2$$ را بدست آورید. فرض کنید این سطح به مدت ۱۰ ثانیه در معرض این موج قرار گرفته است.

فرضیات مسئله در ادامه ارائه شده‌اند.

$$\begin{array} { l l } { \ P=50 \mathrm { W } } \\ { R _ { 1 } = 1.00 \mathrm { m } \quad I _ { 1 } = ? \mathrm { W . m } ^ { - 2 } \quad A _ { D } = 123 \mathrm { m m } ^ { 2 } = 123 \times 10 ^ { - 6 } \mathrm { m } ^ { 2 } \quad \Delta t = 10 \mathrm { s } } \\ { R _ { 2 } = 5.00 \mathrm { m } \quad I _ { 2 } = ? \mathrm { W . m } ^ { - 2 } } \\ { R _ { 3 } = 10.0 \mathrm { m } \quad I _{ 3 } = ? \mathrm { W . m } ^ { - 2 } } \end{array}$$

شدت نیز متناسب با معکوس توان دوم فاصله تغییر می‌کند. در نتیجه با استفاده از رابطه $$I = \frac { P } { 4 \pi R ^ { 2 } }$$، مقادیر شدت برابر می‌شوند با:

$$I _ { 1 } = 4 . 0 \mathrm { W . m } ^ { - 2 } \quad I _ { 2 } = 1 . 0 \mathrm { W . m } ^ { - 2 } \quad I _ { 3 } = 0.04 \mathrm { W . m }^ { - 2 }$$

به منظور بدست آوردن انرژی دریافتی در فاصله ۱ متری باید در ابتدا توان عبوری را در این فاصله بدست آوریم. مقدار این توان برابر است با:

$$P _ { D } = I _ { D } A _ { D }$$

$$4 .0 \ \mathrm{ W } \cdot \mathrm { m } ^ { - 2 } × 123 \times 10 ^ { - 6 } \mathrm { m } ^ 2 = 4. 9 × 10 ^ { - 4 } W$$

در نتیجه مقدار انرژی دریافتی در مدت زمان ۱۰ ثانیه برابر است با:

$$\Delta E _ { D } = 4 . 9 \times 10 ^ { - 3 } \mathrm { J }$$

در صورتی که مطلب فوق برای شما مفید بوده است آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس فیزیک
• مجموعه آموزش‌‌های ریاضی
• امواج الکترومغناطیسی — از صفر تا صد
• فرکانس — به زبان ساده
• فوتون در فیزیک — به زبان ساده
• اثر فوتوالکتریک (Photoelectric Effect) — به زبان ساده