سیستم غیر خطی – راهنمای جامع

سیستم غیر خطی گستره وسیعی از سیستم‌های موجود در طبیعت را در بر می‌گیرد. در اکثر موارد، سیستم را می‌توان توسط یک مدل خطی ساده‌تر تقریب زد. در این موارد اثر غیر خطی بودن (Nonlinearity) کوچک است و می‌توان از آن صرف نظر کرد. اما این ایده همیشه درست نیست. بسته به نوع غیر خطی بودن، حالت‌های سیستم می‌توانند رفتار همگرا (Convergent)، واگرا (Divergent) یا نوسانی (Cyclic) داشته باشند. در این مطلب قصد داریم تا سیستم‌های غیر خطی را معرفی کنیم و به بیان روش‌های آنالیز پایداری بپردازیم. همچنین این مفاهیم را با ذکر چند مثال ساده، واضح‌تر خواهیم ساخت.

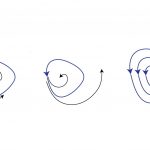
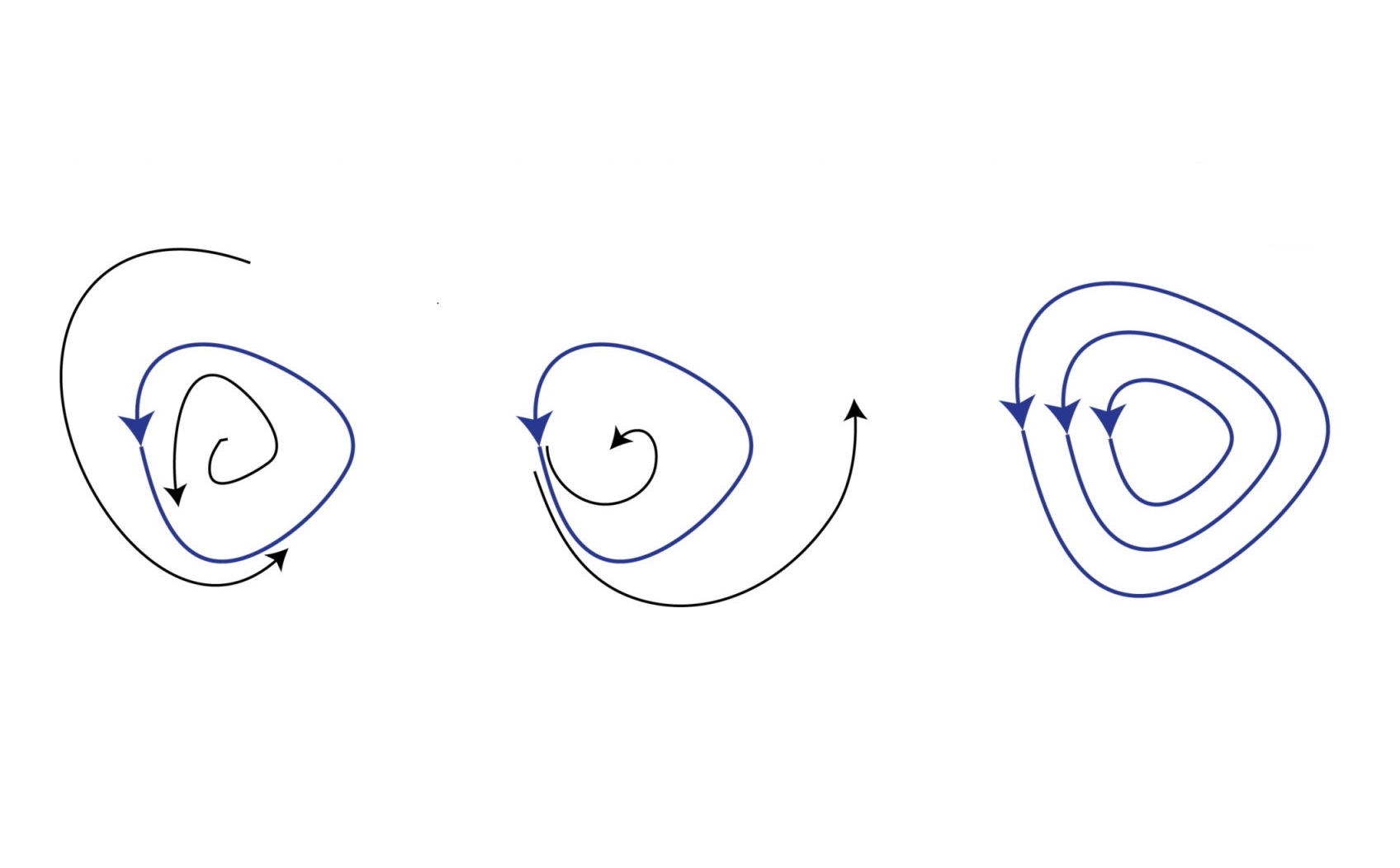
یک مثال ساده از یک خودروی زیرآبی (Underwater Vehicle) را در نظر بگیرید که معادله آن به صورت زیر است:

$$\ddot{x} = u - \dot{x} |\dot{x}|$$

عبارت $$\dot{x} |\dot{x}|$$ نشان‌دهنده اصطکاک ناشی از آب است.

در این مورد، حالت خاصی را که در آن ورودی کنترل $$u = 0$$ است بررسی می‌کنیم. پس معادله سیستم برابر است با:

$$\ddot{x} = - \dot{x} | \dot{x} |$$

این سیستم زمانی که $$\dot{X}>0$$، دارای مشتق منفی و زمانی که $$\dot{X}<0$$، دارای مشتق مثبت است. بنابراین نرخ رشد حالت‌های سیستم همواره کاهشی است. در نتیجه می‌توان گفت که سیستم همواره پایدار است. این نوع غیر خطی بودن را اتلافی (Dissipative) یا پایدار‌کننده (Stabilizing) می‌نامند.

اما همیشه به این صورت نیست و ممکن است غیر خطی بودن منجر به ناپایداری حالت‌های سیستم شود. سیستم زیر را در نظر بگیرید:

$$\ddot{x} = u - x^2$$

در این سیستم اگر حالت‌های سیستم با یک مقدار مثبت شروع شوند، گرادیان آن‌ها منفی می‌شود و حالت‌های سیستم به صفر کاهش می‌یابند. اما اگر مقدار اولیه $$x$$ منفی باشد، گرادیان عددی منفی می‌شود و حالت سیستم به $$-\infty$$ می‌رود. در این حالت نوع غیر خطی بودن، غیراتلافی (Non-dissipative) یا ناپایدارکننده (Destabilizing) نامیده می‌شود.

بنابراین بسته به نوع غیر خطی بودن، یک سیستم می‌تواند پایدار یا ناپایدار شود. یک سیستم غیر خطی مشخصه جالب دیگری را نیز از خود نشان می‌‌دهد. حالت‌های یک سیستم غیر خطی می‌توانند حرکتی نوسانی را تجربه کنند که در آن هیچ‌گاه به یک مقدار ثابت همگرا و یا به بی‌نهایت واگرا نشوند.

نوسان‌ساز وندر پل

یک سیستم غیر خطی مرتبه دوم که بسیار مورد بررسی قرار می‌گیرد، نوسان‌ساز وندر پل (Van der Pol Oscillator) است. فرم این سیستم به صورت زیر است:

$$\ddot{X} + u(X) \dot{X} + V(X) = 0$$

که در آن $$u(X)$$ و $$V(X)$$ می‌توانند به عنوان چسبندگی (Viscosity) و سختی (Stiffness) در نظر گرفته شوند. حالت خاصی را در نظر بگیرید که:

$$\ddot{X} - \mu (1- X^2) \dot{X} + X = 0$$

معادله بالا در فرم فضای حالت به صورت زیر نشان داده می‌شود:

$$\dot{X_2} = \mu (1- X_1^2) X_2 - X_1$$

در معادله بالا $$\mu$$ پارامتر میرایی (Damping) است. یک راه متداول برای به تصویر کشیدن رفتار یک سیستم غیر خطی، رسم یک حالت بر حسب حالت‌های دیگر است و معمولا یک متغیر بر حسب مشتق آن رسم می‌شود. به دیاگرام ترسیم‌شده پرتره فاز می‌گویند. قطعه کد زیر، نحوه رسم حالت‌های سیستم بالا در MATLAB را نشان می‌دهد.

شکل زیر حالت‌های سیستم را نشان می‌دهد.

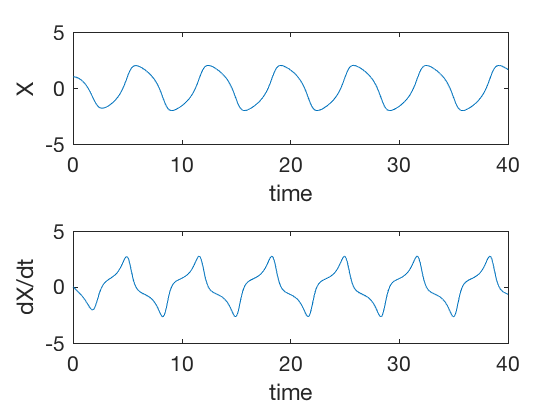
حال کد زیر پرتره فاز سیستم را رسم می‌کند.

پرتره فاز سیستم به صورت زیر است.

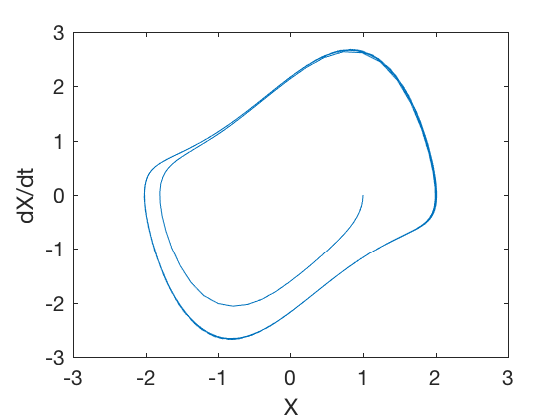
همان‌طور که از شکل بالا مشخص است، علی‌رغم شرایط اولیه سیستم، حالت‌ها به یک چرخه نوسانی همگرا می‌شوند. به این چرخه نوسانی، چرخه حدی (Limit Cycle) می‌گویند. بنابراین علاوه بر این‌که حالت‌ها می‌توانند به یک مقدار ثابت همگرا شوند و یا به بی‌نهایت واگرا شوند، این امکان نیز وجود دارد که حالت‌ها رفتاری دوره‌ای از خود نشان دهند که به آن چرخه حدی می‌گویند. طبقه خاصی از سیستم‌های غیر خطی که چنین رفتار نوسانی را از خود نشان می‌دهند، سیستم‌های لینارد (Lienard) نامیده می‌شوند.

سیستم‌های لینارد

معادله دیفرانسیل زیر را در نظر بگیرید:

$$y_1 = f_1(t,X)$$

$$y_2 = f_2(t,X)$$

اگر به ازای چند $$f_1$$ و $$f_2$$ داشته باشیم:

$$\frac{\partial f_1}{\partial t} + \frac{\partial f_2}{\partial t} \neq 0$$

آن‌گاه چرخه حدی وجود نخواهد داشت. اگر عبارت سمت چپ برابر با صفر باشد، وجود یک چرخه حدی امکان نخواهد داشت. برای نوع خاصی از سیستم‌های Lienard که می‌توانند به صورت زیر بیان شوند، از تئوری Lienard برای بررسی وجود چرخه حدی استفاده می‌شود.

$$\ddot{X} + F'(X) \dot{X} + G'(X) = 0,$$

تئوری لینارد برای چرخه حدی

تئوری لینارد بیان می‌کند که اگر دو تابع نرم و فرد $$F$$ و $$G'$$ داشته باشیم، به نحوی که برای $$X>0$$، $$G'(X)>0$$ و همچنین تابع $$F$$ دقیقا دارای سه صفر در $$0$$ و $$a$$ و $$-a$$ باشد و $$F’(0) < 0$$ و $$F’(X) ≥ 0$$ برای $$X > a$$ برقرار باشند و نیز $$F(X) → ∞$$ اگر $$X →∞$$، آنگاه سیستم Lienard متناظر با آن دقیقا دارای یک چرخه حدی است و این چرخه پایدار است.

توجه کنید که عبارت بالا بیان می‌کند که مشتق تابع $$F$$ اگر $$X$$ بزرگتر از صفر باشد، افزایش می‌یابد و اگر $$X$$ بزرگتر از $$a$$ باشد، کاهش می‌یابد. این شروط منجر به سیستمی می‌شوند که در آن حالت‌های سیستم از صفر دور شده و به جای همگرایی به یک مقدار ثابت، به یک مسیر دورانی (Orbit) نوسانی همگرا می‌شوند. اگر $$F$$ و $$G$$ به صورت زیر انتخاب شوند:

$$F(X) = \mu \left( \frac{X^3}{3}-X \right)$$

$$G(X) = \frac{X^2}{2},$$

$$\ddot{X} + F'(X) \dot{X} + G'(X) = 0$$

آن‌گاه سیستم به صورت زیر نوشته خواهد شد:

$$\ddot{X} - \mu \left( 1 - X^2 \right) \dot{X} + G'(X) = 0$$

معادله بالا معادله یک نوسان‌ساز وندر پل است. بنابراین بر اساس نوع غیر خطی بودن و مقدار اولیه، حالت‌های یک سیستم ممکن است به یک نقطه ثابت همگرا شوند یا یک حرکت نوسانی داشته باشند و یا واگرا شوند. تکنیک‌های خاصی برای مطالعه مشخصه‌های سیستم غیر خطی گسترش یافته‌اند که در ادامه به بیان آن‌ها می‌پردازیم.

تکنیک‌های آنالیز پایداری سیستم‌ غیر خطی

سیستم غیر خطی در دو مد، رفتار پایداری از خود نشان می‌دهند. این سیستم‌ها ممکن است یا یک نقطه تعادل (Equilibirum) داشته باشند که حالت‌های سیستم به آن همگرا شوند و یا یک چرخه حدی داشته باشند که حالت‌ها رفتاری نوسانی را تجربه کنند.

فیلم آموزش طراحی فیدبک حالت بهینه برای سیستم های غیر خطی با الگوریتم های تکاملی در فرادرس

کلیک کنید

نقطه تعادل

سیستمی را که توسط معادله زیر توصیف می‌شود در نظر بگیرید:

$$\dot{X} = f(X)$$

یک نقطه $$X_{eq}$$ نقطه تعادل نامیده می‌شود اگر شرط زیر برقرار باشد:

$$f( X_{eq}) = 0$$

این نقطه تعادل باید پایدار باشد. اگر در همسایگی $$X_{eq}$$، جهت مشتق از آن دور شود، حالت‌ها حرکت خواهند کرد.

چرخه حدی

همان‌طور که در بالا بررسی کردیم، چرخه حدی مسیر دورانی نوسانی است که حالت‌های یک سیستم غیر خطی در آن مسیر مستقر می‌شوند. برای کاربردهایی که در آن‌ها هدف ایجاد حرکت نوسانی است، چرخه حدی یک مشخصه بسیار مفید است. یافتن یک چرخه معمولا بسیار دشوار است. چرخه‌های حدی می‌توانند پایدار، ناپایدار و یا نیمه‌پایدار (Half Stable) باشند. چرخه‌های حدی نیمه‌پایدار چرخه‌هایی هستند که برای مقادیر اولیه که داخل ناحیه محاصره شده توسط چرخه حدی باشند، پایدار بوده و برای سایر نواحی ناپایدار هستند. مثال زیر را در نظر بگیرید:

$$\dot{r} = (r^2-1)$$

$$\dot{\theta} = 1$$

در این سیستم حالت‌های سیستم تا $$r=1$$ همگرا می‌شوند، اما برای $$r>1$$، حالت‌ها به بی‌نهایت می‌روند.

بنابراین برخلاف سیستم‌های خطی، پایداری سیستم‌های غیر خطی به طبیعت غیر خطی بودن و حالت‌های سیستم بستگی دارد. پس روش‌های آنالیز مقادیر ویژه که برای سیستم‌های خطی بسط یافته بودند، دیگر مستقیما قابل استعمال نیستند. سه تکنیک برای تعیین پایداری سیستم به صورت زیر هستند:

1. حل معادلات دیفرانسیل به روش عددی (شبیه‌سازی) یا به روش تحلیلی و مطالعه رفتار جواب.
2. خطی‌سازی سیستم غیر خطی در تعدادی از نقاط و مطالعه رفتار آن‌ها. این روش مستعد خطای خطی‌سازی است.
3. تعریف یک تابع لیاپانوف و مطالعه رفتار خود تابع.

از بین تمام این روش‌ها، استفاده از تابع لیاپانوف دارای بیشترین دقت و کاربرد است و در برای آنالیز رفتار یک سیستم غیر خطی بیشتر از این روش استفاده می‌شود.

روش لیاپانوف برای آنالیز پایداری سیستم غیر خطی

در روش لیاپانوف، یک تابع مثبت معین (Positive-Definite) $$L$$ را تعریف می‌کنیم. از این تابع نسبت به زمان مشتق می‌گیریم و رفتار آن را بررسی خواهیم کرد. توجه کنید که این تابع را به نحوی تعریف می‌کنیم که در نقطه پایداری مورد تحقیق دارای مقدار صفر باشد. روش لیاپانوف می‌تواند به صورت زیر تعریف شود:

1. ابتدا تابع $$L$$ را به نحوی تعریف می‌کنیم که در تمام نقاط فضا به غیر از نقطه تعادل مثبت معین باشد.
2. مشتق این تابع را نسبت به زمان محاسبه می‌کنیم و کنترل می‌کنیم که تابع دارای کدام‌یک از مشخصه‌های زیر است:
   • اگر مشتق این تابع همواره منفی باشد، آن‌گاه حالت‌ها به صورت مجانبی (Asymptotically) به نقطه تعادل میل خواهند کرد.
   • اگر مشتق این تابع برای تمام $$X>a$$ به ازای یک $$a$$ معین منفی شود، آن‌گاه $$a$$ نشان‌دهنده مرز پایداری است. به عبارتی دیگر، بعد از زمان بی‌نهایت حالت‌های سیستم توسط $$a$$ برای همیشه محدود می‌شوند.

روش لیاپانوف برای سیستم‌های پیوسته در زمان

حال از روش لیاپانوف برای مطالعه رفتار یک سیستم گسسته در زمان مانند یک نوسان‌ساز وندر پل استفاده می‌کنیم. سیستم زیر را در نظر بگیرید:

$$\dot{X_1} = X_2$$

$$\dot{X_2} = \mu (1- X_1^2) X_2 - X_1$$

تابع لیاپانوفی را به صورت زیر در نظر می گیریم:

$$L(X_1,X_2) = \frac{1}{2} X_1^T X_1 + \frac{1}{2} X_2^T X_2$$

حال از این معادله نسبت به زمان مشتق می‌گیریم:

$$\frac{ \partial L }{ \partial t} = X_1^T \dot{X}_1 + X_2^T \dot{X}_2$$

با جایگذاری معادلات حالت در مشتق لیاپانوف داریم:

$$\frac{ \partial L }{ \partial t} = X_1^T X_2 + X_2^T \left( \mu (1- X_1^2) X_2 - X_1 \right)$$

$$\frac{ \partial L }{ \partial t} = \mu X_2^T (1- X_1^2) X_2$$

توجه کنید که $$\mu=0$$ یک حالت خاص است که در آن تابع لیاپانوف تغییری نمی‌کند و سیستم یک حرکت تناوبی ثابت را از خود نشان می‌دهد. بنابراین بر روی دو حالت دیگر یعنی $$\mu >0$$ و $$\mu < 0$$ تمرکز می‌کنیم:

حالت $$\mu > 0$$

در این حالت به سادگی $$\mu$$ را با قدر مطلق آن جایگزین می‌کنیم. زیرا باعث هیچ تغییری در رفتار سیستم نخواهد شد:

$$\frac{ \partial L }{ \partial t} = |\mu| X_2^T (1- X_1^2) X_2$$

بنابراین اگر $$1 - X_1^2 < 0$$، تابع لیاپانوف کاهش خواهد یافت. پس متغیرهای حالت همیشه محدود خواهند ماند و اگر $$(1 - X_1^2) > 0$$، حالت‌های سیستم به سمت $$X_1^2 = 1$$ خواهند رفت.

حالت $$\mu < 0$$

در این حالت $$\mu$$ را با منفی قدر مطلق آن جایگزین خواهیم کرد. زیرا منجر به تغییر رفتار سیستم نخواهد شد. تابع لیاپانوف به صورت زیر در خواهد آمد:

$$\frac{ \partial L }{ \partial t} = - |\mu| X_2^T (1- X_1^2) X_2$$

بنابراین اگر $$(1 - X_1^2) > 0$$ باشد، حالت‌های سیستم به صفر همگرا خواهند شد و اگر $$(1 - X_1^2) < 0$$ حالت‌های سیستم به بی‌نهایت خواهند رفت.

بنابراین با استفاده از روش لیاپانوف توانستیم رفتار سیستم را برای مقادیر پارامترها و حالت‌های مختلف توصیف کنیم.

نکته: برای سیستم‌های گسسته در زمان، تابع لیاپانوف مشابه با سیستم‌های پیوسته تعریف می‌شود، اما پایداری به وسیله تفاضل بین مقدار تابع لیاپانوف در لحظه حال و لحظه قبل به دست می‌آید.

کدهای زیر نوسان‌ساز وندر پل را به ازای $$\mu=1$$ رسم می‌کند:

شکل زیر پرتره فاز سیستم را نشان می‌دهد.

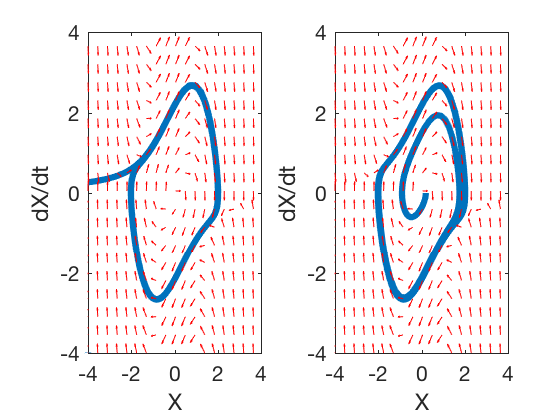
کد زیر نیز پرتره فاز را برای $$\mu=-1$$ رسم خواهد کرد.

شکل زیر پرتره فاز در این حالت را نشان می‌دهد.

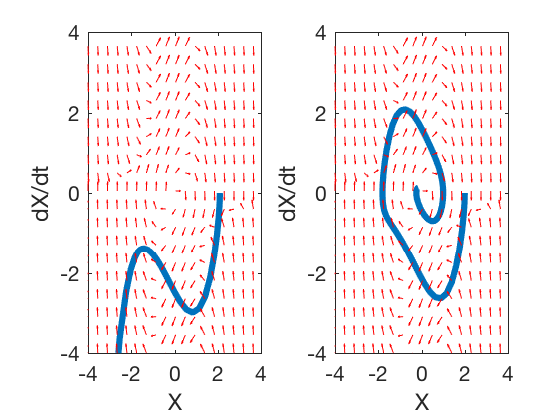
اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی کنترل
• آموزش طراحی سیستم های کنترل غیر خطی
• مجموعه آموزش مهندسی برق
• آموزش کنترل صنعتی – حل مساله
• خطی سازی سیستم های غیر خطی — از صفر تا صد
• کنترل کننده PID — مفاهیم و ساختارها

^^