تقسیم عدد صحیح – به زبان ساده

در ریاضیات، یکی از مفاهیم و عملگر‌های چهار عمل اصلی، تقسیم (Division) است. اغلب برای بخش‌پذیری و بدست آوردن سهم یک شئ از تقسیم عدد صحیح کمک می‌گیریم. برای مثال وقتی می‌خواهیم سیبی را نصف کنیم یا بخشی از پولمان را برای خرید لوازم‌التحریر اختصاص دهیم، از تقسیم کردن استفاده می‌کنیم. در این نوشتار به بررسی نحوه تقسیم عدد صحیح پرداخته و شیوه و روند انجام عملیات تقسیم را فرا می‌گیریم. البته برای آشنایی بیشتر با مفهوم بخش‌پذیری بهتر است ابتدا مطلب بخش پذیری در اعداد — به زبان ساده را بخوانید. همچنین خواندن نوشتار اعداد گویا — به زبان ساده نیز  خالی از لطف نیست.

روش ارائه شده در این نوشتار، تقسیم عدد صحیح با روش «تقسیم اقلیدسی» (Euclidean Division) است و در آن خارج قسمت و باقی‌مانده هر دو از مجموعه اعداد صحیح خواهند بود. این روش که براساس ضرب و تفاضل‌های تکراری برای تقسیم به کار می‌رود، اغلب برای انجام عمل تقسیم در رایانه‌ها و برنامه‌های محاسباتی ساده به کار گرفته می‌شود. ولی تکنیک‌های دیگر مانند روش نیوتن رافسون برای تقسیم‌های اعشاری کارآمدتر هستند. یکی از قضیه‌های مهم در تقسیم کردن اعداد صحیح، یکتا بودن (Uniqueness) جواب یعنی خارج قسمت و باقی مانده است که پاسخ تقسیم را به روشنی مشخص می‌کنند.

از کاربردهای مهم تقسیم عدد صحیح، می‌توان عاد کردن یا تعیین تعداد شمارنده‌های یک عدد را در نظر گرفت. در نوشته‌های دیگر فرادرس در مورد تعیین شمارنده و تعداد آن‌ها برای اعداد طبیعی (صحیح) صحبت خواهیم کرد.

تقسیم عدد صحیح

برعکس عمل ضرب اعداد، عمل تقسیم کمی پیچیده‌ به نظر می‌رسد. از آنجایی که تقسیم عدد صحیح ساده‌تر است ابتدا روش تقسیم را در این مجموعه جستجو می‌کنیم.

در ابتدا اعدادی که مربوط به مجموعه اعداد صحیح هستند را در نظر گرفته و تقسیم کردن اعداد صحیح را مرور می‌کنیم سپس در نوشتارهای بعدی به نحوه تقسیم اعداد حقیقی خواهیم پرداخت.

همانطور که می‌دانید، اعضای مجموعه اعداد طبیعی به صورت زیر نوشته می‌شوند. نام $$N$$ به علت حرف اولی Natural یا طبیعی برای این مجموعه اعداد در نظر گرفته شده است.

$$\large N=\{1,2,3,\ldots\}$$

عدد صفر و مقادیر منفی در این مجموعه اعداد جایی ندارند. این مجموعه برای شمارش اشیائی که در طبیعت وجود دارند، مناسب است به همین دلیل این مجموعه را طبیعی نامیده‌اند.

از طرفی ممکن است که اعداد، دارای جهت نیز باشند که با علامت مثبت یا منفی مشخص می‌شوند. این مجموعه اعداد را به نام اعداد صحیح می‌شناسیم و با حرف $$Z$$ نشان می‌دهیم. در این حالت داریم:

$$\large Z=\{\ldots,-3,-2,-1,0,1,2,3,\ldots\}$$

همانطور که مشخص است، از هر دو جهت، این مجموعه اعداد، بی‌کران و نامحدود است. معمولا برای نمایش اعداد صحیح از دو بردار جهت دار که در امتداد یکدیگر قرار داشته و در نقطه صفر مشترک هستند استفاده می‌شود.

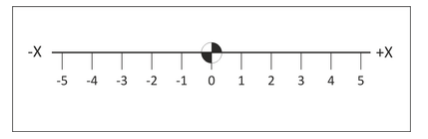
حال فرض کنید در مجموعه اعداد طبیعی یا صحیح گام بر‌می‌داریم. پس اگر $$a$$، $$b$$، $$c$$ اعدادی از این مجموعه باشند، آنگاه ممکن است رابطه ۱ بین آن‌ها قابل بررسی باشد.

$$\large a = b\times c$$

رابطه ۱

در صورتی که این اعداد در رابطه ۱ صدق کنند، در این صورت می‌توانیم منظور از تقسیم $$a$$ بر $$b$$ را پیدا کردن عددی مثل $$c$$ بدانیم که رابطه ۱ برایشان صادق است. در این حال می‌نویسیم:

$$\large a\div b = c$$

رابطه ۲

در این صورت $$a$$‌ را مقسوم، $$b$$ را مقسوم علیه و $$c$$ را خارج قسمت تقسیم می‌نامیم. در نظر داشته باشید که در اینجا $$b$$ و $$c$$ کوچکتر از $$a$$ هستند.

نکته: توجه داشته باشید که در اینجا $$b$$ باید مخالف صفر باشد زیر از نظر بسیاری از ریاضیدان‌ها، تقسیم عدد بر صفر تعریف نشده یا بی‌معنا است.

برای مثال اگر $$a=10$$ و $$b=5$$ باشد، آنگاه رابطه 2 مطابق با فرمول زیر نوشته خواهد شد.

$$\large 10\div 5 = 2$$

زیرا

$$\large 10=5\times 2$$

در این حالت می‌گوییم، اگر ۱۰ را به ۵ تقسیم کنیم، خارج قسمت برابر با ۲ است.

بنابراین هنگامی که برای اعداد بخواهیم تقسیم را انجام دهیم، شاید استفاده از عمل ضرب مطابق با رابطه 1 مناسب باشد. ولی همیشه نمی‌توان به سرعت و راحتی، عدد $$c$$ را مشخص کرد.

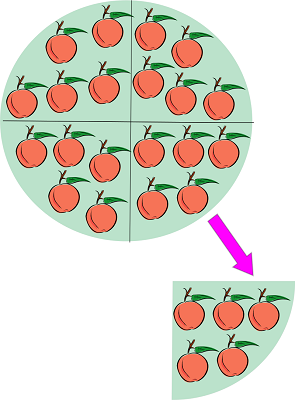
به تصویر بالا دقت کنید، در اینجا ۲۰ سیب به دسته‌های پنج‌تایی تقسیم شده است. حاصل این تقسیم برابر است با ۴ زیرا ۲۰ سیب را می‌توان به چهار دسته پنج‌تایی تقسیم کرد. به این ترتیب داریم:

$$\large 20\div 5 =4$$

زیرا

$$\large 20=5\times 4$$

این عبارت را می‌توان به صورت دیگری نیز خواند یا تفسیر کرد. اگر بخواهیم ۲۰ سیب را به چهار دسته تقسیم کنیم، در هر دسته ۵ سیب قرار می‌گیرد. در این حالت خواهیم داشت:

$$\large 20\div 4 = 5$$

زیرا

$$\large 20=4\times 5$$

از آنجایی که ضرب دارای خاصیت جابجایی است می‌توان با جابجا کردن مقسوم علیه و خارج قسمت با یکدیگر، رابطه ضربی یکسانی نوشت. در نتیجه خواهیم داشت:

$$\large 20\div 4 = 5$$ و  $$\large 20\div 5 = 4$$

زیرا

$$\large 20=4\times 5= 5 \times 4 = 20$$

مراحل انجام عملیات تقسیم عدد صحیح و محاسبه خارج قسمت

برای انجام عملیات تقسیم می‌توانیم گام‌هایی را به صورت متوالی انجام دهیم تا به نتیجه یا حاصل تقسیم که همان خارج قسمت است برسیم. این کار بوسیله روش ضرب‌ و تفاضل‌های متوالی صورت می‌گیرد.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

در ادامه با ذکر مثال‌هایی به این موضوع می‌پردازیم و شیوه اجرای تقسیم را مورد بررسی قرار می‌دهیم. ابتدا گام‌ها را مشخص می‌کنیم.

1. مقسوم علیه را در اولین و دومین عدد طبیعی (یا صحیح) غیر از صفر ضرب می‌کنیم.
2. اگر حاصل ضرب اولی کوچکتر یا مساوی با مقسوم و دومی نیز بزرگتر از مقسوم بود، می‌توان نتیجه گرفت که خارج قسمت، همان عدد اولی است.
3. اگر شرط مربوط به گام دوم محقق نشد، به هر یک از اعداد قبلی، یک واحد اضافه می‌کنیم و عمل ضرب هر یک از آن‌ها در مقسوم علیه انجام می‌دهیم.
4. عملیات را از گام دوم دوباره اجرا می‌کنیم.

برای روشن شدن موضوع به ذکر دو مثال می‌پردازیم.

مثال 1: فرض کنید که $$a=15$$  و $$b=5$$ باشد. راه حلی که در بالا به آن اشاره کردیم برای تقسیم $$15$$ بر $$5$$ به کار می‌بریم.

• 5 را در 1 و 2 ضرب می‌کنیم. حاصل اولی برابر با $$5 \times 1=5$$ و دومی هم $$5\times 2=10$$ شده است.
• از آنجایی که هر دو مقدار حاصل شده از گام اول از مقسوم یعنی 15 کوچکتر هستند، عمل ضرب را با اعداد بزرگتر ادامه می‌دهیم. به هر یک از مقادیر یک واحد اضافه می‌کنیم تا مقدارهای 2 و 3 حاصل شود.
• 5 را در 2 و 3 ضرب می‌کنیم. از آنجایی که نتیجه اولی برابر با $$5\times2=10$$ و دومی $$5\times 3=15$$ شده، شرط مربوط به گام دوم در الگوریتم بالا محقق نشده است. پس به هر یک واحد اضافه می‌کنیم.
• 5 را در 3 و 4 ضرب می‌کنیم. از آنجایی که نتیجه اولی برابر با $$5\times3=15$$ و دومی $$5\times 4=20$$ شده، شرط مربوط به گام دوم در الگوریتم بالا محقق شده است پس عملیات تقسیم متوقف می‌شود.
• مقدار ۳ خارج قسمت خواهد بود.

مثال 2: فرض کنید $$a=10$$ و $$b=4$$ باشد. عمل تقسیم را به کمک روند و مراحلی که در ادامه مشخص شده است، تعیین می‌کنیم.

به این ترتیب مراحل را به صورت زیر برای تقسیم 10 بر ۴ انجام می‌دهیم. واضح است که در اینجا ۱0 مقسوم و ۴ مقسوم علیه است.

• 4 را در 2 و 3 ضرب می‌کنیم. حاصل اولی برابر با $$4 \times 1=4$$ و دومی هم $$4\times 2=8$$ شده است.
• از آنجایی که هر دو مقدار حاصل شده از گام اول از مقسوم یعنی 10 کوچکتر هستند، عمل ضرب را با اعداد بزرگتر ادامه می‌دهیم. به هر یک از مقادیر ۱ و ۲، یک واحد اضافه می‌کنیم.
• ۴ را در ۲ و ۳ ضرب می‌کنیم. از آنجایی که نتیجه اولی برابر با $$4\times2=8$$ و دومی $$4\times 3=12$$ شده، شرط مربوط به گام دوم در الگوریتم بالا محقق شده است. پس عملیات تقسیم متوقف می‌شود.
• مقدار اولی یعنی ۲ خارج قسمت خواهد بود.

نکته: گاهی ممکن است با اجرای این عملیات و ضرب‌ها و مقایسه‌ها به مقدار دقیق مقسوم نرسیم، در نتیجه به نظر می‌رسد که این تقسیم می‌تواند به شکل دیگری هم ادامه داشته باشد و عملیات تقسیم شامل باقی‌مانده هم باشد.

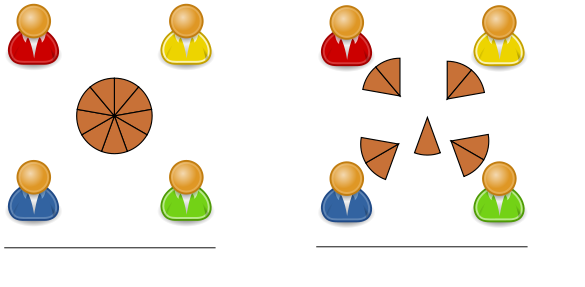
تقسیم عدد صحیح همراه با باقیمانده

همانطور که گفته شد، همیشه با ضرب کردن اعداد صحیح در مقدار مقسوم علیه، به مقسوم نمی‌رسیم. در اینجا موضوع یا مفهوم باقی‌مانده در تقسیم بوجود می‌آید. فرض کنید رابطه زیر بین چهار عدد $$a$$، $$b$$, $$c$$ و $$d$$ وجود داشته باشد.

$$\large a=b\times c+d$$

در این حالت $$d$$ را باقی‌مانده تقسیم $$a$$ بر $$b$$ می‌نامیم. به این ترتیب می‌توان نوشت:

$$\large a \div b = c+\dfrac{d}{b}$$

توجه داشته باشید که در اینجا هم شرطی برای باقیمانده وجود دارد. در حقیقت اگر تقسیم عدد صحیح به درستی انجام شده باشد، باقیمانده باید از خارج قسمت کوچکتر و همیشه مثبت باشد. در این صورت مراحل انجام تقسیم پایان یافته است.

برای پیدا کردن باقی‌مانده یک تقسیم، کافی است مراحل گفته شده برای تقسیم را طی کنیم و در آخرین مرحله حاصل ضرب مقسوم علیه در خارج قسمت را از مقسوم کم کنیم. این رابطه به صورت زیر نوشته می‌شود.

$$\large d= a-b\times c$$

اغلب در ریاضیات برای نمایش باقی‌مانده از حرف $$r$$ که مخفف Reminder است استفاده می‌کنند. همچنین خارج قسمت تقسیم نیز با حرف $$q$$ نشان داده می‌شود که مخفف Quotient است. در نتیجه داریم:

$$\large a=b\times q+d , \;\;\;\;r= a-b\times q , \;\;\;a \div b = q+\dfrac{r}{b}$$

در اینجا هم باید شرط $$r\geq 0$$ و $$r\leq q$$ وجود داشته باشد.

تقسیم عدد صحیح چند رقمی

با روشی که برای انجام عمل تقسیم در قسمت قبل گفتیم، انجام مراحل برای اعداد بزرگ به راحتی صورت نخواهد گرفت ولی می‌توانیم از مفاهیمی که برای تقسیم اعداد تک رقمی در قسمت قبل فراگرفتیم، استفاده کنیم. مراحل انجام عملیات را باز هم به کمک مثال‌هایی در این زمینه تعیین می‌کنیم.

برای پاسخ به این پرسش، از گام‌های مربوط به تقسیم دو عدد استفاده می‌کنیم ولی این کار را به صورت تکراری برای هر قسمت از مقسوم انجام خواهیم داد و در حاصل خارج قسمت و باقی‌مانده را محاسبه می‌کنیم. گام‌های مربوط به تقسیم کردن اعداد صحیح همراه با باقی‌مانده در ادامه مشخص شده‌اند.

1. به تعداد ارقام مقسوم علیه از از سمت چپ مقسوم،‌ ارقام را جدا می‌کنیم و آن را مقسوم جدید در نظر می‌گیریم.
2. اگر تقسیم امکان پذیر نبود یعنی مقسوم جدید از مقسوم علیه کوچکتر بود، رقم‌های بعدی از سمت چپ را یکی یکی به مقسوم جدید اضافه کرده تا عمل تقسیم امکان‌پذیر باشد.
3. عمل تقسیم مقسوم جدید را بر مقسوم علیه انجام می‌دهیم و خارج قسمت را محاسبه می‌کنیم. خارج قسمت هر مرحله را در سمت راست خارج قسمت مرحله قبلی قرار می‌دهیم.
4. با ضرب خارج قسمت در مقسوم علیه و کسر نتیجه حاصل ضرب از مقسوم اولیه، باقی‌مانده را محاسبه می‌کنیم.
5. باقی‌مانده به همراه ارقام استفاده نشده از مقسوم اولیه را از چپ به راست در کنار یکدیگر چیده و به عنوان مقسوم جدید در نظر می‌گیریم.
6. اگر شرایط تقسیم وجود نداشته باشد (یعنی باقی‌مانده یا همان مقسوم جدید از مقسوم علیه کوچکتر باشد)، مراحل تقسیم را متوقف کرده، باقی‌مانده و خارج قسمت را مشخص می‌کنیم.
7. در غیر اینصورت گام‌های تقسیم را از مرحله ۱ تکرار می‌کنیم.

مثال ۳: حاصل تقسیم 124 بر ۴ چیست؟

مشخص است که تعداد ارقام مقسوم و مقسوم علیه برای اجرای مراحل تقسیم مهم است. همانطور که دیده می‌شود مقسوم ۳ رقم و مقسوم علیه یک رقمی است. گام‌های گفته شده در بالا را به کار می‌گیریم.

• به نظر می‌رسد با انتخاب یک رقم از سمت چپ عدد ۱۲۴، عمل تقسیم بر ۴ امکان‌پذیر نیست. بنابراین ۲ رقم را انتخاب می‌کنیم.
• می‌دانیم که ۱۲ تقسیم بر ۴، خارج قسمتی برابر با ۳ و باقی‌مانده صفر خواهد داشت. خارج قسمت برابر با ۳ است.
• حال باقی‌مانده را براساس خارج قسمت جدید محاسبه می‌کنیم که برابر با ۴ است. این باقی‌مانده را به عنوان مقسوم جدید در نظر می‌گیریم. از آنجایی که باقی‌مانده از مقسوم علیه کوچکتر نیست، عملیات تقسیم ادامه پیدا می‌کند.
• به تعداد یک رقم از سمت چپ مقسوم جدید جدا می‌کنیم. حاصل برابر با ۴ است که خارج قسمت تقسیم آن بر مقسوم علیه (یعنی ۴) برابر با ۱ است. واضح است که باقی‌مانده هم صفر خواهد بود.
• با کنار هم قرار دادن خارج قسمت‌ها از چپ به راست برای گام‌های طی شده، خارج قسمت برابر با ۳۱ خواهد بود از طرفی، باقی‌مانده هم صفر است.

این گام‌ها توسط تصویر زیر نمایش داده شده‌اند.

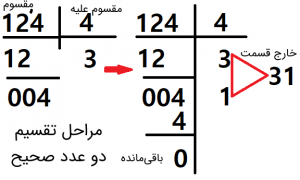
همانطور که دیده می‌شود باقی‌مانده صفر شده و براساس کنار هم قرار گرفتن خارج‌قسمت‌های مراحل مختلف، خارج قسمت تقسیم اصلی، ایجاد شده است.

مثال 4: حاصل تقسیم 825 بر 24 چیست؟

• با توجه به اینکه مقسوم سه رقمی و مقسوم علیه یعنی ۲۴ دو رقمی است، از سمت چپ ۸۲۵، دو رقم جدا می‌کنیم یعنی ۸۲ به عنوان مقسوم جدید در نظر گرفته می‌شود.
• تقسیم ۸۲ بر ۲۴ را انجام می‌دهیم. خارج قسمت برابر با ۳ خواهد شد. زیرا $$24\times 3=72$$ و $$24 \times 4= 84$$ که از ۸۲ بزرگتر است. پس خارج قسمت برابر با ۳ و باقی مانده نیز ۱۰ خواهد بود چون $$82-24\times 24=82-72=10$$.
• با قرار دادن باقی‌مانده با ارقام بعدی مقسوم، عدد ۱۰۵ حاصل می‌شود. حاصل تقسیم این مقسوم جدید بر ۲۴، نیز مقدار 4 خواهد بود. باقی مانده نیز برابر با 9 شده و چون 9 کوچکتر از ۲۴ است، مراحل تقسیم تمام خواهد شد.

این گام‌ها توسط تصویر زیر نمایش داده شده‌اند.

واضح است که در انتها، ارقام ایجاد شده برای خارج قسمت، به ترتیب از سمت چپ در کنار یکدیگر نوشته شده‌اند تا مقدار ۳4 به عنوان خارج قسمت ساخته شود. به این ترتیب تقسیم اعداد صحیح به کمک تقسیم و تفاضل‌های تکراری انجام می‌شود.

نکته: برای تقسیم عدد صحیح، منفی بر مثبت یا مثبت بر منفی و همچنین منفی بر منفی، از قواعد ضرب اعداد علامت دار استفاده می‌کنیم.

• در صورتی که مقسوم و مقسوم علیه هر دو مثبت باشند، خارج قسمت حتما مثبت است.
• اگر مقسوم مثبت و مقسوم علیه منفی باشد، خارج قسمت حتما منفی است.
• اگر مقسوم منفی و مقسوم علیه مثبت باشد، خارج قسمت منفی محاسبه می‌شود.
• در صورتی که مقسوم و مقسوم علیه هر دو منفی باشند، خارج قسمت حتما مثبت است.

باید به این نکته توجه داشت که در اینجا همیشه باقی‌مانده باید مثبت یا صفر باشد. برای مثال حالت‌های زیر را در نظر بگیرید:

• اگر $$a=7$$ و $$b=3$$ باشد، آنگاه $$q=2$$ و $$r=1$$ زیرا $$7 = 3\times (2) +1$$.
• اگر $$a=7$$ و $$b=-3$$ باشد، آنگاه $$q=-2$$ و $$r=1$$ زیرا $$7 = -3\times (-2) +1$$.
• اگر $$a=-7$$ و $$b=3$$ باشد، آنگاه $$q=-3$$ و $$r=2$$ زیرا $$-7 = 3\times (-3) +2$$.
• اگر $$a=-7$$ و $$b=-3$$ باشد، آنگاه $$q=3$$ و $$r=2$$ زیرا $$-7 = -3\times (3) +2$$.

جمع‌بندی و خلاصه

در این نوشتار، ابتدا با مفهوم تقسیم عدد صحیح آشنا شدیم و سپس نحوه محاسبه آن را برحسب ضرب و تفریق فرا گرفتیم. همچنین روندهای تکراری برای تقسیم عدد صحیح (بدون ارقام اعشار) را مشخص کردیم. در نوشتارهای بعدی نحوه ضرب و تقسیم اعشاری و تقسیم در کسرها را نیز مرور کرده و مورد بررسی قرار می‌دهیم.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های ریاضی و فیزیک
• آموزش جامع ریاضی دبیرستان – علوم تجربی
• اعداد حقیقی — به زبان ساده
• اعداد گویا — به زبان ساده
• اعداد مختلط – به زبان ساده