تفریق اعداد مخلوط – به زبان ساده + حل تمرین
در آموزشهای پیشین مجله فرادرس، با اعداد مخلوط و جمع اعداد مخلوط آشنا شدیم. در این آموزش، روشهای محاسبه تفریق اعداد مخلوط را شرح میدهیم.
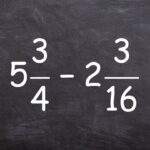
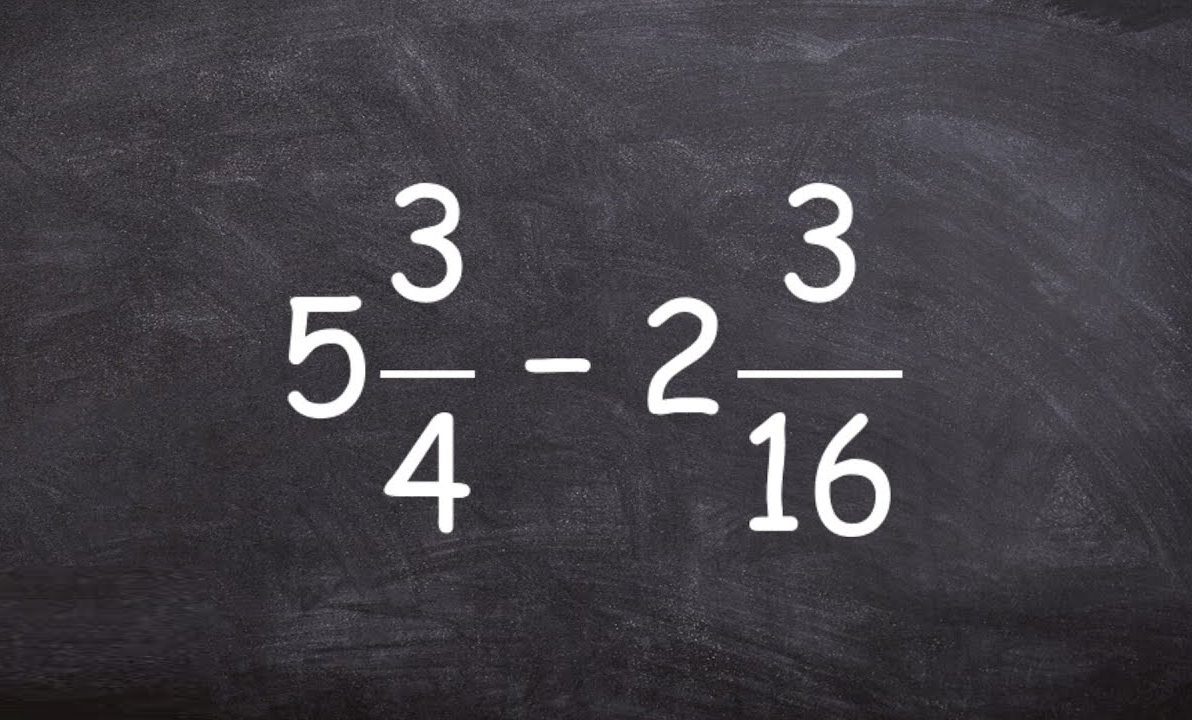
عدد مخلوط چیست؟
عدد مخلوط عددی است که از دو بخش تشکیل میشود: یک بخش آن عدد صحیح است و بخش دیگرش یک عدد کسری سره. منظور از کسر سره کسری است که مخرج آن از صورتش بزرگتر باشد. اعداد زیر عدد مخلوط هستند:
روشهای تفریق اعداد مخلوط
با توجه به نوع و چگونگی دو عدد مخلوطی که میخواهیم تفریق بین آنها را انجام دهیم، میتوان از روشهای مختلفی برای تفریق استفاده کرد. دو حالت وجود دارد که ممکن است با آنها مواجه شویم:
- مخرج کسرهای دو عدد یکسان باشند.
- مخرج کسرهای دو عدد متفاوت باشند.
تفریق اعداد مخلوط با مخرج یکسان
در حالتی که مخرج دو عدد مخلوط یکی باشد، بهراحتی میتوانیم تفریق را از دو راه انجام دهیم.
تفریق دو عدد مخلوط با تفریق جداگانه عدد صحیح و کسری
یکی از روشها این است که ابتدا تفریق اعداد صحیح را انجام دهیم، سپس تفریق کسرها را. مثال زیر این روش را بهخوبی روشن میکند.
میخواهیم حاصل تفریق را محاسبه کنیم. ابتدا دو عدد صحیح را از هم کم میکنیم:
در ادامه، تفریق دو عدد کسری را انجام میدهیم:
بنابراین، جواب برابر است با
تفریق دو عدد مخلوط با تبدیل به کسر
در این روش، ابتدا دو عدد مخلوط را به کسر تبدیل میکنیم، سپس تفریق را انجام میدهیم. در نهایت نیز عدد بهدستآمده را به عدد مخلوط تبدیل میکنیم.
برای مثال، میخواهیم حاصل را بهدست آوریم. ابتدا دو عدد را به کسر تبدیل میکنیم، سپس تفریق را انجام میدهیم:
در نهایت، عدد کسری را در صورت امکان به عدد مخلوط تبدیل میکنیم:
نکته: ممکن است این پرسش برایتان پیش آمده باشد که دلیل معرفی روش دوم چیست، زیرا همانطور که مشخص است، نسبت به روش اول بیشتر طول میکشد. گاهی پیش میآید که کسر عدد مخلوط اول از کسر عدد مخلوط دوم کوچکتر است. در چنین مواردی، برای آنکه دچار سردرگمی نشویم، از روش دوم استفاده میکنیم.
برای مثال، فرض کنید میخواهیم تفریق را انجام دهیم. اعداد صحیح را میتوان بهسادگی از هم کم کرد، اما برای تفریق بخش کسری به مشکل برمیخوریم، زیرا از کوچکتر است. اینجاست که از روش دوم استفاده میکنیم و در ابتدا دو عدد مخلوط را به کسر تبدیل میکنیم:
اکنون یک تفریق بین دو کسر داریم و بهسادگی میتوانیم آن را انجام دهیم:
اکنون میتوانیم این عدد کسری را بهشکل یک عدد مخلوط بنویسیم:
تفریق اعداد مخلوط با مخرج نامساوی
اگر مخرج بخش کسری دو عدد یکسان نباشد، یک مرحله به مراحل بخش قبل اضافه میشود و آن این است که باید مخرج مشترک بگیریم. اینجا هم دو روش داریم.
تفریق دو عدد مخلوط با تفریق جداگانه عدد صحیح و کسری
در این روش، اعداد صحیح را جداگانه، و اعداد کسری را نیز جداگانه از هم کم میکنیم.
برای مثال، میخواهیم تفریق را انجام دهیم. برای این کار، ابتدا دو عدد صحیح را از هم کم میکنیم:
حاصل تفریق دو بخش کسری با کمک مخرج مشترک گرفتن، بهصورت زیر بهدست میآید:
اکنون حاصل تفریق بخش صحیح و بخش کسری را در کنار یکدیگر قرار میدهیم. جواب نهایی بهصورت زیر است:
تفریق عدد مخلوط و عدد کسری
تفریق عدد مخلوط و عدد کسری مشابه آنچه است که در بخشهای قبل بیان کردیم. در این حالت نیز میتوان از دو روش استفاده کرد.
روش اول: در روش اول، میتوانیم عدد مخلوط را به کسر تبدیل کنیم. فرض کنید میخواهیم تفریق را انجام دهیم. در این صورت، باید تفریق دو کسر را انجام دهیم:
از آنجا که مخرجها در این مثال یکسان نیست، باید مخرج مشترک نیز بگیریم و حاصل را بهدست آوریم:
در نهایت، میتوانیم عدد کسری را به عدد مخلوط تبدیل کنیم:
روش دوم: روش قبلی یک روش کلی است که برای حالتهای مختلف قابل اعمال است. در حالت خاصی که عدد کسری را از عدد مخلوط کم کنیم، میتوانیم عدد صحیح مربوط به عدد مخلوط را بنویسیم و کسر را از کسر عدد مخلوط کم کنیم. با یک مثال، این روش را توضیح میدهیم. فرض کنید میخواهیم تفریق را انجام دهیم. برای این کار، عدد صحیح مربوط به عدد مخلوط را مینویسیم، سپس تفاضل اعداد کسری را مینویسیم:
چون مخرجها تفاوت دارند، باید مخرج مشترک بگیریم:
بنابراین، جواب نهایی بهصورت زیر است:
تفریق عدد مخلوط و عدد صحیح
تفریق اعداد مخلوط و صحیح بهآسانی قابل انجام است. چند مثال زیر، سادگی این کار را نشان میدهند:
تفریق اعداد مخلوط با کمک شکل
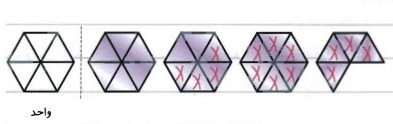
برای انجام تفریق اعداد مخلوط با کمک شکل، ابتدا باید شکل متناظر با عدد نخست را رسم کنیم. برای این کار، به یک واحد کامل یک شکل کامل اختصاص میدهیم. سپس این شکل واحد را بر اساس مخرج کسر مربوط به آن، به قسمتهای مساوی تقسیم میکنیم. مثلاً اگر عدد را داشته باشیم، باید شکل را به شش قسمت مساوی تقسیم کنیم. برای نشان دادن عدد، سه واحد کامل برای عدد و تکه از تکه یک شکل را قرار میدهیم. برای انجام تفریق، باید عدد دوم را از عدد اول که نمایش دادهایم، کم کنیم. برای این کار باید معادل عدد دوم، از عدد اول حذف کنیم. برای مثال، فرض کنید میخواهیم تفریق را با کمک شکل انجام دهیم. در این صورت باید دو شکل کامل و دو تکه از یک شکل را حذف کنیم. آنچه باقی میماند، حاصل تفریق است.
شکل زیر این موضوع را بهخوبی نشان میدهد. معادل عدد دوم را با علامت ضربدر خط زدهایم و آنچه از کل شکل باقی مانده، یک واحد شکل کامل و دو تکه از شش تکه است، یعنی عدد .
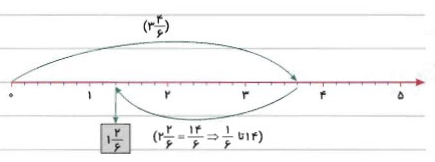
تفریق اعداد مخلوط روی محور اعداد
این روش را با یک مثال شرح میدهیم. فرض کنید میخواهیم تفریق را انجام دهیم. ابتدا عدد مخلوط را روی محور مشخص میکنیم. برای این کار، هر واحد را باید به شش بخش تقسیم کنیم، زیرا مخرج کسر عدد است. در ادامه، از نقطه انتهای کمان مربوط به عدد نخست، بهاندازه عدد دوم برگردیم. برای این کار، ابتدا این عدد را به کسر تبدیل میکنیم: . بنابراین، باید خانه کوچک به عقب برگردیم. نقطهای که به آن میرسیم، جواب تفریق است. از نقطه صفر تا آن نقطه میشماریم. میبینیم که آن نقطه است.
مثالهای تفریق اعداد مخلوط
در این بخش، چند مثال را از تفریق اعداد مخلوط بررسی میکنیم.
مثال اول تفریق اعداد مخلوط
حاصل تفریق را محاسبه کنید.
حل: برای بهدست آوردن جواب، اعداد صحیح را جدا، و اعداد کسری را جدا از هم کم میکنیم:
میبینیم که دو عدد کسری، مخرج یکسانی ندارند. بنابراین، باید مخرج مشترک بگیریم و آن دو را از هم کم کنیم. ک.م.م دو عدد و ، عدد است که مخرج مشترک دو کسر میشود. مراحل زیر، نحوه محاسبه جواب نهایی را نشان میدهند:
مثال دوم تفریق اعداد مخلوط
تفریق حاصل را محاسبه کنید.
حل: مطابق آنچه پیشتر نیز انجام دادیم، اعداد صحیح را جدا و کسرها را جدا با هم جمع میکنیم. چون مخرج کسرها (اعداد و ) یکسان نیستند، باید مخرج مشترک بگیریم. مخرج مشترک عدد است. در نتیجه، خواهیم داشت:
مثال سوم تفریق اعداد مخلوط
تفریق را محاسبه کنید.
حل: این مثال را با روش دیگری حل میکنیم. بهجای آنکه اعداد صحیح را جدا و کسرها را جدا تفریق کنیم، ابتدا اعداد مخلوط را به کسر تبدیل و سپس تفریقشان میکنیم. مخرج مشترک دو کسر است. جواب بهشکل زیر محاسبه میشود:
مثال چهارم تفریق اعداد مخلوط
حاصل تفریق چه عددی است؟
حل: عدد صحیح مربوط به عدد مخلوط اول، است و عدد صحیح مربوط به عدد مخلوط دوم، عدد . تفاضل این دو برابر است با
عدد کسری عدد مخلوط اول است و عدد کسری عدد مخلوط دوم، . تفاضل این دو برابر است با
اکنون که بخش صحیح و بخش کسری را جداکانه تفریق کردهایم، آنها را در کنار هم میآوریم و جواب نهایی را مینویسیم:
مثال پنجم تفریق اعداد مخلوط
حاصل تفریق را محاسبه کنید.
حل: ابتدا دو عدد را به عدد کسری تبدیل میکنیم، سپس مخرج مشترک میگیریم:
و جواب برابر است با
جمعبندی
در این آموزش، با روش تفریق اعداد مخلوط برای حالتهای مختلف آشنا شدیم. دیدیم که با کمک شکل و محور اعداد میتوان تفریق این اعداد را محاسبه کرد. همچنین، روشهای دیگری را همراه با حل مثال برای محاسبه تفریق دو عدد مخلوط بیان کردیم.
آزمون تفریق اعداد مخلوط
۱. کدام جمله درباره عدد مخلوط درست است؟
عدد مخلوط ترکیبی از یک عدد صحیح و یک کسر است.
عدد مخلوط فقط یک عدد صحیح است که بخش کسری ندارد.
عدد مخلوط ترکیبی از دو کسر با مخرج برابر است.
عدد مخلوط جمع دو عدد صحیح بدون کسر است.
عدد مخلوط ترکیبی از یک عدد صحیح و یک کسر است.
۲. در تفریق دو عدد مخلوط با مخرج یکسان، چرا جدا کردن بخش صحیح و بخش کسری هر عدد اهمیت دارد؟
کمک میکند که همیشه نتیجه به صورت عدد صحیح باشد.
این کار باعث میشود عملیات سادهتر و سریعتر انجام شود.
برای تبدیل اعداد مخلوط به کسر لازم است.
فقط هنگام داشتن مخرجهای متفاوت کاربرد دارد.
زمانی که مخرج کسرهای دو عدد مخلوط برابر باشد، جدا کردن بخش صحیح از بخش کسری باعث میشود محاسبه راحتتر شود و ابتدا اعداد صحیح و سپس کسرها به سادگی از هم کم شوند. این روش نیاز به تبدیل اعداد به اشکال پیچیده یا کسر ندارد و محاسبه را برای همه قابل فهم و سریع میکند.
۳. در تفریق کسر از یک عدد مخلوط، چه زمانی بهتر است عدد مخلوط را به کسر تبدیل کنیم؟
وقتی جمع دو عدد از ده بیشتر شود.
هر وقت اعداد صحیح دو عدد مساوی باشد.
هر بار که مخرجها با هم برابر نباشند.
زمانی که بخش کسری عدد مخلوط از مقدار کسر کوچکتر باشد.
تبدیل عدد مخلوط به کسر زمانی توصیه میشود که بخش کسری عدد مخلوط از مقدار کسر کوچکتر باشد، زیرا در این حالت کمکردن مستقیم ممکن نیست و تبدیل به کسر سادهتر عمل تفریق را ممکن میسازد.
۴. هنگام تفریق دو عدد مخلوط با مخرج کسر متفاوت، کدام ترتیب کلی باید رعایت شود؟
فقط قسمت کسری را با مخرج مشترک کنید و بخش صحیح را تغییر ندهید.
هر دو عدد مخلوط را به کسر تبدیل کنید و مستقیما کم کنید.
ابتدا مخرج مشترک برای کسرها بگیرید، سپس بخش صحیح را کم کنید و نهایتا کسرها را نیز کم کنید.
ابتدا بخش صحیح را کم کنید، سپس کسرها را بدون تغییر مخرج کم کنید.
وقتی دو عدد مخلوط با مخرج متفاوت باید کم شوند، اول باید کسرها مخرج مشترک پیدا کنند تا تفریق ممکن باشد. سپس بخش صحیح کم میشود و در نهایت کسرهای با مخرج مشترک کم میشوند. اگر مخرج مشترک گرفته نشود یا صرفا اعداد مخلوط به کسر تبدیل شوند، روش مخصوص حالتهای دیگر است و رویکرد اصلی اینجا نیست. نگه داشتن بخش صحیح بدون کمکردن یا حذف مرحله مخرج مشترک باعث اشتباه در نتیجه خواهد شد؛ فقط «ابتدا مخرج مشترک بگیرید، سپس بخش صحیح را کم کنید و نهایتا کسرها را کم کنید» ترتیب صحیح است.
۶. در روش تفریق اعداد مخلوط روی محور اعداد، چه کاری انجام میشود و چه فایدهای دارد؟
عدد مخلوط را به کسر نامتعارف تبدیل و تفریق میکنیم.
برای کم کردن فقط بخش صحیح، کسر را نادیده میگیریم.
عدد مخلوط را روی محور اعداد نمایش میدهیم و خانهها را برای کمکردن به عقب میشماریم.
هر جزء عدد مخلوط را جداگانه زیر هم نوشته و کم میکنیم.
در روش نمایش تفریق اعداد مخلوط بر روی محور اعداد ابتدا عدد مخلوط مطابق بخشهای صحیح و کسری روی محور قرار میگیرد و سپس با شمردن خانهها به عقب، مقدار مورد نظر کاسته میشود. این کار باعث میشود دانشآموز درک بصری و شهودی از فرآیند تفریق به دست بیاورد. نوشتن هر جزء زیر هم یا تبدیل به کسر نامتعارف، روشهای عددی متفاوتی هستند و نادیده گرفتن بخش کسری، باعث اشتباه در پاسخ خواهد شد.













با سلام ، در حل مثال اوایل مقاله ، در مرحله (7) نتیجه 8 سوم میشود نه 8 پنجم. تشکر
با سلام خدمت شما؛
نکته بیان شده کاملا صحیح است و اصلاحات لازم در روابط اعمال شد.
از همراهی شما با مجله فرارس سپاسگزاریم.
عالی بود به کارمن که خیلی امد توضیحات واضح وروشن این سایت بهترین سایت بود عالی عالی😊😊😊