چگونه در متلب تابع بنویسیم؟ — به زبان ساده

در این نوشتار در مورد تابع نویسی در متلب صحبت می‌کنیم. همان طور که گفتیم متلب یک پلتفرم برنامه نویسی است که به صورت خاص برای مهندسین و دانشمندان ارائه شده است. قلب نرم افزار متلب، امکان برنامه نویسی متلب است و زبان پایه ماتریسی آن این امکان را می‌دهد تا بتوانیم طبیعی ترین پدیده‌های عالم را بر حسب زبان محاسباتی بیان کنیم. در این مقاله به صورت جزئی و دقیق روش تابع نویسی در متلب را معرفی و بررسی می‌کنیم.

انواع تابع نویسی در متلب

به صورت کلی چهار نوع تابع را می‌توان در متلب ساخت که عبارتند از:

• Anonymous Functions
• Local Functions
• Nested Functions
• Private Functions

در ادامه روش ایجاد هر یک از توابع بالا را معرفی و بررسی می‌کنیم.

فیلم آموزش برنامه نویسی متلب MATLAB در فرادرس

کلیک کنید

تابع نویسی در متلب به وسیله Anonymous

یک تابع Anonymous تابعی است که در یک فایل برنامه ذخیره نمی‌شود، اما با متغیری مرتبط است که نوع داده آن «تابع هَندل» (function_handle) است، به این معنا که داده‌ای است که یک تابع را نشان می‌دهد. توابع Anonymous می‌توانند چندین ورودی را پذیرفته و یک خروجی را برگردانند. این توابع می‌توانند فقط یک دستور اجرایی واحد داشته باشند. به عنوان مثال، یک هندل برای یک تابع Anonymous ایجاد کنید که مربع یک عدد را پیدا کند. بدین ترتیب در صفحه دستورات یا commands دستور را به صورت زیر می‌نویسیم:

1>> sqr=@(x) x.^2;

متغیر sqr یک تابع هندل است. علامت @ یک اپراتور برای ایجاد توابع هندل و پرانتزی که بلافاصله پس از @ می‌آید شامل آرگومان‌های ورودی است. این تابع Anonymous یک ورودی x را قبول می‌کند و به طور مشخص یک خروجی را به صورت آرایه‌ای به اندازه x که حاوی مقادیر مربع x است را می‌دهد. برای مثال با تعریف تابع هندلی به صورت بالا مربع عدد 5 را می‌توانید به صورت زیر در صفحه دستورات اجرا کنید و داریم:

1>> a=sqr(5)
2
3a =
4
5    25

ویژگی دیگر توابع هندل این است که می‌توان یک تابع هندل را به عنوان ورودی تابع هندل دیگری تعریف کرد و بر روی آن محاسبات انجام داد. برای مثال می‌خواهیم انتگرال تابع sqr را که در بالا تعریف کردیم در بازه 0 تا 1 به دست آوریم. بدین منظور دستور زیر را در صفحه دستورات می‌نویسیم:

1>> q = integral(sqr,0,1)

بدین ترتیب نتیجه این محاسبه برابر با 0/3333 به دست می‌آید. برای تعریف تابعی با چندین ورودی به صورت زیر عمل می‌کنیم:

1>> myfunction = @(x,y) (x^2 + y^2 + x*y);
2>> x = 1;
3>> y = 10;
4>> z = myfunction(x,y)
5
6z =
7
8   111

اگر بخواهیم چندین تابع هندل یا عملیات جبری را در متلب تعریف کنیم، به این صورت عمل می‌کنیم. فرض کنید می‌خواهیم انتگرال یک تابع چند جمله‌ای را در بازه 0 تا 1 به دست آوریم به این صورت که یکی از ضرایب انتگرال مقدار متغیری دارد. اگر انتگرال مورد نظر به صورت زیر باشد:

$$g(c)=\int_{0}^{1} (x^2+cx+1)dx$$

برای حل این انتگرال به ازای مقادیر متغیر c به صورت زیر عمل می‌کنیم. ابتدا تابع داخل انتگرال را به صورت یک تابع Anonymous می‌نویسیم و داریم:

1>> @(x) (x.^2 + c*x + 1);

سپس عملگر انتگرال را به این تابع اضافه می‌کنیم و سپس یک هندل دیگر با ورودی c را تعریف می‌کنیم. بدین ترتیب با دادن مقدار به c به عنوان ورودی، خروجی به صورت انتگرال تابع مورد نظر با مقدار c مورد نظر محاسبه می‌شود و داریم:

1>> g = @(c) (integral(@(x) (x.^2 + c*x + 1),0,1));

و به عنوان مثال برای مقدار $$c=2$$ داریم:

1>> g(2)
2
3ans =
4
5    2.3333

برای تعریف چند تابع Anonymous به صورت یک آرایه به صورت زیر عمل می‌کنیم و داریم:

1>> f = {@(x) (x.^2);
2     @(y) (y + 10);
3     @(x,y) (x.^2 + y + 10)};

با دادن مقادیر اولیه به x و y هر یک از جملات آرایه را می‌توان به صورت f{n} که n شماره آرایه است، صدا زد و بدین ترتیب به عنوان مثال برای مقادیر x و y که به صورت زیر داده می‌شود، می‌توان خروجی را چاپ کرد و داریم:

1>> x=1;
2>> y=10;
3>> f{1}(x)
4
5ans =
6
7     1
8
9>> f{2}(y)
10
11ans =
12
13    20
14
15>> f{3}(x,y)
16
17ans =
18
19    21

تابع نویسی در متلب توسط Local

در این قسمت اصطلاح تابع محلی یا Local را توضیح داده و نحوه ایجاد و استفاده از توابع محلی را نشان می‌دهیم. فایل‌های برنامه متلب می‌توانند حاوی کد برای بیش از یک تابع باشند. در یک فایل تابع، اولین تابع موجود در فایل را تابع اصلی می‌نامند. این تابع برای توابع موجود در فایل‌های دیگر قابل مشاهده است یا می‌توانید آن را از تابع main فراخوانی کنید. توابع دیگر درون فایل را توابع محلی می‌نامند و بعد از توابع اصلی می‌توانند به هر ترتیب انجام شوند. توابع محلی فقط برای سایر توابع در همان فایل قابل مشاهده هستند. آن‌ها در سایر زبان‌های برنامه نویسی معادل زیر روتین‌ها هستند و گاهی زیر مجموعه توابع نیز نامیده می‌شوند.

از ورژن 2016 متلب می‌توانید توابع محلی را در یک فایل اسکریپت ایجاد کنید، به شرطی که همه آن‌ها بعد از آخرین خط کد اسکریپت ظاهر شوند. برای مثال در ادامه یک فایل تابع به نام mystats.m ایجاد می‌کنیم که شامل یک تابع اصلی mystats و دو تابع محلی mymean و mymedian است. بدین ترتیب داریم:

1function [avg, med] = mystats(x)
2n = length(x);
3avg = mymean(x,n);
4med = mymedian(x,n);
5end
6
7function a = mymean(v,n)
8% MYMEAN Example of a local function.
9
10a = sum(v)/n;
11end
12
13function m = mymedian(v,n)
14% MYMEDIAN Another example of a local function.
15
16w = sort(v);
17if rem(n,2) == 1
18    m = w((n + 1)/2);
19else
20    m = (w(n/2) + w(n/2 + 1))/2;
21end
22end

توابع محلی mymean و mymedian میانگین و میانه لیست ورودی را محاسبه می‌کنند. تابع اصلی mystats طول لیست n را تعیین می‌کند و آن را به توابع محلی منتقل می‌کند.

اگرچه نمی‌توان از طریق صفحه دستورات یا از طریق توابع موجود در فایل‌های دیگر یک تابع محلی را فراخوانی کرد، اما می‌توان با استفاده از تابع help به آن دسترسی پیدا کنید. نام فایل و تابع محلی را مشخص کرده و آنها را با یک کاراکتر > جدا کنید:

1help mystats>mymean

mymean یک مثال از یک تابع محلی است. توابع محلی در فایلی که در آن قرار دارند بر توابع دیگر فایل‌ها برتری دارند. یعنی وقتی یک تابع را در یک فایل برنامه فراخوانی می‌کنید، متلب قبل از جستجوی سایر توابع اصلی، بررسی می‌کند که آیا آن تابع محلی است یا خیر. بنابراین می‌توانید یک نسخه جایگزین از یک تابع خاص ایجاد کنید در حالی که نسخه اصلی را در یک فایل دیگر حفظ می‌کنید.

همه توابع از جمله توابع محلی، دارای فضاهای کاری مخصوص به خود هستند که از فضای کاری اصلی جدا هستند. توابع محلی نمی‌توانند به متغیرهای مورد استفاده در توابع دیگر دسترسی داشته باشند مگر اینکه آن‌ها را به عنوان آرگومان ارسال کنید. در مقابل، توابع تو در تو یا nested (توابع کاملاً درون یک تابع دیگر) می‌توانند به متغیرهای مورد استفاده در توابع حاوی آن‌ها دسترسی داشته باشند.

تابع نویسی در متلب توسط پرایوت یا Private

در این بخش اصطلاح تابع پرایوت یا Private را توضیح می‌دهیم و نحوه ایجاد و استفاده از توابع پرایوت را نشان خواهیم داد. توابع پرایوت زمانی مفید هستند که بخواهید حوزه اثر یک تابع را محدود کنید. شما با ذخیره یک تابع در یک زیر پوشه با نام پریوت، آن را به عنوان تابع پرایوت تعیین می‌کنید. سپس این تابع فقط برای توابع و اسکریپت‌های موجود در فولدری که حاوی زیر پوشه پرایوت است در دسترس خواهد بود.

فیلم آموزش برنامه نویسی متلب برای علوم و مهندسی در فرادرس

کلیک کنید

به عنوان مثال در پوشه‌ای که در مسیر جستجوی متلب قرار دارد، یک پوشه فرعی با نام private ایجاد کنید. پوشه خصوصی را به مسیر اضافه نکنید. در پوشه خصوصی، یک تابع را در فایلی با نام findme.m به صورت زیر ایجاد کنید:

1function findme
2% FINDME  An example of a private function.
3
4disp('You found the private function.')

فولدر متلب را به فولدری که حاوی پوشه پرایوت است تغییر دهید و فایلی با نام visual.m ایجاد کنید.

1function visible
2findme

پوشه فعلی برنامه را به هر مکان دلخواهی تغییر دهید و تابع visible را فراخوانی کنید. خواهید دید که تابع پرایوت را پیدا خواهید کرد. با این حال اگرچه نمی‌توانید تابع پرایوت را از صفحه دستورات یا از توابع خارج از پوشه اصلی که حاوی فایل پرایوت است فراخوانی کنید، اما می‌توانید با دستور help و به صورت زیر به آن دسترسی پیدا کنید:

1help private/findme

findme یک مثال از یک تابع پرایوت است. توابع پرایوت بر توابع استاندارد اولویت دارند، بنابراین متلب یک تابع پرایوت به نام test.m را قبل از یک تابع غیر پرایوت به نام test.m پیدا می‌کند. این موضوع به شما این امکان را می‌دهد که یک نسخه جایگزین از یک تابع خاص را در حالی که نسخه اصلی در پوشه دیگری است حفظ کنید.

تابع نویسی در متلب نوع تو در تو یا Nested

تابع تو در تو یا Nested تابعی است که به طور کامل در یک تابع والد قرار دارد. هر تابعی در یک فایل برنامه می‌تواند شامل یک تابع تو در تو باشد. در مثال زیر، تابعی با نام parent شامل یک تابع تو در تو به نام nestedfx است:

1function parent
2disp('This is the parent function')
3nestedfx
4
5   function nestedfx
6      disp('This is the nested function')
7   end
8
9end

تفاوت اصلی بین توابع تو در تو و سایر انواع توابع این است که آن‌ها می‌توانند به متغیرهایی که در توابع والد خود تعریف شده‌اند دسترسی پیدا کرده و آن‌ها را تغییر دهند. در نتیجه توابع تو در تو می‌توانند از متغیرهایی استفاده کنند که به صراحت به عنوان آرگومان ورودی تعریف نشده‌اند. در تابع والد، می‌توانید هندلی را برای یک تابع تو در تو ایجاد کنید که حاوی داده‌های لازم برای اجرای تابع تو در تو باشد.

تابع نویسی در متلب توسط فایل

اسکریپت و توابع به شما امکان می‌دهند از توالی دستورات با ذخیره آن‌ها در پرونده‌های برنامه استفاده مجدد کنید.

فیلم آموزش برنامه نویسی متلب پیشرفته در فرادرس

کلیک کنید

اسکریپت‌ها ساده ترین نوع برنامه هستند، زیرا دستورات را دقیقاً همانطور که در صفحه دستورات یا commands تایپ می‌کنید ذخیره خواهید کرد. توابع انعطاف پذیری بیشتری را ارائه می‌دهند، در درجه اول به این دلیل که می‌توانید مقادیر ورودی را ارسال کرده و مقادیر خروجی را برگردانید. به عنوان مثال تابع مثال زیر با نام fact فاکتوریل یک عدد (n) را محاسبه می‌کند و نتیجه (f) را برمی‌گرداند.

1function f = fact(n)
2    f = prod(1:n);
3end

این نوع تابع باید در یک فایل تعریف شود، نه در خط فرمان. اغلب، شما یک تابع را در فایل خود ذخیره می‌کنید. در این حالت بهترین روش استفاده از نام یکسان برای تابع و فایل (در این مثال fact.m) است. زیرا متلب برنامه را با نام فایل مرتبط می‌کند. در نتیجه فایل را در فولدر فعلی یا در پوشه‌ای در مسیر جستجوی متلب با نام تابع اصلی ذخیره کنید. حال با فراخوانی تابع در صفحه commands می‌توانید حاصل این تابع را به دست آورید. به این ترتیب داریم:

1x =
2
3     5
4
5>> y=fact(5)

بدین ترتیب نتیجه محاسبه $$5!$$ در صفحه دستورات چاپ می‌شود. از ورژن سال 2016 متلب گزینه دیگری برای ذخیره توابع به وجود آمده و این است که آن‌ها را در انتهای یک فایل اسکریپت قرار دهید. به عنوان مثال، فایلی با نام mystats.m با چند دستور و دو تابع fact و perm ایجاد کنید. این اسکریپت جایگزینی (3،2) را محاسبه می‌کند.

1x = 3;
2y = 2;
3z = perm(x,y)
4
5function p = perm(n,r)
6    p = fact(n)/fact(n-r);
7end
8
9function f = fact(n)
10    f = prod(1:n);
11end

با فراخوانی تابع در صفحه Commands و تایپ کردن mystats می‌توان نتیجه را مشاهده کرد که برابر با 6 است.

تابع نویسی در متلب و رسم توابع در متلب

توابع در متلب در دو .m فایل جداگانه ساخته و فراخوانی می‌شوند. برای ساخت تابع در متلب در یک ادیتور از دستور function استفاده می‌کنیم و خروجی‌ها و ورودی‌های آن تابع را مشخص می‌کنیم.

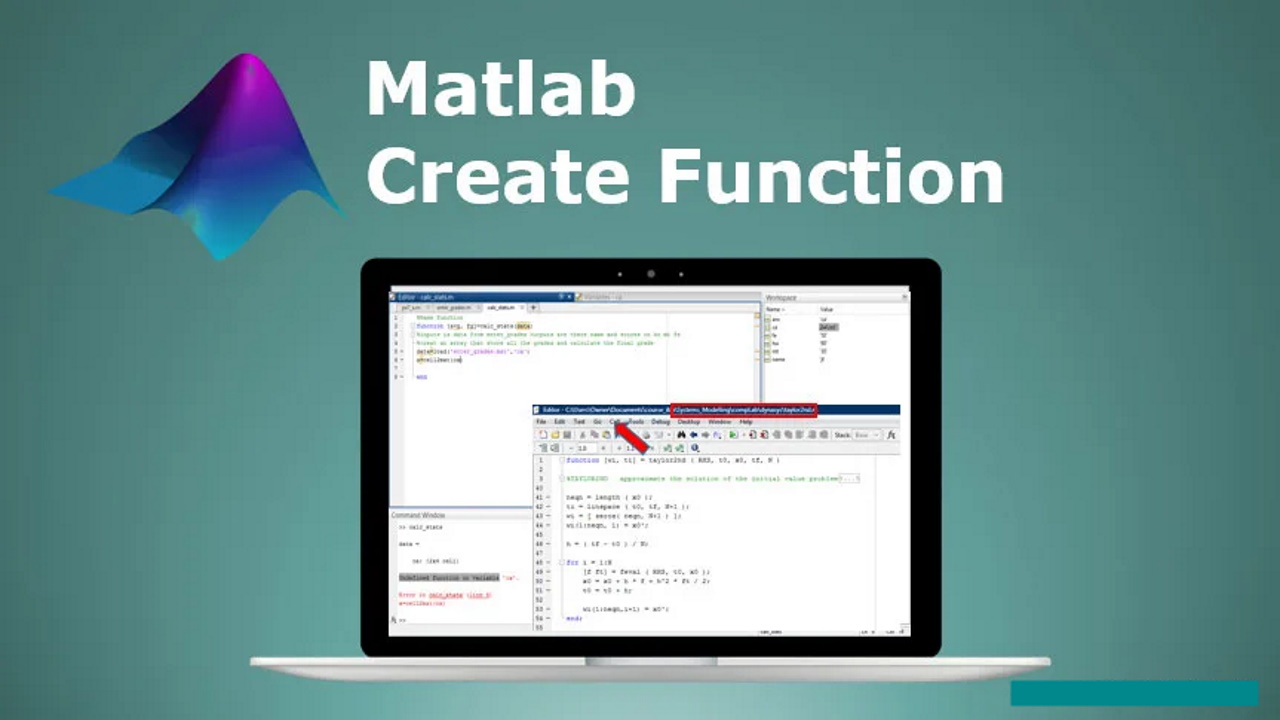
سپس باید این فایل را ذخیره کنیم، مهمترین نکته در این مرحله که باید در نظر گرفت این است که نام تابع شما باید با نام فایل یکسان باشد. یعنی اگر نام تابع شما $$circle$$ است فایل این تابع نیز باید $$circle.m$$ باشد.

فیلم مجموعه آموزش متلب MATLAB – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

برای استفاده از این تابع باید آن را فراخوانی کنیم. بدین منظور در فایل .m دوم فایل را صدا کرده و به ورودی‌ها مقدار می‌دهیم و خروجی‌ها را مشخص می‌کنیم. در این مرحله لزومی ندارد که نام ورودی‌ها و خروجی‌ها با نام ورودی و خروجی تابع یکسان باشد. با اجرا کردن این تابع مقدار خروجی‌ها در صفحه command window متلب نمایش داده می‌شوند.

به عنوان اولین مثال فرض کنید تابعی داریم که می‌خواهد محیط و مساحت دایره را برای ما محاسبه کند. در این حالت خروجی تابع شما محیط و مساحت و ورودی شما شعاع دایره است. بدین منظور به صورت زیر عمل می‌کنیم:

1function [p,s]= circle (r) 
2p=2*pi*r; 
3s=pi*r^2;

نام تابعی که در اینجا انتخاب کرده‌ایم circle است، پس تابع را نیز با همین نام یعنی circle.m ذخیره می‌کنیم. در این حالت خروجی‌های تابع p و s و ورودی‌ تابع r است. در مرحله بعد تابع اصلی را می‌سازیم و در یک ادیتور جدید به صورت زیر عمل می‌کنیم:

1clc; clear; close all 
2radius=4; 
3[p1,s1]= circle(radius)

این صفحه را نیز تحت عنوان main.m ذخیره می‌کنیم. حالا با استفاده از گزینه Run در تابع main مساحت و محیط دایره برای شعاع 4 در command window متلب با اسامی p1 و s1 نمایش داده می‌شوند. دقت کنید که نام توابع ورودی و خروجی تابع main و تابع circle لزوماً نباید یکسان باشد.

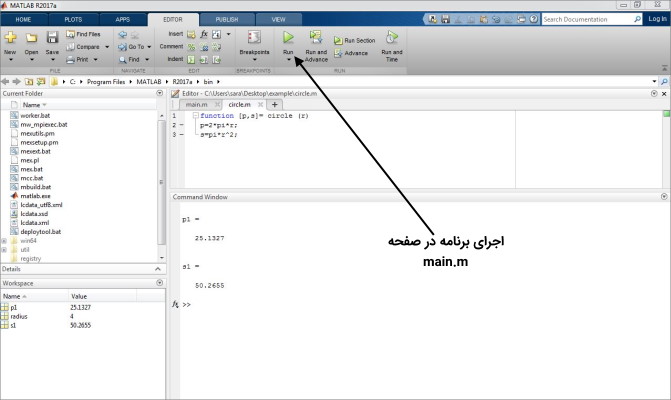
به عنوان مثال دوم می‌خواهیم تابعی بنویسیم که با دریافت مقادیر مختصات مرکز و شعاع یک دایره آن دایره را برای ما رسم کند. همان طور که گفتیم برای تعریف توابع از دو .m فایل استفاده می‌کنیم. در این حالت خروجی تابع گرافیکی است به همین منظور در این حالت از فرمت خروجی= نام تابع (ورودی) استفاده نمی‌کنیم و با نام تابع شروع می‌کنیم و داریم:

1function plot_circle (xc,yc,r) 
2teta=linspace (0,2*pi,100); 
3x=xc+r*cos(teta); 
4y=yc+r*sin(teta); 
5plot(x,y);grid on;

در قسمت بالا مختصات x و y دایره و شعاع را به عنوان ورودی مشخص کردیم. در خط دوم مقادیر زاویه را به صورت 100 نقطه در بازه بین $$0$$ تا $$2\pi$$ مشخص می‌کنیم. حالا مقادیر x و y  هر نقطه روی محیط دایره برابر با تصویر افقی و عمودی شعاع با زاویه مشخص است. در نهایت و در خط آخر دستور plot را برای مقادیر $$x$$ و $$y$$ فراخوانی می‌کنیم. سپس لازم است تابع main را برای این تابع بسازیم و داریم:

1clc; clear; close all
2radius=2;
3x1=3;
4y1=5;
5plot_circle(x1,y1,radius)

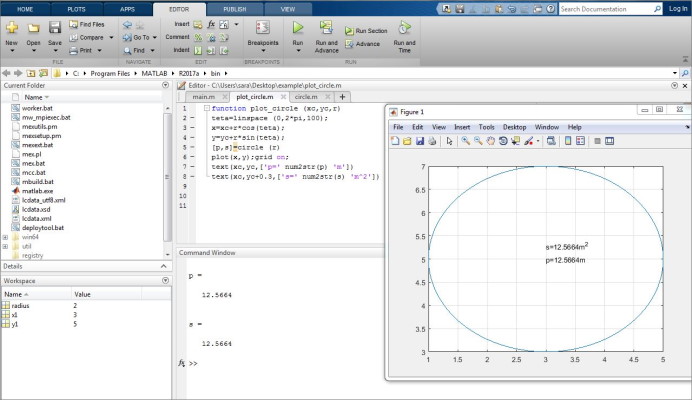
با اجرای تابع main دایره‌ای با مرکز $$(3,5)$$ و با شعاع 2 رسم می‌شود. برای اضافه کردن هر ویژگی به دستور plot آن را در فایل تابع plot_circle.m اضافه می‌کنیم.

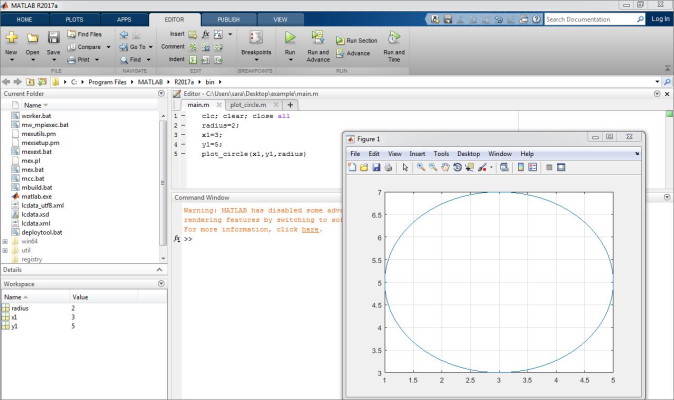
در حالت سوم می‌خواهیم حالتی را بررسی کنیم که از داخل تابع plot_circle تابع circle فراخوانی شود و مقادیر محیط و مساحت در مرکز این دایره چاپ شود، بدین ترتیب تنها تغییر در تابع plot_circle ایجاد می‌شود و داریم:

1function plot_circle (xc,yc,r)
2teta=linspace (0,2*pi,100);
3x=xc+r*cos(teta);
4y=yc+r*sin(teta);
5[p,s]=circle (r)
6plot(x,y);grid on;
7text(xc,yc,['p=' num2str(p) 'm'])
8text(xc,yc+0.3,['s=' num2str(s) 'm^2'])

با اجرای فایل main.m خروجی به صورت زیر خواهد بود:

تابع نویسی در متلب و مشتق تابع در متلب

بهترین راه برای پیدا کردن مشتق یک تابع در متلب استفاده و تعریف یک تابع سمبلیک و سپس استفاده از دستور diff برای محاسبه مشتق تابع است. این موضوع به راحتی در مثال زیر نمایش داده شده است:

1>> syms f(x)
2>> f(x)=x^2-3*x+2
3 
4f(x) =
5 
6x^2 - 3*x + 2
7 
8>> g=diff(f)
9 
10g(x) =
11 
122*x - 3
13 
14>> g(2)
15 
16ans =
17 
181

مقدار مشتق این تابع را می‌توان در یک آرایه از مقادیر x نیز به دست آورد. برای این کار به صورت زیر عمل می‌کنیم:

1>> xValues = [-10 5 88]
2
3xValues =
4
5   -10     5    88
6
7>> g(xValues)
8 
9ans =
10 
11[ -23, 7, 173]

مطالب آموزش متلب در مجله فرادرس

در مجله فرادرس نوشتارهای فراوانی برای آموزش زبان برنامه نویسی متلب وجود دارد که با مطالعه آن‌ها می‌توانید به راحتی به این نرم افزار مسلط شوید و با آن‌ کار کنید. برخی از این مطالب را در ادامه معرفی می‌کنیم:

• نرم افزار متلب چیست و چه کاربردی دارد؟ + معرفی منابع یادگیری Matlab
• برنامه نویسی در متلب (MATLAB) — راهنمای گام به گام (+ دانلود فیلم آموزش رایگان)
• کدهای متلب محاسبات عددی | دانلود رایگان مجموعه کامل
• حل معادله درجه ۲ در متلب | گام به گام (+ دانلود نمونه کد)
• رسم نمودار ماتریس در متلب | گام به گام و کاربردی
• ماتریس در متلب — راهنمای جامع (+ دانلود فیلم آموزش رایگان)
• مشتق در متلب — راهنمای کاربردی
• فاکتوریل در متلب — راهنمای جامع
• رسم تابع در متلب — آموزش گام به گام + نمونه کد
• دستور Sparse در متلب | به زبان ساده
• پخش بار نیوتن رافسون در متلب — از صفر تا صد
• رسم نمودار دو بعدی در متلب (+ دانلود فیلم آموزش رایگان)
• حل دستگاه معادلات دیفرانسیل غیر خطی در متلب | گام به گام

معرفی فیلم‌های آموزش متلب فرادرس

منابع آموزشی نرم افزار متلب بسیار فراوان هستند اما بسیاری از منابع به زبان انگلیسی بوده که این موضوع آموزش را برای کسانی که ممکن است به زبان انگلیسی آشنایی کامل نداشته باشند دشوار می‌کند. همچنین با توجه به اینکه دسترسی به وبسایت متلب به صورت کامل برای کاربران ایرانی فراهم نیست، ممکن است فرآیند آموزش و شبیه سازی با این نرم افزار دشوارتر شود. به این دلیل فرادرس مجموعه دوره‌های آموزش متلب را برای کاربران با کاربردهای مختلف ضبط و آماده کرده است. این آموزش‌ها را به صورت فهرست وار در ادامه معرفی می‌کنیم و برخی از آن‌ها را به صورت جزئی‌تر برای شما توضیح می‌دهیم. مجموعه آموزش متلب فرادرس شامل موارد زیر هستند:

• آموزش برنامه نویسی متلب (MATLAB)
• آموزش برنامه نویسی متلب برای علوم و مهندسی
• مجموعه آموزش های برنامه نویسی متلب پیشرفته
• آموزش طراحی رابط گرافیکی کاربر (GUI) با متلب (MATLAB) – مقدماتی
• آموزش طراحی رابط گرافیکی کاربر (GUI) با متلب (MATLAB) – تکمیلی
• آموزش ساخت ربات تلگرام با متلب (MATLAB)
• آموزش کدهای بلوکی در متلب (MATLAB)
• مجموعه آموزش های واقعیت مجازی و ساخت انیمیشن برای کاربران متلب و سیمولینک
• آموزش رایگان نکات و ترفندهای متلب
• آموزش آشنایی با تولباکس k-Wave در متلب

معرفی فیلم آموزش برنامه نویسی متلب (MATLAB)

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش برنامه نویسی متلب (MATLAB) کرده است. این مجموعه آموزشی از شش درس تشکیل شده و برای دانشجویان رشته‌های مهندسی و علوم پایه مفید است. پیش نیاز این مجموعه آموزش اصول و مبانی برنامه نویسی – (رایگان) است.

درس اول این مجموعه به مقدمات و آشنایی با نرم افزار و زبان برنامه نویسی متلب می‌پردازد و درس دوم انواع داده در متلب را آموزش می‌دهد. درس سوم به ساختارهای کنترل برنامه در متلب و درس چهارم به تعریف و استفاده از توابع در متلب اختصاص دارد. در درس پنجم گرافیک و ترسیم نمودار در متلب را خواهید آموخت و در نهایت در درس ششم و آخر این مجموعه با مدیریت فایل ها و اطلاعات در متلب آشنا خواهید شد.

• برای دیدن فیلم آموزش برنامه نویسی متلب (MATLAB) +‌ اینجا کلیک کنید.

معرفی فیلم آموزش برنامه نویسی متلب برای علوم و مهندسی

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش برنامه نویسی متلب برای علوم و مهندسی کرده است. این مجموعه آموزشی از هشت درس تشکیل شده و برای دانشجویان رشته علوم پایه و فنی مهندسی مفید است. پیش‌نیاز این درس آموزش برنامه نویسی متلب (MATLAB) است.

درس اول این مجموعه به حل معادلات جبری و ریشه‌یابی در متلب اختصاص دارد. درس دوم شامل اعداد تصادفی، محاسبات و تحلیل آماری در متلب است. درس سوم به انتگرال گیری و مشتق گیری عددی در متلب می‌پردازد و درس چهارم به محاسبات نمادین در متلب اختصاص دارد. در درس پنجم در مورد جبرخطی در متلب خواهید آموخت و در درس ششم درون یابی، تقریب تابع و برازش منحنی و سطح در متلب بررسی می‌شود. در نهایت در درس هفتم بهینه سازی کلاسیک در متلب آموزش داده می‌شود و درس هشتم به حل انواع مختلف معادلات دیفرانسیل (Differential Equations) در متلب اختصاص دارد.

• برای دیدن فیلم آموزش برنامه نویسی متلب برای علوم و مهندسی + اینجا کلیک کنید.

معرفی فیلم مجموعه آموزش‌های برنامه نویسی متلب پیشرفته

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم مجموعه آموزش‌های برنامه نویسی متلب پیشرفته کرده است. این مجموعه آموزشی از هفت درس تشکیل شده و برای دانشجویان رشته‌های علوم پایه و مهندسی مفید است. پیش‌نیاز این درس آموزش برنامه نویسی متلب (MATLAB) است.

درس اول این مجموعه به معرفی و آشنایی با ساختارها و آرایه‌های سلولی در متلب می‌پردازد و درس دوم عبارات قانونمند (Regular Expressions) و کاربردهای آن‌ها در متلب را معرفی می‌کند. درس سوم به رویکردهای پیشرفته تعریف و پیاده سازی توابع در متلب اختصاص دارد. در درس چهارم تعریف آرایه‌های توسعه یافته با Container Map را در متلب خواهید آموخت و در درس پنجم این مجموعه ‌مدیریت خطا و حالات استثنائی برنامه‌ها در متلب آموزش داده می‌شود. درس ششم به تایمرها (Timer) و کاربرد آن‌ها در متلب اختصاص دارد و در نهایت در درس هفتم این مجموعه برنامه نویسی شی گرا (Object-Oriented Programming) در متلب آموزش داده می‌شود.

• برای دیدن فیلم مجموعه آموزش‌های برنامه نویسی متلب پیشرفته +‌ اینجا کلیک کنید.

معرفی فیلم مجموعه آموزش های واقعیت مجازی و ساخت انیمیشن برای کاربران متلب و سیمولینک

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم مجموعه آموزش‌های واقعیت مجازی و ساخت انیمیشن برای کاربران متلب و سیمولینک کرده است. این مجموعه آموزشی از هفت درس تشکیل شده و پیش‌نیاز آن آشنایی با برنامه نویسی متلب، فیزیک و ریاضیات دانشگاهی است.

درس اول این مجموعه مقدمه‌ای بر واقعیت مجازی در محیط MATLAB و Simulink است و درس دوم آشنایی با نرم افزار V – Realm Builder را آموزش می‌دهد. درس سوم شامل شبیه سازی انتقال یک مکعب است و درس چهارم به نحوه شبیه سازی نوسان سیستم دو درجه آزادی جرم – فنر – میراگر اختصاص دارد. در درس پنجم و ششم انیمیشن انتقال یک مکعب با استفاده از مدل Simulink و انیمیشن نوسان سیستم جرم – فنر – میراگر با استفاده از مدل سیمولینک آموزش داده می‌شود. در نهایت، در درس هفتم و آخر این مجموعه آشنایی با مدل‌های از پیش آماده شده جعبه ابزار واقعیت مجازی آموزش داده خواهد شد.

• برای دیدن فیلم مجموعه آموزش‌های واقعیت مجازی و ساخت انیمیشن برای کاربران متلب و سیمولینک +‌ اینجا کلیک کنید.

معرفی فیلم آموزش نکات و ترفندهای متلب

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش رایگان نکات و ترفندهای متلب کرده است. این مجموعه آموزشی از بیست قسمت تشکیل شده و برای دانشجویان رشته‌های مهندسی و علوم پایه مفید است. اگر قصد دارید دستورات مهم متلب را در زمان کوتاه فرا بگیرید، این مجموعه آموزشی بسیار مفید است.

درس اول این مجموعه به آشنایی با محیط متلب، توابع clc و clear و متغیر ans و درس دوم توابع سازنده ماتریس‌های مهم مانند zeros ،ones و eye آموزش داده می‌شود. درس سوم ثابت‌ها و علامت‌های مهم و پرکاربرد در متلب را آموزش می‌دهد و درس چهارم شامل تشخیص محدود، نامحدود و نامعین بودن توابع (توابع ifinite ،isinf و isnan) است. درس پنجم و ششم به ترتیب عملگرهای مهم برای تعریف ماتریس‌ها و کلمات کلیدی متلب و تابع iskeyword را پوشش می‌دهد. درس هفتم و هشتم شامل صفحه‌بندی خروجی‌های طولانی با تابع more و قالب‌بندی خروجی با تابع format است. درس نهم و دهم شامل آموزش نمادها و توابع true و false برای مقادیر منطقی و استخراج قطر ماتریس و ساخت ماتریس قطری با تابع diag هستند.

در درس یازدهم ساخت ماتریس‌های قطری بلوکی با تابع blkdiag و در درس دوازدهم کاربردهای عملگر کولون یا دو نقطه و قواعد اندیس‌گذاری آموزش داده می‌شود. کاربرد کلمه end به عنوان اندیس و محاسبه ترانهاده و ترانهاده مزدوج ماتریس‌ها در درس سیزدهم و چهاردهم بررسی می‌شود. در درس پانزدهم و شانزدهم آموزش دستورهای مربوط به آینه‌ای کردن ماتریس‌ها با تابع flip و حالات خاص آن با دو تابع flipud و fliplr و ساخت دنباله حسابی با تابع linspace پوشش داده می‌شود. درس هفدهم به ساخت دنباله هندسی با تابع logspace اختصاص دارد و درس هجدهم کامنت‌گذاری و بلوک‌های کامنت در متلب را آموزش می‌دهد. در نهایت نیز در درس نوزدهم و بیستم فراخوانی فرمان‌های سیستمی در متلب با عملگر ! و الحاق ماتریس‌ها با تابع cat و حالات خاص آن horzcat و vertcat آموزش داده می‌شود.

• برای دیدن فیلم آموزش رایگان نکات و ترفندهای متلب +‌ اینجا کلیک کنید.

جمع‌بندی

در این نوشتار در مورد تابع نویسی در متلب صحبت کردیم. در ابتدا روش‌های تعریف کردن یک تابع را در متلب بیان کردیم و نشان دادیم به چهار روش می‌توان یک تابع را در متلب معرفی کرد. سپس روش تعریف یک تابع را در یک فایل معرفی کردیم، همچنین در مورد رسم یک تابع و مشتق گرفتن از یک تابع نیز مثال‌هایی را مورد توضیح و بررسی قرار دادیم.