بردار و محاسبات آن — به زبان ساده

در مطلب اسکالر و بردار از مجله فرادرس به دو نوع کمیت مختلف اشاره شد که در علم فیزیک از آن‌ها استفاده می‌شود. در این قسمت قصد داریم تا در مورد بردارها صحبت کنیم. بردار، کمیتی است که اندازه و جهت را با هم دارد. این کمیت در تحلیل بسیاری از مفاهیم فیزیکی هم‌چون نیرو، سرعت و شتاب کاربرد دارد.

طول یک بردار، اندازه آن را نشان می‌دهد.

جمع بردارها

به‌منظور جمع زدن دو بردار، انتهای یکی از آن‌ها را به ابتدای دیگری اضافه می‌کنیم.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

در جمع زدن چندین بردار، ترتیب نوشتن آن‌ها اهمیت ندارد و همواره نتیجه یکسانی را می‌دهد. برای نمونه جمع ارائه شده در بالا را می‌توان به شکل زیر نیز بیان کرد.

a+b=b+a

مثال ۱

هواپیمایی به سمت شمال در حال پرواز است. اما از سمت شمال غربی نیز بادی می‌وزد. در این حالت جهت انحراف هواپیما به کدام سمت خواهد بود؟

در این جا با دو بردار اصلی پیشرانش [پیشرانش نیرویی است که هواپیما را رو به جلو حرکت می‌دهد] و باد مواجه هستیم. به‌منظور تعیین جهت پرواز هواپیما، بایستی این دو بردار را با یکدیگر جمع کرد.

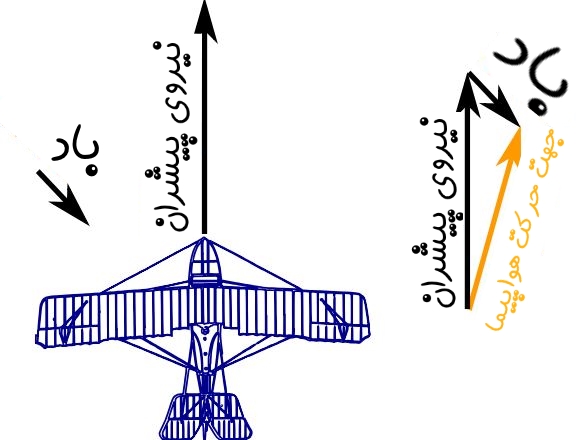
بنابراین اگر شما از زمین، هوایپیما را مشاهده کنید، جهت حرکت آن به شکل زیر است.

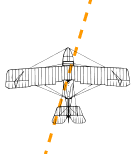
خوب است بدانید که سرعت، شتاب و نیرو از شناخته شده‌ترین کمیت‌های برداری هستند.

تفریق بردارها

دو بردار a و b را تصور کنید. برای رسم بردار a-b، می‌توان این عبارت را به شکل (a+(-b نوشت. بنابراین برای بدست آوردن این عبارت، کافی است که جهت بردار b، معکوس شده و با بردار a جمع شود.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

در شکل زیر بردارهای b ،a و a-b نشان داده شد‌ه‌اند. همان‌طور که ذکر شد، در ابتدا بردار b معکوس شده و سپس a-b بدست آمده است.

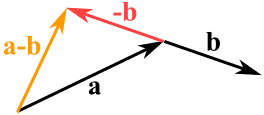
نماد‌های استفاده شده به‌منظور توصیف بردارها

معمولا بردارها را در قالب نماد‌های برجسته‌ای هم‌چون a یا b نشان می‌دهند. هم‌چنین می‌توان آن‌ها به صورت حروف ابتدایی و انتهایشان و مطابق با شکل زیر نشان داد.

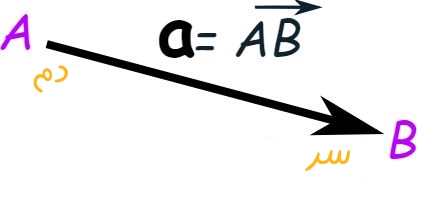
انجام محاسبات

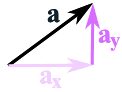
هر بردار را می‌توان به صورت دو یا چند بخش نشان داد. برای مثال بردار a از دو بخش a_x و a_y، مطابق با شکل زیر تشکیل شده است. در ادامه، بیشتر در مورد نحوه تجزیه یک بردار صحبت خواهیم کرد.

جمع بردارها

مطابق با شکل زیر، برای جمع کردن دو بردار، می‌توان بخش‌های x آن‌ها را با یکدیگر و بخش‌های y آن را با هم جمع کرد. برای مثال در دو بردار زیر، مولفه‌های x برابر با 8 و ۲۶ هستند که با یکدیگر جمع شده‌اند. yها نیز به همین شکل، به هم اضافه شده‌اند.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

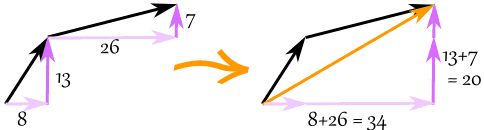
مثال ۲

بردارهای (۱۳ و ۸) = a و (7 و 26) = b را با یکدیگر جمع کنید. همان‌طور که در بالا نیز بیان شد، برای جمع کردن دو بردار، بخش‌های مختلف آن را با هم جمع می‌کنیم. اگر c را برابر با حاصل جمع این دو بردار فرض کنیم، داریم:

c = a + b

c = (8,13) + (26,7) = (8+26,13+7) = (34,20)

تفریق بردارها

همان‌گونه که در بالا نیز اشاره شد، به‌منظور محاسبه تفریق دو بردار می‌توان از معکوس کردن برداری استفاده کرد که بایستی از بردار اول کم شود. برای درک بهتر به مثال ۳ توجه فرمایید.

مثال ۳

دو بردار (k=(4,5 و (v=(12,2 را در نظر بگیرید. با این فرض، عبارت (a=v+(-k را محاسبه کنید. به‌منظور بدست آوردن تفریق مد نظر، در ابتدا بایستی بردار k منفی شده و به v اضافه شود. برمبنای این مفهوم می‌توان گفت:

a = v + −k

a = (12,2) + −(4,5) = (12,2) + (−4,−5) = (12−4,2−5) = (8,−3)

اندازه یک بردار

اندازه یک بردار را با استفاده از دو خط عمودیِ کوچک، در دو طرف بردار، نمایش می‌دهند. . برای نمونه، اندازه بردار a، به شکل زیر نمایش داده می‌شود.

|a|

در بعضی مواقع همانند زیر از دو خط استفاده می‌شود.

||a||

برای محاسبه اندازه یک بردار می‌توان از قانون فیثاغورث، به صورت زیر استفاده کرد.

$$|a|=\sqrt{x^2+y^2}$$

مثال ۴

اندازه بردار (b = (6,8 را محاسبه کنید.

$$|b|=\sqrt{x^2+y^2}=\sqrt{6^2+8^2}=10$$

به برداری با اندازه ۱، بردار واحد گفته می‌شود.

بردار یا اسکالر

کمیتی را که فقط دارای اندازه باشد - و جهتی نداشته باشد، - اسکالر می‌نامند. از طرفی همان‌طور که در بالا نیز بیان شد، یک بردار، اندازه و جهت را توامان دارا است. از طرفی دقت شود که نماد بردار به شکل برجسته است. بنابراین c یک بردار و c یک اسکالر است.

ضرب کردن یک بردار در یک اسکالر

به ضرب کردن هر بردار در یک عدد ثابت - که اسکالر محسوب می‌شود، - «مقیاس گذاری» (Scaling) گفته می‌شود. به‌منظور ضرب کردن یک بردار در یک اسکالر، هر بخش بردار مذکور را بایستی در عددِ اسکار، ضرب کرد.

مثال ۵

بردار (m = (7,3 را در عدد اسکالر ۳ ضرب کنید.

برای این‌کار به شکل زیر عمل خواهد شد.

a = 3m = (3×7,3×3) = (21,9)

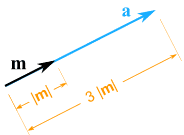
همان‌گونه که در شکل زیر نیز می‌بینید، اندازه بردار m سه برابر شده و جهت آن تغییری نکرده است.

در بخش ضرب بردارها، در مورد ضرب دو بردار در یکدیگر بحث خواهیم کرد.

فراتر از دوبعد

از بردارها می‌توان به منظور توصیف کمیت‌های سه‌بعدی و یا بیشتر نیز استفاده کرد [به‌عنوان مثال به‌منظور توصیف فضا-زمان در نسبیت عام انیشتین، به ۴ بعد نیاز است].

برای نمونه در شکل زیر بردار (1,4,5) در فضای سه‌بعدی نشان داده شده است.

مثال ۶

بردار (a = (3,7,4 و (b = (2,9,11  را با یکدیگر جمع کنید.

c = a + b

(c = (3,7,4) + (2,9,11) = (3+2,7+9,4+11) = (5,16,15

مثال ۷

اندازه بردار (w = (1,−2,3 را بدست آورید.

همانند حالت دو بعدی، در شرایطی که با برداری چند بعدی سر و کار داریم، اندازه را می‌توان با به توان ۲ رساندن هر کدام از مولفه‌های بردار، محاسبه کرد. بنابراین در این حالت (سه بعدی)، اندازه بردار به‌صورت زیر محاسبه می‌شود.

$$|b|=\sqrt{x^2+y^2+z^2}=\sqrt{1^2+(-2)^2+3^2}=\sqrt{1^2+4+9}=\sqrt {14}$$

اندازه و جهت یک بردار

یک بردار را می‌توان به دو شکلِ کارتزینی و یا قطبی توصیف کرد. به‌منظور توصیف بردارها به شکل کارتزینی، از مختصات x و y آن‌ها استفاده می‌شود.

فیلم آموزش ریاضی عمومی ۲ در فرادرس

کلیک کنید

شکل زیر یک بردار را در مختصات کارتزینی نشان می‌دهد.

هم‌چنین به‌منظور توصیف یک بردار در مختصات قطبی، اندازه و زاویه آن نسبت به محور x نشان داده می‌شوند.

شکل زیر یک بردار را به شکل قطبی نشان داده است.

توجه داشته باشید که این دو بیان، معادل هم هستند؛ بنابراین می‌توان آن‌ها را به یکدیگر تبدیل کرد. به‌منظور تبدیل مختصات کارتزینی به قطبی، بایستی از دو فرمول زیر استفاده کرد.

x = r × cos( θ )
y = r × sin( θ )

هم‌چنین اگر بخواهیم یک بردار که به شکل کارتزینی بیان شده را به صورت قطبی بیان کنیم، می‌توانیم از تبدیل زیر استفاده کنیم.

$$r=\sqrt{x^2+y^2}$$
$$θ=tan^{-1} {y \over x}$$

مثال ۸

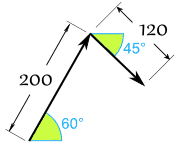
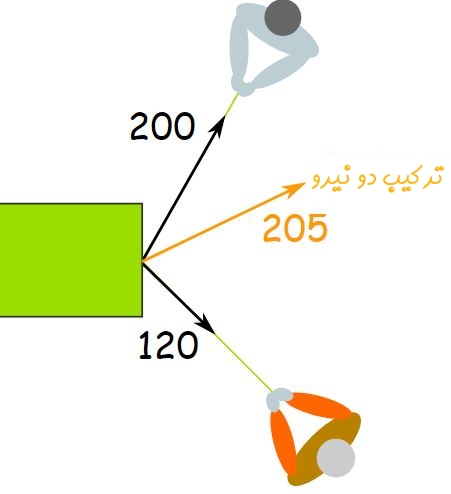
جعفر و علی جعبه‌ای را مطابق شکل زیر به سمت خود می‌کشند. جعفر نیرویی برابر با ۲۰۰ نیوتن، در زاویه ۶۰ درجه و علی نیروی ۱۲۰ نیوتن را در زاویه ۴۵ درجه اعمال می‌کند. جمع برداری این دو نیرو چقدر و در چه جهتی است؟

برای حل این سوال در ابتدا بدون تغییر دادن جهت نیرو‌ها، انتهای یکی از آن‌ها را به ابتدای دیگری وصل می‌کنیم (مطابق شکل زیر).

این بردارها به شکل قطبی بیان شده‌اند، چراکه اندازه و جهت آن‌ها نشان داده شده. به‌منظور جمع برداری این نیرو‌ها، نشان دادن آن‌ها در مختصات کارتزینی، کار را آسان‌تر خواهد کرد. نیروهای وارد شده را می‌توان در دستگاه مختصات کارتزینی و به‌صورت زیر بیان کرد:

بردار نیروی وارد شده توسط جعفر:

x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
y = r × sin( θ ) = 200 × sin(60°) = 200 × 0.8660 = 173.21

بردار نیروی وارد شده توسط علی:

x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0.7071 = 84.85
y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = −84.85

بنابراین شکل تجزیه شده این بردارها به‌ صورت زیر هستند.

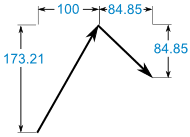
در نتیجه با جمع زدن آن‌ها در مختصات کارتزینی، داریم:

(100, 173.21) + (84.85, −84.85) = (184.85, 88.36)

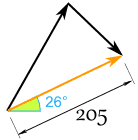
این پاسخ صحیح است، اما در مختصات کارتزینی بیان شده. برای نشان دادن آن‌ها به شکل قطبی، می‌توان از تبدیل ارائه شده در بالا استفاده کرد. بنابراین پاسخ بدست آمده در مختصات قطبی برابر است با:

$$r=\sqrt{x^2+y^2}=\sqrt{184.85^2+88.36^2}=20۵$$
$$θ=tan^{-1} {y \over x}=tan^{-1} {88.36 \over 184.85}=25.5^°$$

از این رو اندازه جمع دو نیرو برابر با ۲۰۵ و زاویه آن ۲۵.۵ درجه است. شماتیک این نیرو در نمودار زیر نشان داده شده.