آمار توصیفی در پایتون با کتابخانه Numpy و Pandas — راهنمای کاربردی

در هر تحقیق و بررسی آماری، بعد از جمع‌آوری داده‌ها، گام بعدی مرحله محاسبه شاخص‌ها و آمار توصیفی است. محاسبه این شاخص‌ها به شناخت رفتار داده‌ها کمک می‌کند و حتی می‌تواند به نظریه پردازی و انجام آزمون فرض منجر شود. این نوشتار به بررسی نحوه اجرای دستورات و کدهای پایتون برای استخراج آمار توصیفی پرداخته است. در این بین برای انجام محاسبات آمار توصیفی در پایتون با کتابخانه Numpy و Pandas کار خواهیم کرد.

برای آشنایی بیشتر با شاخص‌ها و آمارهای توصیفی بهتر است مطلب شاخص های آمار توصیفی در علم داده — راهنمای کاربردی را مطالعه کنید. همچنین به منظور آگاهی از نحوه استفاده از کتابخانه Numpy و Pandas نیز مطالعه پانداس (Pandas) — از صفر تا صد و کتابخانه Numpy در پایتون — راهنمای سریع ضروری به نظر می‌رسد.

آمار توصیفی در پایتون با کتابخانه Numpy و Pandas

کتابخانه Pandas، یک کتابخانه «متن‌باز» (Open Source) به زبان برنامه‌نویسی پایتون است که کارایی بالا در مراحل تحلیل‌های آماری، نظیر «پیش‌پردازش» (PreProcessing) و «تصویرسازی» (Visualization) داده‌ها دارد. از طرفی کتابخانه Numpy یک کتابخانه مهم دیگر در پایتون بخصوص برای تحلیل‌گرهای داده (Data Scientist) است. محاسبات توسط آرایه‌های Numpy درست به مانند لیست‌های پایتون هستند با این تفاوت که از نظر سرعت بسیار سریع‌تر از توابع اصلی پایتون اجرا می‌شوند در نتیجه برای اجرای عملیات ریاضیاتی و منطقی بسیار کارآمدتر هستند. به این ترتیب می‌توان گفت Numpy ابزاری است که استفاده از آن سرعت و کارایی برنامه‌های پایتون را افزایش می‌دهد.

فیلم آموزش کتابخانه های پایتون برای کار با اکسل در فرادرس

کلیک کنید

در این نوشتار با تکیه بر هر دو این کتابخانه‌ها، کدهایی تولید می‌کنیم که محاسبات مربوط به آمار توصیفی (Descriptive Statistics) نظیر معیارها یا شاخص‌های مرکزی، پراکندگی را انجام می‌دهد. ابتدا به ساختار کدهایی در Numpy خواهیم پرداخت که در این امر ما را یاری می‌رسانند و سپس محاسبه چنین شاخص‌هایی را در Pandas مورد بررسی قرار خواهیم داد.

آمار توصیفی در پایتون با کتابخانه Numpy

در ابتدای امر با نحوه محاسبه شاخص‌های مرکزی (Central Tendency)، نظیر میانگین (Mean) و میانه (Median) و همچنین شاخص‌های پراکندگی (Dispersion Measures) مانند واریانس (Variance) و انحراف معیار (Standard Deviation) خواهیم پرداخت. همچنین چندک‌ها (Quartiles) نیز توسط این کتابخانه مورد محاسبه قرار می‌گیرند. به این ترتیب آمار توصیفی در پایتون استخراج شده و نسبت به داده‌ها، اطلاعات بیشتری خواهیم داشت.

فیلم آموزش پانداس pandas برای تحلیل اطلاعات در پایتون در فرادرس

کلیک کنید

برای محاسبات این شاخص‌ها، از یک مجموعه داده به نام رشد دندان‌ها (ToothGroth.csv) استفاده خواهیم کرد که می‌توانید آن را با کلیک روی (+) دریافت کنید. این اطلاعات در قالب یک فایل متنی ثبت شده که ستون‌ها یا متغیرها با علامت «,» (comma) جدا شده‌اند. به همین علت این نوع فایل‌ها را با نام Comma Separated Value یا همان CSV می‌شناسند. متغیرها به صورت $$len$$، $$supp$$ و $$dose$$ هستند. در جدول زیر ۱۵ سطر اول این مجموعه داده مشاهده می‌شود.

کد زیر ابتدا کتابخانه Numpy را فراخوانی کرده و اطلاعات فایل را در متغیر data ذخیره می‌کند.

1import numpy as np
2
3data_file = 'ToothGrowth.csv'
4data = np.genfromtxt(data_file, names=True, delimiter=",", dtype=None)

از آنجایی که اسامی ستون‌ها در سطر اول این فایل نوشته شده‌اند،‌ گزینه name=True‌ انتخاب شده است. همچنین علامت جداکننده مقادیر متغیرها با دستور delimiter نیز همان «,» در نظر گرفته شده است. در کدی که در ادامه مشاهده می‌کنید، برای هر سطح از متغیر supp‌ و dose مقدار آمار توصیفی را برای متغیر کمی len محاسبه می‌کنیم. نتیجه در یک لیست به نام summary_stats قرار گرفته است.

1summary_stats = []
2for supp_lvl in np.unique(data['supp']):
3    
4    for dose_lvl in np.unique(data['dose']):
5    
6        # Subsetting
7        data_to_sum = data[(data['supp'] == supp_lvl) & (data['dose'] == dose_lvl)]
8        # Calculating the descriptives
9        mean = data_to_sum['len'].mean()
10        sd = data_to_sum['len'].std()
11        max_supp = data_to_sum['len'].max()
12        min_supp =  data_to_sum['len'].min()
13        ps = np.percentile(data_to_sum['len'], [25, 75] )
14        summary_stats.append((mean, sd, max_supp, min_supp, ps[0], ps[1], supp_lvl, dose_lvl))

در انتها نیز به کمک دستوراتی که در ادامه مشاهده می‌کنید، لیست را مرتب کرده و نمایش می‌دهیم. واضح است که نتیجه محاسبات آمار توصیفی در پایتون توسط متغیر results ثبت شده است.

1results = np.array(summary_stats, dtype=None)
2np.set_printoptions(suppress=True)
3print(results)

نتیجه اجرای این کد خروجی مانند تصویر زیر خواهد داشت.

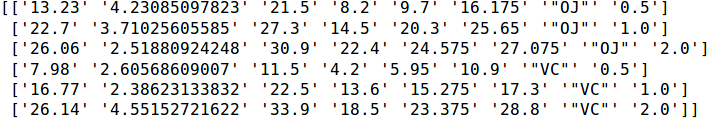
ستون اول مطابق با کدهای نوشته شده مربوط به میانگین (mean) است، همچنین انحراف معیار (std)، مقدار حداکثر (max) و حداقل (min) در ادامه قابل مشاهده‌اند. در انتها نیز چارک اول و سوم (percentile 25 , 75) مشاهده می‌شوند.

نکته: در بیشتر نرم‌افزارهای محاسبات آماری نظیر SPSS و R، منظور از شاخص یا آمارهای توصیفی، میانگین، انحراف معیار، حداکثر، حداقل و چارک‌ها است. در زبان محاسبات آماری R‌ به کمک دستور summary نیز همین شاخص‌ها محاسبه می‌شوند. به نظر می‌رسد که در پایتون نیز همین رویه حفظ شده است.

البته خروجی به شکل زیبا و کاملی نشان داده نشده است. شاید به همین علت است که از کتابخانه Pandas برای محاسبات آماری بیشتر و بهتر استفاده می‌شود. البته نباید محاسبات ساده و سریع را هنگام استفاده از توابع آماری از کتابخانه Numpy‌ فراموش کرد. بنابراین اگر حجم مشاهدات زیاد است بهتر است با Numpy محاسبات را انجام داده و خروجی را با کدهای جداگانه مرتب کرده و نمایش دهیم.

آمار توصیفی در پایتون با کتابخانه Pandas

در این مطلب می‌آموزیم که چگونه آمار توصیفی را با استفاده از کتابخانه Pandas بدست آوریم. در این بین همچنین از بسته‌های دیگر در پایتون مانند NumPy و SciPy نیز استفاده خواهیم کرد. ابتدا با استفاده از توابع موجود در کتابخانه Pandas آمار توصیفی برای مجموعه‌ای از داده‌های شبیه‌سازی شده را محاسبه می‌کنیم.

خوشبختانه کدهای دستوری و همچنین خروجی‌های توابع Pandas بسیار شبیه زبان برنامه‌‌نویسی R است و از ساختار چارچوب داده‌ (DataFrame) شبیه R پشتیبانی می‌کند. در ادامه کدهایی را مشاهده می‌کنید که به منظور فراخوانی کتابخانه‌های مورد نیاز نوشته شده‌اند.

1import numpy as np
2from pandas import DataFrame as df
3from scipy.stats import trim_mean, kurtosis
4from scipy.stats.mstats import mode, gmean, hmean

واضح است که توابع tri_mean و Kutrosis برای محاسبه میانگین پیراسته و کشیدگی استفاده خواهند شد. همچنین توابع mode, gmean و hmean نیز برای بدست آوردن نما، میانگین هندسی و میانگین توافقی یا همساز مورد استفاده قرار می گیرند.

برای تولید داده‌های شبیه‌سازی شده نیز از کد زیر استفاده خواهیم کرد.

1N = 20
2P = ["noise","quiet"]
3Q = [1,2,3]
4
5values = [[998,511], [1119,620], [1300,790]]
6
7mus = np.concatenate([np.repeat(value, N) for value in values])
8
9data = df(data = {'id': [subid for subid in range(N)]*(len(P)*len(Q))
10    ,'iv1': np.concatenate([np.array([p]*N) for p in P]*len(Q))
11    ,'iv2': np.concatenate([np.array([q]*(N*len(P))) for q in Q])
12    ,'rt': np.random.normal(mus, scale=112.0, size=N*len(P)*len(Q))})

این قسمت به منظور تولید داده‌هایی به کار رفته است که از توزیع نرمال بوده و برای دو دسته یا گروه در متغیر iv1 و سه گروه یا دسته در متغیر iv2 تقسیم‌بندی شده‌اند. این داده‌های نرمال، با مراکز یا میانگین (998,511)، (1119,620) و (1300,790) و انحراف استاندارد 112.0 تولید شده‌اند.

فیلم آموزش پانداس pandas برای تحلیل اطلاعات در پایتون در فرادرس

کلیک کنید

برای هر گروه ۲۰ مشاهده تولید می‌شود و از آنجایی که دو تقسیم بندی براساس P و Q ایجاد شده است، تعداد مشاهدات در کل برابر است با:

$$\large Count=N \times \operatorname{len}(Q) \times \operatorname{len}(P) = 20 \times 23\times 2=120$$

این داده‌های در چارچوب داده data ثبت و نگهداری شده‌اند. برای نمایش آمار توصیفی برای این چارچوب داده، با استفاده از کتابخانه Pandas‌ می‌توانید به راحتی با اجرای دستور زیر، یک جدول به عنوان خروجی آمار توصیفی ایجاد کنید.

1data.describe()

نتیجه ظاهر شده، شامل مولفه‌های، تعداد (Count)، میانگین (mean)، انحراف استاندارد (std)، حداقل (min)، چارک اول (25%)، چارک دوم یا میانه (50%) ، چارک سوم (75%) و حداکثر (max) است که درست به مانند حالت قبل، با استانداردهای نرم‌افزارهای محاسبات آماری مطابقت دارد.

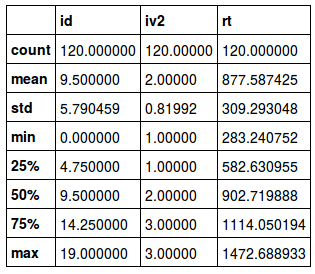
نکته: این شاخص‌ها را می‌توان برای ترسیم نمودار جعبه‌ای (Boxplot) به کار برد، به این ترتیب تقارن و پراکندگی و مرکزیت داده‌ها بوسیله نمایش تصویری مشخص‌تر گزارش می‌شود. برای آشنایی با نحوه ترسیم این نمودار مطلب نمودار جعبه ای (Boxplot) و رسم آن در پایتون – به زبان ساده را بخوانید.

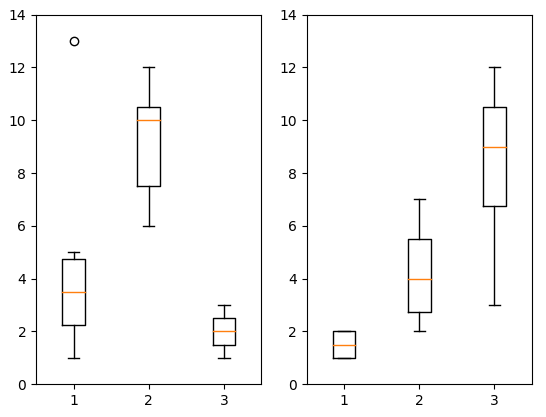
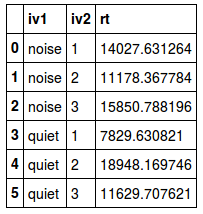
حال سعی می‌کنیم که برای هر سطح از متغیر iv1 و iv2 که توسط مقادیر متغیر Q (شامل ۱ ، ۲ و ۳) مشخص شده و سطوح متغیر P که به صورت noise‌ و quiet تعیین شده، میانگین را محاسبه کنیم. کد زیر که البته بسیار کوتاه است به این منظور نوشته شده است.

1grouped_data = data.groupby(['iv1', 'iv2'])
2grouped_data['rt'].describe().unstack()

خروجی این دستور به صورت یک جدول ظاهر می‌شود که متغیرها در سطرها و برچسب شاخص‌های آماری در ستون‌ها قرار گرفته است.

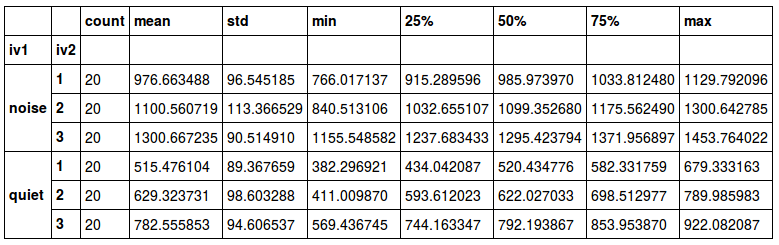
برای مثال به راحتی توسط این جدول می‌توان میانگین متغیر rt را برای مقدار iv2=1 و iv1=noise بدست آورد. این مقدار برابر با 976.6643488 است. خروجی این کد، زیبا و خوانا است و تقسیم‌بندی و طبقه‌بندی سطوح دو متغیر iv1 , iv2 به خوبی در جدول نمایش داده شده است.

فیلم آموزش پانداس pandas برای تحلیل اطلاعات در پایتون در فرادرس

کلیک کنید

محاسبه شاخص‌های تمرکز در Pandas

اگر بخواهید شاخص دلخواه خود را براساس کتابخانه Pandas محاسبه و نمایش دهید، کافی است تابع مورد نظرتان را در کدی به شکل زیر وارد کنید.

1grouped_data['rt'].mean().reset_index()

از آنجایی که تابع ()mean، وظیفه محاسبه میانگین را به عهده دارد، خروجی دستور بالا، محاسبه میانگین برای مجموعه داده grouped_data خواهد بود. واضح است که در این چارچوب اطلاعاتی، مشاهدات برحسب دو متغیر عامل (Factor) به نام‌های iv1 , iv2 تفکیک شده‌اند. همین عمل میانگین‌گیری را می‌توان به کمک روش aggregate در Numpy نیز صورت دارد. کد زیر به این منظور نوشته شده است.

1grouped_data['rt'].aggregate(np.mean).reset_index()

به این ترتیب خروجی به صورت زیر درخواهد آمد. البته استفاده از روش aggregate مزایایی دارد که در ادامه به آن اشاره خواهیم کرد.

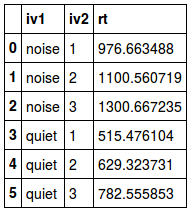
همچنین برای محاسبه شاخص‌های میانگین هندسی (Geometric Mean) و میانگین همساز یا توافقی (Harmonic Mean) باید از تابع apply استفاده کرد. در ادامه کدی را مشاهده می‌کنید که محاسبه میانگین هندسی را امکان‌پذیر کرده است. واضح است که gmean نام تابع محاسبه میانگین هندسی است.

1grouped_data['rt'].apply(gmean, axis=None).reset_index()

همچنین برای محاسبه میانگین همساز نیز از دستور زیر کمک گرفته‌ایم. واضح است که hmean نام تابع محاسبه میانگین همساز است.

1grouped_data['rt'].apply(hmean, axis=None).reset_index()

میانگین پیراسته نیز به کمک روش trimmed mean از کتابخانه SciPy قابل محاسبه است. همانطور که در کد زیر مشاهده می‌کنید با کمک تابع apply و trim_mean محاسبه مربوط به میانگین پیراسته با پارامتر 0.1 صورت گرفته است به این معنی که 10٪ از داده‌ها (۵٪ از بزرگترین و ۵٪ از کوچکترین‌) حذف شده و از مابقی میانگین‌ گرفته شده است. این محاسبات برای هر گروه از ترکیب سطوح متغیرهای طبقه‌ای انجام شده است.

1trimmed_mean = grouped_data['rt'].apply(trim_mean, .1)
2trimmed_mean.reset_index()

نکته: محاسبه میانگین پیراسته و مقایسه آن با میانگین داده‌ها به شناسایی داده‌های پرت و شناخت از چولگی داده‌ها کمک می‌کند. اگر میانگین پیراسته و میانگین حسابی داده‌ها، نزدیک به یکدیگر باشند، شک نسبت به وجود داده‌های پرت یا دورافتاده در بین داده‌ها از بین می‌رود و برعکس اگر اختلاف بین این دو میانگین زیاد باشد، احتمال وجود داده‌های دورافتاده (outlier) زیاد خواهد بود.

خروجی هر یک از این دستورات جدولی است که به صورت متوالی در تصویر زیر دیده می‌شود.

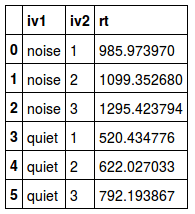
خوشبختانه در Pandas دو روش برای محاسبه میانه (Median) وجود دارد. اولین شیوه می‌تواند استفاده از روش aggregate یا بدون آن باشد. در خط اول کد زیر به تنهایی از تابع median‌ استفاده شده و در خط بعدی به کمک aggregate‌ این کار صورت گرفته است.

1grouped_data['rt'].median().reset_index()
2grouped_data['rt'].aggregate(np.median).reset_index()

نتیجه به مانند تصویر زیر خواهد بود. البته به یاد دارید که میانه همان چارک دوم داده‌ها است. بد نیست که خروجی این دستورات که در جدول ۵ بدست آمده را با خروجی مربوط به آمار توصیفی در پایتون و محاسبه صورت گرفته در ستون (۵۰٪) در جدول ۲ مقایسه کنید.

فیلم آموزش پانداس pandas برای تحلیل اطلاعات در پایتون در فرادرس

کلیک کنید

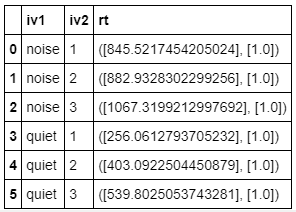
از طرفی برای محاسبه نما (mode) نیز از کتابخانه SciPy‌ استفاده خواهیم کرد.

1grouped_data['rt'].apply(mode, axis=None).reset_index()

نکته: برای محاسبه نما، کتابخانه Pandas نیز دارای تابع است ولی متاسفانه برای داده‌های طبقه‌بندی شده کاربرد ندارد.

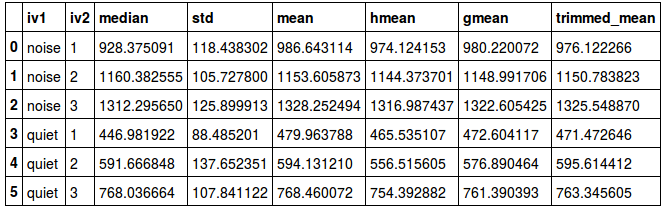
اگر می‌خواهید همه محاسبات مربوط به شاخص‌های تمرکز (Central Tendency) را در یک جدول مشاهده کنید، از کد زیر کمک بگیرید.

1descr = grouped_data['rt'].aggregate([np.median, np.std, np.mean]).reset_index()
2descr['trimmed_mean'] = pd.Series(trimmed_mean.values, index=descr.index)
3descr

با اجرای کد بالا، در یک ساختار جدولی به مانند تصویر زیر، شاخص‌های تمرکز برای هر سطح از متغیرهای طبقه‌ای iv1 و iv2، محاسبه و نمایش داده می‌شوند.

استفاده از معیار تمرکز برای مقایسه دو یا چند مجموعه داده ممکن است خطرناک باشد زیرا جنبه‌های دیگر رفتار داده‌ها نظیر پراکندگی، در نظر گرفته نشده‌اند. در گام بعدی به نحوه محاسبه شاخص‌های پراکندگی خواهیم پرداخت که برای شناخت رفتار و توزیع داده‌ها مهم هستند.

فیلم آموزش پانداس pandas برای تحلیل اطلاعات در پایتون در فرادرس

کلیک کنید

شاخص‌های پراکندگی در Pandas

همانطور که در قسمت قبلی اشاره شد به منظور شناخت از داده‌ها، شاخص‌های تمرکز محاسبه می‌شوند. ولی باید از طرفی نشان دهیم که این داده‌ها نسبت به نقطه تمرکز چقدر دور یا نزدیک هستند. به این ترتیب متوجه می‌شویم که آیا شاخص تمرکز، معیار خوبی برای نمایندگی همه داده خواهد بود یا خیر. در این قسمت به نحوه محاسبه شاخص‌های پراکندگی خواهیم پرداخت تا اطلاعات بیشتری از داده‌ها جمع‌آوری شده داشته باشیم و نسبت به آن‌ها آگاهی بیشتری کسب کنیم. مجموعه شاخص‌های تمرکز و پراکندگی، آمار توصیفی در پایتون را می‌سازند.

شاخص‌های پراکندگی، معمولا عدم تمرکز داده‌ها را می‌سنجند. از شاخص‌های مهم در این زمینه می‌توان به انحراف استاندارد (Standard Deviation)، واریانس (Variance) و دامنه میان چارکی (Inter Quartile Range) اشاره کرد. هر یک از این شاخص‌ها به شکلی پراکندگی را اندازه‌گیری می‌کنند. برای مثال در محاسبه انحراف استاندارد و واریانس میزان پراکندگی حول میانگین سنجیده می‌شود در حالیکه در دامنه (Range) و دامنه میان چارکی،  نقطه مرکزی در نظر گرفته نشده و حداکثر میزان پراکندگی بین داده‌ها محاسبه می‌شود.

برای محاسبه انحراف استاندارد برای گروه‌های مجموعه داده grouped_data کافی است، کد زیر را اجرا کنید.

1grouped_data['rt'].std().reset_index()

برای بدست آوردن واریانس نیز کافی است که از تابع ()var‌ به جای ()std‌ استفاده کنید. به این ترتیب با استفاده از کتابخانه Pandas به راحتی می‌توانید واریانس را محاسبه کنید. کد زیر به این منظور تهیه شده است.

1grouped_data['rt'].var().reset_index()

جدول ۷ نتیجه اجرای این دستور است. مشخص است که برای هر سطح از متغیرهای طبقه‌ای iv1 و iv2 مقدار واریانس برای متغیر rt محاسبه شده است. اگر از هر یک از این مقادیر جذر یا ریشه دوم بگیرید،‌ باز هم انحراف استاندارد حاصل خواهد شد.

نکته: به یاد دارید که داده‌های تولید شده در این مثال از توزیع نرمال با انحراف معیار 112.0 نمونه‌گیری شده بودند. در نتیجه واریانس باید حدود 12544 باشد. در بیشتر گروه‌ها نیز واریانس نمونه‌ها به واریانس توزیع جامعه آماری که نمونه‌ها از آن استخراج شده‌اند نزدیک است.

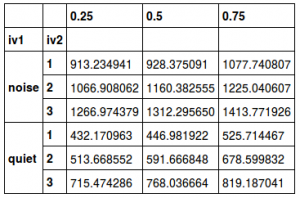
می‌دانیم که دامنه میان چارکی، از تفاضل چارک اول و سوم بدست می‌آید. به این منظور ابتدا چارک‌ها را توسط کد زیر محاسبه کرده، سپس می‌توان ستون (0.25) را از (0.75) کم کنیم. توسط کد زیر چارک‌ها را محاسبه کرده‌ایم. پارامتر ()unstack باعث خوانایی بیشتر این جدول خواهد شد.

1grouped_data['rt'].quantile([.25, .5, .75]).unstack()

خروجی این دستور مطابق با تصویر زیر است.

ذخیره‌سازی خروجی‌ها در قالب اکسل

اگر لازم است آمار توصیفی در پایتون را در قالب اکسل یا فایل‌های متنی csv ذخیره کنید، بهتر است از دستور تبدیل خروجی‌های چارچوب داده (Dataframe) در Pandas‌ به فایل‌های csv کمک بگیریم. در ادامه کد دستوری برای انجام چنین کاری نوشته شده است.

1descr.to_csv('Descriptive_Statistics_in_Python.csv', index=False)

در تصویر زیر نمونه فایل ثبت شده اکسل قابل مشاهده است.

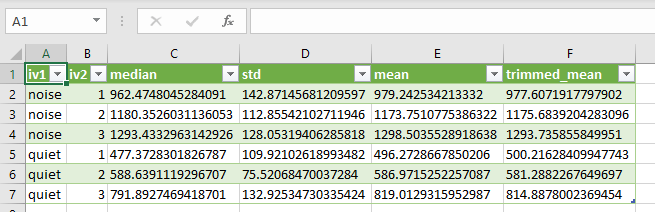
در این خروجی، شاخص‌های آمار توصیفی در پایتون که در جدول 7 ایجاد شده بودند در قالب فایل متنی به نام Descriptive_Statistics_in_Python.csv ذخیره شده است. به یاد دارید که برای نمایش فایل‌های متنی که ستون‌های آن با علامت کاما جدا شده‌اند، می‌توان از اکسل کمک گرفت. به همین دلیل تصویری که مشاهده می‌شود، یک فایل اکسل را نمایش می‌دهد.

فیلم آموزش پانداس pandas برای تحلیل اطلاعات در پایتون در فرادرس

کلیک کنید

خلاصه و جمع‌بندی

اکنون می‌توانید با استفاده کتابخانه‌های Pandas ،NumPy و SciPy محاسبات آمار توصیفی در پایتون را انجام دهید. شیوه کد نویسی و کدهای نوشته شده واقعاً ساده بوده و مراحل انجا کار به آسانی صورت گرفت. یکی از مزیت‌های مهم این روش‌ها و جمع‌بندی این است که می‌توان آن‌ها را توسعه داده و به شاخص‌های آمار توصیفی، گزینه‌ها یا محاسبات دیگری را هم اضافه کرد. به منظور دسترسی به کدهای نوشته شده برای استخراج آمار توصیفی در پایتون که در این متن به آن اشاره شد، می‌توانید به دفترچه ژوپیتر (+) مراجعه کنید.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های برنامه نویسی پایتون
• آموزش تکمیلی برنامه نویسی پایتون
• مجموعه آموزش های آمار، احتمالات و داده‌کاوی
• آموزش کار با پیش پردازش ها در یادگیری ماشین با پایتون (Python)
• کتابخانه NumPy پایتون – راهنمای جامع — بخش اول
• تقلب‌نامه (Cheat Sheet) پایتون برای علم داده (کتابخانه NumPy)
• برنامه نویسی پایتون (Python) با کتابخانه NumPy — به زبان ساده

^^