قضیه کار و انرژی — آموزش سریع و ساده

واژه کار در زندگی روزمره ما به وفور مورد استفاده قرار می‌گیرد و منظور از به کار بردن این واژه، انجام یک عمل است. برای مثال، این کار می‌تواند مطالعه مطلب پیش رو در وبلاگ فرادرس باشد. اما این عمل در فیزیک، تعریف درستی از کار نمی‌باشد. قضیه کار و انرژی به بررسی دقیق مفهوم فیزیکی کار می‌پردازد. در واقع، کار در فیزیک شامل فعالیت‌هایی است که در آن‌ها اعمال نیرو باعث ایجاد جابه‌جایی می‌شود. قضیه کار و انرژی، رابطه‌ای است که ارتباط بین کار انجام شده و تغییرات انرژی جنبشی جسم را مورد بررسی قرار می‌دهد و بیان می‌کند که کار انجام شده روی جسم برابر با تغییر انرژی جنبشی آن جسم است. این مفهوم کاربرد بسیار زیادی در علم فیزیک و مکانیک دارد و از آن برای درک بهتر مسائل آیرودینامیک و دینامیک استفاده می‌شود.

این مطلب ابتدا به صورت دقیق به بررسی مفهوم کار می‌پردازد و در ادامه رابطه کلی قضیه کار و انرژی و مفهوم آن مورد بررسی قرار می‌گیرد. سپس اثبات قضیه کار و انرژی در دو حالت نیرو ثابت و متغیر، انجام می‌شود و در نهایت با استفاده از چند مثال، شیوه استفاده از این قضیه در مسائل گوناگون مورد بررسی قرار می‌گیرد.

قضیه کار و انرژی

همانطور که بیان شد، کار مفهومی در فیزیک است که طی آن، اعمال نیرو باعث جابه‌جایی یک ذره می‌شود. طبق تعریف ارائه شده، در صورتی که جابه‌جایی وجود نداشته باشد، کار نیز برابر با صفر خواهد بود. برای مثال در صورتی که شما برای مدت طولانی در یک مکان ایستاده باشید، بسیار خسته خواهید شد و انرژی بسیار زیادی را مصرف خواهید کرد ولی طبق تعریف فیزیکی کار، شما کاری انجام نداده‌اید.

بنابراین همانطور که اشاره شد، کار نتیجه اعمال نیرو و جابه‌جایی حاصل از آن است. در ادامه باید توجه کرد که تمام اجسام متحرک، دارای انرژی جنبشی هستند. بنابراین باید ارتباطی بین کار و انرژی جنبشی موجود باشد. این ارتباط با استفاده از قضیه کار و انرژی بیان می‌شود و رابطه آن به شکل زیر است.

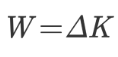
در این رابطه W، کار انجام شده در واحد ژول (J) را نشان می‌دهد و $$\Delta K$$ تغییر انرژی جنبشی جسم را بیان می‌کند. نکته مهم دیگری که باید به آن اشاره کرد، این است که کار به عنوان یک کمیت اسکالر در نظر گرفته می‌شود. همچنین درک مطالب پیش رو، نیاز به درک صحیح و تسط بر شیوه جمع دو یا چند بردار با یکدیگر دارد. در ادامه شیوه اثبات قضیه کار و انرژی در دو حالت مختلف بیان شده است.

اثبات قضیه کار و انرژی

قضیه کار و انرژی با استفاده از دو دیدگاه مختلف مورد بررسی قرار می‌گیرد. حالت اول دیدگاهی است که در آن، کار انجام شده با استفاده از نیروی ثابت، ایجاد شده است و در حالت دوم نیروی متغیر عامل ایجاد کار در مجموعه است.

کار انجام شده با استفاده از نیروی ثابت

طبق قانون دوم نیوتن، زمانی که نیرو ثابت باشد، شتاب نیز ثابت است. بنابراین همانطور که می‌دانیم، معادله حرکت برای جسمی که شتاب ثابت دارد و مقدار جابه‌جایی آن معلوم است به شکل زیر بیان می‌شود. این رابطه را معادله مستقل از زمان نیز می‌نامند.

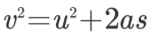
در این رابطه، v سرعت نهایی جسم و u سرعت اولیه آن را نمایش می‌دهد. a شتاب ثابت حرکت جسم است و s مقدار جابه‌جایی در شرایط ذکر شده را بیان می‌کند. این رابطه را می‌توان به فرم رایج زیر هم نمایش داد.

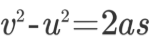
در ادامه، مقادیر رابطه بالا را با مقادیر برداری آن‌ها جایگزین می‌کنیم. با استفاده از این اقدام، رابطه فوق در نهایت به فرم رابطه زیر در می‌آید.

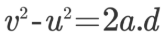
سمت راست این معادله، نشان‌ دهنده ضرب داخلی دو بردار شتاب و جابه‌جایی است. در صورتی که طرفین رابطه بالا را در عبارت m/2 ضرب کنیم، این رابطه به شکل زیر بازنویسی می‌شود.

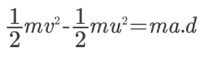
رابطه بالا را می‌توان به کمک قانون دوم نیوتن ساده‌تر کرد. قانون دوم نیوتن بیان می‌کند که حاصل ضرب جرم در شتاب آن جسم (ma)، نیروی وارد بر آن جسم را نشان می‌دهد. بنابراین رابطه بالا به شکل زیر قابل بازنویسی است.

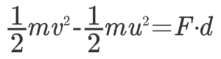
نکته دیگری که باید به آن اشاره کرد این است که عبارت $${1 \over 2} m v^2$$ انرژی جنبشی را نشان می‌دهد و عبارت $$F . d$$ بیانگر کار انجام شده است. بر این اساس، رابطه بالا به فرم زیر بازنویسی می‌شود.

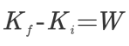
زیروندهای f و i در رابطه بالا، به ترتیب حالت نهایی و ابتدایی را بیان می‌کنند. معادله بالا در نهایت به شکل زیر در می‌آید.

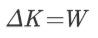
رابطه فوق، قضیه کار و انرژی را نشان می‌دهد و بیان می‌کند که کار انجام شده روی جسم برابر با تغییر انرژی جنبشی آن جسم است. روند فوق برای حالتی بیان شد که نیروی ثابت، عامل ایجاد کار باشد. در حالتی که نیروی متغیر به سیستم اعمال شود، اثبات قضیه کار و انرژی متفاوت خواهد بود که روند آن، در بخش بعدی بیان می‌شود.

کار انجام شده با استفاده از نیروی متغیر

بخش قبل به بررسی حالتی پرداخت که در آن، نیروی ثابت به جسم وارد می‌شد. اما در دنیای واقعی، اعمال نیروی ثابت به ندرت مشاهده می‌شود و حضور نیروی متغیر، مسئله‌ای است که به صورت رایج در زندگی روزمره، شاهد آن هستیم. بنابراین در این قسمت اثبات قضیه کار و انرژی برای حالتی مورد بررسی قرار می‌گیرد که در آن، نیروی متغیر به سیستم اعمال می‌شود.

اثبات قضیه کار و انرژی برای حالتی که نیرو متغیر است، اندکی پیچیده به نظر می‌رسد و نیاز به استفاده از روش‌ها و حقه‌های خاصی است. برای شروع اثبات، ابتدا نموداری را در نظر بگیرید که یک محور آن، نیرو وارد شده بر جسم را نشان می‌دهد و نمودار دیگر میزان جابه‌جایی را بیان می‌کند.

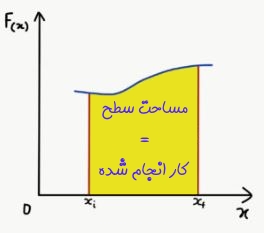
محور x نمودار بالا، میزان جابه‌جایی را نشان می‌دهد. در ادامه، سطح زیر نمودار نشان داده شده در شکل بالا را به مستطیل‌هایی در طول محور x (مطابق شکل زیر) با مساحت بینهایت کوچک تقسیم می‌کنیم.

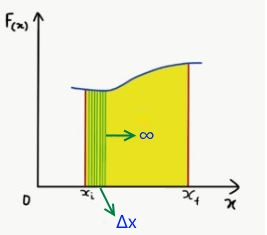
در این قسمت، نیرو را در طول یک جابه‌جایی بسیار کوچک ($$\Delta x$$)، ثابت فرض می‌کنیم. این مورد با توجه به نموداری که در شکل بالا نمایش داده شده، فرض درستی است. بنابراین رابطه کار انجام شده در این جابه‌جایی به شکل زیر نشان داده می‌شود.

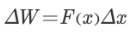
در صورتی که تمام مستطیل‌ها، در نمودار شکل بالا را با یکدیگر جمع کنیم، کار کل به شکل زیر محاسبه می‌شود.

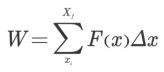
فرض کنید که تعداد مستطیل‌ها در روابط بالا، بینهایت باشد، در این حالت، عرض مستطیل‌ها ($$\Delta x$$) به سمت صفر میل‌  می‌کند و کار کل با استفاده از رابطه حدی زیر قابل محاسبه است.

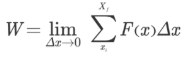
این رابطه را برای سیستم نشان داده شده می‌توان به صورت انتگرال معین نیرو در جابه‌جایی کل، مطابق با رابطه زیر بیان کرد.

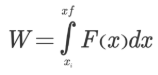
حال به بررسی انرژی جنبشی می‌پردازیم. رابطه این انرژی به صورت زیر قابل بیان است.

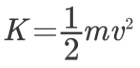
مشتق انرژی جنبشی نسبت به زمان را می‌توان به شکل زیر نمایش داد.

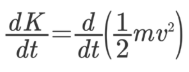
با توجه به آنکه، جرم جسم با زمان تغییر نمی‌کند، می‌توان مقدار آن را از داخل پرانتز خارج کرد و مشتق عبارت باقی مانده را برحسب مشتق سرعت بیان کرد. بر این اساس، رابطه فوق به شکل زیر بازنویسی می‌شود.

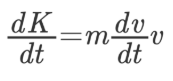
برای ساده‌سازی رابطه بالا توجه کنید که مشتق زمانی سرعت، برابر با شتاب خواهد بود. بنابراین می‌توان رابطه بالا را بر حسب شتاب به شکل زیر نوشت:

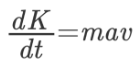
با دقت به رابطه بالا متوجه می‌شویم که می‌توان حاصل ضرب جرم و شتاب را با نیرو جایگزین کرد. در واقع با استفاده از قانون دوم نیوتن (F=ma)، رابطه بالا به شکل زیر ساده‌سازی می‌شود.

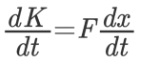
همانطور که مشاهده می‌شود، مشتق زمانی در هر دو طرف رابطه بالا حضور دارد و برای ساده‌تر شدن رابطه، می‌توان این مشتق زمانی را از دو طرف رابطه بالا حذف کرد. بنابراین این رابطه به شکل زیر بازنویسی می‌شود.

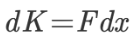
در ادامه برای محاسبه تغییرات انرژی جنبشی در کل جابه‌جایی انجام شده، از طرفین عبارت فوق انتگرال می‌گیریم. بنابراین داریم:

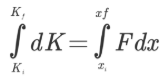
سمت چپ رابطه فوق نشان‌ دهنده تغییرات انرژی جنبشی از ابتدا تا انتهای حرکت است و می‌توان آن را به شکل زیر هم نمایش داد.

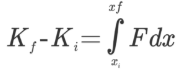
تغییر انرژی جنبشی با علامت Δ نیز قابل بیان است. بنابراین داریم:

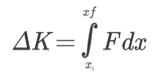
در قسمت بالاتر نشان دادیم که سمت راست رابطه بالا، کار انجام شده را نمایش می‌دهد. بنابراین در نهایت، رابطه بالا به شکل زیر در می‌آید.

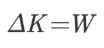
بر این اساس با استفاده از مراحلی که در بالا طی شد، قضیه کار و انرژی برای نیروی متغیر نیز به اثبات رسید. در رابطه بالا، W کار خالصی اعمال شده روی جسم را نشان می‌دهد و $$\Delta K$$ بیان‌ کننده تغییر انرژی جنبشی جسم است.

مثال‌ها

در این بخش، به بیان چند مثال برای آشنایی با شیوه کاربرد رابطه کار و انرژی پرداخته می‌شود. شیوه محاسبه کار نیروها و در نظر گرفتن شرایط اولیه و نهایی مناسب، از نکات قابل توجه در قضیه کار و انرژی است که تنها با استفاده از مثال‌های متنوع، قابل درک است. پیشنهاد ما این است که قبل از خواندن پاسخ مسائل، یک بار خودتان آن‌ها را حل کنید و در نهایت پاسخ خود را با راه حل ارائه شده در این مطلب مقایسه کنید. این روش کمک بسیار زیادی به پیشرفت شما در پاسخ به مسائل گوناگون می‌کند.

مثال 1

آجری به جرم 1 کیلوگرم را در نظر بگیرید. این آجر از ارتفاع 10 متری پرتاب می‌شود. کار انجام شده روی آجر را بین لحظه رها شدن و لحظه رسیدن به زمین محاسبه کنید.

در گام اول، اطلاعات مهمی که در صورت سوال داده شده را بازنویسی می‌کنیم. جرم جسم برابر با 1 کیلوگرم فرض شده و ارتفاع اولیه و انتهایی جسم نیز به ترتیب برابر با 10 و 0 متر در نظر گرفته شده است. خواسته مسئله نیز محاسبه کار انجام شده روی جسم است.

در این مثال، انرژی جنبشی با نماد E_k و انرژی پتانسیل با نماد E_p نشان داده می‌شود. انرژی پتانسیل جسم در ارتفاع ۱۰ متری مطابق با رابطه زیر است.

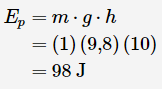
زمانی که آجر در ارتفاع ۱0 متری و در حالت سکون قرار دارد، انرژی پتانسیل آن برابر با 98 ژول و انرژی جنبشی آن صفر است. زمانی که آجر به ارتفاع صفر می‌رسد، تمام انرژی پتانسیل آن به انرژی جنبشی تبدیل می‌شود. بنابراین انرژی جنبشی آجر در انتهای مسیر برابر با 98 ژول خواهد بود.

طبق قضیه کار و انرژی، کار انجام شده روی آجر، برابر با تغییر انرژی جنبشی در مسیر است و به شکل زیر محاسبه می‌شود.

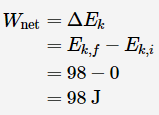
بنابراین کار انجام شده روی آجر که خواسته مسئله بود، برابر با 98 ژول محاسبه شده است.

مثال ۲

اتومبیلی به جرم 1000 کیلوگرم، با سرعت 16.7m/s در حال حرکت است. راننده با دیدن چراغ قرمز، ترمز می‌کند. ترمز اتومبیل نیروی اصطکاک برابر با 8000 نیوتن به اتومبیل وارد می‌کند. در شرایط ذکر شده، مسافتی که طول می‌کشد تا اتومبیل متوقف شود را محاسبه کنید.

ابتدا ورودی‌ها و خروجی مسئله را مشخص می‌کنیم. در این مثال، جرم جسم برابر با 1000 کیلوگرم، سرعت اولیه آن 16.7 متر بر ثانیه و نیروی اصطکاک ترمزها برابر با 8000 نیوتن در نظر گرفته شده است. توجه شود که نیروی اصطکاک در خلاف جهت حرکت اتومبیل به آن وارد می‌شود. طول مسیر توقف اتومبیل نیز خروجی مطلوب مسئله است.

برای به دست آوردن پاسخ این مسئله، قضیه کار و انرژی را در آن به کار می‌بریم. همانطور که می‌دانیم در طول مسیر ترمز، تمام انرژی جنبشی اتومبیل از بین می‌رود. بنابراین تغییرات انرژی جنبشی اتومبیل با کار ناشی از نیروی اصطکاک ترمزهای اتومبیل برابر است.

بنابراین ابتدا انرژی جنبشی اتومبیل را در لحظه‌ ترمز گرفتن، محاسبه می‌کنیم. رابطه این انرژی جنبشی با استفاده از رابطه زیر قابل بیان است.

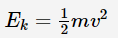
همانطور که بیان شد، این انرژی (رابطه بالا) با کار انجام شده توسط ترمزها برابر است. از آنجایی که نیروی اعمال شده توسط ترمزها معلوم است، کار ترمز با استفاده از رابطه زیر محاسبه می‌شود.

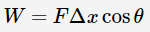
در این رابطه F، نیروی اعمال شده توسط ترمزها، $$\Delta x$$ میزان جابه‌جایی اتومبیل حین فرایند ترمز گرفتن و θ زاویه بین بردار نیروی ترمز و جابه‌جایی اتومبیل را نشان می‌دهند.

انرژی جنبشی اتومبیل با استفاده از مقادیر داده شده به شکل زیر قابل محاسبه است.

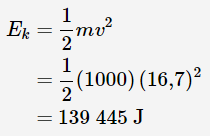
برای محاسبه کار ترمز با استفاده از رابطه داده شده، نیاز به معرفی زاویه θ داریم. همانطور که می‌دانیم، بردار نیروی ترمز و جابه‌جایی در این مثال در خلاف جهت یکدیگر هستند. بنابراین زاویه بین این دو بردار برابر با 180 درجه است. بر این اساس، کار ترمز به شکل زیر محاسبه می‌شود.

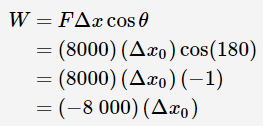
طبق قضیه کار و انرژی می‌دانیم که تغییر در انرژی جنبشی با کار انجام شده برابر هستند. بنابراین داریم:

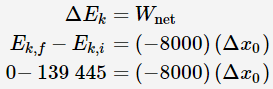
در نهایت جابه‌جایی اتومبیل حین فرایند ترمز، به شکل زیر محاسبه می‌شود.

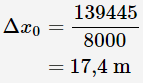
همانطور که بیان شد، کار به فعالیتی گفته می‌شود که طی آن، اعمال نیرو باعث جابه‌جایی یک ذره شود. در واقع کار، نتیجه اعمال نیرو و جابه‌جایی حاصل از آن است. قضیه کار و انرژی، رابطه‌ای است که ارتباط بین کار انجام شده و تغییرات انرژی جنبشی را مورد بررسی قرار می‌دهد و بیان می‌کند که کار انجام شده روی جسم برابر با تغییر انرژی جنبشی آن جسم است.

این مطلب ابتدا مفهوم کار را به صورت دقیق مطالعه کرد و در ادامه، رابطه کلی قضیه کار و انرژی و مفهوم آن مورد بررسی قرار گرفت. سپس اثبات قضیه کار و انرژی در دو حالت نیرو یکنواخت و متغیر، انجام شد و در نهایت با استفاده از چند مثال، شیوه استفاده از این قضیه در مسائل گوناگون مورد بررسی قرار گرفت.

در صورتی که به مباحث ارائه شده، علاقه‌مند هستید و قصد یادگیری در زمینه‌های مطرح شده در فیزیک پایه و مکانیک را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های فیزیک
• مجموعه آموزش‌های دروس مهندسی مکانیک
• آموزش فیزیک پایه ۱
• آیرودینامیک (Aerodynamics) چیست؟ — از صفر تا صد
• مرکز جرم (Centre of Mass) -- به زبان ساده
• پمپ‌ گریز از مرکز (Centrifugal Pump) — به زبان ساده
• قوانین حرکت نیوتن — به زبان ساده
• مومنتوم خطی (Linear Momentum) در سیالات — از صفر تا صد