سری تیلور — از صفر تا صد

هر معادله‌ای را می‌توان با استفاده از چند‍‌جمله‌ای از مرتبه بینهایت مدل‌سازی کرد. [منظور از بینهایت، چند‌جمله‌ای است که در آن بزرگ‌ترین توان متغیر بینهایت باشد.] به چنین رابطه‌ای «سری تیلور» (Taylor Series) گفته می‌شود. این سری کاربرد بسیاری در فیزیک کلاسیک، کوانتوم و ریاضیات دارد.

مقدمه

فرض کنید (f(x تابعی حقیقی است. سری تیلورِ این تابع حول نقطه x=x₀ به صورت زیر تعریف می‌شود.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

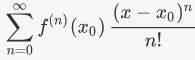
توجه داشته باشید که تابع (f(n)(x0، مشتق nام تابع (f(x در نقطه x=x₀ است. شاید در نگاه اول متوجه یک عبارت چند‌جمله‌ای از درجه بینهایت نشده باشید؛ بنابراین به منظور درک بهتر، قصد داریم تا در مثال اول، سری تیلور تابع f(x)=Cos x را حول نقطه x=0 بنویسیم. دقت کنید که الزامی جهت انتخاب نقطه x=0 وجود ندارد. دلیل این انتخاب، کاربردی بودن این نقطه در اکثر مسائل فیزیک و ریاضیات است.

حال با استفاده از تعریف کلی ارائه شده در بالا، شروع به نوشتن سری تیلور f(x)=Cos x حول نقطه x=0 می‌کنیم. همان‌طور که در فرمول بالا نیز نشان داده شده، به منظور بدست آوردن این سری، بایستی مشتق nام تابع (f(x در نقطه x=0 محاسبه شود. بنابراین این مشتقات در نقطه مدنظر عبارتند از:

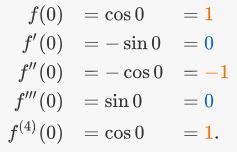
با توجه به فرمول کلی، جمله دوم این سری برابر است با:

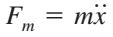
قبل از مطالعه ادامه مطلب در این مورد فکر کنید که جمله سوم و چهارم این سری به چه شکل هستند. بر مبنای فرمول کلی، این جملات به ترتیب به صورت زیر بدست می‌آیند.

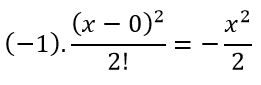
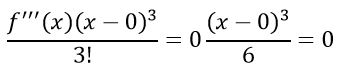
همان‌طور که دیدید چهار جمله اول این سری مشخص شدند؛ بنابراین سری تیلور تابع Cos x، برابر با حاصل جمع این جملات و به صورت زیر است.

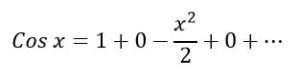
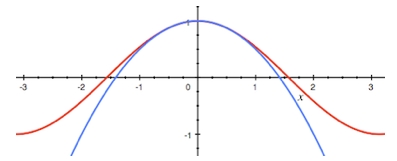
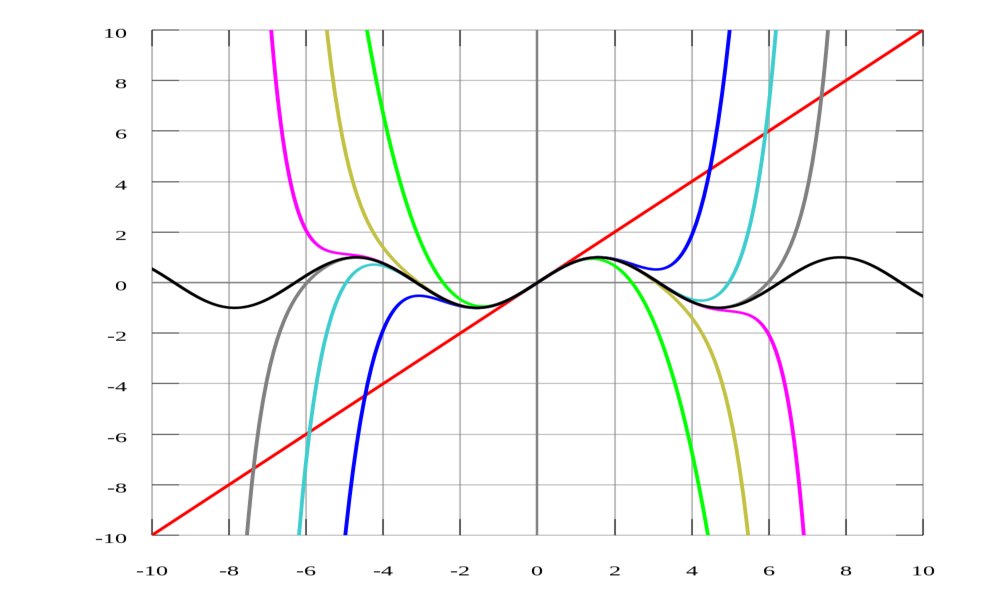
همان‌طور که در شکل بالا نیز دیده می‌شود نمودار قرمز رنگ نشان‌دهنده تابع cos x و نمودار آبی رنگ، سری همین تابع، اما تا سه جمله اول را نشان می‌دهد. دقت کنید که هر چه تعداد جملات در نظر گرفته‌ شده این سری، بیشتر باشند، مدل‌سازی تابع مد‌نظر نیز به خود تابع نزدیک‌تر خواهد بود. انیمیشن پایین توصیف بهتری را از این مفهوم نشان می‌دهد.

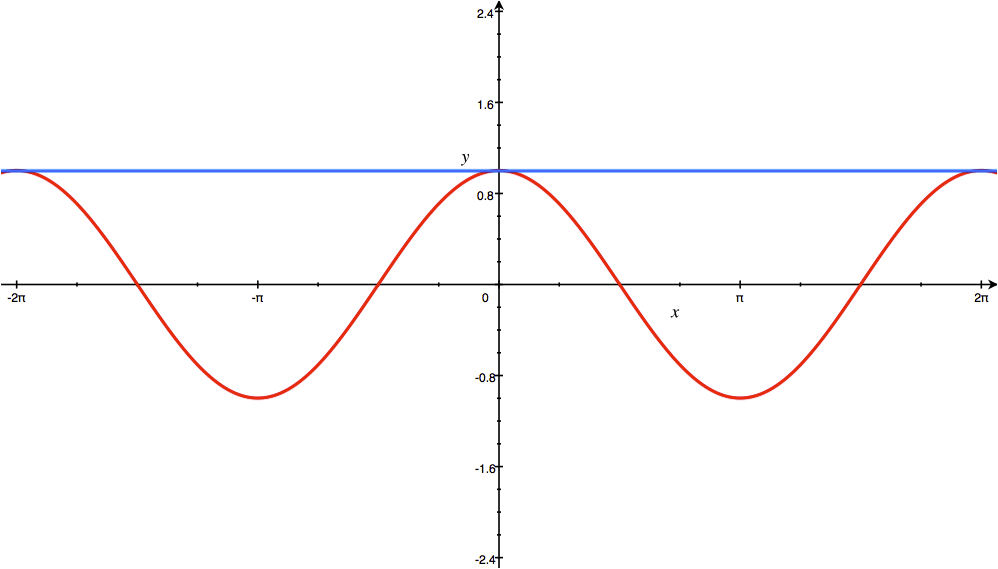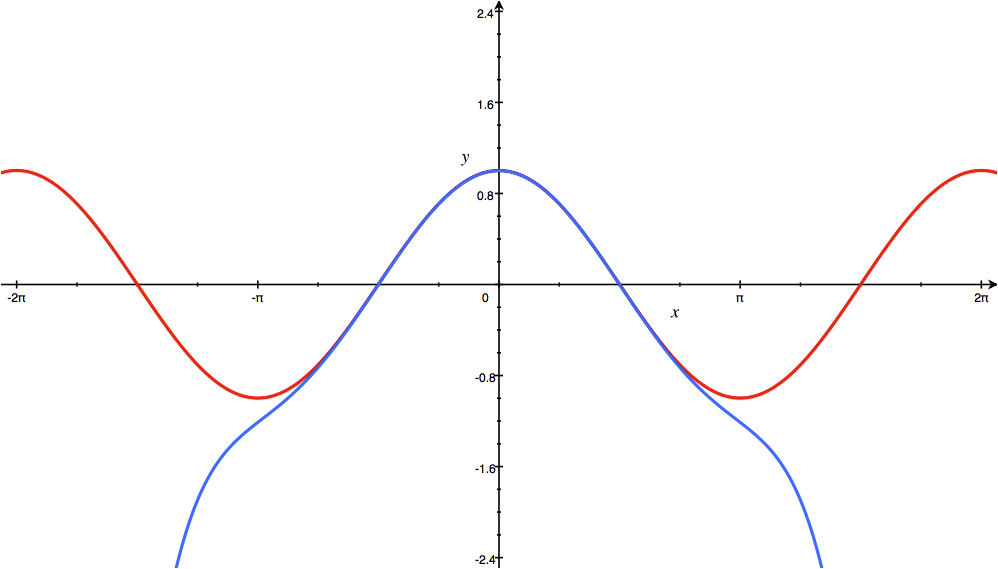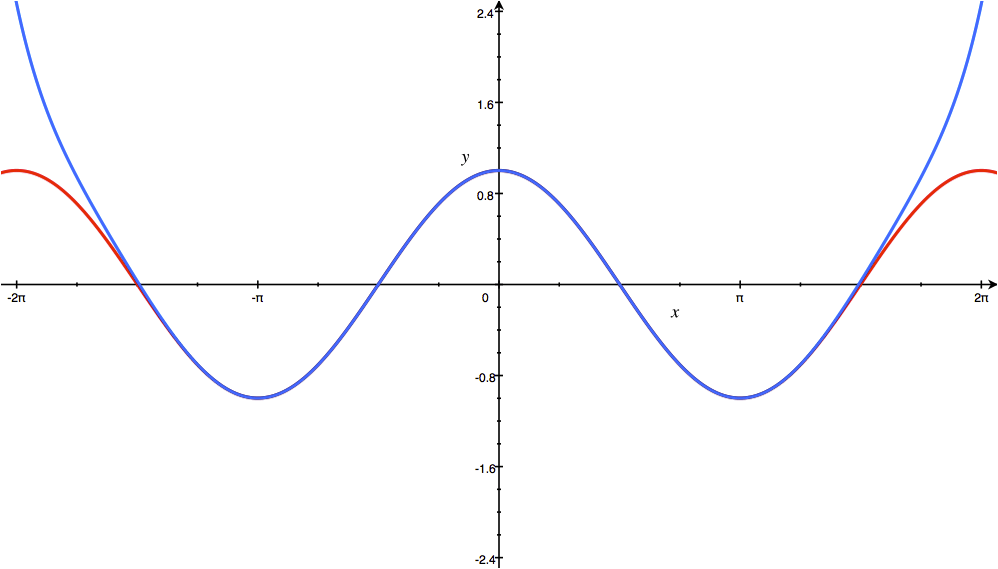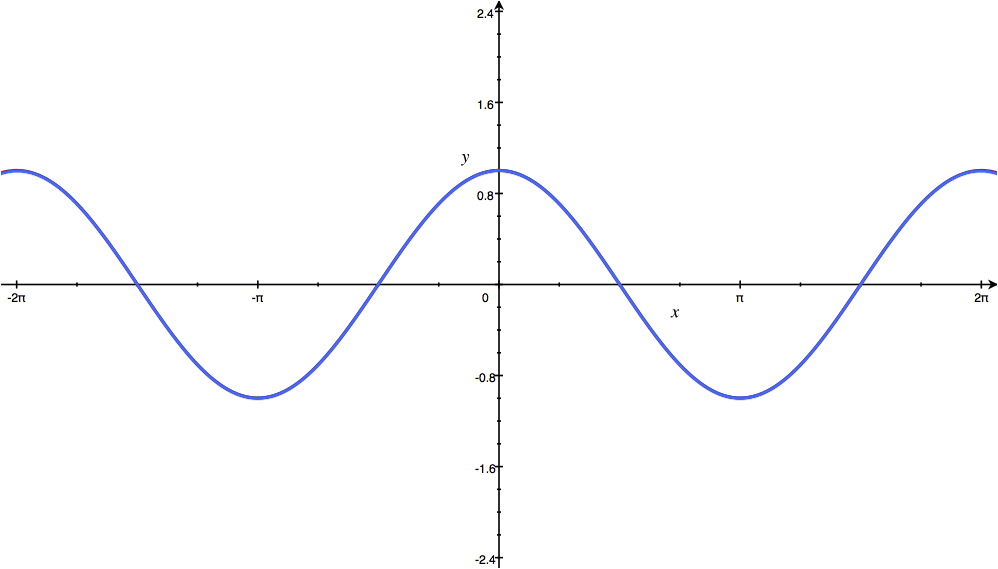
با افزایش جملات سری تیلور، نمودار آبی رنگ به تابع f(x)=Cos x (نمودار قرمز رنگ) نزدیک‎‌تر می‌شود.

معمولا در توابعی که به صورت «دوره‌ای» (Periodic) هستند، الگوی مشخصی برای سری تیلور قابل تعریف است. مثلا مشتقات فرد تابع y=Cos x در نقطه x=0، صفر هستند؛ بنابراین در سری این تابع، فقط توان‌های زوجِ x ظاهر خواهند شد. در عبارت زیر 4 جمله اول این سری ذکر شده است.

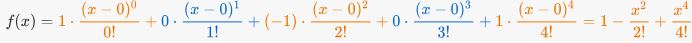
با توجه به الگوی مشاهده شده در بالا، تنها مشتقات زوج تابع Cos x در نظر گرفته می‌شوند. نهایتاً می‌توان سری تیلور تابع Cos x را به صورت زیر ذکر کرد.

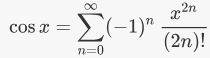
سری تیلوری که حول نقطه x=0 نوشته شود، «سری مکلورن» (Maclaurin Series) نامیده می‌شود.

در مثال دوم قصد داریم تا سری تیلور تابع y=Sin x را حول نقطه x=0 بدست آوریم. بدین منظور مشتقات اول تا چهارم این تابع، به صورت زیر محاسبه می‌شوند:

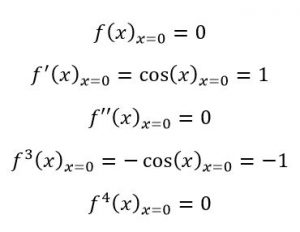
بنابراین با جایگذاری این مقادیر در رابطه کلی مربوط به سری تیلور، جملات اول آن حول نقطه x=0 به صورت زیر بدست می‌آیند.

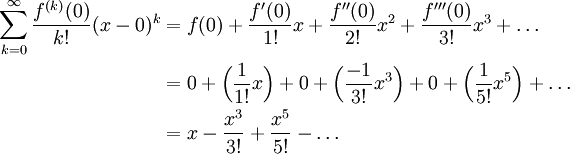
همان‌طور که در رابطه بالا نیز دیده می‌شود، برخلاف تابع y=Cos x تمامی جملات زوجِ سری y=Sin x صفر هستند. بنابراین شکل کلی بسط تیلور تابع Sin x برابر است با:

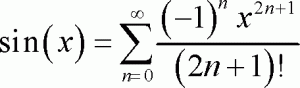
به همین صورت بسط تیلور تابع y=e^x را می‌توان به صورت زیر محاسبه کرد.

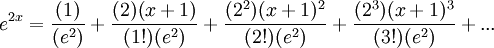
شعاع همگرایی

شعاع همگرایی در یک سری تیلور عبارت است از مقادیری از x که سری به ازای آن‌ها همگرا شود. یعنی این‌که به ازای چه مقادیری از x، سری تیلور نوشته شده به بینهایت میل نمی‌کند. به عنوان مثال سری تیلور تابع (y=1/(1-x به صورت زیر است.

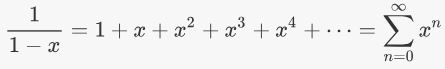
شکل سری نشان می‌دهد که به ازای x‌های کمتر از 1 و بیشتر از 1- همواره سری مذکور همگرا خواهد بود.

کاربرد سری تیلور

تصور کنید که یک زندانی هستید. نگهبان شما نیز فردی است که به ریاضیات علاقه‌مند است؛ بنابراین او به شما پیشنهاد می‌دهد که در صورت محاسبه مقدار $$\root 3 \of {8.1}$$

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

وی همچنین از شما خواسته، که مقدار محاسبه شده بایستی تا 5 رقم اعشار دقیق باشد. شما بدون استفاده از ماشین‌حساب و تنها با استفاده از چند جمله اول سری تیلور این تابع، قادر خواهید بود تا ریشه سوم 8.1 را محاسبه کنید.

در ابتدا بایستی سری تابع $$f(x)=\root 3 \of x$$

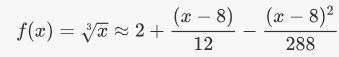
با جایگذاری 8.1 به جای x در سری بالا، می‌توان مقدار نسبتاً دقیقی از $$\root 3 \of {8.1}$$

نهایتاً تنها با نوشتن سه جمله اول بسط تیلور این رابطه، مقدار $$\root 3 \of {8.1}$$

اگر به مطالب مرتبط در زمینه ریاضیات علاقه‌مند هستید، احتمالا آموزش‌های زیر می‌تواند برایتان مفید باشد.

• جموعه ها در ریاضیات – مفاهیم پایه | فرادرس
• علائم هندسی در ریاضیات؛ مختصر و مفید
• آموزش ریاضیات عمومی ۱
• آموزش ریاضی عمومی ۲
• آموزش ریاضیات مهندسی (مرور – تست کنکور ارشد)

^^