آماره بسنده (Sufficient Statistic) و بسنده مینیمال — به زبان ساده

در تئوری آمار، موضوع برآوردیابی از اهمیت خاصی برخوردار است. منظور از برآوردیابی، بدست آوردن تابعی از نمونه تصادفی است که بتوان به کمک آن پارامتر جامعه را مشخص کرد. به نظر می‌رسد برای رسیدن به این منظور آماره نباید تابعی از پارامتر باشد. در این حالت فرض کنید $$T_n(X)$$ تابعی از نمونه تصادفی n تایی باشد، علاقمند هستیم که این آماره بتواند بیشترین اطلاعات را در مورد پارامتر مجهول جامعه در اختیارمان قرار دهد، بطوری که هر آماره دیگر، قادر به ارائه این میزان اطلاعات در مورد پارامتر نباشد. چنین تابعی از نمونه تصادفی را به عنوان «آماره بسنده» (Sufficient Statistic) می‌شناسیم.

به نظر می‌رسد بهترین پاسخ برای چنین وضعیتی می‌تواند خود نمونه تصادفی $$X_1,X_2, \cdots , X_n$$ باشد. ولی در بعضی از مواقع می‌توان توابعی دیگر مانند حاصل جمع یا میانگین نمونه تصادفی را هم به عنوان آماره بسنده برای پارامتر جامعه در نظر گرفت. به این ترتیب این آماره‌ها میزان اطلاعات یکسانی از پارامتر جامعه در خود دارند. همانطور که مشخص شد، آماره بسنده یکتا نیست و ممکن است آماره‌ها مختلفی پیدا کرد که در مورد پارامتر، اطلاعات یکسانی داشته باشند. به این منظور به دنبال آماره بسنده‌ای هستیم که بتواند همه آماره‌های بسنده دیگر را تحت پوشش قرار دهد. چنین آماره‌ای را «آماره بسنده مینیمال» (Minimal Sufficient Statistic) می‌نامیم.

در این نوشتار به معرفی و بررسی خصوصیات آماره بسنده و بسنده مینیمال خواهیم پرداخت و البته دستورالعمل‌هایی به منظور شناسایی آن ارائه خواهیم داد. به کمک آماره بسنده و بسنده مینیمال می‌توان ابعاد یک مسئله استنباط آماری را کوچک کرد و مثلا از میانگین به جای کل نمونه تصادفی برای برآورد پارامتر یا انجام آزمون فرض استفاده کرد. برای مطالعه بیشتر در زمینه برآوردگرها و برآوردگرهای فاصله‌ای به مطلب‌های تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده و فاصله اطمینان (Confidence Interval) — به زبان ساده مراجعه کنید. البته خواندن نوشتار آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات نیز خالی از لطف نیست.

آماره بسنده (Sufficient Statistic)

اگر $$X=\{X_1,X_2,\cdots,X_n\}$$ یک نمونه تصادفی مستقل و هم توزیع با توجه به پارامتر ثابت ولی ناشناخته $$\theta$$ باشد، آماره بسنده را به صورت $$T(X)$$ نشان داده که تابعی از نمونه تصادفی محسوب شده و شامل بیشترین اطلاعاتی است که برای برآورد پارامتر $$\theta$$ لازم است.

فیلم آموزش آمار ریاضی ۱ – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

مفهوم و تعریف اولیه برای آماره بسنده توسط دانشمند بزرگ آمار «رونالد فیشر» (Ronald Fisher) در سال ۱۹۲۰ ارائه شد. این تعریف بعدها به عنوان یک مبنا برای شناسایی آماره‌های مناسب به منظور برآورد پارامتر نامعلوم جامعه بدل شد. در ادامه پژوهش‌های فیشر، قضیه‌هایی که برمبنای آماره بسنده ساخته شده (مانند قضیه Rao-Blackwell)، روش‌هایی برای ایجاد بهترین برآوردگرها (با کمترین واریانس) در کلاس برآوردگرهای نااریب معرفی شد که همه مرهون تحقیقات فیشر در این زمینه بودند.

تعریف رسمی آماره بسنده

با توجه به اطلاعاتی که از احتمال شرطی یا توزیع شرطی در دیگر مطالب فرادرس داریم، می‌توانیم تعریف رسمی برای آماره بسنده را به صورت زیر بیان کنیم.

آماره $$T(X)$$ بسنده برای پارامتر $$\theta$$ است اگر توزیع احتمال نمونه تصادفی به شرط آماره $$T(X)$$ مستقل از پارامتر $$\theta$$ باشد. 

این گزاره نشان می‌دهد که اگر آماره بسنده در اختیارمان باشد، برای محاسبه تابع احتمال نمونه تصادفی دیگر احتیاجی به پارامتر نیست و اطلاعاتی که $$T(X)$$ در خود دارد می‌تواند جایگزین پارامتر برای محاسبه احتمال شود.

مثال 1

فرض کنید $$X_1$$ و $$X_2$$ دو متغیر تصادفی (یک نمونه دو تایی) از توزیع برنولی با پارامتر $$p$$ باشند. در این صورت مشاهدات ما از این دو متغیر تصادفی به صورت زوج مرتب و به شکل زیر نوشته می‌شوند.

$$\large \chi =\{(0,0),(0,1),(1,0),(1,1)\}$$

فرض کنید در این میان $$T(X)=X_1+X_2$$ آماره بسنده باشد. باید مطابق تعریفی که از آماره بسنده داشتیم تابع احتمال شرطی نمونه تصادفی به شرط $$T(X)$$ شامل پارامتر $$p$$‌ نباشد. می‌دانیم مجموع دو متغیر تصادفی برنولی مستقل و هم توزیع (با پارامتر $$p$$) دارای توزیع دو جمله‌ای با پارامترهای 2 و $$p$$ است.

$$\large T(X)=X-1+X_2 \sim B(2,p)$$

بنابراین می‌توان تابع احتمال آن‌ها را به صورت زیر نمایش داد.

$$\large P(T(X))=P(X_1+X_2=x)={2 \choose x}p^x(1-p)^{(2-x)},\;\;x=0,1,2$$

حال احتمال شرطی نمونه تصادفی را به شرط آماره بسنده محاسبه می‌کنیم.

$$\large P(X_1=x_1,X_2=x_2|T(X))=P(X_1=x_1, X_2=x_2|X_1+X_2=x)$$

همانطور که می‌بینید این احتمال شبیه تابع درستنمایی است که برحسب آماره بسنده شرطی شده است. اطلاع دارید که تابع درستنمایی نیز از ابتکارات و ابداعات دانشمند بزرگ «رونالد فیشر» است. در ادامه محاسبات مربوط به رابطه بالا را پی می‌گیریم.

$$\large= \begin{cases} 0& x\neq x_1+x_2\\ \large \dfrac{p^{x_1}(1-p)^{(1-x_1)}p^{x_2}(1-p)^{(1-x_2)}}{{2 \choose x}}&x=x_1+x_2\end{cases}\\ \large= \begin{cases} 0& x\neq x_1+x_2\\ \large \dfrac{p^{x_1+x_2}(1-p)^{(1-x_1+1-x_2)}}{{2 \choose x}} & x =x_1+x_2\end{cases}\\ \large= \begin{cases} 0& x\neq x_1+x_2\\ \large \dfrac{p^{x}(1-p)^{(2-x)}}{{2 \choose x}p^{x}(1-p)^{(2-x)}} & x =x_1+x_2 \end{cases}\\ \large = \begin{cases} 0& x\neq x_1+x_2\\ \large \dfrac{1}{{2 \choose x}} & x =x_1+x_2 \end{cases}$$

همانطور که دیده می‌شود، تابع احتمال شرطی وابسته به پارامتر $$\theta$$ نیست. بنابراین $$T(X)=X_1+X_2$$ به درستی به عنوان آماره بسنده انتخاب شده است.

قضیه فاکتورگیری فیشر-نیمن (Fisher-Neyman Factorization Theorem)

فرض کنید $$X$$ نمونه‌ای تصادفی مستقل و هم توزیع با پارامتر $$\theta$$ باشند. می‌توان نشان داد که توزیع توام این نمونه تصادفی برحسب آماره بسنده $$T(X)$$ به صورت زیر قابل تفکیک است:

$$\large f_X(x)=h(x)g(\theta,T(x))$$

در رابطه بالا $$h(x)$$ تابعی از نمونه تصادفی است که شامل پارامتر جامعه نیست و از طرفی دیگر $$g(\theta,T(x))$$ تابعی نامنفی از نمونه تصادفی و پارامتر جامعه است.

فیلم آموزش آمار و احتمالات مهندسی – حل نمونه سوالات کنکور ارشد در فرادرس

کلیک کنید

به این ترتیب می‌توان گفت که تابع احتمال را می‌توان به دو بخش تقسیم کرد. بخشی که فقط وابسته به نمونه تصادفی یعنی $$X$$ است و بخشی که به صورت ترکیبی از نمونه تصادفی و پارامتر جامعه است. در اینجا $$T(X)$$ آماره بسنده نامیده می‌شود. این قضیه با نام تفکیک یا «فاکتورگیری فیشر-نیمن» (Fisher-Neyman Factorization Theorem) معروف است.

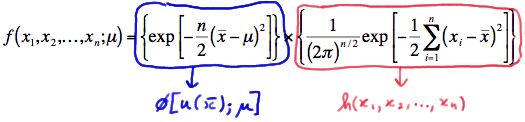
با توجه به این قضیه مشخص است که نمونه تصادفی $$X$$ خود یک آماره بسنده محسوب می‌شود. در بیشتر مواقع برای پیدا کردن آماره بسنده از این قضیه استفاده می‌شود زیرا تعریف ارائه شده برای آماره بسنده، روشی برای پیدا کردن آن مشخص نمی‌کند و فقط شرایطی که یک آماره را بسنده می‌کند، در تعریف مطرح شده است.

نکته: اگر $$T(X)$$ آماره بسنده باشد، به راحتی با استفاده از این قضیه می‌توان نشان داد به ازاء مقدار ثابت غیر صفر $$c$$، هر تابعی مثل $$T^*(X)=cT(X)$$ نیز آماره بسنده است. بنابراین آماره بسنده یکتا نیست. ولی می‌دانیم مقدار اطلاعاتی که $$T(X)$$ و $$T^*(X)$$‌ در مورد پارامتر به همراه دارند یکسان است. در غیر اینصورت آماره بسنده محسوب نمی‌شدند.

مثال 2

فرض کنید می‌خواهیم برای توزیع نمایی با پارامتر $$\theta$$، آماره بسنده پیدا کنیم. به این منظور نمونه تصادفی n تایی به صورت $$X_1, X_2, \cdots X_n$$ تهیه کرده‌ایم. طبق قضیه فاکتورگیری فیشر- نیمن عمل می‌کنیم.

از آنجایی که این نمونه تصادفی مستقل و هم توزیع (iid) هستند می‌توانیم آن‌ها را به صورت  $$X_{1}^{n}=(X_{1},\dots ,X_{n})$$ نشان دهیم. با توجه به تابع احتمال این متغیرهای تصادفی، توزیع احتمال توام (همزمان) آن‌ها به صورت زیر نوشته می‌شود.

$$\large {\displaystyle {\begin{aligned}f_{X_{1}^{n}}(x_{1}^{n})&=\prod _{i=1}^{n}{1 \over \theta }\,e^{{-1 \over \theta }x_{i}}={1 \over \theta ^{n}}\,e^{{-1 \over \theta }\sum _{i=1}^{n}x_{i}}\end{aligned}}}$$

حال می‌توانید طبق قضیه فاکتورگیری توابع $$h(X)$$ و $$g(\theta, T(X))$$ را به صورت زیر در نظر گرفت.

$$\large {\begin{aligned}h(x_{1}^{n})=1,\,\,\,g(\theta,x_{1}^{n})={1 \over \theta ^{n}}\,e^{{-1 \over \theta }\sum _{i=1}^{n}x_{i}}\end{aligned}}$$

مشخص است که $$h$$ فقط به نمونه تصادفی و $$g$$ نیز به پارامتر و نمونه تصادفی از طریق $$\sum_{i=1}^nX_i$$ وابسته است، بنابراین می‌توان آماره بسنده را $$T(X)= \sum_{i=1}^nX_i$$ در نظر گرفت.

مثال 3

فرض کنید $$X_1, X_2, \cdots X_n$$ نمونه تصادفی مستقل و هم‌توزیع از نرمال با میانگین نامعلوم $$\theta$$ و واریانس معلوم $$\sigma^2$$ باشند. نشان می‌دهیم که میانگین نمونه‌ای، آماره بسنده برای میانگین جامعه $$\theta$$ محسوب می‌شود.

توزیع توام این نمونه تصادفی را با توجه به توزیع نرمال به صورت زیر می‌نویسیم. طی مراحلی که در ادامه قابل مشاهده است، از قضیه فاکتورگیری به این نتیجه می‌رسیم که میانگین نمونه‌ای، آماره بسنده برای میانگین جامعه $$\theta$$ است.

$$\large {\displaystyle {\begin{aligned}f_{X_{1}^{n}}(x_{1}^{n})&=\prod _{i=1}^{n}{\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \left(-{\frac {(x_{i}-\theta )^{2}}{2\sigma ^{2}}}\right)\\&=(2\pi \sigma ^{2})^{-{\frac {n}{2}}}\exp \left(-\sum _{i=1}^{n}{\frac {(x_{i}-\theta )^{2}}{2\sigma ^{2}}}\right)\\&=(2\pi \sigma ^{2})^{-{\frac {n}{2}}}\exp \left(-\sum _{i=1}^{n}{\frac {\left(\left(x_{i}-{\overline {x}}\right)-\left(\theta -{\overline {x}}\right)\right)^{2}}{2\sigma ^{2}}}\right)\\&=(2\pi \sigma ^{2})^{-{\frac {n}{2}}}\exp \left(-{1 \over 2\sigma ^{2}}\left(\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}+\sum _{i=1}^{n}(\theta -{\overline {x}})^{2}-2\sum _{i=1}^{n}(x_{i}-{\overline {x}})(\theta -{\overline {x}})\right)\right)\\&=(2\pi \sigma ^{2})^{-{\frac {n}{2}}}\exp \left(-{1 \over 2\sigma ^{2}}\left(\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}+n(\theta -{\overline {x}})^{2}\right)\right)\end{aligned}}}$$

با توجه به رابطه $$\sum _{i=1}^{n}(x_{i}-{\overline {x}})(\theta -{\overline {x}})=0$$ می‌توان محاسبات قبل را به صورتی که در ادامه قابل مشاهده است ساده‌تر کرد.

$$\large \begin{aligned} (2\pi \sigma ^{2})^{-{\frac {n}{2}}}\exp \left(-{1 \over 2\sigma ^{2}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\right)\exp \left(-{\frac {n}{2\sigma ^{2}}}(\theta -{\overline {x}})^{2}\right) \end{aligned}$$

بنابراین تابع $$h$$ و $$g$$ به صورت زیر نوشته خواهند شد.

$$\large {\displaystyle {\begin{aligned}h(x_{1}^{n})&=(2\pi \sigma ^{2})^{-{\frac {n}{2}}}\exp \left(-{1 \over 2\sigma ^{2}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\right)\\ \large g(\theta,x_{1}^{n})&=\exp \left(-{\frac {n}{2\sigma ^{2}}}(\theta -{\overline {x}})^{2}\right)\end{aligned}}}$$

به این ترتیب مشخص است که تابع $$g$$ از طریق $$\overline{x}$$ به نمونه تصادفی مرتبط است. بنابراین میانگین نمونه‌ای $$\overline{X}$$، آماره بسنده برای پارامتر میانگین جامعه محسوب می‌شود.

$$\large {\displaystyle T(X_{1}^{n})={\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}}$$

آماره بسنده مینیمال

همانطور که در مطالب قبل گفته شد، آماره بسنده یکتا نیست. بنا به تعریف، آماره بسنده‌ای که تابعی از همه آماره‌های بسنده باشد، بسنده مینیمال (Minimal Sufficient) نامیده می‌شود. به این ترتیب می‌توان آماره بسنده مینیمال را به نوعی موثرترین آماره بسنده برای پارامتر جامعه $$\theta$$ در نظر گرفت که عین اینکه بیشترین اطلاعات را به همراه دارد، از همه آماره‌های بسنده نیز خلاصه‌تر و ساده‌تر است.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

به طور رسمی آماره بسنده مینیمال را به صورت زیر تعریف می‌کنند.

آماره بسنده $$S(X)$$ را بسنده مینیمال می‌نامند اگر برای هر آماره بسنده دیگر مثل $$T(X)$$ و تابع دلخواه $$f$$ داشته باشیم:

$$\large S(X)=f(T(X))$$

برای مشخص کردن آماره بسنده از قضیه فاکتورگیری فیشر استفاده می‌کنیم. به این ترتیب اگر $$S(X)$$ آماره بسنده مینیمال باشد باید در رابطه زیر به صورت دو طرفه برقرار باشد.

$${\frac {f_{\theta }(x)}{f_{\theta }(y)}}\; is\; independent\; of\;\theta : \Longleftrightarrow S(x) = S(y)$$

این رابطه به این معنی است که اگر نسبت توابع توزیع توام دو نمونه تصادفی $$x$$ و $$y$$ بستگی به پارامتر $$\theta$$ نداشته باشد، بتوان نتیجه گرفت که آماره بسنده $$S$$ برای هر دو نمونه تصادفی یکسان است و البته برعکس. با این کار می‌توان بررسی کرد آیا یک آماره بسنده، می‌تواند بسنده مینیمال هم باشد یا خیر. این روش به نام قضیه «لهمن-شفه» (Lehmann–Scheffé theorem) معروف است.

به منظور روشن‌تر شدن موضوع به بررسی دو مثال می‌پردازیم.

مثال 4

فرض کنید $$X_1$$ و $$X_2$$ دو متغیر تصادفی (یک نمونه دو تایی) از توزیع برنولی با پارامتر $$p$$ باشند. در این صورت میانگین این دو آماره بسنده مینیمال است.

برای نشان دادن این موضوع کمی به عقب برمی‌گردیم. مطابق با مثال ۱ می‌دانیم مجموع این دو متغیر تصادفی، آماره بسنده است. برای سنجش صحت گزاره مثال ۴، کافی است نشان دهیم رابطه بالا برای این آماره بسنده برقرار است و می‌توان آن را به عنوان آماره بسنده مینیمال در نظر گرفت. با توجه به مثال ۱، تابع احتمال توام این نمونه تصادفی به صورت زیر است.

$$\large f_{p}(x_1,x_2)=P(X_1=x_1,X_2=x_2)= p^{x_1}(1-p)^{(1-x_1)}p^{x_2}(1-p)^{(1-x_2)}\\\large =p^{x_1+x_2}(1-p)^{(2-(x_1+x_2))}$$

با توجه به تعریف ارائه شده برای آماره بسنده مینیمال،اگر $$y_1$$ و $$y_2$$ دو نمونه تصادفی دیگر باشند خواهیم داشت:

$$\large \dfrac{f_{p}(x_1,x_2)}{f_{p}(y_1,y_2)}=\dfrac{p^{x_1+x_2}(1-p)^{(2-(x_1+x_2))}}{p^{y_1+y_2}(1-p)^{(2-(y_1+y_2))}}$$

برای آنکه طرف راست این تساوی به پارامتر $$p$$ بستگی نداشته باشد باید $$S(x_1,x_2)=x_1+x_2=y_1+y_2=s(y_1,y_2)$$ باشد و اگر این تساوی برقرار باشد، نسبت بالا به $$p$$ بستگی ندارد. بنابراین مجموع این دو متغیر تصادفی آماره بسنده مینیمال است.

نکته: آماره بسنده مینیمال نیز یکتا نیست. ولی اگر دو آماره بسنده مینیمال برای پارامتر جامعه ($$\theta$$) وجود داشته باشد، مطمئن هستیم که بینشان یک تابع یا رابطه یک به یک برقرار است. به این ترتیب می‌توان میانگین این دو متغیر تصادفی ($$\dfrac{X_1+X_2}{2}$$) را هم به عنوان آماره بسنده مینیمال در نظر گرفت.

مثال ۵

فرض کنید $$X_1, X_2, \cdots X_n$$ نمونه تصادفی مستقل و هم‌توزیع از نرمال با میانگین نامعلوم $$\theta$$ و واریانس معلوم $$\sigma^2$$ باشند. نشان می‌دهیم که میانگین نمونه‌ای، آماره بسنده مینیمال برای میانگین جامعه $$\theta$$ محسوب می‌شود.

مطابق با مثال ۳ می‌دانیم که تابع چگالی احتمال توام این نمونه تصادفی به صورت زیر نوشته می‌شود.

$$\large f(X;\theta)=\begin{aligned} (2\pi \sigma ^{2})^{-{\frac {n}{2}}}\exp \left(-{1 \over 2\sigma ^{2}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\right)\exp \left(-{\frac {n}{2\sigma ^{2}}}(\theta -{\overline {x}})^{2}\right) \end{aligned}$$

حال اگر نمونه تصادفی دیگری مانند $$Y_1,Y_2, \cdots Y_n$$ در نظر بگیریم با استفاده از قضیه لهمن-شفه خواهیم داشت:

$$\large \dfrac{f(X;\theta)}{f(Y;\theta)}=\dfrac{(2\pi \sigma ^{2})^{-{\frac {n}{2}}}\exp \left(-{1 \over 2\sigma ^{2}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\right)\exp \left(-{\frac {n}{2\sigma ^{2}}}(\theta -{\overline {x}})^{2}\right)}{(2\pi \sigma ^{2})^{-{\frac {n}{2}}}\exp \left(-{1 \over 2\sigma ^{2}}\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}\right)\exp \left(-{\frac {n}{2\sigma ^{2}}}(\theta -{\overline {y}})^{2}\right)}$$

برای آنکه این نسبت به پارامتر $$\theta$$ بستگی نداشته باشد باید داشته باشیم:

$$\large \dfrac{(\theta -{\overline {x}})^{2}}{(\theta -{\overline {y}})^{2}}=1\rightarrow \overline{x}=\overline{y}$$

در نتیجه $$\overline{X}$$ آماره بسنده مینیمال است.

نکته: اغلب آماره بسنده‌ای که از طریق فاکتورگیری فیشر ساخته می‌شود، بسنده مینیمال نیز هست.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های نرم‌افزارهای آماری
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده
• احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه

^^