تحلیل تنش-کرنش — آشنایی با مفاهیم و روش های اجرای تحلیل تنش

«تحلیل تنش-کرنش» (Stress-Strain Analysis)، یکی از شاخه‌های علم مهندسی است. در تحلیل تنش-کرنش یا به طور خلاصه تحلیل تنش، از روش‌های متعددی برای تعیین وضعیت تنش و کرنش درون مواد و سازه‌های تحت نیرو استفاده می‌شود. در مکانیک محیط‌های پیوسته، تنش یک کمیت فیزیکی به حساب می‌آید که شرایط نیروهای داخلی اعمال شده توسط ذرات مجاور درون یک ماده پیوسته را نشان می‌دهد. کرنش نیز معیاری برای بیان تغییر شکل ماده است.

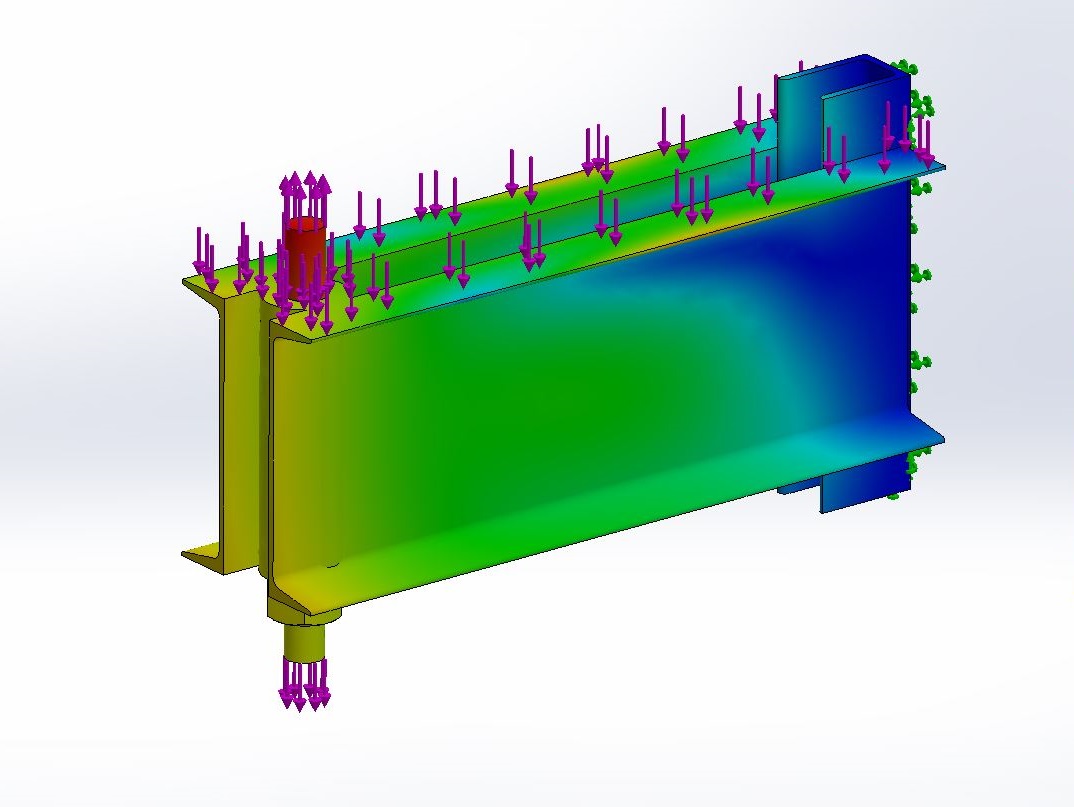
تحلیل تنش، یکی از اقدامات اولیه برای شروع فرآیند محاسبات در مهندسی عمران، مکانیک، هوافضا و ... محسوب می‌شود. این تحلیل نقش مهمی در طراحی سازه‌های مختلف از قبیل تونل‌ها، پل‌ها، سدها، قطعات موشک و هواپیما، قطعات مکانیکی و حتی لوازم خانگی و تجهیزات اداری دارد. به علاوه، به منظور نگهداری این سازه‌ها و پیش‌بینی عوامل تخریب یا شکست آن‌ها نیز از تحلیل تنش استفاده می‌شود.

معمولاً برای شروع یک تحلیل تنش باید موارد زیر را در نظر گرفت:

• مشخصات هندسی سازه مورد نظر
• خواص مواد به کار رفته در قطعات سازه
• نحوه اتصال اجزای مختلف سازه به یکدیگر
• حداکثر نیروی مورد انتظار یا نیروهای تعیین شده برای شرایط عادی

خروجی تحلیل تنش معمولاً به صورت مقادیر کمی است. این مقادیر نحوه توزیع نیرو، تنش، کرنش یا خمش‌های ایجاد شده درون کل سازه و هر یک از اجزای آن را توصیف می‌کنند. در این تحلیل، امکان در نظر گرفتن نیروهای وابسته به زمان مانند لرزش‌های موتور یا بار ناشی از حرکت وسایل نقلیه نیز وجود دارد. در چنین مواردی، تنش و تغییر شکل تابعی از زمان و مکان خواهند بود.

در علوم مهندسی، تحلیل تنش اغلب به عنوان ابزاری برای رسیدن به یک هدف نهایی در نظر گرفته می‌شود. این هدف، به کارگیری حداقل مواد مورد نیاز یا در نظر گرفتن معیارهای دیگر برای طراحی سازه‌هایی با قابلیت تحمل بارگذاری‌های از پیش تعیین شده است. برای اجرای تحلیل تنش می‌توان از روش‌های ریاضی، مدل‌های تحلیلی، شبیه‌سازی‌های کامپیوتری، آزمایش‌های تجربی یا ترکیبی از این موارد استفاده کرد.

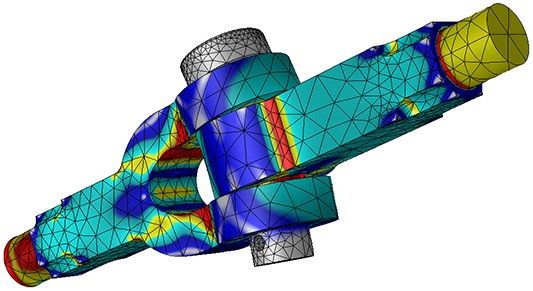
عبارت تحلیل تنش در این مقاله به منظور رعایت خلاصه‌نویسی به کار برده می‌شود. با این وجود، باید در نظر داشته باشید که بررسی کرنش و تغییر شکل سازه‌ها، اهمیت یکسانی با بررسی تنش دارد. در واقع، ممکن است که تحلیل یک سازه با محاسبه تغییر شکل یا کرنش‌های موجود در آن شروع شود و تنش، در مرحله آخر مورد ارزیابی قرار گیرد.

مبانی و کاربرد تحلیل تنش

تحلیل تنش به طور خاص برای مواد جامد به کار می‌رود و مطالعه تنش در مایعات و گازها به حوزه مکانیک سیالات مربوط می‌شود. در این تحلیل، خواص مواد در حوزه مکانیک محیط‌های پیوسته (خواص همگن در مقیاس‌های کوچک) از دیدگاه ماکروسکوپی مورد بررسی قرار می‌گیرد. بنابراین، حتی کوچک‌ترین ذرات مورد بررسی در تحلیل تنش نیز دارای تعداد بسیار زیادی اتم خواهند بود. در واقع، خواص این ذرات، میانگین خواص تمام اتم‌های تشکیل‌دهنده آن‌ها است.

در تحلیل تنش ممکن است عوارض فیزیکی ناشی از اعمال نیرو یا ماهیت دقیق ماده نادیده گرفته شود. در مقابل، معمولاً فرض می‌شود که رابطه بین تنش‌ها و کرنش درون ماده از یک سری معادلات مشخصه معین پیروی می‌کند.

طبق قوانین حرکتی نیوتن، تمام نیروهای خارجی اعمال شده به یک سیستم، یا باید توسط عکس‌العمل نیروهای داخلی خنثی شوند و یا ذرات تحت تأثیر را به حرکت درآورند. در مواد جامد، حرکت تمام ذرات باید به صورت هماهنگ و در جهت حفظ شکل کلی جسم صورت گیرد. به این ترتیب، نیروی اعمال شده به بخشی از جسم باعث افزایش نیروهای عکس‌العمل داخلی می‌شود و از ذره‌ای به ذره دیگر در محدوده بزرگ‌تری از سیستم انتشار می‌یابد. دلیل ایجاد نیروهای داخلی در اکثر مواد (به جز مواد فرو مغناطیس و اجسام بزرگ در مقیاس یک سیاره)، برهم‌کنش‌های بین مولکولی در محدوده‌های بسیار کوچک است. این نیروهای داخلی خود را به صورت نیروهایی بین سطوح اتصال ذرات مجاور درون ماده نشان می‌دهند و به عنوان تنش شناخته می‌شود.

مسئله اصلی در تحلیل تنش

مسئله اصلی در تحلیل تنش، تعیین توزیع تنش‌های داخلی یک سیستم در حین اعمال نیروهای خارجی با مقادیر مشخص است. در اصل، این مسئله به تعیین مستقیم یا غیر مستقیم «تانسور تنش کوشی» (Cauchy Stress Tensor) در هر نقطه از جسم ختم می‌شود.

نیروهای خارجی را می‌توان به دو دسته زیر تقسیم‌بندی کرد:

1. نیروهای جسمی: نیروهایی نظیر جاذبه مغناطیسی یا نیروی ثقل که درون جسم اعمال می‌شوند.
2. بارهای متمرکز: نیروهایی مانند اصطکاک بین محور و یاتاقان یا وزن چرخ‌های قطار بر روی ریل که می‌توان نحوه اعمال آن‌ها را به صورت دوبعدی، در امتداد یک خط یا حتی بر روی یک نقطه در نظر گرفت.

توجه: تأثیر نیروهای خارجی بر روی تنش محلی درون جسم به نحوه اعمال آن‌ها (به صورت گسترده یا متمرکز) بستگی دارد.

وضعیت انواع سازه‌ها در علوم مهندسی

در مسائل مرتبط با مهندسی عمران، معمولاً سازه‌ها را در حالت تعادل استاتیکی در نظر می‌گیرند. در این وضعیت، یا با گذشت زمان هیچ تغییری در سیستم رخ نمی‌دهد یا تغییرات به اندازه‌ای آرام هستند که اهمیتی برای تنش‌های ویسکوز ندارند (حالت شبه استاتیک). در مسائل مربوط به مهندسی مکانیک و هوافضا، در اغلب موارد تحلیل تنش بر روی قطعاتی انجام می‌شود که وضعیت آن‌ها فاصله زیادی از حالت تعادل استاتیکی دارد. صفحات در حال لرزش یا چرخ‌ها و محورهای در حال چرخش را در نظر بگیرید. در این موارد، باید شتاب ذرات در معادله حرکت در نظر گرفته شود. در مسائل مربوط به طراحی سازه، طراحان معمولاً از پایین بودن مقدار تنش موجود در تمام اجزای سازه نسبت به مقاومت تسلیم اطمینان حاصل می‌کنند. در صورت وجود بارهای دینامیکی، خستگی ماده نیز در نظر گرفته می‌شود. با این وجود، این موارد خارج از حوزه تحلیل تنش هستند و در بخش‌های دیگر علم مواد تحت عناوینی نظیر «مقاومت مصالح» (Strength of Materials)، «تحلیل خستگی» (Fatigue Analysis)، «خوردگی تنشی» (Stress Corrosion)، «مدل‌سازی خزش» (Creep Modeling) و غیره پوشش داده می‌شوند.

روش‌های آزمایشگاهی اجرای تحلیل تنش

یکی از روش‌های اجرای تحلیل تنش، اعمال نیرو به یک نمونه آزمایشگاهی یا یک سازه و سپس اندازه‌گیری تنش‌های به وجود آمده با استفاده از حسگرهای مخصوص است. این فرآیند، اجرای آزمایش (مخرب یا غیر مخرب) نام دارد.

روش‌های آزمایشگاهی معمولاً در صورت دشوار بودن یا دقت پایین رویکردهای ریاضی مورد استفاده قرار می‌گیرند. به منظور اعمال بارگذاری‌های استاتیک یا دینامیک در روش‌های آزمایشگاهی به تجهیزات مخصوص برای هر آزمایش نیاز است. در ادامه، چند روش آزمایشگاهی مورد استفاده در فرآیند تحلیل تنش را معرفی می‌کنیم:

«آزمایش کششی» (Tensile Test)، یکی از آزمایش‌های اصلی در علم مواد است که در طی آن، نمونه‌ای را تحت کشش تک‌محوری قرار می‌دهند. اعمال کشش تا زمان رخ دادن شکست در نمونه ادامه می‌یابد. نتایج به دست آمده از این آزمایش معمولاً برای انتخاب مواد برای ساخت سازه‌های مختلف، کنترل کیفیت یا پیش‌بینی رفتار مواد تحت انواع مختلف بارگذاری مورد استفاده قرار می‌گیرند. در آزمایش کششی، امکان اندازه‌گیری مستقیم خواصی نظیر مقاومت کششی نهایی، کشیدگی ماکسیمم و کاهش مساحت سطح مقطع وجود دارد. در نهایت، با به دست آوردن این خواص می‌توان خصوصیاتی مانند مدول یانگ، نسبت پواسون، مقاومت تسلیم و سخت‌شوندگی کرنش نمونه را تعیین کرد.

«کرنش‌سنج» (Strain gauge)، وسیله‌ای است که برای تعیین تغییر شکل قطعات فیزیکی در حین آزمایش مورد استفاده قرار می‌گیرد. متداول‌ترین نوع کرنش‌سنج، یک مقاومت نازک و مسطح است که به سطح قطعه مورد آزمایش چسبانده می‌شود و کرنش را در جهت مورد نظر اندازه‌گیری می‌کند. با اندازه‌گیری کرنش در امتداد سه جهت بر روی یک سطح می‌توان حالت تنش موجود در قطعه مورد آزمایش را محاسبه کرد.

«پراش نوترونی» (Neutron Diffraction)، یکی از روش‌های مورد استفاده برای تعیین کرنش زیرسطحی در قطعات مورد آزمایش است.

«روش فتوالاستیک» (Photoelastic Method)، بر پایه خاصیت دوشکستی برخی از مواد در هنگام اعمال تنش بنا شده است. در این مواد، مقدار انکسار در هر نقطه به حالت تنش در آن نقطه بستگی دارد. تنش‌های موجود در یک سازه را می‌توان با ایجاد یک مدل از جنس مواد فتوالاستیک تعیین کرد.

«تحلیل مکانیکی دینامیکی» (Dynamic Mechanical Analysis) یا اصطلاحاً «DMA»، روشی برای مطالعه و تعیین خواص مواد ویسکوالاستیک، بخصوص پلیمرها است. در این تحلیل، با اعمال نیروی سینوسی (تنش) به مواد مورد نظر و اندازه‌گیری جابجایی ناشی از اعمال نیرو (کرنش)، خاصیت ویسکوالاستیک پلیمرها مورد مطالعه قرار می‌گیرد. در جامدات کاملاً الاستیک، تنش و کرنش ایجاد شده به طور کامل در یک فاز مشترک قرار دارند. در سیالات کاملاً ویسکوز، یک تأخیر فاز 90 درجه‌ای بین تنش و کرنش دیده می‌شود. پلیمرهای ویسکوالاستیک بین دو مورد قبلی قرار می‌گیرند و در حین آزمایش DMA مقداری تأخیر فاز خواهند داشت.

روش‌های ریاضی برای اجرای تحلیل تنش

روش‌های آزمایشگاهی کاربرد گسترده‌ای در انجام تحلیل‌های تنش دارند. با این وجود، اکثر این تحلیل‌ها با استفاده از روش‌های ریاضی و در حین طراحی اجرا می‌شوند. در ادامه، به توضیح برخی از روش‌های ریاضی تحلیل تنش می‌پردازیم.

معادلات دیفرانسیل

با استفاده از معادلات حرکت در اجسام پیوسته (برگرفته از قوانین نیوتن برای تبدیل گشتاور خطی و گشتاور زاویه‌ای)، قاعده تنش کوشی-اویلر و معادلات مشخصه مناسب می‌توان مسائل ابتدایی تحلیل تنش را به صورت فرمول درآورد.

با استفاده از این قوانین، یک دستگاه ﻣﻌﺎدﻻت دﯾﻔﺮاﻧﺴﯿﻞ ﺑﺎ ﻣﺸﺘﻘﺎت ﺟﺰﺋﯽ به دست می‌آید که رابطه بین میدان تانسور تنش نسبت به میدان تانسور کرنش در آن به صورت توابع مجهول آورده شده است. با حل معادلات بر اساس هر یک از میدان‌های تانسور تنش یا کرنش، می‌توان حاصلِ میدان دیگر را از طریق حل یک دستگاه معادلات به نام معادلات مشخصه به دست آورد. میدان‌های تانسور تنش و کرنش به طور معمول در هر یک از بخش‌های دستگاه به صورت پیوسته هستند. به همین دلیل می‌توان این بخش‌ها را به صورت محیط‌های پیوسته‌ای در نظر گرفت که معادلات مشخصه آن‌ها به طور جزئی تغییر می‌کنند.

در معادلات دیفرانسیل، نیروهای خارجی به صورت عبارت مستقل (عبارت سمت راست) و نیروهای متمرکز به صورت شرایط مرزی ظاهر می‌شوند. برای در نظر گرفتن نیروهای سطحی خارجی (مانند فشار یا اصطکاک محیط) می‌توان یک مقدار ثابت را به مؤلفه‌های آن سطح در تانسور تنش اعمال کرد. نیروهای خطی خارجی (مانند کشش) یا بارگذاری‌های نقطه‌ای (مانند وزن یک شخص ایستاده بر روی سقف) باعث ایجاد شرایط منحصر به فردی در میدان تنش می‌شوند. در این حالت می‌توان فرض کرد که این نیروها بر روی یک حجم یا سطح کوچک توزیع شده‌اند. از این‌رو، ابتدایی‌ترین مسئله در تحلیل تنش، یک «مسئله مقدار مرزی» (Boundary-Value Problem) است.

تحلیل تنش در محیط‌های الاستیک و خطی

در یک سیستم الاستیک، تغییر شکل ناشی از بارگذاری بر روی جسم پس از باربرداری به صورت کامل و خود به خود به حالت اول بازمی‌گردد. تنش‌های گسترش‌یافته درون یک محیط الاستیک، بر اساس «تئوری الاستیسیته» (Theory of Elasticity) و «تئوری کرنش بسیار کوچک» (Infinitesimal Strain Theory) محاسبه می‌شوند. هنگامی که اعمال بارگذاری منجر به تغییر شکل دائمی ماده شود، باید از معادلات مشخصه پیچیده‌تری استفاده کرد. این معادلات فرآیندهای فیزیکی دخیل در این نوع تغییر شکل (مانند جریان پلاستیک، ایجاد شکست، تغییر فاز و غیره) را در نظر می‌گیرند.

طراحی سازه‌های مهندسی معمولاً به گونه‌ای است که حداکثر تنش مورد انتظار، در محدوده الاستیک خطی (تعمیم قانون هوک برای محیط‌های پیوسته) قرار می‌گیرد. در این حالت، رابطه بین تغییر شکل‌های ناشی از تنش‌های داخلی و بارگذاری‌های اعمال شده به صورت خطی خواهد بود. درک معادلات خطی بسیار ساده‌تر از معادلات غیر خطی است؛ به دلیل اینکه راه حل آن‌ها (محاسبه تنش در هر نقطه دلخواه) به صورت یک تابع خطی از نیروهای اعمال شده خواهد بود. اگر بارگذاری‌ها به اندازه کافی کوچک باشند، می‌توان سیستم‌های غیر خطی را نیز به صورت خطی در نظر گرفت.

تنش درونی (پیش بارگذاری شده)

در یک «سازه پیش بارگذاری شده» (Preloaded Structure)، نیروها، تنش‌ها و کرنش‌های داخلی به وسیله روش‌های مختلف و پیش از اعمال نیروهای خارجی در درون سازه ایجاد می‌شوند. به عنوان مثال، کابل‌های سفت شده در یک سازه می‌توانند پیش از اعمال بارگذاری‌های خارجی، باعث ایجاد نیروهای داخلی شوند. یکی از مثال‌های متداول از سازه‌های پیش بارگذاری شده، شیشه حرارت دیده است. نیروها و تنش‌های کششی موجود در سطح داخلی و مرکز این نوع شیشه باعث ایجاد نیروهای فشاری و اعمال این نیروها به سطوح خارجی شیشه می‌شوند.

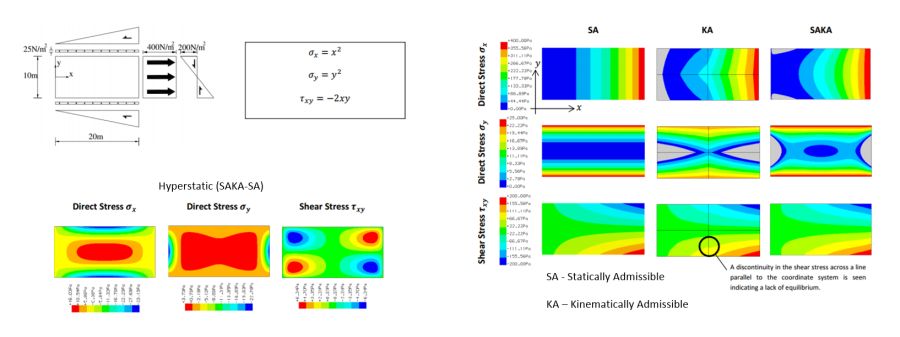
مسئله‌ای که در اینجا مطرح می‌شود، یک نوع «مسئله بدطرح» (Ill-Posed Problem) محسوب می‌شود زیرا دارای بی‌نهایت جواب است. در واقع، برای هر جسم جامد سه‌بعدی (حتی در وضعیت عدم وجود نیروهای خارجی) می‌توان بی‌نهایت میدان تانسور تنش غیر صفر در نظر گرفت که تمامی آن‌ها در حالت تعادل استاتیکی قرار دارند. این میدان‌ها اغلب با عنوان میدان‌های تنش هایپر استاتیک شناخته می‌شوند و با میدان‌های متعادل‌کننده نیروهای خارجی همراه هستند. حضور این میدان‌ها در تئوری الاستیسیته خطی، به منظور سازگاری با تنش/جابجایی و در تحلیل حدی، برای به حداکثر رساندن ظرفیت تحمل بار سازه یا اجزای آن ضروری است.

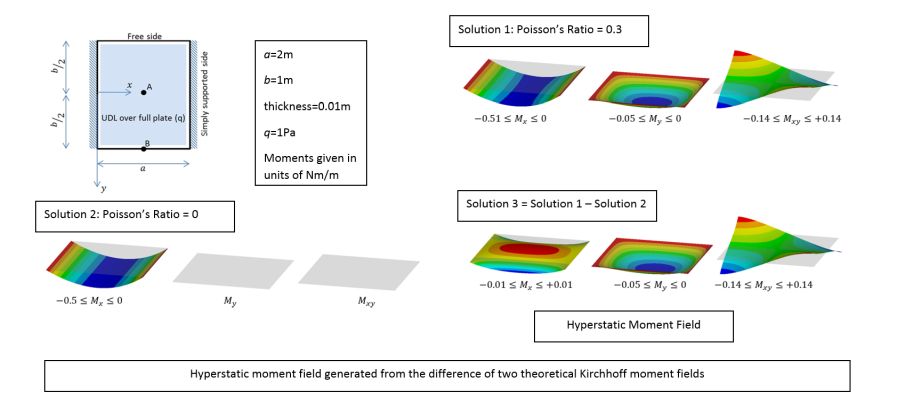
تنش‌های درونی در اثر عوامل فیزیکی متعددی به وجود می‌آیند. این عوامل را می‌توان به دو دسته زیر تقسیم‌بندی کرد:

• در حین فرآیند ساخت: «اکستروژن» (Extrusion)، «ریخته‌گری» (Casting) یا سخت‌شوندگی کرنش
• بعد از فرآیند ساخت: حرارت غیریکنواخت، تغییر در میزان رطوبت یا تغییر در ترکیب شیمیایی

اگر رفتار و واکنش سیستم در برابر بارگذاری به صورت خطی در نظر گرفته شود، حاصل جمع نتایج تحلیل یک سازه پیش بارگذاری شده با نتایج تحلیل همان سازه بدون پیش بارگذاری، تأثیر پیش بارگذاری را مشخص خواهد کرد.

در صورتی که امکان به کارگیری فرض خطی بودن مواد وجود نداشته باشد، هر گونه تنش درونی می‌تواند (به عنوان مثال با تغییر سختی مؤثر ماده) بر روی توزیع نیروهای داخلی ناشی از اعمال بارگذاری‌ها تأثیر بگذارد یا منجر به ایجاد یک شکست غیر منتظره در ماده شود. به همین دلیل، از روش‌های متعددی (مانند باز پخت کامل شیشه سرد کاری شده و قطعات فلزی، استفاده از لرزه‌گیر در ساختمان‌ها و اتصالات غلتکی در پل‌ها) به منظور اجتناب یا کاهش تنش‌های درونی استفاده می‌شود.

ساده‌سازی مسئله در تحلیل تنش

معمولاً اگر ابعاد فیزیکی و توزیع بارگذاری‌ها به گونه‌ای باشد که بتوان سازه را در یک یا دو بعد مورد ارزیابی قرار داد، از روش‌های ساده‌سازی تحلیل تنش استفاده می‌شود. به عنوان مثال در تحلیل یک پل، اگر تمام نیروها به صفحه مشترک قرارگیری خرپاها اعمال شوند، می‌توان این سازه سه‌بعدی به عنوان یک سازه مسطح در نظر گرفت. به علاوه، امکان در نظر گرفتن هر یک از اعضای خرپا به عنوان یک عضو تک‌بعدی تحت نیروهای محوری نیز وجود دارد. به این ترتیب، معادلات دیفرانسیل به یک دستگاه معادلات محدود با تعداد زیادی مجهول تبدیل می‌شوند.

اگر توزیع تنش در یک راستای مشخص به صورت یکنواخت، قابل پیش‌بینی یا بی‌اهمیت باشد، می‌توان از فرضیات کرنش و تنش صفحه‌ای استفاده کرد. در این شرایط، معادلات معرف میدان تنش به صورت تابعی خواهد بود که به جای سه مختصات دارای دو مختصات است.

به طور کلی، رابطه بین تانسورهای تنش و کرنش (حتی در صورت فرض رفتار الاستیک خطی)، توسط یک تانسور سختی با مرتبه چهار و 21 ضریب مستقل (یک ماتریس متقارن 6*6) تعریف می‌شود. استفاده از این تعریف پیچیده برای مواد ناهمسانگرد مورد نیاز است اما در بسیاری از مواد رایج، امکان ساده‌سازی آن وجود دارد. به عنوان مثال، در مواد ارتوتروپیک (Orthotropic) مانند چوب، سختی نسبت به هر یک از سه صفحه متعامد دارای تقارن است. از این‌رو، برای تعریف رابطه بین تنش و کرنش به دست آوردن 9 ضریب کفایت خواهد کرد. برای مواد همسانگرد، این تعداد به 2 ضریب کاهش پیدا می‌کند.

در برخی از بخش‌های دستگاه معادلات می‌توان نوع تنش (کشش یا فشار تک‌محوری، برش ساده، کشش یا فشار همسانگرد، پیچش، خمش و غیره) را به صورت پیش‌فرض تعیین کرد. در این بخش‌ها، میدان تنش با کم‌تر از شش مؤلفه یا حتی یک مؤلفه نیز قابل نمایش خواهد بود.

حل معادلات

در تمام مسائل مرتبط با تحلیل تنش، باید یک دستگاه معادلات دیفرانسیل ﺑﺎ ﻣﺸﺘﻘﺎت ﺟﺰﺋﯽ را به همراه شرایط مرزی مشخص برای محدوده‌های دوبعدی و سه‌بعدی حل کرد. اگر هندسه، روابط مشخصه و شرایط مرزی به اندازه کافی ساده باشند، می‌توان از روش‌های تحلیلی معادلات دیفرانسیل (فرم بسته) برای حل مسئله استفاده کرد. به منظور حل مسائل پیچیده‌تر، معمولاً از روش‌های عددی مانند روش المان محدود، تفاضل محدود و المان مرزی استفاده می‌شود.

ضریب ایمنی

هدف نهایی هر تحلیلی، مقایسه تنش، کرنش و تغییر شکل‌های ایجاد شده با مقادیر مجاز در طراحی است. به منظور جلوگیری از رخ دادن شکست، تمام سازه‌ها و اجزای آن‌ها باید با ظرفیتی بالاتر از بارهای مورد انتظار طراحی شوند. تنش مورد انتظار در هر عضو با مقاومت ماده مقایسه و نسبت این تنش به مقاومت محاسبه می‌شود. این نسبت همان «ضریب ایمنی» (Factor of Safety) یا اصطلاحاً «FOS» است.

در الزامات طراحی سازه باید نسبت تنش مجاز به تنش موجود (ضریب ایمنی یا ضریب طراحی) را بیشتر از 1 در نظر گرفت. ضریب طراحی (عددی بیشتر از 1)، عدم قطعیت مقادیر بارگذاری‌ها، مقاومت ماده و شکست‌های متعاقب را نشان می‌دهد. تنش، بار یا تغییر شکل مورد انتظار یک سازه با عنوان «تنش حدی» (Limit Stress)، «تنش طراحی» (Design Stress) یا «تنش اجرایی» (Working Stress) شناخته می‌شود. تنش حدی (حد تنش ماکسیمم)، کسری از مقاومت تسلیم ماده تشکیل‌دهنده سازه است. نسبت مقاومت نهایی به تنش مجاز، مقدار ضریب ایمنی در مقابل شکست نهایی را نشان می‌دهد.

با انجام چندین آزمایش بر روی نمونه‌های آزمایشگاهی می‌توان مقاومت نهایی و مقاومت تسلیم ماده را تعیین کرد. مقاومت ویژه ماده نیز از طریق تحلیل‌های آماری بر روی مقاومت به دست آمده از آزمایش بر روی چندین نمونه به دست می‌آید. تحلیل‌های آماری، امکان بهر گیری از یک روش منطقی برای تعیین مقاومت ماده با یک ریسک مشخص (به عنوان مثال، قطعیت 99.9 درصدی) را فراهم می‌کنند. با استفاده از این گونه روش‌ها، یک ضریب ایمنی جداگانه با مقداری بالاتر از ضریب ایمنی طراحی تعیین می‌شود.

هدف از تعیین ضریب ایمنی، جلوگیری از ایجاد تغییر شکل‌های مخرب در سازه و از بین رفتن کارایی آن است. به عنوان مثال، خم شدن دائمی بال یک هواپیما می‌تواند منجر به عدم استفاده مناسب از آن شود. با اینکه تسلیم مواد تشکیل‌دهنده یک سازه، کارایی آن را با مشکل مواجه می‌کند اما لزوماً باعث ایجاد شکست نمی‌شود. به این ترتیب، برای جلوگیری از شکست ناگهانی سازه (خسارات مالی و جانی)، ضریب ایمنی حاصل از مقاومت کششی نهایی مورد استفاده قرار می‌گیرد.

بال‌های هواپیما معمولاً با ضریب ایمنی 1.25 نسبت به مقاومت تسلیم بال و 1.5 نسبت به مقاومت نهایی آن طراحی می‌شوند. علاوه بر این، طراحی تجهیزات آزمایشگاهی مورد نیاز برای اعمال بار بر روی بال هواپیما با ضریب ایمنی نهایی 3 و سازه‌های دربرگیرنده این تجهیزات با ضریب ایمنی نهایی 10 صورت می‌گیرد. این مقادیر میزان اطمینان افراد مسئول به درک خود از محیط بارگذاری، قطعیت مقادیر به دست آمده برای مقاومت‌های مواد، دقت روش‌های تحلیلی مورد استفاده، ارزش سازه‌ها و اهمیت ایمنی افراد در حال پرواز، افراد حاضر در اطراف تجهیزات آزمایشگاهی و افراد حاضر در ساختمان‌ها را نشان می‌دهد.

با همه این تفاسیر، ضریب ایمنی در نهایت برای محاسبه حداکثر تنش مجاز به کار گرفته می‌شود:

$$\sigma _{{\mathrm {max}}}={\frac {{\text{UTS}}}{{\text{FOS}}}}$$

σ_max: تنش مجاز حداکثر؛ UTS: مقاومت کششی نهایی؛ FOS: ضریب ایمنی

انتقال بار در بین اجزای مختلف سازه

ارزیابی بارها و تنش‌های درون یک سازه رابطه مستقیمی با تعیین مسیرهای انتقال بارگذاری دارد. بارهای اعمال شده از طریق اتصالات فیزیکی بین قطعات مختلف و در داخل سازه‌ها جابجا می‌شوند. در سازه‌های ساده می‌توان انتقال بار را از طریق روش‌های مشاهده‌ای یا ریاضیات ساده تشخیص داد. برای سازه‌های پیچیده باید از روش‌های پیچیده‌تری مانند تئوری‌های مکانیک جامدات و روش‌های عددی استفاده کرد. از روش‌های عددی می‌توان به «روش سختی مستقیم» (Direct Stiffness Method) اشاره کرد که بیشتر با عنوان «روش المان محدود» (Finite Element Method) شناخته می‌شود.

به منظور تشخیص نقاط ضعف قطعات شکسته شده، از «مهندسی قانونی» (Forensic Engineering) یا «تحلیل شکست» (Failure Analysis) استفاده می‌شود. در این راستا، برای تشخیص دلیل یا دلایل شکستگی، قطعات مذکور مورد تحلیل قرار می‌گیرند. روش‌های مذکور به دنبال ضعیف‌ترین قطعه در مسیر بارگذاری می‌گردند. اگر ضعیف‌ترین قطعه همان قطعه شکسته شده باشد، می‌توان از طریق شواهد دلیل شکست را پیدا کرد. در غیر این صورت، باید به دنبال توضیح دیگری مانند وجود یک قطعه آسیب دیده با مقاومت کششی پایین‌تر بود.

تنش تک‌محوری

اساساً المان‌های خطی یک سازه را می‌توان به صورت یک‌بعدی در نظر گرفت. این المان‌ها اغلب تحت بارگذاری محوری قرار می‌گیرند. هنگام اعمال فشار یا کشش به یکی از المان‌های سازه، طول آن کاهش یا افزایش می‌یابد و مساحت سطح مقطع نیز با توجه به مقدار ضریب پواسون تغییر می‌کند. در مسائل مهندسی، تغییر شکل عضوهای سازه کوچک بوده و تغییرات مساحت سطح مقطع آن‌ها بسیار کم و قابل اغماض است. از این‌رو، مساحت هر عضو در هنگام تغییر شکل ثابت در نظر گرفته می‌شود. به تنش محاسبه شده در این حالت، «تنش مهندسی» (Engineering Stress) یا «تنش اسمی» (Nominal Stress) می‌گویند. مقدار این تنش با استفاده از مساحت اولیه سطح مقطع به دست می‌آید:

$$\sigma _{{\mathrm {e}}}={\tfrac {P}{A_{o}}}$$

P: بار اعمال شده؛ A₀: مساحت اولیه سطح مقطع

در موادی نظیر الاستومرها و پلاستیک‌ها، تغییرات مساحت سطح مقطع بسیار زیاد است.

در این حالت، برای تعیین میزان تنش واقعی، باید از مساحت واقعی سطح مقطع به جای مساحت اولیه استفاده کرد:

$$\sigma _{{\mathrm {true}}}=(1+\varepsilon _{{\mathrm e}})(\sigma _{{\mathrm e}})$$

σ_true: تنش واقعی؛ σ_e: تنش اسمی (مهندسی)؛ ε: کرنش اسمی (مهندسی)

رابطه بین کرنش واقعی و کرنش مهندسی به صورت زیر است:

$$\varepsilon _{{\mathrm {true}}}=\ln(1+\varepsilon _{{\mathrm e}})$$

ε_true: کرنش واقعی

در کشش تک‌محوری، تنش واقعی بزرگ‌تر از تنش اسمی و در فشار تک‌محوری، تنش اسمی بزرگ‌تر از تنش واقعی است.

نمایش گرافیکی حالت تنش

«دایره مور» (Mohr's Circle)، «بیضوی تنش لامه» (Lame's Stress Ellipsoid) و «کوادریک تنش کوشی» (Cauchy's Stress Quadric)، از روش‌های گرافیکی شناخته شده برای نمایش حالت تنش در یک نقطه هستند. این روش‌ها، امکان تعیین مقادیر تانسور تنش در یک نقطه مشخص از ماده را برای تمام صفحات گذرنده از آن نقطه فراهم می‌کنند. دایره مور، متداول روش گرافیکی تعیین حالت تنش است.

دایره مور

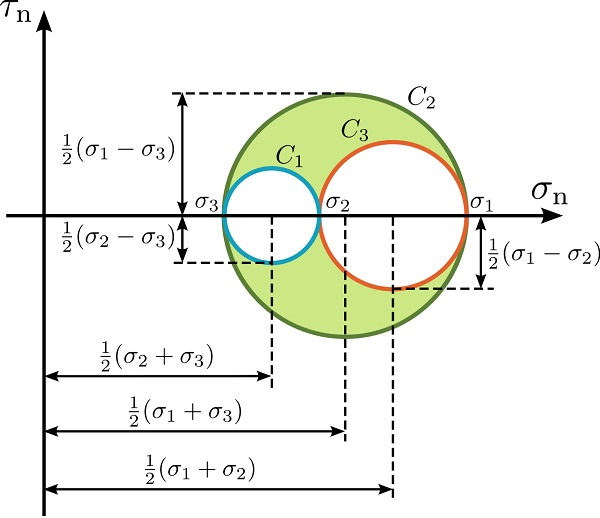
عنوان دایره مور، از روی نام «کریستین اتو مور» (Christian Otto Mohr)، یکی از مهندسان عمران آلمانی در قرن 19 میلادی گرفته شده است. این دایره، مکان هندسی نقاط معرف حالت تنش بر روی هر یک از صفحات ماده در تمام جهات را نشان می‌دهد.

طول و عرض دستگاه مختصات دایره مور، به ترتیب بیانگر مؤلفه‌های تنش نرمال (σ_n) و تنش برشی (τ_n) اعمال شده بر یک سطح مقطع بخصوص با بردار نرمال n و مؤلفه‌های (n₁,n₂,n₃) هستند.

بیضوی تنش لامه

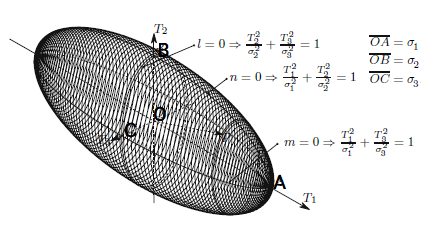
سطح بیضوی لامه، مکان هندسی نقاط انتهایی تمام بردارهای تنش بر روی تمام صفحات گذرنده از یک نقطه مشخص درون یک جسم پیوسته را نشان می‌دهد. به عبارت دیگر، تمام نقاط انتهایی بردارهای تنش در یک نقطه مشخص درون جسم پیوسته، بر روی سطح بیضوی تنش قرار گرفته‌اند. طول بردار شعاعی از مرکز بیضوی (بر روی نقطه مورد نظر) تا یک نقطه بر روی سطح بیضوی با طول بردار تنش در برخی از صفحات گذرنده از آن نقطه برابر است. برای نمایش حالت تنش در دو بعد، سطح مورد نظر به صورت یک بیضی نمایش داده می‌شود.

کوادریک تنش کوشی

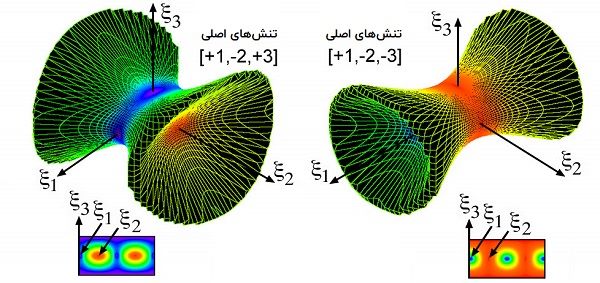
کوادریک تنش کوشی که با عنوان «سطح تنش» (Stress Surface) نیز شناخته می‌شود، سطحی مرتبه دو است. این سطح، تغییرات بردار تنش نرمال (σ_n) نسبت به تغییر جهت‌گیری صفحات گذرنده از یک نقطه مشخص را نشان می‌دهد.

تعیین حالت کامل تنش یک جسم در یک پیکربندی تغییر یافتهِ بخصوص و در یک زمانِ معین هنگام حرکت جسم، با دانستن 6 مؤلفه مستقل تانسور تنش (σ₁₁,σ₂₂,σ₃₃,σ₄₄,σ₅₅,σ₆₆) یا سه تنش اصلی (σ₁,σ₂,σ₃) در هر نقطه و در همان زمانِ معین امکان‌پذیر است. اگرچه، تحلیل‌های عددی و روش‌های تحلیلی فقط امکان محاسبه تانسور تنش در یک سری نقاط مجزا را فراهم می‌کنند. برای نمایش گرافیکی میدان تنش در دو بعد با استفاده از این روش، معمولاً از خطوط کنتوری زیر استفاده می‌شود:

• «خطوط هم‌فشار» (Isobars): منحنی‌هایی هستند که در امتداد آن‌ها، مقدار تنش اصلی (به عنوان مثال، σ₁) ثابت است.
• «خطوط هم‌رنگ» (Isochromatics): منحنی‌هایی هستند که در امتداد آن‌ها، مقدار تنش برشی ماکسیمم ثابت است. این منحنی‌ها مستقیماً از طریق روش‌های «نور کشسانی» (Photoelasticity) به دست می‌آیند.
• «خطوط هم ضخامت» (Isopachs): منحنی‌هایی هستند که در امتداد آن‌ها، مقدار تنش نرمال میانگین ثابت است.
• «خطوط ایزو استاتیک» (Isostatics) یا «مسیرهای تنش» (Stress Trajectories): مجموعه منحنی‌هایی که در هر نقطه به محورهای اصلی تنش مماس هستند (تصویر زیر).

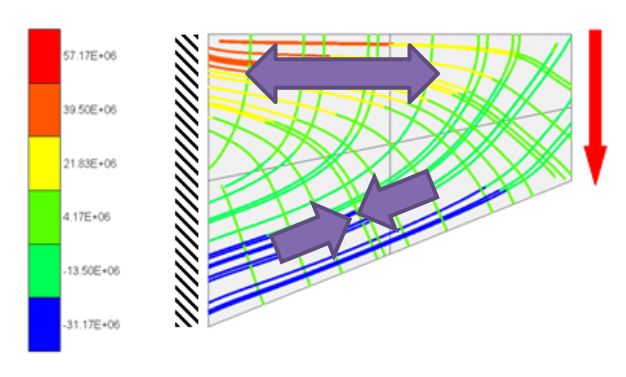
• «خطوط هم‌شیب» (Isoclinics): منحنی‌هایی هستند که بر روی آن‌ها، زاویه بین محورهای اصلی و یک جهت مرجع ثابت است.
• «خطوط لغزش» (Slip Lines): منحنی‌هایی هستند که تنش برشی بر روی آن‌ها دارای مقدار ماکسیمم است.

امیدواریم این مقاله برایتان مفید واقع شده باشد. اگر به یادگیری موضوعات مشابه علاقه‌مند هستید، مطالب زیر را به شما پیشنهاد می‌کنیم:

• مجموعه آموزش های مهندسی عمران
• مجموعه آموزش‌های دروس مهندسی مکانیک
• آموزش مقاومت مصالح
• مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خواص مکانیکی مواد

^^