انرژی کرنشی در میله های تحت پیچش – به زبان ساده

در مبحث «انرژی کرنشی در مواد الاستیک خطی»، به معرفی کامل مفاهیم اولیه انرژی کرنشی پرداختیم و دریافتیم که اعمال بار بر روی سازه‌ها باعث انجام کار و ایجاد انرژی کرنشی در آن‌ها می‌شود. در این مقاله، به بررسی مفاهیم اولیه مورد نیاز برای تعیین انرژی کرنشی در میله‌های تحت پیچش (یکنواخت و غیر یکنواخت) خواهیم پرداخت. در انتها نیز به منظور آشنایی با نحوه به کارگیری روابط ارائه شده، چند مثال را تشریح خواهیم کرد.

پیچش یکنواخت

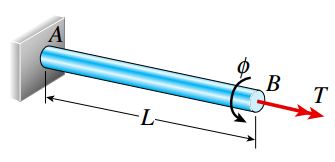
میله منشوری زیر را در نظر بگیرید. به دلیل اعمال گشتاور پیچشی T، میله AB در معرض پیچش خالص قرار گرفته است. با اعمال بارهای استاتیک، انتهای آزاد میله تحت زاویه φ دوران می‌کند.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

اگر ماده تشکیل‌دهنده میله الاستیک خطی باشد و از قانون هوک پیروی کند، رابطه بین گشتاور اعمال شده و زاویه پیچش نیز خطی خواهد بود.

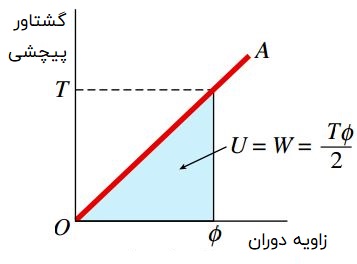
شکل زیر، رابطه بین گشتاور پیچشی و زاویه پیچش برای یک میله تحت پیچش خالص را نمایش می‌دهد. کار انجام شده توسط گشتاور پیچشی (در حین چرخش تحت زاویه φ) با مساحت زیر خط OA در منحنی گشتاور-دوران (ناحیه رنگی) برابری می‌کند.

بر اساس اصل پایستگی انرژی، اگر هیچ انرژی از طریق حرارت جذب یا دفع نشود، انرژی کرنشی میله با کار انجام شده توسط بارگذاری برابر خواهد بود. با در نظر گرفتن این اصل، رابطه زیر برای تعیین انرژی کرنشی میله (U) به دست می‌آید:

رابطه بالا، معادلِ رابطه U=W=Pδ/2 در میله تحت بارگذاری محوری است. با استفاده از رابطه φ=TL/GI_p می‌توان انرژی کرنشی را به صورت زیر نوشت:

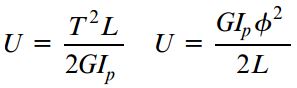
رابطه سمت چپ، انرژی کرنشی را بر حسب بار اعمال شده و رابطه سمت راست، این انرژی را بر حسب زاویه پیچش بیان می‌کند. واحد کار و انرژی کرنشی در سیستم SI، ژول (J) یا نیوتن متر (N.m) است. این دو کمیت در سیستم یکاهای آمریکایی اغلب با واحد فوت-پوند (ft-lb) و گاهی اوقات نیز با واحدهای اینچ-پوند (in-lb) و اینچ-کیلوپوند (in-k) بیان می‌شود.

پیچش غیریکنواخت

اگر میله‌ای در معرض پیچش غیر یکنواخت قرار داشته باشد، برای تعیین انرژی کرنشی درون آن باید از روابط اضافی استفاده کرد.

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

در مواردی که میله از چند بخش منشوری با گشتاورهای پیچشی ثابت تشکیل شده است، انرژی کرنشی کل از جمع انرژی کرنشی هر بخش به دست می‌آید:

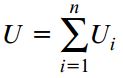
U_i: انرژی کرنشی بخش i ام؛ i: شماره هر بخش؛ n: تعداد بخش‌ها

برای تعیین انرژی‌های کرنشی، رابطه بالا به فرم زیر درمی‌آید:

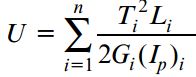
T_i: گشتاور پیچشی بخش i ام؛ L_i: طول بخش i ام؛ G_i: مدول برشی بخش i ام؛ I_p)_i): ممان اینرسی قطبی بخش i ام

اگر سطح مقطع میله یا گشتاور پیچشی درون آن در امتداد محور طولی تغییر کند، برای تعیین انرژی کرنشی کل باید انرژی کرنشی هر المان را مشخص کرد و سپس از طول میله انتگرال گرفت.

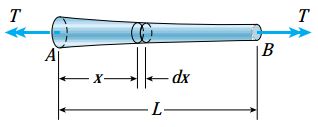
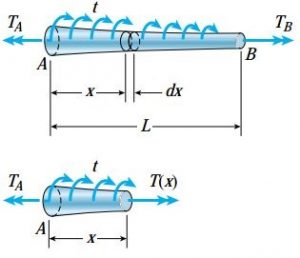
برای المانی با طول dx، انرژی کرنشی به صورت زیر محاسبه می‌شود:

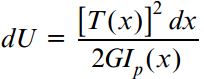
(T(x: گشتاور پیچشی اعمال شده بر روی المان مورد نظر؛ (I_p(x: ممان اینرسی قطبی سطح مقطع المان

به این ترتیب، انرژی کرنشی درون کل میله برابر است با:

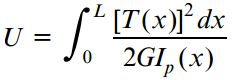
روابط بالا با روابط ارائه شده برای میله‌های تحت بار محوری شباهت زیادی دارند. نحوه به کارگیری این روابط برای تعیین مؤلفه‌های پیچش غیریکنواخت در مثال‌های آخر مقاله تشریح شده است.

توجه: در هنگام محاسبه انرژی کرنشی با استفاده از روابط ارائه شده در این بخش باید به خاطر داشته باشید که این روابط تنها برای میله‌های الاستیک خطی با زوایای پیچش کوچک قابل استفاده هستند. علاوه بر این، انرژی کرنشی سازه‌ای که در معرض چندین بار قرار دارد با جمع انرژی‌های کرنشی ناشی از هر بار برابر نخواهد بود. این نکته در یکی از مثال‌های مبحث «انرژی کرنشی در مواد الاستیک خطی» به خوبی قابل مشاهده است.

چگالی انرژی کرنشی در شرایط بارگذاری پیچشی

در شرایط بارگذاری پیچشی، هر یک از المان‌های میله تحت برش خالص قرار دارند. از این‌رو، به دست آوردن رابطه‌ای برای تعیین انرژی کرنشی بر حسب تنش‌های برشی، روش مناسبی برای تحلیل این شرایط خواهد بود.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

به این منظور، المان نمایش داده شده در شکل زیر را مورد بررسی قرار می‌دهیم. تمام صفحات کناری این المان در معرض تنش‌های برشی قرار دارند. برای سادگی تحلیل، صفحه جلویی المان را به شکل مربعی با طول h در نظر می‌گیریم. شکل زیر، نمای دوبعدی المان تنش را نمایش می‌دهد. توجه داشته باشید که این المان دارای ضخامت t در راستای عمود بر صفحه است.

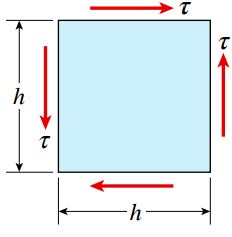
با اعمال تنش‌های برشی و ایجاد اعوجاج در المان مورد نظر، صفحه جلویی آن به شکل لوزی درمی‌آید. میزان تغییر زاویه هر گوشه المان با کرنش برشی γ برابر است.

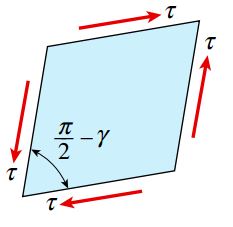
شکل زیر، نیروهای برشی اعمال شده بر روی صفحات کناری المان مورد بررسی را نمایش می‌دهد. با ضرب تنش‌های برشی در مساحت هر صفحه (ht)، میزان نیروهای برشی نیز به دست می‌آید:

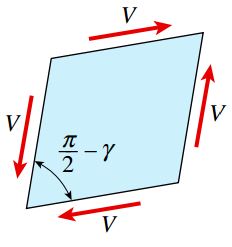
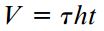
با تغییر شکل المان، نیروهای V باعث ایجاد کار می‌شوند. به منظور محاسبه کارِ انجام شده باید فاصله نسبی حرکت نیروها را تعیین کنیم. اگر المان تحت نیرو را به گونه‌ای بچرخانیم که دو صفحه آن مطابق شکل زیر به صورت افقی درآیند، محاسبه کارِ انجام شده راحت‌تر خواهد بود.

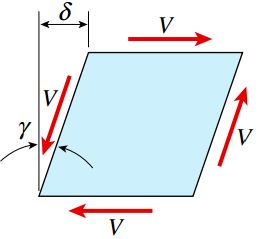
با توجه به شکل بالا، صفحه بالایی المان نسبت به صفحه پایینی آن به اندازه δ جابجا شده است. مقدار این جابجایی از ضرب کرنش برشی در طول المان به دست می‌آید:

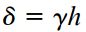
با فرض الاستیک خطی بودن ماده و پیروی آن از قانون هوک، کار انجام شده و انرژی کرنشی ذخیره شده در المان مورد بررسی برابر با رابطه زیر خواهد بود:

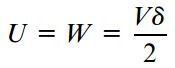
توجه داشته باشید که نیروهای موجود بر روی صفحات سمت راست و چپ المان در راستای اعمال خود جابجا نمی‌شوند. به همین دلیل، کار انجام شده توسط آن‌ها صفر است. با جایگذاری V=τht و δ=γh در رابطه بالا، خواهیم داشت:

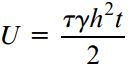
حجم المان از رابطه h²t به دست می‌آید. به این ترتیب، چگالی انرژی کرنشی (انرژی کرنشی بر واحد حجم) برابر است با:

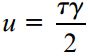
با توجه به قانون هوک برای مواد تحت برش، رابطه چگالی انرژی کرنشی در شرایط بر خالص به صورت زیر خواهد بود:

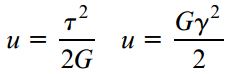
چگالی انرژی کرنشی در سیستم SI با واحد ژول بر متر مکعب (J/m³) و در سیستم یکاهای آمریکایی با واحد اینچ-پوند (in-lb) یا دیگر واحدهای مشابه بیان می‌شود. این واحدها با واحدهای تنش یکسان هستند. از این‌رو می‌توان چگالی انرژی کرنشی را با واحدهای پاسکال (Pa) یا پوند بر اینچ مربع (psi) نیز بیان کرد. این کمیت به منظور تعیین زاویه پیچش لوله‌های جدار نازک مورد استفاده قرار می‌گیرد.

مثال‌ها

برای آشنایی با نحوه به کارگیری روابط ارائه شده در مسائل مربوط به تعیین انرژی کرنشی حاصل از پیچش و برش خالص، به تشریح چند مثال می‌پردازیم.

فیلم آموزش مقاومت مصالح در فرادرس

کلیک کنید

مثال 1

شکل زیر، یک میله دایره‌ای توپر با طول L را نمایش می‌دهد. یک انتهای میله AB به صورت ثابت و دیگری آزاد است. در شکل‌های الف تا ج، میله AB تحت سه حالت بارگذاری متفاوت قرار دارد. در حالت اول، گشتاور پیچشی T_a بر روی انتهای آزاد میله، در حالت دوم، گشتاورهای پیچشی T_b بر روی نقطه میانی میله و در حالت سوم، گشتاورهای T_a و T_b به طور هم‌زمان اعمال می‌شوند. با در نظر گرفتن گشتاور اول T_a=100N.m، گشتاور دوم T_b=150N.m، طول میله L=1.6m، مدول برشی G=80GPa و ممان اینرسی قطبی Ip=79.52x10³mm⁴، رابطه مورد نیاز برای تعیین انرژی کرنشی ذخیره شده و مقدار این انرژی در حالت‌های مختلف را به دست آورید؟

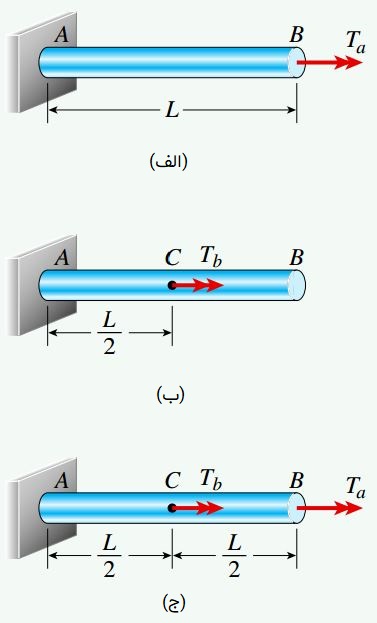
الف) رابطه گشتاور پیچشی اعمال شده بر روی انتهای آزاد میله

برای این حالت، انرژی کرنشی با استفاده از رابطه زیر به دست می‌آید:

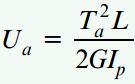
ب) رابطه گشتاور پیچشی اعمال شده بر نقطه میانی میله

در صورت اعمال گشتاور پیچشی بر نقطه میانی، از رابطه زیر برای تعیین انرژی کرنشی در بخش AC استفاده می‌شود:

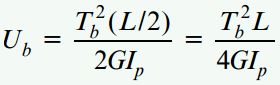
ج) رابطه اعمال هم‌زمان گشتاورهای پیچشی بر روی انتهای آزاد و نقطه میانی میله

هنگام اعمال دو بار متفاوت بر روی میله، T_a به عنوان گشتاور بخش CB و حاصلِ T_a+T_b به عنوان گشتاور بخش AC در نظر گرفته می‌شود. به این ترتیب، انرژی کرنشی کل میله برابر است با:

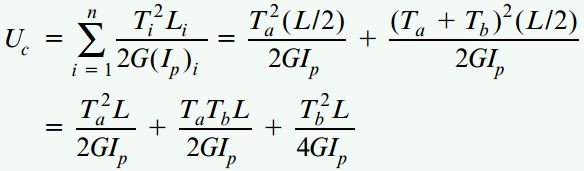
توجه: با مقایسه روابط معرفی شده در بخش‌های الف تا ج می‌توان مشاهده کرد که انرژی کرنشی حاصل از اعمال هم‌زمان دو بار متفاوت برابر با حاصل جمع انرژی‌های کرنشی حاصل از هر بار نخواهد بود؛ چراکه انرژی کرنشی یک تابع مرتبه دوم از بارهای اعمال شده به حساب می‌آید و رابطه بین این دو کمیت خطی نیست.

محاسبات عددی

با جایگذاری اطلاعات مسئله در روابط بالا، مقادیر عددی انرژی‌های کرنشی به دست می‌آیند:

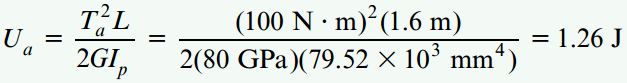
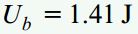
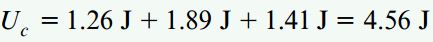
توجه داشته باشید که عبارت میانی رابطه آخر از حاصل‌ضرب گشتاورهای اعمال شده به دست می‌آید و تأثیر بسزایی بر روی مقدار نهایی انرژی کرنشی دارد.

مثال 2

میله منشوری AB با یک انتهای ثابت و یک انتهای آزاد در معرض گشتاوری با شدت یکنواخت t بر واحد فاصله قرار گرفته است. با توجه به کمیت‌های نمایش داده شده در شکل زیر، موارد الف و ب را تعیین کنید:

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

• الف) رابطه انرژی کرنشی میله
• ب) انرژی کرنشی شفت توخالی مورد استفاده برای حفر زمین (با در نظر گرفتن اطلاعات زیر)

t=480lb-in/in, L=12ft, G=11.5x10⁶psi, Ip=17.18in⁴

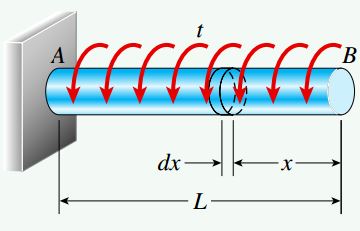
الف) انرژی کرنشی میله

اولین قدم برای حل مسئله، تعیین گشتاور (T(x در فاصله x از انتهای آزاد میله است. این گشتاور پیچشی با مجموع گشتاورهای اعمال شده بر روی بخشی از میله برابری می‌کند که در فاصله x=0 تا x=x قرار دارد. گشتاور داخلی موجود در این بخش، از ضرب شدت گشتاور پیچشی در طول x به دست می‌آید:

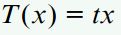
با جایگذاری رابطه بالا در رابطه ارائه شده برای پیچش غیریکنواخت، خواهیم داشت:

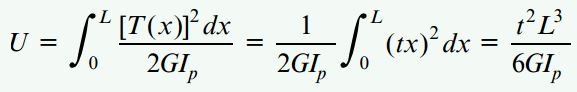
این رابطه، انرژی کرنشی ذخیره شده در کل میله را تعیین می‌کند.

ب) محاسبات عددی

به منظور تعیین انرژی کرنشی شفت توخالی، اطلاعات بخش ب مسئله را درون رابطه به دست آمده در بخش الف قرار می‌دهیم:

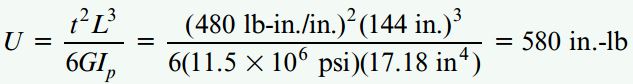
توجه: این مثال، نحوه استفاده از انتگرال‌گیری برای تعیین انرژی کرنشی درون میله‌ای که تحت گشتاور پیچشی توزیع شده قرار دارد را نمایش می‌دهد.

مثال 3

شکل زیر، یک میله مخروطی توپر با مقطع دایره‌ای را نمایش می‌دهد. انتهای سمت راست میله AB ثابت است و انتهای سمت چپ آن در معرض گشتاور پیچشی T قرار دارد. قطر میله به صورت خطی از dA تا dB تغییر می‌کند. با توجه به اطلاعات مسئله و پیکربندی میله، زاویه پیچش در انتهای A را با استفاده از رابطه بین انرژی کرنشی و کار انجام شده توسط گشتاور T به دست آورید.

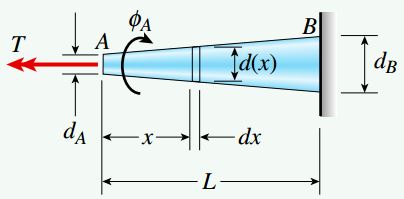
با توجه به قانون پایستگی انرژی، کار انجام شده توسط گشتاور پیچشی با انرژی کرنشی موجود در میله برابر است (U=W). کار انجام شده از طریق رابطه زیر تعیین می‌شود:

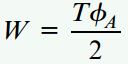
رابطه انرژی کرنشی نیز به صورت زیر است:

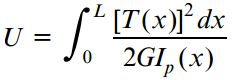
برای استفاده از رابطه بالا، در ابتدا باید عبارت‌های مربوط به گشتاور پیچشی (T(x و ممان اینرسی قطبی (I_p(x را پیدا کنیم. گشتاور پیچشی در امتداد محور میله ثابت و برابر با بار T است. ممان اینرسی قطبی نیز از رابطه زیر به دست می‌آید:

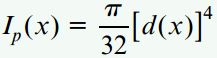
(d(x، قطر میله در فاصله x از انتهای A را نمایش می‌دهد. با توجه به هندسه میله داریم:

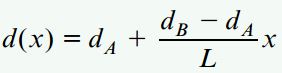
به این ترتیب:

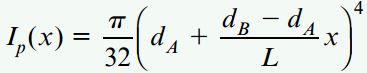
با جایگذاری این معادله در رابطه انرژی کرنشی خواهیم داشت:

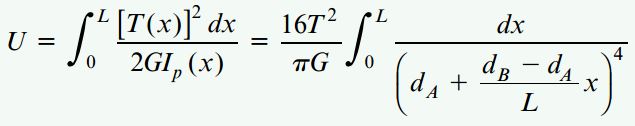
جواب انتگرال عبارت بالا برابر است با:

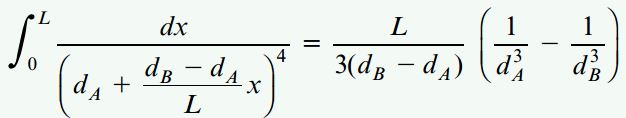
از این‌رو، رابطه انرژی کرنشی میله مخروطی مورد تحلیل به صورت زیر خواهد بود:

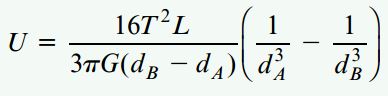
اگر معادله بالا را با معادله کار برابر قرار دهیم و رابطه به دست آمده را بر حسب φ_A حل کنیم، به معادله زیر می‌رسیم:

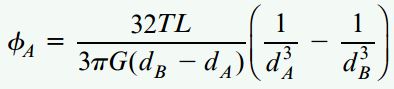
این معادله، مقدار زاویه پیچش در نقطه A را محاسبه می‌کند. روش ارائه شه در این مثال تنها برای میله‌ای قابل استفاده است که تحت یک بار منفرد قرار دارد. برای آشنایی با حالت‌های دیگر می‌توانید به مباحث «تحلیل میله‌های تحت پیچش» و «پیچش غیر یکنواخت» مراجعه کنید.

^^