پیچش غیر یکنواخت (Nonuniform Torsion) و حالت های مختلف آن – با مثال های کاربردی

در مباحث «پیچش»، «تغییر شکل‌های ناشی از پیچش» و «تحلیل میله‌های تحت بارگذاری پیچشی» به معرفی مفهوم پیچش و روابط مورد نیاز برای تحلیل عضوهای سازه‌ای در شرایط بارگذاری پیچشی پرداختیم. بر اساس مفاهیم ارائه شده در این مطالب، پیچش خالص زمانی رخ می‌دهد که تنها یک انتهای میله منشوری تحت گشتاورهای پیچشی یکنواخت قرار داشته باشد. در این مقاله، به معرفی پیچش غیر یکنواخت و روابط مربوط به آن خواهیم پرداخت. این حالت بارگذاری با پیچش خالص متفاوت است. در پیچش غیر یکنواخت، نیازی به منشوری بودن میله نیست. علاوه بر این، گشتاورهای پیچشی می‌توانند بر روی هر نقطه‌ای از میله اعمال شوند. روش‌های مختلفی برای تحلیل این شرایط وجود دارند. به منظور آشنایی با این روش‌ها، سه حالت مختلف از این نوع بارگذاری را معرفی خواهیم کرد. در انتها نیز برای آشنایی با نحوه به کارگیری روابط معرفی‌شده در هر حالت، چند مثال کاربردی را تشریح خواهیم کرد.

حالت اول پیچش غیر یکنواخت

در این حالت، میله مورد تحلیل همانند شکل زیر از چندین بخش منشوری تشکیل می‌شود و هر یک از این بخش‌ها تحت گشتاورهای پیچشی ثابت قرار می‌گیرد. شکل زیر، یک میله دوبخشی با قطرهای متفاوت را نمایش می‌دهد. گشتاورهای T₃ ،T₂ ،T₁ و T₄ به ترتیب بر روی نقاط C ،B ،A و D اعمال می‌شوند.

برای تحلیل این حالت، باید میله را به گونه‌ای تقسیم کنیم که هر بخش آن دارای سطح مقطع یکنواخت (منشوری) بوده و تحت یک گشتاور پیچشی ثابت قرار داشته باشد. به این ترتیب، میله مورد تحلیل ما در این مثال دارای سه بخش BC ،AB و CD خواهد بود. هر یک از بخش‌ها تحت پیچش خالص قرار دارند. در نتیجه، روابط ارائه شده در مبحث «تغییر شکل‌های ناشی از پیچش» برای این بخش‌ها نیز قابل استفاده هستند.

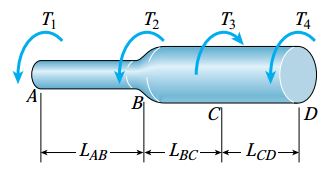
اولین گام برای تحلیل، تعیین مقدار و جهت‌گیری گشتاور داخلی در هر بخش است. مقادیر گشتاورها معمولاً از طریق بررسی و مشاهدات آزمایشگاهی مشخص می‌شوند. اگرچه، با ایجاد مقاطع عرضی، رسم نمودارهای جسم آزاد و حل معادلات تعادل نیز می‌توان کمیت‌های مورد نیاز را محاسبه کرد. به عنوان مثال، میله بالا را در نظر بگیرید. فرآیند تحلیل این میله در شکل زیر نمایش داده شده است.

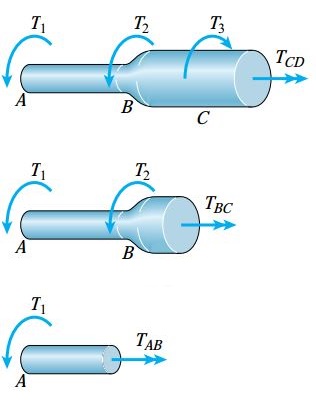
در مقطع اول، بخش CD را از میله جدا می‌کنیم و به جای آن، گشتاور داخلی T_CD را قرار می‌دهیم. این کار را تا رسیدن به بخش AB ادامه می‌دهیم. با توجه به نمودار جسم آزاد، کمیت‌های T_BC ،T_AB و T_CD به صورت زیر به دست می‌آیند:

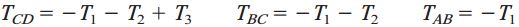
مقدار هر یک از این گشتاورها در طولِ بخشِ مربوط به خود ثابت است. برای به دست آوردن تنش‌های برشی در هر بخش، تنها به مقادیر این گشتاورها نیاز داریم. به منظور تعیین زاویه پیچش برای کل میله و جمع صحیح این زوایا نیز باید از جهت پیچش هر بخش اطلاع داشته باشیم. به این ترتیب از یک قاعده علامت‌گذاری مشخص برای گشتاورهای داخلی استفاده می‌کنیم.

در صورتی که بردار گشتاور داخلی از سطح مقطع میله خارج شود، علامت آن مثبت و اگر به سطح مقطع وارد شود، علامت آن منفی خواهد بود. به این ترتیب، تمام گشتاورهای داخلی نمایش داده شده در شکل زیر، مثبت هستند. در صورتی که علامت یک گشتاور پس از انجام محاسبات مثبت باشد، جهت اعمال آن با جهت فرضی یکسان خواهد بود. در غیر این صورت، جهت اعمال گشتاور مخالف جهت فرضی است.

تنش برشی ماکسیمم در هر بخش توسط رابطه پیچش (τ_max=Tr/I_P) به سادگی تعیین می‌شود. به عنوان مثال، مقدار تنش برشی ماکسیمم در بخش BC با استفاده از قطر این بخش و گشتاور پیچشی T_BC=-T₁-T₂ به دست می‌آید. تنش ماکسیمم در کل میله، بزرگ‌تر از تمام تنش‌های محاسبه شده در سه بخش دیگر خواهد بود. زاویه پیچش هر بخش نیز از طریق رابطه φ=TL/GI_P مورد محاسبه قرار می‌گیرد. زاویه پیچش کل برای یک انتهای میله نسبت به انتهای دیگر آن نیز با جمع جبری زوایای پیچش هر بخش تعیین می‌شود:

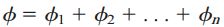
φ₁: زاویه پیچش بخش اول؛ φ₂: زاویه پیچش بخش دوم؛ n: تعداد بخش‌ها

با توجه به رابطه زاویه پیچش، فرمول کلی زیر برای محاسبه زاویه پیچش کل به دست می‌آید:

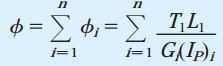
i: اندیس شمارنده بخش‌های مختلف؛ T_i: گشتاور داخلی در بخش i ام؛ Li: طول بخش i ام؛ G_i: مدول برشی بخش i ام؛ I_P)_i): ممان اینرسی قطبی بخش i ام (برای مقاطع دایره‌ای این کمیت برابر πd⁴/32)

گشتاورها و زوایای پیچش می‌توانند مثبت یا منفی باشند. به همین دلیل، برای تعیین زاویه پیچش کل φ از جمع جبری زاویه پیچش تمام بخش‌ها استفاده می‌کنیم. این فرآیند در مثال‌های انتهای مقاله به خوبی نمایش داده شده است.

حالت دوم پیچش غیر یکنواخت

در این حالت، سطح مقطع میله به طور پیوسته تغییر می‌کند و میله تحت گشتاور پیچشی ثابت قرار می‌گیرد (شکل زیر). در صوت ثابت بودن گشتاور پیچشی، تنش برشی ماکسیمم در یک میله توپر، همیشه بر روی سطح مقطعی ایجاد می‌شود که دارای کوچک‌ترین قطر است.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

این موضوع معمولاً برای لوله‌ها نیز صدق می‌کند. در این موارد، به منظور محاسبه تنش برشی ماکسیمم فقط باید کوچک‌ترین سطح مقطع میله یا لوله را مورد ارزیابی قرار داد. در موارد دیگر، مقدار ماکسیمم تنش برشی با بررسی نقاط مختلف و مقایسه تنش‌های موجود بر روی آن‌ها به دست می‌آید.

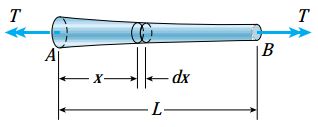
به منظور تعیین زاویه پیچش، المان dx در فاصله x از انتهای میله را در نظر می‌گیریم. زاویه چرخش برای این المان با استفاده از رابطه زیر تعیین می‌شود:

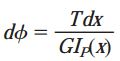
(I_P(x: ممان اینرسی قطبی سطح مقطعی در فاصله x از انتهای میله

به این ترتیب، زاویه پیچش برای کل میله با جمع زوایای پیچش تمام المان‌ها به دست می‌آید:

اگر عبارت مربوط به (I_P(x پیچیده نباشد، امکان حل تحلیلی انتگرال بالا فراهم خواهد شد (مانند مثال 2 در انتهای مقاله). در غیر این صورت، انتگرال را باید به صورت عددی مورد محاسبه قرار داد.

حالت سوم پیچش غیر یکنواخت

در این حالت، سطح مقطع میله به طور پیوسته تغییر می‌کند و میله تحت گشتاور پیچشی متغیر قرار می‌گیرد. بخش بالایی شکل زیر، اعمال یک گشتاور پیچشی توزیع شده بر روی یک میله مخروطی را نمایش می‌دهد.

شدت این گشتاور پیچشی، t بر واحد فاصله است. گشتاور داخلی (T(x به طور پیوسته در راستای محور میله تغییر می‌کند. مقدار این گشتاور با کمک نمودار جسم آزاد (بخش پایینی شکل) و معادله تعادل به دست می‌آید. ممان اینرسی قطبی (I_P(x نیز همانند حالت دوم تعیین می‌شود.

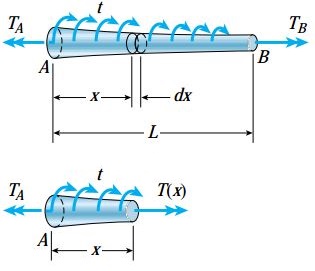
با مشخص کردن روابط گشتاور و ممان اینرسی قطبی به صورت تابعی از x، می‌توان از رابطه پیچش برای تعیین نحوه تغییر تنش برشی در راستای محور طولی میله استفاده کرد. به این ترتیب، صفحه دربرگیرنده تنش برشی ماکسیمم و سپس مقدار این تنش قابل محاسبه خواهد بود. زاویه پیچش در این حالت همانند حالت دوم تعیین می‌شود؛ با این تفاوت که علاوه بر ممان اینرسی قطبی، میزان گشتاور پیچشی نیز در امتداد محور میله تغییر می‌کند. در نتیجه، رابطه زیر برای تعیین زاویه پیچش به دست می‌آید:

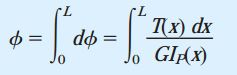
این انتگرال در برخی از موارد به صورت تحلیلی و در موارد دیگر به صورت عددی قابل حل است.

نکات تکمیلی

مطالب و روابط ارائه شده در این مقاله، برای میله‌های الاستیک خطی با مقاطع دایره‌ای شکل (توپر یا توخالی) کاربرد دارند. به علاوه، تنش‌های به دست آمده از طریق رابطه پیچش نیز برای مقاطع دور از نواحی تمرکز تنش معتبر هستند. با این وجود، نواحی تمرکز تنش بر روی مقدار زاویه پیچش و روابط معرفی شده برای آن تأثیر کمی دارند. به خاطر داشته باشید که روابط پیچش و زاویه پیچش برای میله‌های منشوری (سطح مقطع یکنواخت) ارائه شده‌اند.

فیلم آموزش مقاومت مصالح ۲ + مفاهیم کلیدی در فرادرس

کلیک کنید

اگرچه، در صورت وجود تغییرات کوچک و تدریجی در قطر میله می‌توان این روابط را برای مقاطع غیر یکنواخت نیز مورد استفاده قرار داد. بر اساس یک قانون سرانگشتی، اگر زاویه بین دو انتهای یک میله مخروطی کمتر از 10 درجه باشد، روابط مربوط به میله‌های منشوری برای میله‌های مخروطی نیز قابل استفاده خواهند بود.

توجه: حالت‌های مختلف پیچش غیریکنواخت محدود به سه مورد معرفی شده در این مقاله نیستند. حالت‌های دیگر را نیز می‌توان با استفاده از فرآیندهای مشابه مورد تحلیل قرار داد.

مثال‌های کاربردی

در ادامه به منظور آشنایی بیشتر با پیچش غیر یکنواخت و نحوه تحلیل حالت‌های مختلف آن، به تشریح دو مثال کاربردی می‌پردازیم.

مثال 1

شکل زیر، یک شفت توپر با قطر 30 میلی‌متر را نمایش می‌دهد. این شفت بین دو یاتاقان A و B قرار دارد و می‌تواند آزادانه درون این یاتاقان‌های دوران کند. شفت ABCDE توسط چرخ‌دنده C کنترل می‌شود. این چرخ‌دنده، گشتاور پیچشی T₂=420N.m را در جهت نمایش داده شده به شفت وارد می‌کند. چرخ‌دنده‌های B و D که تحت کنترل شفت قرار دارند، با گشتاورهای T₁=275N.m و T₂=175N.m در خلاف جهت T₂ اعمال می‌شوند و در مقابل آن مقاومت می‌کنند. طول بخش‌های BC و CD به ترتیب برابر با L_BC=500mm و L_CD=400mm و مدول برشی آن‌ها برابر با G=80GPa است. با توجه به اطلاعات مسئله، تنش برشی ماکسیمم در هر یک از بخش‌های شفت و زاویه پیچش بین چرخ‌دنده‌های B و D را محاسبه کنید.

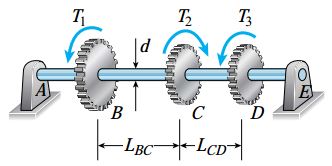
راه حل

هر یک از بخش‌های میله به صورت منشوری هستند و تحت پیچش‌های ثابت قرار گرفته‌اند (حالت اول پیچش غیر یکنواخت). به این ترتیب، گام اول در تحلیل این مسئله، تعیین گشتاورهای اعمال شده بر روی هر بخش خواهد بود. بعد از این کار، امکان محاسبه تنش‌های برشی نیز فراهم می‌شود.

گشتاورهای اعمال شده بر روی هر بخش میله

به دلیل صرف نظر کردن از وجود اصطکاک در تکیه‌گاه‌ها (یاتاقان‌ها)، مقدار گشتاورهای موجود در بخش‌های انتهایی (AB و DE) صفر خواهد بود. از این‌رو، هیچ تنش و هیچ زاویه پیچشی در این بخش‌ها وجود نخواهد داشت. گشتاور موجود در بخش CD، از طریق حذف این بخش و رسم نمودار جسم آزاد بخش‌های باقیمانده به دست می‌آید. برای انجام محاسبات، جهت گشتاور پیچشی T_CD را مثبت فرض می‌کنیم (بردار آن از سطح مقطع دور می‌شود). در ست یا غلط بودن این فرض در ادامه مشخص خواهد شد.

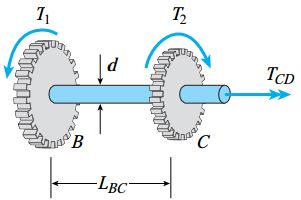
با توجه به تعادل جسم آزاد:

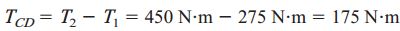
علامت مثبت T_CD نشان می‌دهد که فرض ما در مورد جهت‌گیری گشتاور پیچشی بخش CD درست بوده است. گشتاور موجود در بخش BC را نیز به همین صورت تعیین می‌کنیم. به این منظور، با حذف این بخش و رسم نمودار جسم آزاد بخش‌های باقیمانده، خواهیم داشت:

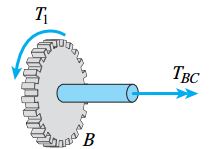
توجه داشته باشید که این گشتاور پیچشی دارای علامت منفی است. در نتیجه، جهت‌گیری آن، مخالف جهت‌گیری نمایش داده شده در شکل بالا خواهد بود.

تنش‌های برشی

تنش‌های برشی ماکسیمم در بخش‌های BC و CD از طریق رابطه پیچش برای مقاطع دایره‌ای توپر (τ_max=16T/πd³) محاسبه می‌شوند:

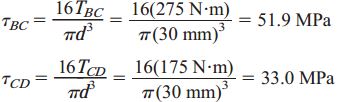
به دلیل بی‌اهمیت بودن جهت‌گیری تنش‌های برشی برای این مثال، تنها از قدر مطلق گشتاورهای به دست آمده برای انجام محاسبات بالا استفاده شد.

زاویه پیچش

زاویه پیچش بین چرخ‌دنده‌های B و C از جمع جبری زوایای پیچش بخش‌های قرار گرفته در بین این دو چرخ‌دنده به دست می‌آید. بنابراین:

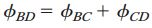
به منظور محاسبه هر یک از زوایای پیچش باید از ممان اینرسی قطبی سطح مقطع میله استفاده کنیم. این کمیت برای مقاطع دایره‌ای شکل به صورت زیر تعیین می‌شود:

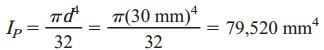
به این ترتیب، زوایای پیچش بخش‌های BC و CD به صورت زیر به دست می‌آیند:

توجه داشته باشید که در این مثال، زوایای پیچش دارای جهت‌های مخالف هستند. با جمع جبری این مقادیر به زاویه پیچش کل می‌رسیم:

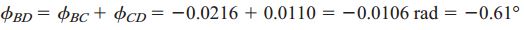
علامت منفی این زاویه نشان می‌دهد که چرخ‌دنده D از نمای سمت راست میله به صورت ساعت‌گرد دوران می‌کند. اکثر موارد تنها مقدار عددی زاویه پیچش مورد نیاز است. به همین دلیل، برای این مسئله معمولاً گفته می‌شود که زاویه پیچش بین چرخ‌دنده‌های B و D برابر با 0.61 درجه است. گاهی اوقات، به زاویه پیچش بین دو انتهای یک شَفت، «وایند‌آپ» (Wind-Up) گفته می‌شود.

توجه: فرآیند معرفی شده در این مسئله را می‌توانید برای میله‌های چندبخشی با قطر متفاوت یا مواد سازنده متفاوت نیز استفاده کنید. نکته مهم در این موارد این است که ابعاد میله و خواص مکانیکی باید در طول میله یکسان باشد.

مثال 2

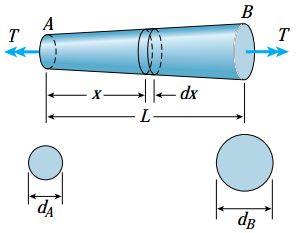
شکل زیر، میله مخروطی AB با سطح مقطع دایره‌ای توپر را نمایش می‌دهد. این میله تحت گشتاورهای پیچشی T قرار گرفته است. قطر AB به صورت خطی از مقدار dA در انتهای سمت چپ تا dB در انتهای سمت راست تغییر می‌کند. (dB را بزرگ‌تر از dA در نظر بگیرید.)

• الف) مقدار تنش برشی ماکسیمم در میله را تعیین کنید؟
• ب) رابطه تعیین زاویه پیچش در این میله را به دست آورید.

الف) تنش‌های برشی

کوچک‌ترین سطح مقطع این میله در انتهای A قرار دارد. با توجه به رابطه پیچش برای میله‌های دایره‌ای توپر (τ_max=16T/πd³)، تنش برشی ماکسیمم در این مقطع را محاسبه می‌کنیم:

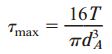
ب) زاویه پیچش

به دلیل ثابت بودن گشتاور پیچشی و تغییر پیوسته ممان اینرسی قطبی، به منظور تعیین زاویه پیچش از رابطه معرفی شده برای حالت دوم پیچش غیر یکنواخت استفاده می‌کنیم. در این مثال، قطر میله در فاصله x به صورت زیر مشخص می‌شود:

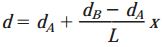
L: طول میله

با توجه به رابطه بالا، ممان اینرسی قطبی این میله به صورت زیر به دست می‌آید:

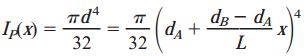
با جایگذاری رابطه بالا در رابطه زاویه پیچش برای حالت دوم، به انتگرال زیر می‌رسیم:

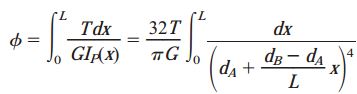
انتگرال بالا دارای فرم زیر است:

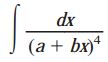
که در آن:

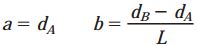
جواب این انتگرال برابر است با:

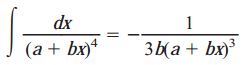
با در نظر گرفتن حدود 0 تا L و جایگذاری عبارت‌های معادل، به عبارت زیر می‌رسیم:

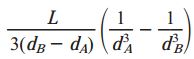
با قرار دادن جواب انتگرال در رابطه زاویه پیچش، خواهیم داشت:

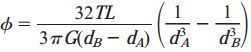
رابطه بالا برای تعیین زاویه پیچش در میله‌های مخروطی مورد استفاده قرار می‌گیرد. فرم ساده شده این رابطه به صورت زیر است:

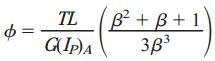
که در آن:

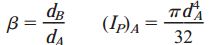
کمیت β، نسبت قطرهای دو انتهای میله و کمیت I_P)_A)، ممان اینرسی قطبی برای انتهای A را نمایش می‌دهد. در حالت خاص میله منشوری، β=1 است. در این حالت، زاویه پیچش از طریق رابطه φ=TL/G(I_P)_A به دست می‌آید. برای مقادیر β>1، زاویه پیچش کاهش می‌یابد. دلیل این موضوع، افزایش سختی پیچشی ناشی از قطر بیشتر میله در انتهای B است.

^^