مساله تقسیم بندی در بهینه سازی – به زبان ساده

در این مطلب، روش حل مساله تقسیم بندی در بهینه سازی بیان شده است. همچنین، پیاده‌سازی روش آموزش داده شده در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «سی» (C)، «جاوا» (Java)، «پایتون ۳» (Python 3) و «پی‌اچ‌پی» (PHP) انجام شده است. «مساله تقسیم بندی» (Partition Problem) یکی از انواع مسائل بهینه‌سازی است. در مساله تقسیم بندی، هدف تقسیم کردن مساله به دو زیر مجموعه به گونه‌ای است که مجموع مقادیر موجود در هر دو زیر مجموعه، با هم برابر باشد. مثال زیر در این راستا قابل توجه است:

arr[] = {1, 5, 11, 5}
Output: true 
The array can be partitioned as {1, 5, 5} and {11}

arr[] = {1, 5, 3}
Output: false 
The array cannot be partitioned into equal sum sets.

در ادامه، دو گام اساسی برای حل این مساله بیان شده‌اند.

1. مجموع آرایه را محاسبه کن. اگر مجموع عددی فرد باشد، دو زیر مجموعه با مجموع برابر وجود نخواهد داشت. بنابراین، مقدار False را بازگردان.
2. اگر مجموع عناصر آرایه زوج است، مجموع تقسیم بر ۲ را محاسبه و سپس، زیرمجموعه‌ای از آرایه با مجموع برابر با $$\frac{sum}{2}$$ را پیدا کن.

فیلم آموزش بهینه سازی مقید در متلب در فرادرس

کلیک کنید

گام اول ساده و گام دوم مهم و حیاتی است. برای پیاده‌سازی گام دوم می‌توان از راهکار بازگشتی یا برنامه‌نویسی پویا استفاده کرد.

راهکار بازگشتی برای حل مساله تقسیم بندی

در ادامه، راهکار بازگشتی برای پیاده‌سازی گام دوم بیان شده در بالا، ارائه شده است.

فیلم آموزش بهینه سازی چند هدفه در متلب در فرادرس

کلیک کنید

(isSubsetSum(arr, n, sum/2 تابعی است که اگر زیرمجموعه‌ای از آرایه [arr[0..n-1 با مجموع برابر با $$\frac{Sum}{2}$$ وجود داشت، مقدار True را باز می‌گرداند.

مساله isSubsetSum را می‌توان به دو زیر مسأله تقسیم کرد.

1. ()isSubsetSum بدون در نظر گرفتن آخرین عنصر (کاهش n به n-1)
2. isSubsetSum با در نظر گرفتن آخرین عنصر (کاهش $$\frac{Sum}{2}$$ با [arr[n-1 و n تا n-1)

اگر هر یک از دو زیرمسأله بالا مقدار true را بازگرداند، مقدار true را بازگردان.

isSubsetSum (arr, n, sum/2) = isSubsetSum (arr, n-1, sum/2) || isSubsetSum (arr, n-1, sum/2 - arr[n-1])

حل مساله تقسیم بندی به روش بازگشتی در ++C

حل مساله تقسیم بندی به روش بازگشتی در C

حل مساله تقسیم بندی به روش بازگشتی در جاوا

حل مساله تقسیم بندی به روش بازگشتی در پایتون ۳

حل مساله تقسیم بندی به روش بازگشتی در #C

حل مساله تقسیم بندی به روش بازگشتی در PHP

خروجی قطعه کدهای بالا به صورت زیر است.

Can be divided into two subsets of equal sum

پیچیدگی زمانی این روش در بدترین حالت از درجه (O(2ⁿ است. این روش دو احتمال (در نظر گرفتن یا نگرفتن) را برای هر یک از عناصر می‌سنجد.

راهکار برنامه نویسی پویا برای حل مساله تقسیم بندی

این مساله را می‌توان هنگامی که مجموع عناصر خیلی بزرگ نیست، با استفاده از «برنامه‌نویسی پویا» (Dynamic Programming) نیز حل کرد. می‌توان یک آرایه دوبُعدی [][]part با اندازه $$(\frac{sum}{2})*(n+1)$$ ساخت.

همچنین، می‌توان راهکار را به صورت پایین به بالا به گونه‌ای ساخت که هر ورودی دارای خصوصیات زیر باشد.

part[i][j] = true if a subset of {arr[0], arr[1], ..arr[j-1]} has sum 
equal to i, otherwise false

حل مساله تقسیم بندی با برنامه‌نویسی پویا در ++C/C

حل مساله تقسیم بندی با برنامه‌نویسی پویا در جاوا

حل مساله تقسیم بندی با برنامه‌نویسی پویا در پایتون ۳

حل مساله تقسیم بندی با برنامه‌نویسی پویا در #C

خروجی قطعه کدهای بالا به صورت زیر است.

Can be divided into two subsets of equal sum

نمودار زیر، مقادیر را در جدول تقسیم‌بندی نشان می‌دهد.

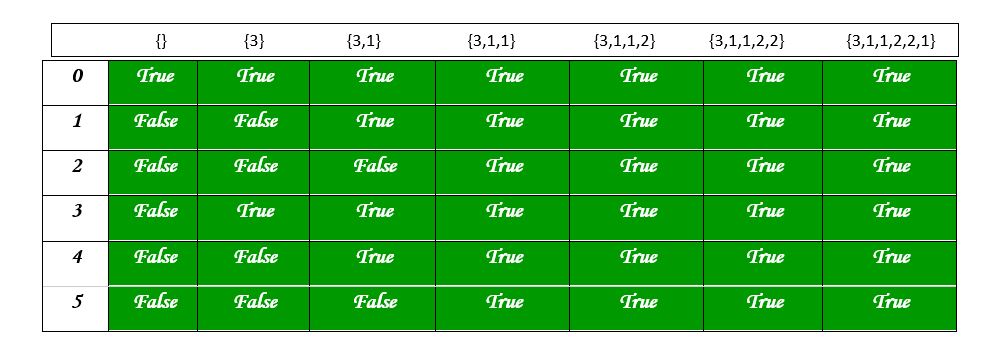
پیچیدگی زمانی این روش از درجه (O(sum*n و فضای کمکی آن از درجه (O(sum*n است. شایان توجه است که این روش برای آرایه‌هایی با مجموع بزرگ قابل استفاده نیست.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده
• الگوریتم جست و جوی دودویی در جاوا اسکریپت — به زبان ساده

^^