حل مساله بیشینه جریان – راهنمای جامع

در این مطلب، روش حل مساله بیشینه جریان (Maximum Flow Problem) بیان و راهکار بیان شده برای آن در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java)، «پایتون» (Python) و «سی‌شارپ» (#C) پیاده‌سازی شده است. یک گراف داده شده که نشانگر یک «شبکه جریان» (Flow Network) است و در آن، هر «یال» (Edge) دارای ظرفیت است. همچنین، دو راس s (مبدا | Source) و t (مقصد | Sink) در گراف داده شده است. هدف پیدا کردن بیشینه جریان ممکنی است که از s به t با در نظر داشتن محدودیت‌های زیر، شکل می‌گیرد.

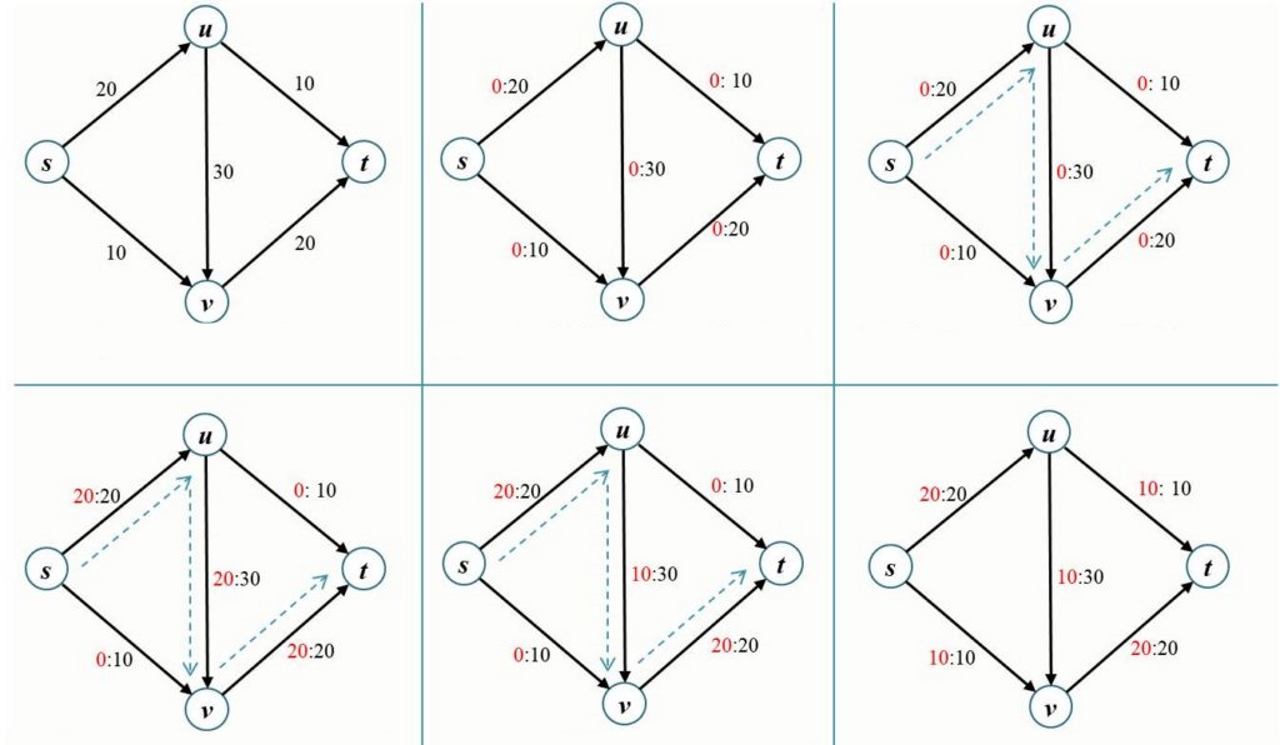
• جریان روی یک یال از ظرفیت داده شده روی آن یال سر ریز نمی‌کند.
• جریان ورودی برای هر راس، به جز s و t، مساوی با جریان خروجی است.

برای مثال، می‌توان گراف زیر را در نظر گرفت.

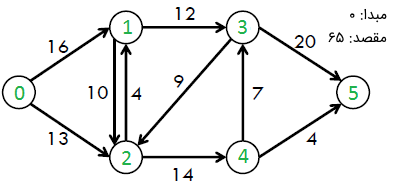
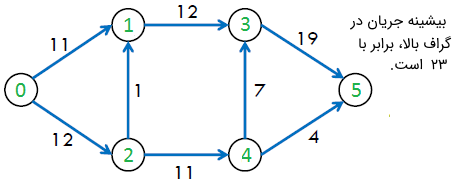
بیشینه جریان ممکن در گراف بالا برابر با ۲۳ است.

الگوریتم فورد–فالکرسون برای حل مساله بیشینه جریان

در ادامه، «الگوریتم فورد–فالکرسون» (Ford-Fulkerson Algorithm) برای حل مساله بیشینه جریان ارائه شده است.

•  با جریان اولیه ۰ شروع کن.
• تا هنگامی که یک مسیر تجمعی از مبدا به مقصد وجود دارد، این «مسیر-جریان» (Path-Flow) را به «جریان» اضافه کن.
• جریان را بازگردان.

پیچیدگی زمانی الگوریتم بالا از درجه O(max_flow * E)‎ است. هنگامی که یک مسیر تجمعی وجود داشته باشد، یک حلقه اجرا می‌شود. در بدترین حالت، ممکن است ۱ واحد جریان در هر تکرار اضافه شود. بنابراین، پیچیدگی زمانی برابر با O(max_flow * E)‎ خواهد شد.

پیاده‌سازی الگوریتم ساده بالا

برای پیاده‌سازی الگوریتم بالا، ابتدا باید مفهوم «گراف باقیمانده» (Residual Graph) تعریف شود که برای درک این پیاده‌سازی مورد نیاز است. گراف باقیمانده از یک شبکه جریان، گرافی است که جریان اضافی ممکن را نشان می‌دهد. اگر مسیری از مبدا به مقصد وجود داشته باشد، این امکان وجود دارد که جریان اضافه شود. هر یال از گراف دارای مقداری است که به آن ظرفیت باقیمانده گفته می‌شود. ظرفیت باقیمانده برابر با ظرفیت اصلی یال‌ها منهای جریان کنونی است. ظرفیت باقیمانده اساسا ظرفیت کنونی یال‌ها است.

فیلم آموزش نظریه گراف و کاربردها در فرادرس

کلیک کنید

اکنون، پیرامون جزئیات پیاده‌سازی صحبت خواهد شد. اگر هیچ یالی بین دو راس از گراف باقیمانده وجود نداشته باشد، ظرفیت باقیمانده برابر با ۰ است. می‌توان با توجه به اینکه هیچ جریان اولیه‌ای وجود ندارد، به گراف باقیمانده مقداردهی اولیه کرد. همچنین، ظرفیت باقیمانده اولیه برابر با ظرفیت اصلی است. برای پیدا کردن مسیر تجمعی، می‌توان از الگوریتم «جستجوی اول سطح» (Breadth-First Search) یا «جستجوی اول عمق» (Depth-First Search) استفاده کرد. در پیاده‌سازی زیر، برای پیدا کردن مسیر تجمعی از BFS استفاده شده است.

با استفاده از BFS، می‌توان بررسی کرد که آیا مسیری از مبدا به مقصد وجود دارد یا خیر. همچنین، BFS، آرایه parent[]‎ را می‌سازد. با استفاده از آرایه parent[]‎، پیمایش در مسیر یافته شده انجام و جریان احتمالی از طریق این مسیر با پیدا کردن ظرفیت باقیمانده در طول مسیر پیدا می‌شود. در ادامه، جریان مسیر یافت شده به جریان کلی اضافه می‌شود. نکته مهم آن است که به روز رسانی ظرفیت باقیمانده‌ها در گراف باقیمانده مورد نیاز است. جریان مسیر از همه یال‌ها در طول مسیر کسر می‌شود و جریان مسیر در امتداد یال‌های معکوس اضافه می‌شود. نیاز به اضافه کردن جریان مسیر در طول یال‌های معکوس است، زیرا ممکن است بعدا نیاز به ارسال جریان در جهت معکوس باشد.

حل مساله بیشینه جریان در ++C

حل مساله بیشینه جریان در جاوا

حل مساله بیشینه جریان در پایتون

حل مساله بیشینه جریان در #C

خروجی قطعه کدهای بالا به صورت زیر است.

The maximum possible flow is 23

پیاده‌سازی بالا از الگوریتم فورد–فالکرسون را «الگوریتم ادموندز کارپ» (Edmonds-Karp Algorithm) می‌گویند. ایده اصلی نهفته در پس استفاده از الگوریتم ادموندز کارپ، استفاده از BFS است؛ زیرا BFS همیشه مسیری با کمترین تعداد یال را انتخاب می‌کند.

هنگامی که BFS مورد استفاده قرار می‌گیرد، پیچیدگی زمانی بدترین حالت را می‌توان به O(VE²)‎ کاهش داد. پیاده‌سازی بالا از ارائه ماتریس مجاورت استفاده می‌کند و BFS دارای پیچیدگی زمانی از درجه O(V²)‎ است.

این مسأله با توجه به اینکه در بسیاری از موقعیت‌های عملی به وقوع می‌پیوندد، بسیار حائز است. از جمله مثال‌هایی برای مسأله بیشینه جریان می‌توان زد، افزایش حمل و نقل با توجه به محدودیت‌های ترافیکی داده شده و افزایش جریان بسته‌ها در شبکه‌های کامپیوتری است.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده

^^