مدار RLC سری — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس، درباره مدارهایی با یک عنصر ذخیره‌کننده انرژی (خازن یا سلف)، بحث کردیم. دیدیم که مدارهای مرتبه اول را می‌توان با معادلات دیفرانسیل مرتبه اول توصیف کرد. در این آموزش، مدارهایی را بررسی می‌کنیم که دو عنصر ذخیره انرژی دارند. این مدارها را مرتبه دوم می‌نامیم، زیرا پاسخ آن‌ها با معادلات دیفرانسیل مرتبه دوم توصیف می‌شود. مدارهای RLC، از مدارهای مرتبه دوم معروف هستند که سه عنصر پسیو مختلف در آن‌ها به‌کار رفته است. نمونه‌هایی از مدارهای مرتبه دوم در شکل ۱ نشان داده شده است.

شکل ۱ (الف) و (ب) مدارهای RLC هستند، درحالی که شکل‌های ۱ (ج) و (د) به‌ترتیب، مدارهای RL و RC را نشان می‌دهند. همان‌گونه که در شکل ۱ نشان داده شده است، ممکن است عناصر ذخیره کننده انرژی در یک مدار مرتبه دوم مشابه باشند (البته عناصری که نتوان آن‌ها را به یک عنصر معادل ساده کرد). مدار تقویت‌کننده عملیاتی با دو عنصر ذخیره‌ساز انرژی نیز یک مدار مرتبه دوم است. مشابه مدارهای مرتبه اول، مدارهای مرتبه دوم نیز می‌توانند چندین مقامت و منابع وابسته و مستقل داشته باشند.

تحلیل مدارهای مرتبه دوم، مشابه تحلیل مدارهای مرتبه اول است. در این آموزش، ابتدا مدار را با شرایط اولیه عناصر ذخیره کننده انرژی در نظر می‌گیریم. اگرچه ممکن است این مدارها شامل منابع وابسته باشند، اما بدون منابع مستقل هستند. همان‌گونه که انتظار داریم، مدارهای بدون منبع، دارای پاسخ طبیعی هستند. در مرحله بعد، مدارهای مرتبه دوم را با حضور منابع مستقل بررسی می‌کنیم که در این صورت، هم پاسخ گذرا و هم ماندگار خواهند داشت.

یافتن مقادیر اولیه و نهایی

شاید بتوان گفت مسئله اصلی که دانشجویان در رابطه با مدارهای مرتبه دوم با آن مواجه هستند، یافتن شرایط اولیه و نهایی متغیرهای مدار است. به‌دست آوردن مقادیر اولیه و نهایی $$v$$ و $$i$$ معمولاً برای دانشجویان آسان است، اما در یافتن مقادیر اولیه مشتتق آن‌ها ($$dv/dt$$ و $$di/dt$$) با مشکل مواجه می‌شوند. به همین دلیل، در این آموزش نحوه محاسبه $$v(0)$$، $$i(0)$$، $$dv(0)/dt$$، $$di(0)/dt$$، $$i(\infty)$$ و $$v(\infty)$$ را به‌صورت جداگانه بررسی خواهیم کرد. توجه کنید که $$v$$ ولتاژ خازن و $$i$$ جریان سلف است.

در تحلیل مدار، همیشه ابتدا باید پلاریته ولتاژ خازن و جهت جریان سلف را تعیین کنیم. همچنین، همیشه باید به خاطر داشت که ولتاژ خازن، پیوسته است:

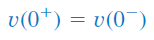
برای جریان یک سلف نیز همین گفته صادق است:

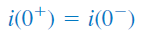
در رابطه‌های بالا، با فرض اینکه کلیدزنی در لحظه $$t=0$$ رخ دهد، $$t=0^-$$ درست لحظه قبل از کلیدزنی و $$t=0^+$$ لحظه بعد از آن را نشان می‌دهد.

بنابراین، برای یافتن شرایط اولیه ابتدا با اعمال روابط (۱-الف) و (۱-ب) متغیرهای ولتاژ خازن و جریان سلف را به‌دست می‌آوریم که به‌صورت ناگهانی تغییر نمی‌کنند.

مثال

کلید شکل 2، مدت زیادی در وضعیت بسته بوده است و در $$t=0$$ باز می‌شود. این متغیرها را پیدا کنید: (الف) $$i(0^+)$$ و $$v(0^+)$$؛ (ب) $$di(0^+)/dt$$ و $$dv(0^+)/dt$$؛ (ج) $$i(\infty)$$ و $$v(\infty)$$.

حل:

(الف) اگر کلید مدت زیادی قبل از $$t=0$$ در وضعیت بسته بوده باشد، یعنی در زمان $$t=0$$ به حالت ماندگار dc رسیده است. در حالت ماندگار dc، سلف به‌عنوان اتصال کوتاه و خازن مانند مدار باز عمل می‌کنند.

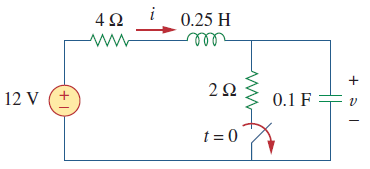
شکل 3 (الف)، مدار را در لحظه $$t=0^-$$ نشان می‌دهد. بنابراین:

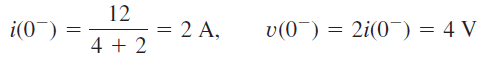
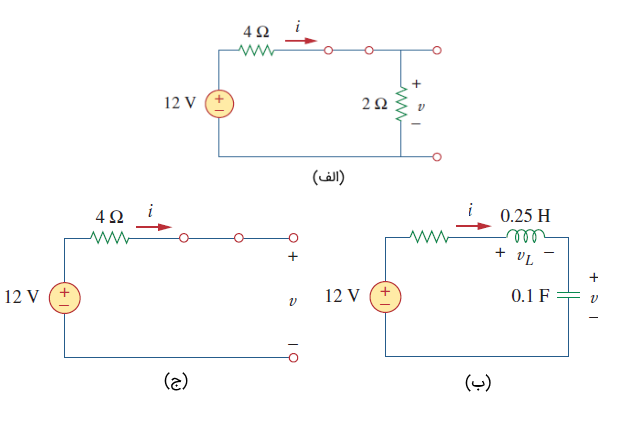
از آن‌جایی که جریان سلف و ولتاژ خازن نمی‌توانند به‌صورت ناگهانی تغییر کنند، داریم:

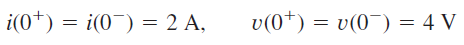
(ب) در $$t=0^+$$، کلید باز است که مدار معادل آن در شکل ۳(ب) نشان داده شده است. با توجه به شکل، جریان مشابهی از سلف و خازن می‌گذرد. بنابراین:

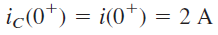
از آن‌جایی که $$C dv/dt=i_C$$، داریم:

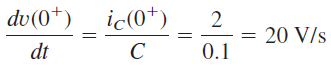
اکنون می‌توانیم $$v_L$$‌ را با استفاده از KVL در حلقه شکل 3(ب) به‌دست آوریم:

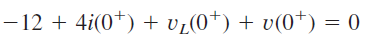
یا

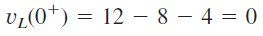
بنابراین، از آن‌جایی که $$L di/dt=v_L$$ داریم:

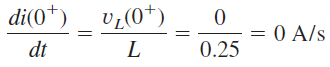
(ج) برای $$t>0$$، مدار به حالت گذرا می‌رود. اما، وقتی $$t \to \infty$$، مدار مجدداً به حالت ماندگار می‌رسد. در این حالت، سلف به‌عنوان اتصال کوتاه و خازن مانند مدار باز عمل می‌کند. بنابراین، طبق شکل ۳(ج)، داریم:

مدار RLC بدون منبع

درک درست پاسخ طبیعی مدار RLC سری، برای طراحی فیلتر و شبکه‌های مخابراتی امری ضروری است.

مدار RLC شکل 4 را در نظر بگیرید. این مدار با انرژی ذخیره شده خازن و سلف تحریک می‌شود.

انرژی را برحسب ولتاژ اولیه خازن $$V_0$$ و جریان اولیه سلف $$I_0$$ نمایش می‌دهیم. بنابراین، در $$t=0$$ داریم:

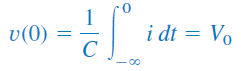
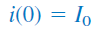
اعمال KVL به حلقه شکل ۴، منجر به رابطه زیر خواهد شد:

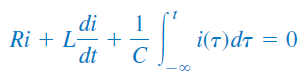
برای حذف انتگرال از رابطه بالا، از آن نسبت به $$t$$ انتگرال می‌گیریم و آن را بازنویسی می‌کنیم:

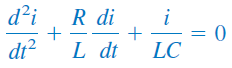
معادله بالا، یک معادله دیفرانسیل مرتبه دوم است و به همین دلیل، مدارهای RLC، مدارهای مرتبه دوم نامیده می‌شوند.

برای به‌دست آوردن پاسخ مدار، باید معادله (۴) را حل کنیم. برای حل یک معادله دیفرانسیل مرتبه دوم، باید دو شرط اولیه داشته باشیم (مثلاً مقدار اولیه $$i$$ و مشتق اول آن یا مقادیر اولیه $$i$$ و $$v$$). مقدار اولیه $$i$$ از رابطه (2-ب) به‌دست می‌آید. مقدار اولیه مشتق $$i$$ نیز از معادلات (۲-الف) و (۳) قابل دست‌یابی است:

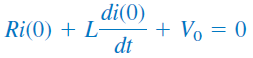
یا

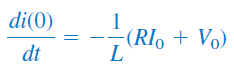
اکنون با دو شرط اولیه روابط (2-ب) و (5)، می‌توان معادله (۴) را حل کرد. در آموزش مدار مرتبه اول دیدیم که پاسخ مدار مرتبه اول به فرم نمایی است:

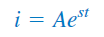
که در آن، $$A$$ و $$s$$ ثابت‌هایی هستند که با توجه مدار تعیین می‌شوند. با جایگذاری معادله (۶) در معادله (۴) و انجام مشتق‌گیری‌ها، به رابطه زیر می‌رسیم:

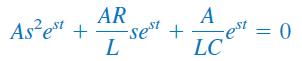
یا

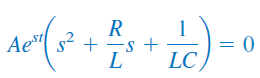
از آن‌جایی که $$i=Ae^{st}$$، به‌عنوان حل فرض شده است، عبارت داخل پرانتز را برابر صفر قرار می‌دهیم:

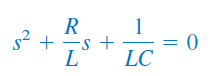
معادله فوق، معادله مشخصه (Characteristic equation)‌ معادله دیفرانسیل (۴) نامیده می‌شود، زیرا ریشه‌های این معادله، مشخصه $$i$$ را تعیین می‌کنند. دو ریشه معادله (۸) به‌صورت زیر هستند:

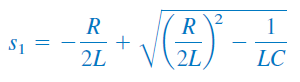
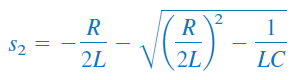
ریشه‌های بالا را مي‌توانیم به فرم فشرده‌تر زیر نیز بیان کنیم:

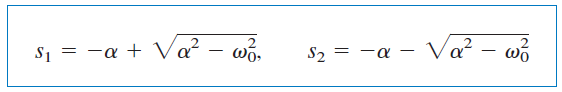
که در آن:

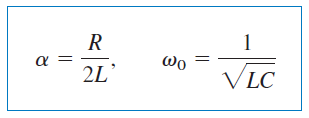
از آن‌جایی که ریشه‌های $$s_1$$ و $$s_2$$ مربوط به پاسخ فرکانسی مدار هستند، به آن‌ها فرکانس‌های طبیعی (Natural frequencies) می‌گوییم که برحسب نپر بر ثانیه ($$Np/s$$) اندازه‌گیری می‌شوند. $$\omega _0$$ را فرکانس تشدید یا رزونانس (Resonant response) یا فرکانس طبیعی نامیرا می‌نامند و برحسب رادیان بر ثانیه ($$rad/s$$) بیان می‌کنند. پارامتر $$\alpha$$، فرکانس نپر (Neper frequency) یا ضریب میرایی (Damping factor) نامیده می‌شود و واحد آن، نپر بر ثانیه است. معادله (۸) را می‌توان برحسب پارامترهای $$\alpha$$ و $$\omega _0$$ به‌صورت زیر نوشت:

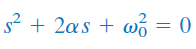
متغیرهای $$s$$ و $$\omega _0$$، کمیت‌های مهمی هستند که در ادامه درباره آن‌ها بحث خواهیم کرد.

دو مقدار $$s$$ در رابطه (۱۰) دو حل ممکن را برای $$i$$ نشان می‌دهند که هر کدام به فرم معادله (۶) هستند:

از آن‌جایی که معادله (۴) خطی است، هر ترکیب خطی از دو پاسخ $$i_1$$ و $$i_2$$ نیز پاسخی برای (۴) خواهد بود. ارائه یک حل کامل برای معادله (۴) نیازمند ترکیب $$i_2$$ و $$i_2$$ است. بنابراین، پاسخ طبیعی مدار RLC‌ سری به‌صورت زیر است:

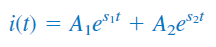
که در آن، ثابت‌های $$A_1$$ و $$A_2$$ از مقادیر اولیه $$i(0)$$ و $$di(0)/dt$$ در معادلات (۲-ب) و (۵) به‌دست می‌آیند.

با توجه به رابطه (۱۰)، سه نوع پاسخ مختلف وجود خواهد داشت:

1. اگر $$\alpha> \omega _0$$، پاسخ فرامیرا (Overdamped)‌ است.
2. اگر $$\alpha= \omega _0$$، پاسخ میرای بحرانی (Critically damped) است.
3. اگر $$\alpha< \omega _0$$، پاسخ فرومیرا (Underdamped) است.

در ادامه، هر یک از این پاسخ‌ها را بررسی می‌کنیم.

پاسخ فرامیرا ($$\alpha > \omega _0$$)

از معادلات (۹) و (۱۰) می‌توان نتیجه گرفت اگر $$\alpha> \omega _0$$، آن‌گاه $$C>4L/R^2$$. وقتی چنین وضعیتی رخ دهد، هر دو ریشه $$s_1$$ و $$s_2$$ منفی و حققیقی خواهند بود. در نتیجه، پاسخ مدار به‌صورت زیر است:

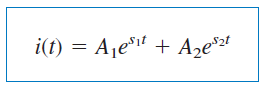
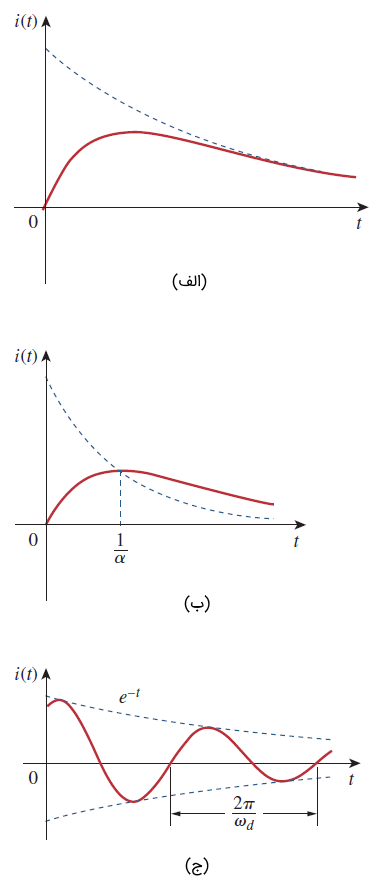
از رابطه بالا مشخص است که پاسخ با گذشت زمان به صفر میل می‌کند. شکل ۵(الف)، پاسخ فرامیرا را نشان می‌دهد.

پاسخ میرای بحرانی ($$\alpha = \omega _0$$)

وقتی $$\alpha = \omega _0$$، آن‌گاه $$C=4L/R^2$$ و داریم:

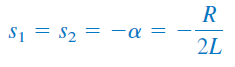
در این حالت، می‌توان از  معادله (۱۳) نتیجه گرفت:

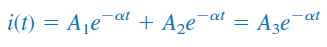
که در آن، $$A_3=A_1+A_2$$. معادله فوق نمی‌تواند پاسخ مدار باشد، زیرا $$A_3$$ فقط در یکی از دو شرط اولیه صدق می‌کند. اما مشکل کجاست؟ فرض اولیه‌مان که گفتیم پاسخ مدار نمایی است در ین مورد اشتباه است. بنابراین، به معادله (۴) باز می‌گردیم. وقتی $$\alpha =\omega _0=R/2L$$، معادله (۴) به‌شکل زیر در خواهد آمد:

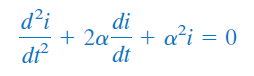
یا

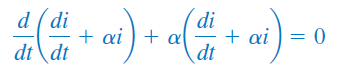
اگر عبارت زیر را در نظر بگیریم:

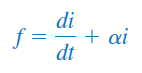
معادله (۱۶) را می‌توان به‌صورت زیر نوشت:

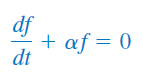
که یک معادله دیفرانسیل مرتبه اول با حل $$f=A_1e^{-\alpha t}$$ است ($$A_1$$ ثابت است). بنابراین، معادله (۱۷) به‌شکل زیر خواهد بود:

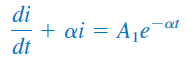
یا

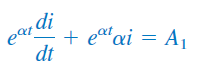
معادله فوق را می‌توان به‌صورت زیر نوشت:

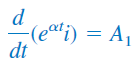
اگر از طرفین رابطه بالا انتگرال بگیریم، خواهیم داشت:

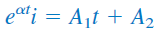
یا

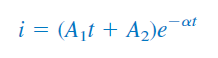
که در آن، $$A_2$$ نیز یک ثابت است. بنابراین، پاسخ طبیعی مدار میرای بحرانی، مجموع دو عبارت است: نمایی منفی و حاصل‌ضرب یک نمایی منفی و جمله خطی. به عبارت دیگر:

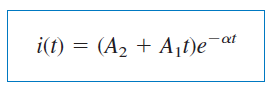
پاسخ یک مدار میرای بحرانی در شکل ۵(ب) نشان داده شده است. در حقیقت، شکل ۵(ب) نمودار $$i(t)=te^{-\alpha t}$$ است که در $$t=1/ \alpha$$ (یک ثابت زمانی) به حداکثر مقدار $$e^{-1}/\alpha$$ می‌رسد، سپس کاهش می‌یابد تا به صفر برسد.

پاسخ فرومیرا ($$\alpha < \omega _0$$)

اگر $$\alpha < \omega _0$$، آن‌گاه $$C<4L/R^2$$ و ریشه‌ها را می‌توان به‌صورت زیر نوشت:

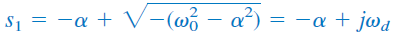
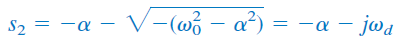
که در آن، $$j=\sqrt{-1}$$ است و $$\omega _d = \sqrt {\omega _0^2-\alpha ^2}$$ فرکانس میرایی (Damping frequency) نامیده می‌شود. هر دو فرکانس $$\omega _0$$ و $$\omega _d$$، فرکانس طبیعی هستند، زیرا به یافتن پاسخ طبیعی مدار کمک می‌کنند. فرکانس $$\omega _0$$ اغلب فرکانس طبیعی فرومیرا (Underdamped natural frequency) نامیده می‌شود. پاسخ طبیعی به‌صورت زیر است:

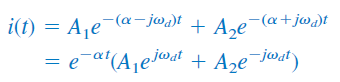
اتحاد اویلر زیر را در نظر بگیرید:

با استفاده از این روابط، پاسخ طبیعی مدار را می‌توانیم به‌صورت زیر بنویسیم:

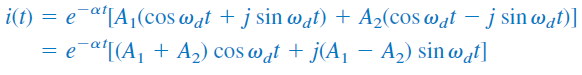
اگر ثابت‌های $$(A_1+A_2)$$ و $$j(A_1-A_2)$$ را با $$B_1$$ و $$B_2$$ نشان دهیم، پاسخ نهایی مدار به‌صورت زیر در می‌آید:

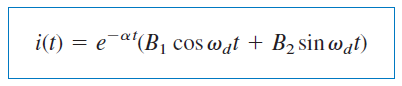
با حضور توابع سینوس و کسینوس واضح است که پاسخ طبیعی در این حالت، به‌صورت نمایی میرا خواهد شد و ماهیت آن نوسانی است. ثابت زمانی و دوره تناوب پاسخ به‌ترتیبب، $$1/\alpha$$ و $$T=2 \pi / \omega _d$$ هستند. شکل 5(ج) یک پاسخ فرومیرا را نشان می‌دهد.

با محاسبه جریان $$i(t)$$ سلف، در مدار RLC‌ سری، سایر کمیت‌های مدار مانند ولتاژ تک‌تک عناصر به‌دست می‌آیند. برای مثال، ولتاژ مقاومت برابر با $$v_R=Ri$$ است و ولتاژ سلف از رابطه $$v_L=L di/dt$$ محاسبه می‌شود. جریان $$i(t)$$ سلف به دلیل مزایای معادله (۱-ب) به‌عنوان متغیر کلیدی انتخاب شده است.

به‌عنوان یک جمع‌بندی، می‌توان موارد زیر را برای مدارهای RLC بدون منبع بیان کرد:

1. رفتار مدار، میرا بوده و بیان‌گر اتلاف تدریجی انرژی ذخیره شده اولیه است. این میرایی به‌دلیل حضور مقاومت $$R$$ در مدار است. ضریب میرایی $$\alpha$$، نرخ میرایی پاسخ را تعیین می‌کند. اگر $$R=0$$‌ باشد، آن‌گاه $$\alpha =0$$ خواهد بود و یک مدار LC با فرکانس طبیعی نامیرای $$1/ \sqrt{LC}$$ داریم. از آن‌جایی که در این حالت، $$\alpha < \omega _0$$، پاسخ نوسانی نیز است. این مدار را بدون تلفات می‌نامند، زیرا عنصر میراکننده یا تلف‌کننده توان ($$R$$) در آن وجود ندارد. با توجه به مقدار $$R$$ ممکن است پاسخ نامیرا، فرامیرا، میرای بحرانی یا فرومیرا باشد.
2. اگر دو عنصر ذخیره‌کننده انرژی در مدار وجود داشته باشد، پاسخ نوسانی است. با وجود دو عنصر $$L$$ و $$C$$، انرژی بین آن‌ها مباده می‌شود. نوسان میرا، در حالت پاسخ فرومیرا رخ می‌دهد. این مورد، از توانایی عناصر ذخیره‌ساز انرژی $$L$$ و $$C$$ در مبادله انرژی نشئت می‌گیرد.
3. از شکل ۵ مشخص است که شکل موج پاسخ‌ها با هم تفاوت دارد. در حالت کلی، پیدا کردن تفاوت پاسخ های فرامیرا و میرای بحرانی از روی شکل آن‌ها کار دشواری است. پاسخ میرای بحرانی بین پاسخ‌های فرومیرا و فرامیرا است و سریع‌تر از آن دو کاهش پیدا می‌کند. در شرایط اولیه برابر، پاسخ فرامیرا طولانی‌ترین زمان نشست را دارد، زیرا زمان اتلاف انرژی ذخیره شده در آن بیش‌تر از دو پاسخ دیگر است. اگر بخواهیم پاسخ، بدون نوسان در سریع‌ترین زمان ممکن به مقدار نهایی برسد، مدار میرای بحرانی بهترین گزینه است.

پاسخ پله مدار RLC‌ سری

همان‌گونه که در آموزش‌های قبلی مجله فرادرس دیدیم، پاسخ پله با اعمال ناگهانی یک منبع dc به مدار به‌دست می‌آید.

مدار RLC شکل ۶ را در نظر بگیرید.

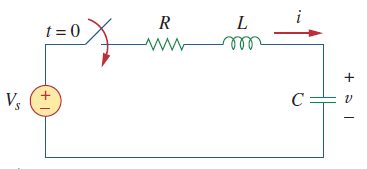
با اعمال KVL به مدار بالا برای $$t>0$$، داریم:

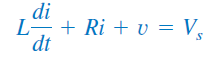
از آن‌جایی که $$i=C dv/dt$$، معادله (27) را می‌توان به‌صورت زیر بازنویسی کرد:

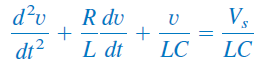
که شبیه معادله (۴) است. به‌طور خاص، ضرایب دو معادله با هم برابر هستند (که در تعیین پارامترهای فرکانس مهم است) و متغیرهای آن‌ها فرق دارند. بنابراین، معادله مشخصه مدار RLC سری تحت تاثیر منبع dc قرار نمی‌گیرد.

پاسخ معادله (۲۸)، دو بخش دارد: پاسخ گذرای $$v_t(t)$$ و پاسخ حالت ماندگار $$v_{ss}(t)$$:

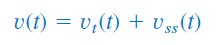
پاسخ گذرای $$v_t(t)$$ بخشی از پاسخ کامل است که در طول زمان کاهش می‌یابد. فرم پاسخ گذرا مشابه پاسخی است که برای مدار RLC بدون منبع به‌دست آمد. بنابراین، پاسخ گذرای $$v_t(t)$$ برای سه حالت فرامیرا، میرای بحرانی و فرومیرا به‌ترتیب، به‌‌صورت زیر است:

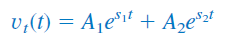
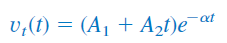
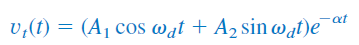
پاسخ حالت ماندگار، مقدار نهایی $$v(t)$$ است. در شکل 6، مقدار نهایی ولتاژ خازن برابر با ولتاژ $$V_s$$ منبع است. بنابراین:

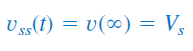
در نتیجه، پاسخ کامل برای موارد فرامیرا، میرای بحرانی و فرومیرا به‌صورت زیر است:

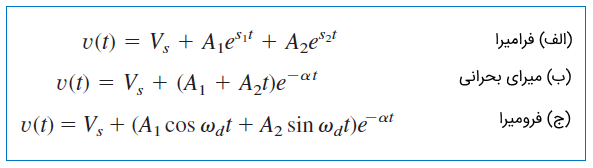
مقادیر ثابت $$A_1$$ و $$A_2$$، از شرایط اولیه $$v(0)$$ و $$dv(0)/dt$$ به‌دست می‌آیند.‌ با محاسبه مقدار $$v$$ می‌توانیم $$i$$ را نیز به‌دست آوریم. با استفاده از این جریان، می‌توانیم ولتاژ سلف و مقاومت را نیز تعیین کنیم.

مدارهای مرتبه دوم عمومی

اکنون که نمونه‌ای از مدارهای مرتبه دوم را بررسی کردیم، می‌توانیم روند کلی محاسبه پاسخ مدارهای مرتبه دوم را بیان کنیم.

فرض کنید یک مدار مرتبه دوم در اختیار داریم و می‌خواهیم پاسخ پله $$x(t)$$ (جریان یا ولتاژ) آن را به‌دست آوریم. برای این کار، باید مراحل زیر را انجام داد:

1. ابتدا شرایط اولیه $$x(0)$$ و $$dx(0)/dt$$ و مقدار نهایی $$x(\infty)$$‌ را تعیین کنید.
2. همه منابع مستقل را حذف کرده و فرم پاسخ گذرای $$x_t(t)$$ را با اعمال KCL یا KVL به‌دست آورید. بعد از آنکه معادله دیفرانسیل مرتبه دوم را به‌دست آوردید، ریشه‌های معادله مشخصه آن را تعیین کنید.
3. پاسخ حالت ماندگار را به‌صورات زیر محاسبه کنید:

   

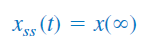
4. پاسخ کامل برابر با مجموع پاسخ گذرا و پاسخ حالت ماندگار است:

   

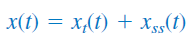
5. در نهایت، ثابت‌های پاسخ گذار را با اعمال شرایط اولیه $$x(0)$$ و $$dx(0)/dt$$ از گام اول، محاسبه کنید.

روند بالا را می‌توانیم به مدارهای مرتبه دوم شامل تقویت‌‌کننده‌های عملیاتی نیز اعمال کنیم.

در صورتی که مباحث بیان شده برای شما مفید بوده و می‌خواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد می‌کنیم به آموزش‌های زیر مراجعه کنید:

• دو قطبی در مدارهای الکتریکی — به زبان ساده
• تزویج در مدارهای الکتریکی — مفاهیم اصلی

^^