انتگرال ریمان استیلتیس (Riemann Stieltjes) – مفاهیم و کاربردها

در ریاضیات، «انتگرال ریمان-استیلت‌یس» (Riemann–Stieltjes integral)، تعمیم «انتگرال ریمان» (Riemann Integral) محسوب می‌شود .انتگرالی که در حساب دیفرانسیل و انتگرال به کار می‌رود همان انتگرال ریمان است که براساس جمع‌های ریمانی بدست می‌آید. این انتگرال توسط «توماس جونز استیلت‌یس» (Thomas Joannes Stieltjes) با استفاده از ایده «برنارد ریمان» (Bernard Riemann) در مقاله‌ای در سال ۱864 معرفی شد. یکی از کاربردهای این انتگرال در محاسبه انتگرال لبگ است که توانست مفاهیم و قضایای آماری را با پشتوانه ریاضی همراه کند.

برای آشنایی بیشتر با مفهوم انتگرال تابع، بهتر است ابتدا مطلب انتگرال — به زبان ساده را خوانده باشید زیرا مفهوم انتگرال در هر دو شیوه تقریبا مشابه یکدیگر است. همچنین برای درک مفهوم مشتق و پیوستگی، مطالعه مطالب مشتق — به زبان ساده و پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده خالی از لطف نیست.

انتگرال ریمان-استیلت‌یس

اگر f و g دو تابع حقیقی-مقدار باشند، انتگرال ریمان-استیلت‌یس تابع f برحسب تابع g در فاصله a تا b به صورت زیر نوشته می‌شود:

$$\large \int_a^bf(x)\;dg(x)$$

برای محاسبه این انتگرال ابتدا باید فاصله a تا b‌ را افراز کنیم. فرض کنید

فیلم آموزش تابع زتا و فرضیه صفرهای ریمان (رایگان) در فرادرس

کلیک کنید

مجموعه P به صورت یک افراز از فاصله a تا b به شکل زیر ایجاد شده است.

$$\large P=\{a=x_0$$

در این صورت اگر افراز را ظریف و ظریف‌تر بکنیم بطوری که طول بزرگترین فاصله به سمت صفر میل کند، انتگرال ریمان-استیلت‌یس را به صورت حد مجموع زیر می‌توان نشان داد.

$$\large S(P,f,g)=\sum _{i=0}^{n-1}f(c_{i})(g(x_{i+1})-g(x_{i}))$$

بطوری که $$c_i$$ مقداری در فاصله iام در بین $$[x_i,x_{i+1}]$$ قرار دارد. به این ترتیب f را «انتگرال‌ده» (Integrand) و g را «انتگرال‌گیر» (Integrator) می‌گویند.

منظور از حد این جمع، همان مقدار انتگرال است که اگر آن را با A نشان دهیم با توجه به تعریف حد، می‌توان نوشت:

$$\large \forall\; \epsilon >0 \;\;\exists\; \delta >0,\;\; Norm(P)<\delta,\;\; |S(P,f,g)-A|<\epsilon$$

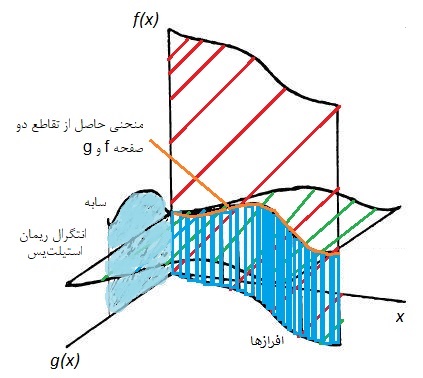
تفسیر هندسی انتگرال ریمان-استیلت‌یس

فرض کنید، در مختصات سه بعدی ($$x,g(x),f(x)$$) منحنی $$g(x)$$ و $$f(x)$$ ترسیم شده‌اند. اگر صفحه حاصل از منحنی f و x را با صفحه حاصل از منحنی g و x تقاطع دهیم، در صفحه سه بعدی منحنی جدیدی حاصل می‌شود. با محاسبه سایه این مستطیل‌هایی که با طول f و  عرضی به اندازه افرازهای g ایجاد شده‌اند، روی صفحه (دیوار) حاصل از f و g انتگرال ریمان-استیلت‌یس بدست می‌آید.

شرط وجود انتگرال ریمان استیلت‌یس با جمع‌های داربو

انتگرال ریمان-استیلت‌یس را می‌توان براساس جمع‌های «داربو» ( Jean Gaston Darboux) نیز نوشت. برای افراز P‌ و تابع غیرنزولی g در فاصله $$[a,b]$$ جمع بالایی داربو را نسبت به g به صورت زیر می‌نویسیم.

$$\large U(P,f,g)=\sum _{i=1}^{n}\,\,[\,g(x_{i})-g(x_{i-1})\,]\,\sup _{x\in [x_{i-1},x_{i}]}f(x)$$

همینطور نیز جمع پایینی به شکل زیر نوشته می‌شود:

$$\large L(P,f,g)=\sum _{i=1}^{n}\,\,[\,g(x_{i})-g(x_{i-1})\,]\,\inf _{x\in [x_{i-1},x_{i}]}f(x)$$

نکته:  منظور از سپریمم یا sup، کمترین کران بالا و اینفیمم یا inf نیز بزرگترین کران پایین برای تابع f در بازه $$[x-{i-1},x-i]$$ است. لزوما مقدار sup یا inf برای تابع f در برد این تابع قرار ندارند.

می‌توان گفت که انتگرال ریمان-استیلت‌یس زمانی وجود دارد که حد تفاضل این دو جمع برابر با صفر باشد و برعکس. یعنی اگر انتگرال ریمان-استیلت‌یس وجود داشته باشد آنگاه حد تفاضل این دو جمع برابر با صفر است. در این حالت می‌توان نوشت:

$$\large \forall\; \epsilon >0 \;\;\exists\; \delta >0,\;\; Norm(P)<\delta,\;\; |U(P,f,g)-L(P,f,g)|<\epsilon$$

و اگر انتگرال ریمان-استیلت‌یس f نسبت به g روی بازه a تا b وجود داشته باشد، آنگاه

$$\large \lim _{\operatorname {norm} (P)\to 0}[\,U(P,f,g)-L(P,f,g)\,]=0$$

کاربردها

با توجه به تعریف عامی که انتگرال ریمان-استیلت‌یس دارد، می‌توان بسیاری از انواع انتگرال‌های دیگر را برحسب آن نوشت و از خصوصیاتش استفاده کرد.

فیلم آموزش محاسبات انتگرال با متلب و میپل MATLAB و Maple در فرادرس

کلیک کنید

انتگرال ریمان

فرض کنید که $$g(x)=x$$ پس انتگرال ریمان-استیلت‌یس، به صورت انتگرال ریمان درخواهد آمد. یعنی

$$\large \int_a^bf(x)dx$$

به همین شکل فرم انتگرال f بر حسب x که بطور معمول به انتگرال ریمان شهرت دارد را می‌توان برحسب تعریف انتگرال ریمان-استیلت‌یس براساس جمع نوشت. این فرم جمع را «جمع ریمانی» (Riemann sum) تابع f می‌گویند.

 $$\large {\displaystyle \sum _{i=0}^{n-1}f(t_{i})\left(x_{i+1}-x_{i}\right)}$$

انتگرال با تابع مشتق‌پذیر $$g(x)$$

اگر تابع انتگرال‌گیر در انتگرال ریمان-استیلت‌یس، مشتثق‌پذیر روی اعداد حقیقی باشد، می‌توان بین انتگرال ریمان-استیلت‌یس و انتگرال ریمان رابطه زیر را در نظر گرفت.

$${\large \displaystyle \int _{a}^{b}f(x)dg(x)=\int _{a}^{b}f(x)g'(x)dx}$$

البته در اینجا فرض بر این است که تابع f برحسب g انتگرال‌پذیر ریمان-استیلت‌یس است و g نیز انتگرال مشتق خود است. در این حالت شرط مشتق‌پذیری تابع g را می‌توان با شرط «پیوستگی مطلق» (Absolute Contentious) جایگزین کرد. پیوستگی مطلق به این معنی است که تابع g در بعضی از نقاط، ناپیوسته یا دارای مشتق برابر با صفر است ولی اندازه چنین نقاطی صفر است. یا به معنی دیگر تابع g تقریبا همه جا پیوسته است به جز در نقاطی که اندازه آن‌ها براساس تابع g صفر است.

واحدهای خطی یک‌سو شده  (REULU- Rectified Linear Unit)

فرض کنید در بحث «شبکه عصبی» (Neural Network)، تابع RELU برابر با $$g(x)=max\{0,x\}$$ باشد. آنگاه انتگرال ریمان-استیلت‌یس برای تابع f به صورت زیر در خواهد آمد:

$$\large {\displaystyle \int _{a}^{b}f(x)dg(x)=\int _{\max\{a,0\}}^{\max\{b,0\}}f(x)dx}$$

بطوری که انتگرال سمت راست همان انتگرال ریمان معمولی است. از تابع RELU در شبکه‌های عصبی مصنوعی، بخصوص بخش‌های «بینایی ماشین» (Computer Vision)، «تشخیص گفتار» (Speech Recognition) و «شبکه‌های عصبی عمیق» (Deep Neural Nets) استفاده می‌شود.

کاربرد در احتمال

فرض کنید که تابع g همان تابع توزیع احتمال تجمعی (Cumulative Probability Distribution Function) متغیر تصادفی X باشد.از طرفی می‌دانیم که X دارای تابع چگالی نیز هستد (پس انتگرال تابع چگالی همان تابع احتمال تجمعی است و مشتق تابع احتمال تجمعی هم برابر با تابع چگالی خواهد بود) پس شرط مربوط به یپوستگی مطلق برای g برقرار است. از طرف دیگر فرض کنید که f نیز همان تابعی باشد که قصد داریم امید-ریاضی آن را محاسبه کنیم. براساس انتگرال ریمان-استیلت‌یس خواهیم داشت:

$$\large E(f(x))=\int_{-\infty}^{\infty}f(x)dg(x)$$

این رابطه با توجه به وجود تابع احتمال تجمعی برای متغیر تصادفی X توسط انتگرال ریمان-اشتیلجس قابل محاسبه است. همچنین می‌توان از این انتگرال در زمانی که حتی متغیر تصادفی X گسسته است کمک گرفت و امید ریاضی را با توجه به تعریف جمع برای این انتگرال بدست آورد. به همین ترتیب می‌توان برای گشتاورهای متغیر تصادفی X نیز، محاسبات را برحسب این انتگرال بیان کرد.

$$\large {\displaystyle E(X^{n})=\int _{-\infty }^{\infty }x^{n}\,dg(x)}$$

بنابراین تعریف امید-ریاضی برای متغیرهای تصادفی که ممکن است تابع چگالی آن‌ها فرم بسته‌ای نداشته باشد، محاسبه کرد البته شرط پیوستگی مطلق برای تابع توزیع تجمعی آن باید برقرار باشد. البته اگر تابع g مشتق‌پذیر در دامنه‌اش باشد می‌توان از فرم ساده‌تر زیر کمک گرفت که همان تعریف امید ریاضی برحسب انتگرال ریمان است.

$$\large E(f(x))=\int_{-\infty}^{\infty}f(x)dg(x)=\int_{-\infty}^{\infty}f(x)g'(x)dx$$

اگر مطلب بالا برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس دبیرستان
• مجموعه آموزش‌های ریاضی و فیزیک
• آموزش ریاضیات عمومی ۱
• انتگرال به زبان ساده — بخش دوم: روش‌های محاسبه
• انتگرال گیری جزء به جزء — به زبان ساده
• محاسبه انتگرال به روش تغییر متغیر — از صفر تا صد
• پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده
• قضیه مقدار میانی (Intermediate Value Theorem) — به زبان ساده

^^