تعیین رابطه بین مدول الاستیسیته و مدول برشی با مفاهیم پیچش – راهنمای کاربردی
در مباحث «پیچش و تغییر شکلهای ناشی از آن»، «تحلیل میلههای تحت پیچش»، «پیچش غیر یکنواخت» و «تعیین مؤلفههای تنش و کرنش در بارگذاری پیچشی»، به معرفی مفاهیم اساسی پیچش و روابط مورد نیاز برای تعیین مؤلفههای آن در میلهها و لولههای دایرهای پرداختیم. یکی از کاربردهای مهم روابط ارائه شده در این مطالب، به دست آوردن رابطهای بین مدول الاستیسیته E و مدول برشی G است. در این مقاله، نحوه تعیین رابطه بین E و G را با استفاده از روابط معرفی شده برای بارگذاری پیچشی تشریح خواهیم کرد.
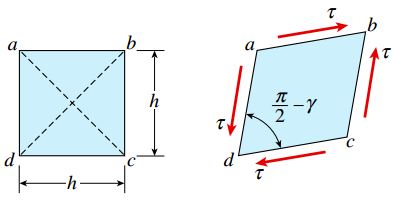
شکل زیر، المان تنش abcd را نمایش میدهد. صفحه جلویی abcd به شکل یک مربع در نظر گرفته میشود. طول اضلاع این مربع، h است. در صورت اعمال تنشهای برشی τ و ایجاد برش خالص در این المان، صفحه جلویی آن به شکل یک لوزی درمیآید. پس از این فرآیند، طول اضلاع المان تغییریافته برابر با h و تنش برشی ایجاد شده در آن γ=τ/G خواهد بود. به دلیل ایجاد اعوجاج، طول قطر bd افزایش و طول قطر ac کاهش مییابد.
طول قطر bd با حاصلضرب طول اولیه آن در ضریب 1+εmax برابر است:
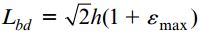
Lbd: طول قطر bd المان؛ h: طول اضلاع المان تنش؛ 0.5(2)*h: طول اولیه قطر bd المان؛ εmax: تنش نرمال در راستای 45 درجه
با در نظر گرفتن هندسه المان تغییریافته میتوان رابطه بین کرنش برشی γ و طول قطر bd را تعیین کرد. به این منظور، المان مثلثی abd را مطابق شکل زیر در نظر میگیریم. این المان، نصفِ المان تغییریافته را نمایش میدهد. طول ضلع bd برابر با Lbd و طول دیگر اضلاع برابر با h است. زاویه adb نیز با نصف زاویه adc یا π/4-γ/2 برابری میکند. مقدار زاویه abd نیز مشابه زاویه adb خواهد بود.
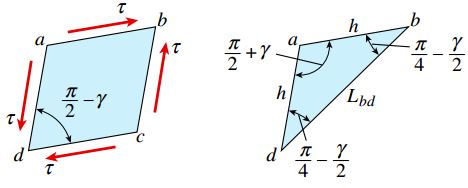
با توجه به موارد بالا، زاویه dab با π/2+γ برابر بوده و رابطه زیر بین اضلاع المان مثلثی برقرار است:
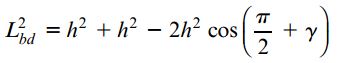
با جایگذاری رابطه Lbd در معادله بالا و سادهسازی طرفین معادله، خواهیم داشت:
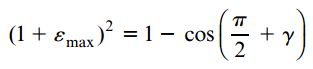
اگر عبارت سمت چپ معادله بالا را باز کنیم و با توجه به قواعد مثلثاتی، (cos(π/2+γ را برابر با sinγ- قرار دهیم:
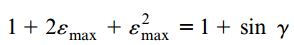
از آنجایی که کرنشهای εmax و γ بسیار کوچک هستند، میتوان از عبارت ε2)max) صرف نظر کرد و γ را به جای sinγ قرار داد. به این ترتیب، معادله بالا به رابطه زیر تبدیل خواهد شد:
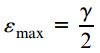
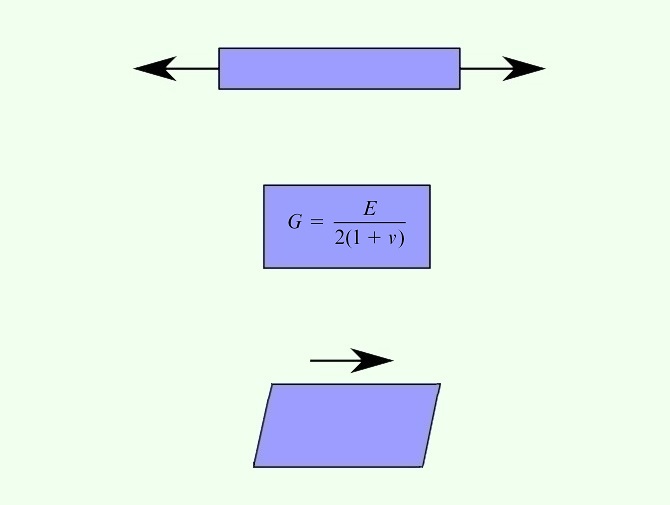
این رابطه، یکی از روابط به دست آمده در مبحث «تعیین مؤلفههای تنش و کرنش در بارگذاری پیچشی» است. بر اساس روابط به دست آمده در این مبحث میتوانیم از τ(1+ν)/E به جای εmax و بر اساس قانون هوک در مواد تحت برش میتوانیم از τ/G به جای کرنش برشی γ در رابطه بالا استفاده کنیم. با اعمال این جایگذاریها خواهیم داشت:
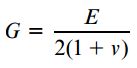
این فرآیند به ما نشان میدهد که کمیتهای G ،E و ν (نسبت پواسون) به عنوان خواص مستقل مواد الاستیک خطی به شمار نمیروند. به این ترتیب، با مشخص بودن دو مورد از این کمیتها میتوان کمیت سوم را نیز محاسبه کرد.
^^













با سلام خیلی عالی بود دست شما درد نکند خدا عوضت بدهد البته اگر برای جنابعالی امکان دارد میشه در مورد نمودار fld-سطح تسلیم و نمودار strain hardening که در autoform استفاده می شود هم به زبان ساده ایی توضیح بفرمایید که مثلا چرا در فلان منطقه ورق فقط برش خالص اتفاق می افتد یا در فلان منطقه ورق فقط کشش خالص اتفاق می افتد چرا تنش بعضی جاها در کشش ورق سه بعدی است بعضی جاها دوبعدی است و بعضی جاها تغییر ضخامت داریم و بعضی جاها نداریم ممنون میشم