پیچش و تغییر شکل های ناشی از آن – به زبان ساده

در مبحث «پیچش»، به معرفی این مفهوم فیزیکی و مبانی مرتبط با آن پرداختیم. در این مقاله، می‌خواهیم تغییر شکل‌های سطح خارجی و مقاطع داخلی میله‌های منشوری در شرایط پیچش خالص را مورد ارزیابی قرار دهیم.

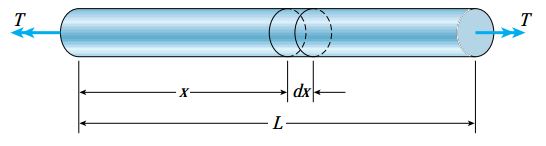
شکل زیر، یک میله منشوری با سطح مقطع دایره‌ای شکل را نمایش می‌دهد. هر دو انتهای این میله توسط گشتاورهای T تحت پیچش قرار گرفته‌اند. به دلیل یکسان بودن مقاطع عرضی در راستای محور طولی و برابر بودن میزان گشتاور داخلی T در آن‌ها، میله تحت «پیچش خالص» (Pure Torsion) قرار دارد. در این شرایط می‌توان اثبات کرد که با چرخش میله حول محور طولی، شکل مقاطع عرضی تغییر نمی‌کند. به عبارت دیگر، تمام مقاطع عرضی به صورت دایره و مسطح و همچنین تمام خطوط شعاعی به صورت مستقیم باقی می‌مانند. علاوه بر این، اگر زاویه چرخش بین دو انتهای میله کوچک باشد، طول و شعاع آن نیز تغییر نخواهند کرد.

برای درک بهتر تغییر شکل به وجود آمده در میله، انتهای سمت چپ آن را ثابت در نظر بگیرید (شکل بالا). با اعمال گشتاور پیچشی T، انتهای سمت راست میله به اندازه زاویه φ نسبت به انتهای ثابتِ آن دوران می‌کند. این زاویه با عنوان «زاویه پیچش» (Angle of Twist) یا «زاویه دوران» (Angle of Rotation) شناخته می‌شود.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

در اثر به وجود آمدن این دوران، خط مستقیم pq بر روی سطح میله به خط مارپیچی ’pq تبدیل خواهد شد. در واقع، محل قرارگیری نقطه q پس از چرخش سطح مقطع انتهایی میله تحت زاویه φ بر روی نقطه ‘q قرار خواهد داشت (شکل زیر).

زاویه پیچش در امتداد محور میله تغییر می‌کند. مقدار این زاویه در مقاطع میانی با (φ(x نمایش داده می‌شود. این مقدار در انتهای چپ میله برابر با صفر و در انتهای راست آن برابر با φ است. اگر تمام مقاطع عرضی دارای شعاع برابر بوده و تحت گشتاور یکسان (پیچش خالص) قرار داشته باشند، زاویه (φ(x در امتداد میله به صورت خطی تغییر می‌کند.

کرنش‌های برشی بر روی سطح خارجی میله

میله زیر و المانی از آن را در نظر بگیرید. این المان بین دو سطح مقطع با فاصله dx از یکدیگر قرار دارد. بر روی سطح خارجی المان، المان کوچک abcd را مشخص می‌کنیم. اضلاع ab و cd با محور طولی میله موازی هستند.

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

در حین اعمال پیچش، سطح مقطع سمت راست به اندازه زاویه کوچک dφ نسبت به سطح مقطع سمت چپ دوران می‌کند. به این ترتیب، نقاط b و c به سمت نقاط ‘b و ‘c جابجا می‌شوند. در حین دوران المان، تغییری در طول اضلاع المان کوچک رخ نمی‌دهد.

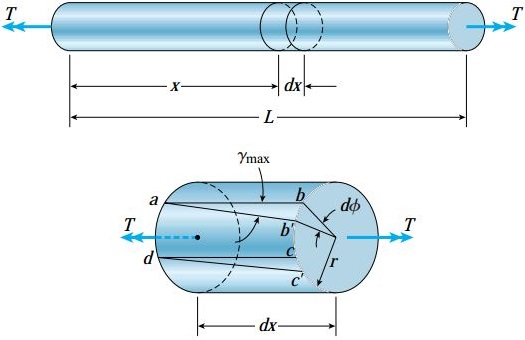
پس از اعمال پیچش، زوایای گوشه‌های المان ab’c’d تغییر می‌کنند و دیگر برابر با 90 درجه نخواهند بود. با توجه به ایجاد کرنش برشی و عدم وجود کرنش‌های نرمال، این المان تحت برش خالص قرار خواهد داشت. مقدار کرنش برشی در سطح خارجی میله (γ_max) با میزان کاهش زاویه در نقطه a (کاهش زاویه گوشه bad) برابر است. با توجه به شکل بالا، میزان کاهش این زاویه از رابطه زیر به دست می‌آید:

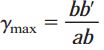
γ_max: کرنش برشی بر حسب رادیان؛ b’b: میزان جابجایی نقطه b؛ و ab: طول المان (dx)

با در نظر گرفتن r به عنوان شعاع میله، میزان جابجایی نقطه b (فاصله b’b) با استفاده از رابطه rdφ قابل محاسبه خواهد بود (dφ برحسب رادیان بیان می‌شود). بنابراین:

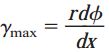
این معادله برای محاسبه کرنش برشی بر روی سطح خارجی میله، با توجه به زاویه پیچش مورد استفاده قرار می‌گیرد. کمیت dφ/dx، نرخ تغییرات زاویه پیچش φ نسبت به فاصله x بر روی محور میله است. این کمیت با علامت θ نمایش داده شده و با عنوان «نرخ پیچش» (Rate of Twist) یا زاویه پیچش بر واحد طول شناخته می‌شود:

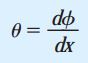
با استفاده از این مفهوم می‌توانیم معادله کرنش برشی در سطح خارجی میله را به صورت زیر بازنویسی کنیم:

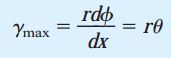
برای به دست آوردن معادلات θ و γ_max، میله را تحت پیچش خالص در نظر گرفتیم. با این وجود، هر دو معادله مذکور برای شرایط کلی‌تر پیچش نیز قابل استفاده هستند. به عنوان مثال، اگر نرخ پیچش θ ثابت نباشد و مقدار آن نسبت به فاصله x در امتداد محور میله تغییر کند نیز می‌توانیم معادلات بالا را مورد استفاده قرار دهیم. در حالت خاص پیچش خالص، نرخ پیچش با تقسیم زاویه پیچش کل (φ) بر طول میله (L) برابر است:

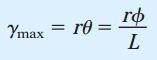
این معادله را می‌توان از طریق روابط هندسی شکل زیر نیز به دست آورد. γ_max، زاویه بین خطوط pq و ’pq (زاویه گوشه ’qpq) را نمایش می‌دهد. بنابراین، γ_maxL با فاصله q’q در انتهای میله برابر خواهد بود. به دلیل برابر بودن ’qq با rφ، به رابطه rφ=γ_maxL می‌رسیم. این رابطه با معادله بالا مطابقت دارد.

کرنش‌های برشی درون میله

کرنش‌های برشی درون میله از طریق روشی مشابه با روش ارائه شده برای تعیین کرنش‌های برشی بر روی سطح به دست می‌آیند.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

به دلیل مستقیم ماندن شعاع مقاطع عرضی و عدم انحراف آن‌ها در حین پیچش، شرایط در نظر گرفته شده برای المان سطحی abcd، برای یک المان واقع بر روی سطح یک استوانه داخلی با شعاع ρ نیز صادق خواهد بود (شکل زیر).

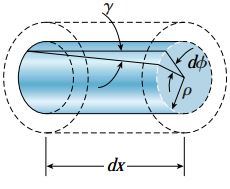
به این ترتیب، این المان داخلی نیز تحت برش خالص قرار خواهد داشت و کرنش‌های برشی مربوط به آن از طریق رابطه زیر محاسبه خواهند شد:

با توجه به این معادله، کرنش‌های برشی درون یک میله دایره‌ای شکل به فاصله شعاعی نقطه مورد بررسی تا مرکز میله بستگی دارند. در مرکز میله، مقدار کرنش‌های برشی به صفر و بر روی سطح خارجی، این کرنش به مقدار حداکثری γ_max می‌رسد.

لوله‌های دایره‌ای شکل

با بررسی مطالب ارائه شده در بخش‌های قبلی می‌توان دریافت که معادلات قبلی برای لوله‌های دایره‌ای نیز قابل استفاده هستند. شکل زیر، نحوه تغییر خطی کرنش‌های برشی بین مقدار ماکسیمم در سطح خارجی و مقدار مینیمم در سطح داخلی یک لوله دایره‌ای شکل را نمایش می‌دهد.

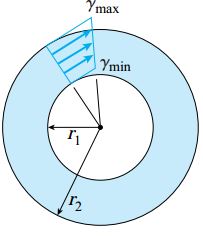
معادلات مربوط به این حالت به صورت زیر نوشته می‌شوند:

r₁: شعاع داخلی لوله؛ r₂: شعاع خارجی لوله

معادلات ارائه شده برای لوله‌های دایره‌ای شکل بر اساس مفاهیم هندسی به دست می‌آیند و به خواص مکانیکی ماده بستگی ندارند. به همین دلیل، این معادلات برای هر نوع ماده‌ای از قبیل خطی یا غیر خطی و الاستیک یا غیر الاستیک قابل استفاده هستند. با این وجود، به خاطر داشته باشید که روابط ارائه شده در این مقاله برای میله‌هایی با زوایای پیچش و کرنش‌های کوچک کاربرد دارند.

^^