مدار مرتبه اول RC – از صفر تا صد (+ دانلود فیلم آموزش رایگان)

در آموزش‌های پیشین مجله فرادرس، اجزای پسیو (مقاومت، سلف و خازن) و برخی از اجزای اکتیو (مانند تقویت‌کننده‌ها) مدار را معرفی کردیم. در این آموزش، مدارهایی را معرفی خواهیم کرد که از ترکیب دوتایی عناصر پسیو ساخته می‌شوند. این مدارها، مدار شامل مقاومت و خازن (مدار RC) و مدار متشکل از مقاومت و سلف (مدار RL) هستند. در این آموزش، مدار مرتبه اول RC را با جزئیات بررسی خواهیم کرد.

مدار RC بدون منبع

یک مدار RC را بدون منبع می‌گوییم اگر منبع dc آن، به‌طور ناگهانی قطع شود.

با قطع منبع، انرژی ذخیره شده قبلی در مدار تخلیه می‌شود.

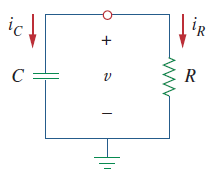
ترکیب سری یک مقاومت و یک خازن را در نظر بگیرید که خازن از قبل شارژ شده است (شکل 1). هدف، تعیین پاسخ مدار است که به دلایل آموزشی، فرض می‌کنیم ولتاژ $$v(t)$$‌ خازن باشد. از آن‌جایی که خازن از قبل شارژ شده است، می‌توان فرض کرد، در زمان $$t=0$$ دارای ولتاژ اولیه زیر است:

که انرژی متناظر با این ولتاژ، برابر است با

با اعمال KCL در گره بالای مدار شکل ۱، داریم:

که در آن، $$i_C=Cdv/dt$$ و $$i_R=v/R$$ هستند. بنابراین:

یا

رابطه بالا، یک معادله دیفرانسیل مرتبه اول است، زیرا تنها مشتق اول $$v$$ در آن وجود دارد. برای حل معادله بالا، آن را به‌صورت زیر بازنویسی می‌کنیم:

اگر از دو طرف معادله بالا انتگرال بگیریم، داریم:

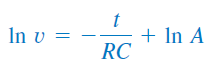
که در آن، $$A$$ ثابت انتگرال‌گیری است. بنابراین،

اگر دو طرف رابطه بالا را به توان $$e$$ برسانیم، خواهیم داشت:

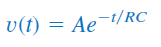
برای تعیین $$A$$ می‌توانیم از شرایط اولیه $$v(0)=A=V_0$$ کمک بگیریم. در نتیجه، پاسخ مدار برابر است با

عبارت بالا نشان می‌دهد پاسخ ولتاژ مدار RC، یک تابع نزولی نمایی از ولتاژ اولیه است. از آن‌جایی که پاسخ به انرژی ذخیره شده و مشخصات فیزیکی مدار وابسته است و به منابع ولتاژ یا جریان خارجی بستگی ندارد، آن را پاسخ طبیعی (Natural response) مدار می‌نامند. به عبارت دیگر، پاسخ طبیعی یک مدار، رفتار (ولتاژ و جریان) آن مدار بدون هیچ منبع تحریک خارجی است.

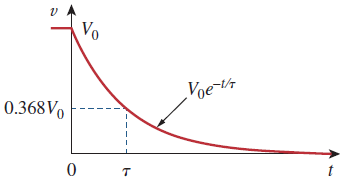
پاسخ طبیعی در شکل ۲ نشان داده شده است. توجه کنید که در $$t=0$$، همان شرایط اولیه (۱) را داریم. با افزایش $$t$$، ولتاژ به صفر کاهش پیدا می‌کند. سرعت کاهش ولتاژ را با ثابت زمانی (Time constant) یا $$\tau$$ نشان می‌دهند. به عبارت بهتر، ثابت زمانی یک مدار، زمان مورد نیاز برای آن است که پاسخ به $$1/e$$ یا 36.8 درصد مقدار اولیه‌اش کاهش پیدا کند.

بنابراین، رابطه (۷) را در $$t=\tau$$ به‌صورت زیر می‌نویسیم:

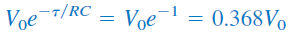
یا

اگر رابطه (۷) را برحسب ثابت زمانی بنویسیم، داریم:

ثابت زمانی را می‌توان از دیدگاه دیگری نیز بررسی کرد. اگر مشتق $$v(t)$$ معادله (۷) را در $$t=0$$ حساب کنیم، داریم:

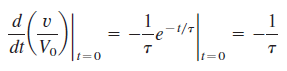
بنابراین، می‌توان گفت ثابت زمانی نرخ کاهش اولیه یا مدت زمانی است که طول می‌کشد $$v/V_0$$ از مقدار واحد (یک) به صفر برسد (با این فرض که نرخ کاهش ثابت باشد). دیدگاه شیب اولیه نسبت به ثابت زمانی، اغلب در آزمایشگاه و برای یافتن $$\tau$$ به‌صورت گرافیکی از روی پاسخ نمایش داده شده روی اسیلوسکوپ استفاده می‌شود (شکل ۳). اگر خط مماس بر پاسخ را در شرایط اولیه رسم کنیم، محور زمان را در $$t=\tau$$ قطع می‌کند.

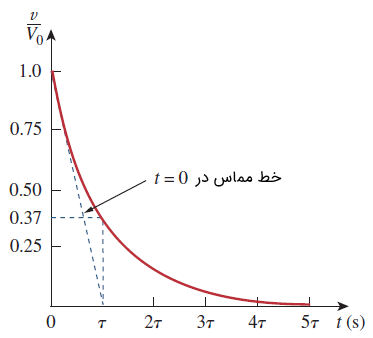
با استفاده از یک ماشین حساب، به‌سادگی می‌توان مقادیر $$v(t)/V$$ را محاسبه کرد که در جدول زیر آورده شده است.

همان‌گونه که از این جدول مشخص است، ولتاژ $$v(t)$$ پس از پنج ثابت زمانی ($$5\tau$$) به کم‌تر از یک درصد $$V_0$$‌می‌رسد. بنابراین، معمولاً فرض می‌کنیم بعد از پنج ثابت زمانی، خازن کاملاً شارژ (یا دشارژ) می‌شود. به عبارت دیگر، اگر تغییرات خاصی رخ ندهد، $$5 \tau$$‌ طول می‌کشد که مدار به حالت نهایی یا حالت ماندگار برسد. گفتنی است که بعد از گذشت هر ثابت زمانی (و بدون توجه به مقدار $$t$$)، ولتاژ به 36.8 درصد مقدار قبلی می‌رسد؛ یعنی $$v(t+\tau)=v(t)/e=0.368v(t)$$.

رابطه (۸) نشان می‌دهد هرچه ثابت زمانی کوچک‌تر باشد، ولتاژ سریع‌تر کاهش می‌یابد و پاسخ سریع‌تر خواهد بود. این موضوع، در شکل ۴ نشان داده شده است. سرعت پاسخ هر اندازه که باشد، مدار بعد از گذشت ۵ ثابت زمانی به حالت ماندگار می‌رسد.

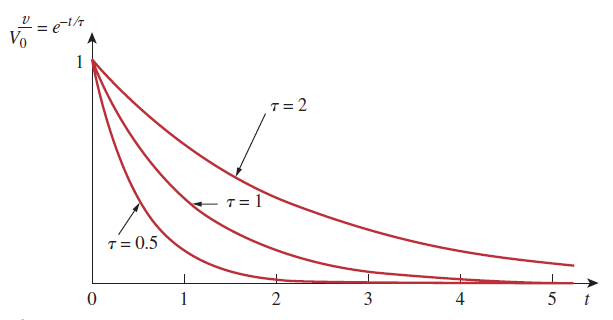
با داشتن ولتاژ $$v(t)$$ از رابطه (۹)، می‌توان جریان $$i_R(t)$$‌ را به‌صورت زیر نوشت:

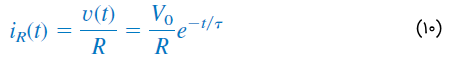
توانی که در مقاومت تلف می‌شود، از رابطه زیر به‌دست می‌آید:

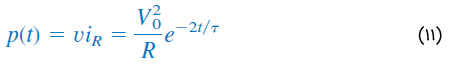
انرژی جذب شده مقاومت در زمان $$t$$ نیز برابر است با:

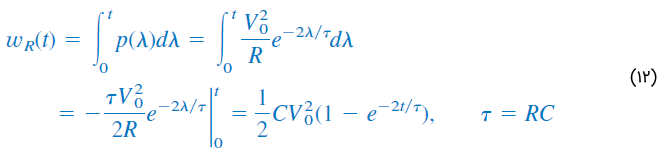
اگر $$t \to \infty$$، آن‌گاه $$w_R(\infty) \to \frac{1}{2} CV_0^2$$ را داریم که برابر با همان مقدار انرژی ذخیره شده اولیه در خازن ($$w_C(0)$$) است.

به‌عنوان نتیجه‌گیری، می‌توان گفت دو پارامتر مهم برای مدار مرتبه اول RC بدون منبع وجود دارد که ولتاژ اولیه خازن و ثابت زمانی هستند. با استفاده از این دو مورد، می‌توان پاسخ مدار را در قالب ولتاژ خازن $$v_C(t)=v(t)=v(0)e^{-t/\tau}$$ به‌دست آورد. پس از آنکه ولتاژ خازن به‌دست آمد، سایر متغیرها (جریان خازن $$i_C$$، ولتاژ مقاومت $$v_R$$ و جریان مقاومت $$i_R$$) را می‌توان تعیین کرد.

در ثابت زمانی $$\tau = RC$$، معمولاً $$R$$‌ مقاومت معادل تونن از دو سر خازن است. خازن نیز، خازن معادل مدار است.

توابع تکین

قبل از اینکه وارد بحث درباره نوع دیگر مدارهای مرتبه اول RC شویم، لازم است چند مفهوم ریاضی را بیان کنیم که موجب تسهیل درک تحلیل گذارا می‌شوند. آشنایی اولیه با توابع تکین (Singularity functions) ما را در تحلیل پاسخ مدارهای مرتبه اول به اعمال ناگهانی منابع ولتاژ یا جریان dc کمک خواهد کرد.

توابع تکین که توابع سوئیچینگ یا کلیدزنی نیز نامیده می‌شوند، در تحلیل مدار بسیار مفید خواهند بود. این توابع، تقریب‌های مناسبی برای سیگنال‌های سوئیچینگ هستند که به مدار اعمال می‌شوند. توابع تکین، برای توصیف مناسب و فشرده برخی پدیده‌های مدار، خصوصاً پاسخ مدارهای RC و RL مفید هستند. بنا بر تعریف، توابع تکین، توابعی ناپیوسته هستند یا مشتق‌های ناپیوسته دارند. توابع تکین پرکاربرد که در تحلیل مدارهای الکتریکی مورد استفاده قرار می‌گیرند، پله واحد، ضربه واحد و شیب واحد هستند.

تابع پله واحد

تابع پله واحد $$u(t)$$ برای مقادیر منفی $$t$$، صفر و برای مقادیر مثبت $$t$$ برابر با ۱ است.

به بیان ریاضی:

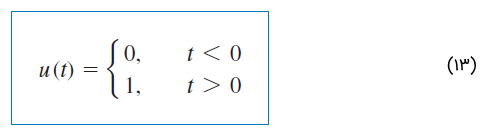
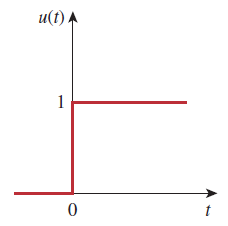
تابع پله واحد در $$t=0$$ که تغییر ناگهانی از 0 به 1 رخ می‌دهد، تعریف نشده است. این تابع، مانند سایر توابع ریاضیاتی مثل سینوس و کسینوس بدون بُعد است. شکل ۵، تابع پله واحد را نشان می‌دهد. اگر تغییر ناگهانی به جای $$t=0$$ در $$t=t_0$$‌ ($$t>t_0$$) رخ دهد، تابع پله به‌شکل زیر خواهد بود:

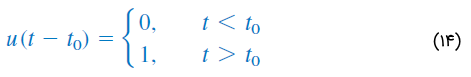
در این حالت می‌گوییم، $$u(t)$$ به‌اندازه $$t_0$$ ثانیه تاخیر یافته است (شکل 6 (الف)).‌ برای به‌دست آوردن رابطه (۱۴) از رابطه (۱۳)، می‌توان به‌سادگی $$t$$ را با $$t-t_0$$ جایگزین کرد. اگر تغییر ناگهانی در $$t=-t_0$$ اتفاق افتد، تابع پله را می‌توان به‌صورت زیر نوشت:

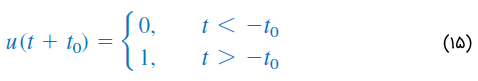
بدین ترتیب، مطابق شکل 6 (ب)، $$u(t)$$‌ به‌اندازه $$t_0$$‌ ثانیه جلو می‌افتد.

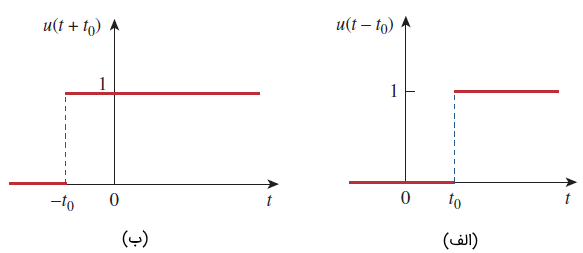
از تابع پله برای نشان دادن تغییر ناگهانی در ولتاژ یا جریان استفاده می‌کنیم. این کار مخصوصاً در سیستم‌های کنترل و کامپیوترهای دیجیتال کاربرد دارد. برای مثال، ولتاژِ

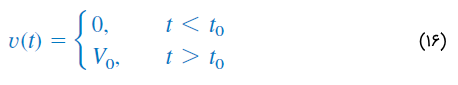
را می‌توان با تابع پله واحد زیر نشان داد:

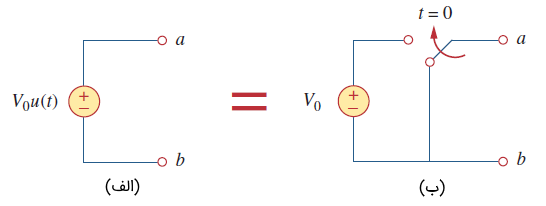
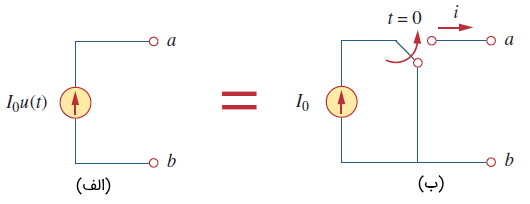
اگر $$t_0=0$$ را در نظر بگیریم، آن‌گاه $$v(t)$$‌ را می‌توان به‌صورت تابع پله $$V_0 u(t)$$‌ نوشت. منبع ولتاژ $$V_0u(t)$$ در شکل ۷ (الف) و مدار معادل آن، در شکل ۷ (ب) نشان داده شده است. از شکل ۷ (ب) مشخص است که ترمینال‌های a-b در $$t<0$$ اتصال کوتاه هستند ($$v=0$$) و برای $$t>0$$، ولتاژ برابر $$v=V_0$$ است. به طریق مشابه، منبع جریان $$I_0 u(t)$$ و مدار معادل آن، در شکل 8 (الف) و ۸ (ب) نشان داده شده‌اند. همان‌طور که می‌بینیم، برای $$t<0$$، منبع، مدار باز است ($$i=0$$) و در $$t>0$$ جریان آن برابر با $$i=I_0$$ خواهد بود.

تابع ضربه واحد

مشتق تابع پله واحد $$u(t)$$، تابع ضربه واحد $$\delta (t)$$ است که به‌صورت زیر نوشته می‌شود:

تابع ضربه واحد را، تابع دلتا نیز می‌نامند. شکل ۹ این تابع را نشان می‌دهد. تابع ضربه واحد $$\delta (t)$$، جز در $$t=0$$ تعریف نشده است.

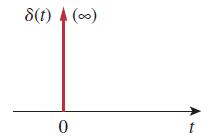
جریان‌ها و ولتاژهای ضربه‌ای مدار، بر اثر کلیدزنی یا منابع ضربه‌ای ایجاد می‌شوند. اگرچه تابع ضربه واحد از نظر فیزیکی قابل پیاده‌سازی نیست (مانند منابع ایده‌آل، مقاومت‌های ایده‌آل و غیره)، اما ابزار ریاضی بسیار مفیدی است. تابع ضربه را می‌توان به‌عنوان یک شوک در نظر گرفت یا به‌عنوان یک پالس بسیار کوتاه با مساحت واحد تصور کرد. به زبان ریاضی، می‌توان نوشت:

که در آن، $$t=0^-$$، زمان را اندکی قبل از $$t=0$$‌ و $$t=0^+$$ زمان را اندکی بعد از $$t=0$$‌ نشان می‌دهد. مساحت واحد را به‌عنوان شدت تابع ضربه می‌شناسند. وقتی یک ضربه، شدت بیشتری نسبت به واحد داشته باشد، مساحت آن، برابر با آن شدت است. برای مثال، مساحت تابع ضربه $$10 \delta (t)$$، برابر با 10 است. شکل 10، توابع ضربه $$5\delta (t+2)$$، $$10 \delta (t)$$ و $$-4\delta (t-3)$$ را نشان می‌دهد.

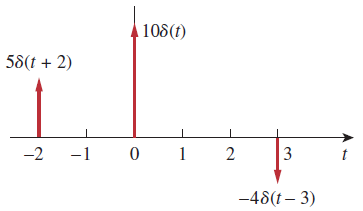
برای آنکه تاثیر تابع ضربه را بر سایر توابع پیدا کنیم، انتگرال زیر را محاسبه می‌کنیم:

که در آن، $$a$$. از آن‌جایی که مقدار $$\delta (t-t_0)$$ جز در $$t=t_0$$ برابر با صفر است، انتگرال‌ده جز در $$t_0$$‌ برابر با صفر است. بنابراین:

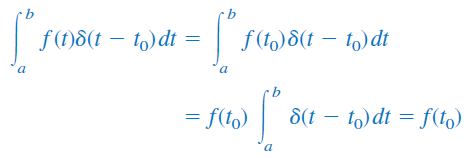
یا

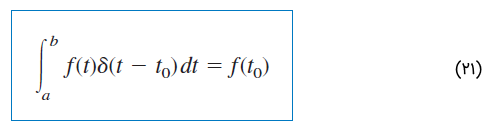
رابطه بالا نشان می‌دهد وقتی از حاصل‌ضرب یک تابع و تابع ضربه، انتگرال بگیریم، مقدار تابع در نقطه‌ای به‌دست می‌آید که ضربه اعمال شده است. این ویژگی تابع ضربه که بسیار هم مفید است، خاصیت نمونه‌برداری (Sampling)‌ یا جابه‌جایی (Shifting) نامیده می‌شود. در حالت خاص، معادله (۲۰) را می‌توان برای $$t_0=0$$‌ به‌صورت زیر نوشت:

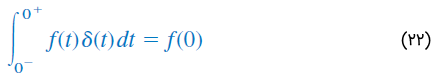
تابع شیب واحد

انتگرال‌گیری از تابع پله واحد $$u(t)$$، تابع شیب واحد $$r(t)$$‌ را نتیجه خواهد داد:

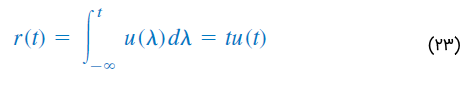
یا

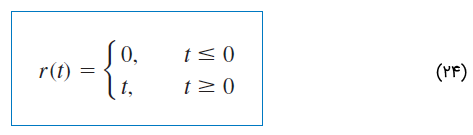
تابع شیب واحد، برای مقادیر $$t$$ منفی، برابر با صفر است و برای $$t$$های مثبت، یک شیب واحد است. شکل 1۱، تابع شیب واحد را نشان می‌دهد. در حالت کلی، یک شیب، تابعی است که با نرخ ثابتی تغییر می‌کند.

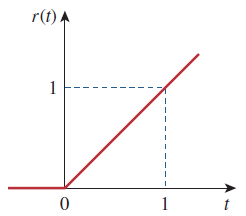
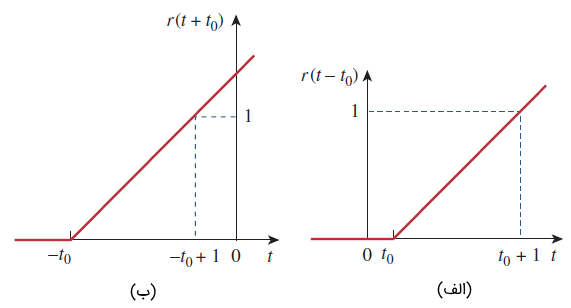
تابع شیب واحد، را می‌توان مطابق شکل 1۲، عقب یا جلو برد. برای یک تابع شیب واحد تاخیریافته، داریم:

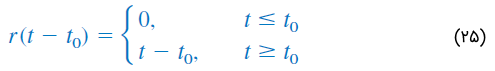
و یک تابع شیب پیش افتاده به‌صورت زیر است:

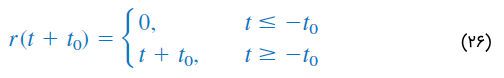
به خاطر داشته باشید سه تابع تکین (ضربه، پله و شیب) را می‌توان با مشتق یا انتگرال به یک‌دیگر مربوط کرد:

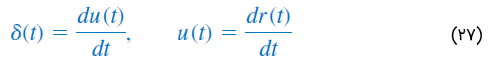
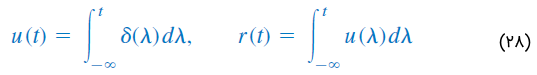
هرچند توابع تکین دیگری نیز وجود دارد، اما ما با این سه تابع سروکار داریم.

پاسخ پله یک مدار RC

وقتی یک منبع dc به‌طور ناگهانی به مدار RC‌ اعمال شود، منبع ولتاژ یا جریان را می‌توان با یک تابع پله مدل کرد که پاسخ آن، به‌عنوان پاسخ پله شناخته می‌شود.

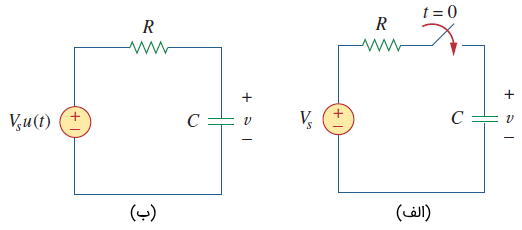
مدار RC شکل 1۳ (الف) را در نظر بگیرید که می‌توان آن را با مدار شکل 13 (ب) جایگزین کرد. در این شکل، $$V_s$$ یک منبع ولتاژ dc ثابت است. در این‌جا نیز ولتاژ خازن را به‌عنوان پاسخ مدار در نظر می‌گیریم. فرض می‌کنیم، مقدار اولیه ولتاژ خازن $$V_0$$ است. از آن‌جایی که ولتاژ خازن به‌طور ناگهانی تغییر نمی‌کند، داریم:

که $$v(0^-)$$، ولتاژ خازن قبل از کلیدزنی و $$v(0^+)$$، ولتاژ خازن دقیقاً بعد از کلیدزنی است. با اعمال KCL، داریم:

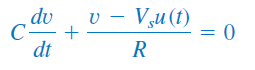
یا

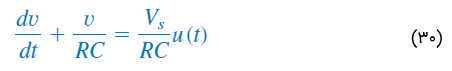
که در آن، $$v$$ ولتاژ خازن است. برای $$t>0$$، رابطه (30) به‌صورت زیر در خواهد آمد:

با کمی جابه‌جایی، داریم:

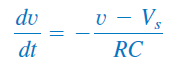
یا

اگر از دو طرف رابطه بالا با توجه به شرایط اولیه انتگرال بگیریم، نتیجه زیر حاصل می‌شود:

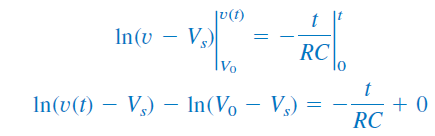
یا

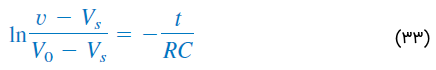
اگر دو طرف رابطه بالا را به توان $$e$$‌ برسانیم، داریم:

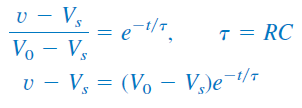
یا

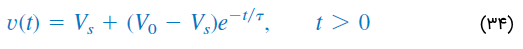
بنابراین،

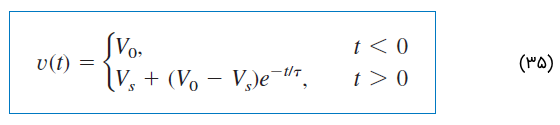
عبارت بالا، به‌عنوان پاسخ کامل (Complete response) مدار RC‌ با اعمال ناگهانی یک منبع ولتاژ dc و با فرض شارژ اولیه خازن نامیده می‌شود. دلیل نام «کامل» را اندکی بعد، متوجه خواهید شد. با فرض $$V_s>V_0$$، شکل 1۴، نمودار $$v(t)$$‌ را نشان می‌دهد.

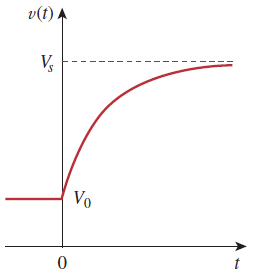
اگر فرض کنیم خازن در حالت اولیه شارژ نشده باشد، مقدار $$V_0=0$$ را در معادله (35) قرار می‌دهیم:

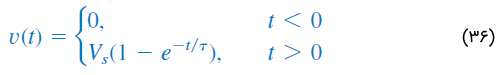
که می‌توان آن را به‌صورت زیر نوشت:

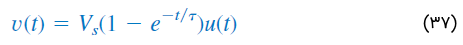
معادله بالا، پاسخ مدار در حالتی است که خازن از قبل شارژ نشده باشد. جریان خازن را می‌توان از رابطه (36) و با استفاده از $$i(t)=Cdv/dt$$ نوشت:

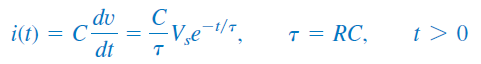
یا

شکل 15، نمودار ولتاژ و جریان خازن را نشان می‌دهد.

جدای از عملیاتی که برای به‌دست آوردن ولتاژ خازن انجام شد، یک روش نظام‌مند یا به تعبیر بهتر، میان‌بُر برای یافتن پاسخ پله یک مدار RC‌ یا RL وجود دارد. دوباره معادله (۳۴) را در نظر بگیرید که عمومی‌تر از رابطه (۳۷) است. مشخص است که $$v(t)$$ دو بخش دارد. دو راه برای تفکیک این دو بخش وجود دارد. راه اول، جدا کردن پاسخ به دو بخش «پاسخ طبیعی و پاسخ اجباری» و راه دوم، جدا کردن به دو بخش «پاسخ گذرا و پاسخ حالت ماندگار» است. از روش اول شروع می‌کنیم. پاسخ کامل یک مدار را می‌توان به صورت زیر بیان کرد:

یا

که

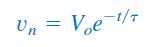
و

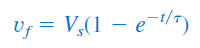
در بخش نخست این آموزش، با پاسخ طبیعی $$v_n$$ مدار آشنا شدیم. $$v_f$$، به‌عنوان پاسخ اجباری (Forced response) شناخته می‌شود، زیرا وقتی ایجاد می‌شود که یک نیرو (force) خارجی (در این بحث، منبع ولتاژ) به مدار اعمال شود.

راه دیگر بیان پاسخ کامل، جدا کردن آن به دو بخش موقت و دائمی است:

یا

که

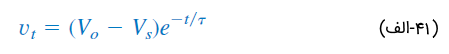
و

پاسخ گذرای $$v_t$$، موقتی است و بخشی از پاسخ است که با میل کردن زمان به بی‌نهایت، مقدار آن به صفر می‌رسد. پاسخ حالت ماندگار $$v_{ss}$$، آن بخش از پاسخ است که پس از از بین رفتن پاسخ گذرا، باقی می‌ماند.

روش تفکیک نخست برای پاسخ کامل، بر اساس منبع پاسخ است، درحالی که روش دوم، مبتنی بر دوام پاسخ‌ها است. در شرایط معین، پاسخ طبیعی و گذرا مشابه هستند. در نتیجه می‌توان گفتن که پاسخ اجباری و حالت ماندگار نیز برابر خواهند بود.

از هر دیدگاهی که به پاسخ کامل نگاه کنیم، می‌توان رابطه (۳۴) را به‌صورت زیر نوشت:

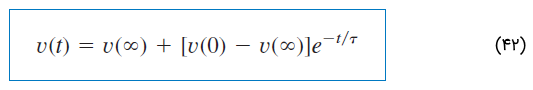
که در آن، $$v(0)$$، ولتاژ اولیه در $$t=0^+$$ و $$v(\infty)$$، مقدار نهایی یا حالت ماندگار است. بنابراین، برای یافتن پاسخ پله یک مدار RC، به سه پارامتر نیاز داریم:

1. ولتاژ‌ اولیه خازن $$v(0)$$
2. ولتاژ نهایی خازن $$v(\infty)$$
3. ثابت زمانی $$\tau$$.

مورد ۱ را می‌توان در زمان $$t<0$$ برای مدار به‌دست آورد. موارد 2 و ۳ نیز در $$t>0$$ به‌دست می‌آیند. با محاسبه این موارد، می‌توان پاسخ را از رابطه (۴۲) به‌دست آورد.

توجه کنید اگر کلید به‌جای $$t=0$$ در لحظه $$t=t_0$$ سوئیچ شود، یک تاخیر زمانی در رابطه (42) ایجاد خواهد شد:

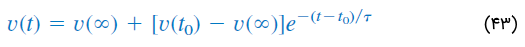
که در آن، $$v(t_0)$$، مقدار اولیه در $$t=t_0^+$$ است. روابط (42) و (43)، فقط در مورد پاسخ پله کاربرد دارند، یعنی وقتی تحریک ورودی، ثابت است.

معرفی فیلم آموزش فیزیک یازدهم

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک یازدهم کرده است. این مجموعه آموزشی مباحث فیزیک یازدهم را پوشش می‌دهد. در این مجموعه ابتدا به آموزش الکتریسیته ساکن، میدان الکتریکی، خطوط میدان الکتریکی، انرژی پتانسیل الکتریکی، خازن و دی الکتریک پرداخته می‌شود و در انتهای بخش اول نمونه تست‌های کنکور سراسری مورد بررسی قرار می‌گیرند.

در درس دوم این مجموعه الکتریسیته جاری مورد بحث قرار می‌گیرد و آموزش موضوعاتی نظیر جریان الکتریکی، قانون اهم، مقاومت الکتریکی، باتری و توان آن نیز پوشش داده می‌شوند. حل تست‌های کنکور سراسری مربوط به این مباحث پایان بخش این قسمت از آموزش‌ خواهد بود.

در ادامه و در درس سوم آموزش مطالب مربوط به مغناطیس‌ها ارائه می‌شود که شامل سرفصل‌هایی مانند قطب‌های مغناطیسی، میدان مغناطیسی، نیروی وارد بر سیم حامل جریان باردار و انواع مواد مغناطیسی و ویژگی‌های آن‌ها است. تست‌های کنکور سراسری مربوط به این مبحث نیز در انتهای آن مورد بررسی قرار گرفته‌اند.

در انتها و در درس چهارم القای الکترومغناطیسی و جریان متناوب مورد بررسی قرار می‌گیرد. محاسبه نیروی محرکه القایی، قانون القای فارادی و موضوعات مربوط به القاگرها از مهم‌ترین مباحث مربوط به این درس هستند. لینک این آموزش در ادامه آورده شده است.

• برای مشاهده فیلم آموزش فیزیک یازدهم + اینجا کلیک کنید.

معرفی فیلم آموزش فیزیک ۲ دانشگاه

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم  آموزش فیزیک ۲ دانشگاه برای دانشجویان علوم پایه و فنی و مهندسی کرده است. این مجموعه آموزشی از شانزده درس تشکیل شده و برای دانشجویان رشته علوم پایه و فنی مهندسی مفید است. پیش‌نیاز این درس آموزش فیزیک پایه ۱، ریاضی ۱ و معادلات دیفرانسیل است.

درس اول و دوم این مجموعه به ترتیب به بار الکتریکی و میدان‌های الکتریکی اختصاص دارد. درس سوم و چهارم در مورد قانون گاوس صحبت خواهد کرد و درس پنجم به مفهوم پتانسیل الکتریکی می‌پردازد. درس ششم، هفتم و هشتم مربوط به مفاهیم ظرفیت، جریان و مقاومت و مدار‌ها است و درس نهم به معرفی مفهوم میدان‌های الکترومغناطیسی می‌پردازد. در درس دهم مفهوم میدان‌های مغناطیسی حاصل از جریان‌ها معرفی می‌شود و در درس یازدهم و دوازدهم القا و خودالقایی آموزش داده می‌شود. درس سیزدهم و چهاردهم این مجموعه آموزشی به موضوع نوسان‌های الکترومغناطیسی و جریان های متناوب اختصاص دارد و درس پانزدهم به معرفی معادلات ماکسول می‌پردازد. در نهایت در درس شانزدهم امواج الکترومغناطیس آموزش داده می‌شود.

• برای مشاهده آموزش فیزیک ۲ دانشگاه + اینجا کلیک کنید.

در صورتی که مباحث بیان شده برای شما مفید بوده و می‌خواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد می‌کنیم به آموزش‌های زیر مراجعه کنید:

• دو قطبی در مدارهای الکتریکی — به زبان ساده
• تزویج در مدارهای الکتریکی — مفاهیم اصلی

^^