تبدیل رادان یا Radon Transform – تعاریف و مفاهیم
در این مطلب با تبدیل رادان یا Radon Transform پرداخته شده است.
تبدیل رادن
در ریاضیات، تبدیل رادن (Radon transform) در دو بعد، که نام خود را از ریاضیدان ژوهان رادن گرفته است، تبدیلی انتگرالی است که برابر با انتگرال تابع بر روی خطوط مستقیم میباشد. این تبدیل در سال 1917 توسط رادن معرفی شد. وی فرمولی را نیز برای معکوس تبدیل ارائه نمود. رادن همچنین فرمولهایی را برای تبدیل در سه بُعد پیشنهاد کرده است که در آن انتگرال بر روی صفحات گرفته میشود. این فرمولها بعدتر برای فضای اقلیدسی ابعاد بالاتر، تعمیم داده شدند.
تبدیل رادن به صورت گستردهای در توموگرافی یا برشنگاری (تولید تصویر از پروجکشن دادهی مرتبط با اسکنهای cross-sectional از یک شیء) کاربرد دارد. اگر تابع f نشانگر یک تراکم ناشناخته باشد، آنگاه تبدیل رادن، دادهی پروجکشن به دست آمده به عنوان خروجی اسکن توموگرافیک را نشان میدهد. بنابراین معکوس تبدیل رادن میتواند برای بازسازی تراکم اصلی از داده پروجکشن به کار رود، و بدین ترتیب پایه ریاضی بازسازی توموگرافیک را که بازسازی تصویر نامیده میشود، تشکیل دهد. دادهی تبدیل رادن، اغلب سینوگرام (sinogram) نامیده میشود زیرا تبدیل رادنِ یک تابع دلتای دیراک، به شکل توزیعی بر روی گراف یک موج سینوسی میباشد. در نتیجه، تبدیل رادنِ تعدادی از اشیاء، ظاهر گرافیکیای همچون چندین موج سینوسی با فاز و دامنه مختلف دارد. تبدیل رادن در سیتی اسکن، اسکنر بارکد، ذرهبینی الکترونی ویروسها و پروتئینها، انعکاس لرزهای و حل معادلات هذلولی دیفرانسیلی با مشتقات پارهای، مفید است.
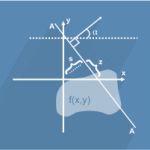
تعریف تبدیل رادان
فرض کنید (ƒ(x) = ƒ(x,y تابع پیوسته کاملا پشتیبانی شده (compactly supported) بر روی R2 باشد. تبدیل رادن، Rƒ، برابر خواهد بود با:
![]()
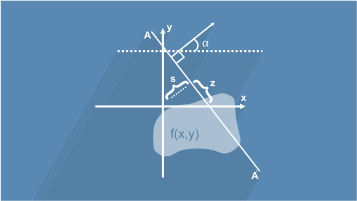
پارامتریزه کردن هر خط مستقیم L با توجه به طول کمان z همواره میتواند به صورت زیر نوشته شود:
![]()
که s فاصله L از مبدا و زاویهای است که بردار نرمال L با محور x میسازد. مقادیر (α,s)میتوانند به عنوان مختصات روی فضای تمام خطوط در R2 در نظر گرفته شوند، و تبدیل رادن میتواند در این مختصات توسط معادله زیر بیان شود:
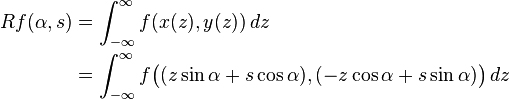
به صورت کلی، در فضای اقلیدسی n-بعدی Rn، تبدیل رادن یک تابع پیوسته کاملا پشتیبانی شده( f) برابر است با تابعی بر روی فضای Σn کل ابرصفحهها در Rn (Rf). این تبدیل برای برای ξ ∈Σn وقتی که انتگرال با توجه به اندازه طبیعی ابرسطح، dσ، گرفته میشود (تعمیم عبارت |dx| از مسئله دو بعدی) بدین ترتیب تعریف میشود:
![]()
توجه کنید که هر عنصر Σn به صورت مکان هندسی راهحلی برای یک معادله توصیف میشود:
![]()
که α ∈ Sn−1 یک بردار واحد است و s ∈ R میباشد. بنابراین، تبدیل رادن n-بعدی میتواند به صورت تابعی بر روی Sn−1×R نوشته شود:
![]()
حال که با مفهوم تبدیل رادان آشنا شدید، ممکن است که مطالب آموزش های زیر از فرادرس برای شما مفید باشد:











