انرژی پتانسیل چیست؟ – به زبان ساده
انرژی پتانسیل یک جسم را میتوان به صورت کلی برابر با اختلاف انرژی آن جسم در یک موقعیت، نسبت به انرژی آن در مکان مرجع معرفی کرد. به صورت کلی، انرژی پتانسیل، شامل انرژی پتانسیل کشسانی، گرانشی و الکتریکی است و این انرژی کاربرد بسیار زیادی در علم فیزیک و مهندسی مکانیک دارد.


این مطلب ابتدا به بررسی مفهوم انرژی پتانسیل و رابطه کلی آن میپردازد و سپس انواع انرژی پتانسیل و روابط حاکم بر آنها را مورد مطالعه قرار میدهد. همچنین در مطالب دیگر وبلاگ فرادرس، کاربرد این انرژی در حل مسائل به کمک «قضیه کار و انرژی» مورد مطالعه قرار میگیرد.
انرژی پتانسیل چیست؟
همانطور که بیان شد، انرژی پتانسیل یک جسم در مکان مشخص، برابر با اختلاف انرژی جسم در آن مکان، نسبت به موقعیت مرجع است. انرژی پتانسیل، عموما به نیروهایی مانند نیروی گرانش و کشسانی فنر مرتبط است. برای مثال، زمانی که یک توپ سنگین در ارتفاع معینی قرار گرفته، انرژی را در خود ذخیره کرده است. این انرژی ذخیره شده در جسم که ناشی از ارتفاع آن است، انرژی پتانسیل نامیده میشود.

به صورت مشابه میتوان بیان کرد که موقعیت یک کمان کشیده شده، میزان انرژی ذخیره شده در آن را تعیین میکند. در واقع، زمانی که کمان در موقعیت ابتدایی خود قرار دارد، یعنی زمانی که کشیده نشده، انرژی نیز در آن ذخیره نشده است و زمانی که موقعیت کمان نسبت به حالت عادی آن تغییر میکند، انرژی در آن ذخیره میشود که این انرژی ذخیره شده را، انرژی پتانسیل مینامند. بنابراین در این مثال نیز میتوان بیان کرد که انرژی پتانسیل، انرژی ذخیره شده در جسم و ناشی از موقعیت آن است.

در شرایط ذکر شده، یک نیروی خارجی، عامل حفظ وضعیت جسم در موقعیتهایی به غیر از موقعیت مرجع آن است. در صورتی که این نیروی خارجی حذف شود، انرژی پتانسیل باعث ایجاد کار در سیستم میشود و سیستم را به موقعیت مرجع باز میگرداند. در واقع حذف نیروهای خارجی در مثالهای ذکر شده، باعث میشود که توپ سنگین به پایین حرکت کند و یا مقدار کشیده شدن کمان کاهش یابد.
اگر کار ناشی از نیروی وارد شده بر جسم، مستقل از مسیر باشد (این شرایط در صورتی ایجاد میشود که نیروی مورد نظر پایستار باشد)، تنها نیاز به محاسبه کار در ابتدا و انتهای مسیر داریم. این نکته، بیان میکند که تابعی به فرم (U(x (این تابع، پتانسیل نامیده میشود) موجود است که در موقعیت ابتدایی یعنی (x(t=t1 و انتهایی یعنی (x(t2 قابل محاسبه است. این دو مقدار برای محاسبه کار تمام مسیرهای دلخواهی استفاده میشود که بین دو حالت ابتدایی و انتهایی وجود دارند. این موضوع با استفاده از رابطه زیر قابل بیان است.
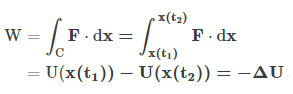
انواع انرژی پتانسیل
انواع مختلفی از انرژی پتانسیل موجود است که هریک به نیروی خاصی مرتبط است. به صورت جزئیتر میتوان بیان کرد که هر نیروی پایستار باعث افزایش انرژی پتانسیل میشود. برای مثال، کار ناشی از نیروی کشسانی را انرژی پتانسیل کشسانی مینامند و کار ناشی از نیروی گرانش، انرژی پتانسیل گرانشی نامیده میشود. همچنین کار ناشی از «نیروی کولن» (Coulomb Force) را به عنوان انرژی پتانسیل الکتریکی معرفی میکنند.
انرژی پتانسیل گرانشی
همانطور که بیان شد، انرژی گرانشی نوعی از انرژی پتانسیل است که در نتیجه نیروی گرانشی ایجاد میشود و مقدار کاری را نشان میدهد که برای غلبه بر نیروی گرانش، هنگام قرار دادن یک جسم در ارتفاع مشخص، مورد نیاز است.
در واقع انرژی پتانسیل گرانشی، انرژی است که در یک جسم به دلیل ارتفاع عمودی آن ذخیره میشود. این انرژی در جسم به دلیل جاذبه میان زمین و جسم، ذخیره میشود. برای مثال آب پشت سد به دلیل ارتفاع خود نسبت به سطح رود پایین دست، انرژی پتانسیل گرانشی دارد و از این انرژی به کمک توربوماشینها، برای تولید برق در نیروگاههای آبی استفاده میشود. این مورد در شکل زیر به تصویر کشیده شده است.

انرژی پتانسیل گرانشی یک توپ بزرگ، به دو عامل وابسته است. عامل اول، جرم این توپ و عامل دوم ارتفاع قرارگیری آن است. در واقع میتوان نمایش داد که میزان انرژی پتانسیل گرانشی یک جسم، ارتباط مستقیمی با جرم آن دارد و هرچه جرم جسم بیشتر باشد انرژی پتانسیل گرانشی آن نیز بیشتر است. علاوه بر موارد ذکر شده، میتوان نشان داد که ارتباط مستقیمی میان انرژی پتانسیل گرانشی یک جسم و ارتفاع آن وجود دارد. بنابراین، هرچه ارتفاع یک جسم بیشتر باشد، انرژی پتانسیل گرانشی آن نیز بیشتر است.
نکته مهم دیگری که باید به آن اشاره کرد این است که، اگر یک جسم در میدان گرانش از یک نقطه به نقطه پایینتر حرکت کند، نیروی گرانش، کار مثبت روی جسم انجام میدهد و انرژی پتانسیل گرانشی به همان اندازه کاهش پیدا میکند.
رابطه انرژی پتانسیل گرانشی برای یک جسم به جرم m که در ارتفاع h از سطح مرجع قرار گرفته، به شکل زیر قابل نمایش است. توجه شود که سطح مرجع، مکانی است که انرژی پتانسیل گرانشی در آن، برابر با صفر فرض میشود.
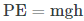
عبارت سمت چپ رابطه بالا، انرژی پتانسیل را نشان میدهد که در این رابطه واحد آن ژول (J) است. m، جرم جسم در واحد کیلوگرم (kg) را نشان میدهد و مقدار h، برابر با فاصله عمودی از سطح مرجع است. شتاب گرانش نیز با نماد g، بیان میشود که مقدار آن در سطح زمین برابر با است. توجه شود که در این رابطه، مقدار شتاب گرانش در نزدیکی زمین، ثابت فرض شده است.
رابطه کلی انرژی پتانسیل گرانشی
نکته مهمی که باید به آن اشاره کرد این است که زمانی که تغییرات ارتفاع زیاد باشد، ثابت فرض کردن مقدار شتاب گرانش (g)، تقریب درستی نخواهد بود. بنابراین در این شرایط، نمیتوان مقدار شتاب گرانش را، ثابت در نظر گرفت. در این حالت باید از رابطه عمومی و تعریف گرانش برای محاسبه انرژی پتانسیل گرانشی بهره گرفته شود.
در قسمت قبل، نشان دادیم که انرژی پتانسیل را میتوان با انتگرالگیری از نیروی پایستار در طول مکان محاسبه کرد. بنابراین در این قسمت نیز برای محاسبه انرژی پتانسیل گرانشی در حالت کلی، از نیروی گرانش انتگرال میگیریم. رابطه نیروی گرانش به شکل زیر نشان داده میشود. این رابطه اولین بار توسط نیوتن بیان شده است.
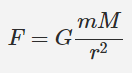
بنابراین انرژی پتانسیل مجموعهای شامل دو جرم m و M که در فاصله r از یکدیگر قرار گرفتند، با استفاده از رابطه زیر قابل محاسبه است.
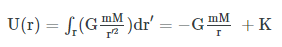
در رابطه بالا، K ثابت انتگرالگیری است. در صورتی که طبق یک قرارداد در تمام مسائل، k را برابر با صفر در نظر بگیریم، حل مسائل بسیار سادهتر خواهد بود. هرچند طبق این قرارداد مقدار U منفی میشود ولی مقدار انرژی پتانسیل برای زمانی که فاصله دو جسم بینهایت است برابر با صفر به دست میآید.
در این روابط G، ثابت گرانش نامیده میشود که مقدار آن با استفاده از رابطه زیر قابل محاسبه است.
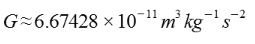
انرژی پتانسیل کشسانی فنر
همانطور که اشاره شد، زمانی که یک فنر از نقطه تعادل خود به مقدار x، فشرده و یا کشیده شود، انرژی پتانسیل در فنر ذخیره میشود که با رها شدن آن، این انرژی پتانسیل، تمایل به بازگشت فنر به حالت اولیه آن دارد. اندازه انرژی پتانسیل کشسانی فنر به طور کلی با استفاده از رابطه زیر محاسبه میشود.
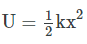
نیروی فنر یک نیروی پایستار است. این نیرو با استفاده از «قانون هوک» (Hooke’s Law) به شکل زیر محاسبه میشود.
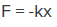
در این رابطه، k ثابت فنر را نمایش میدهد. این ثابت به صورت آزمایشگاهی برای فنرهای مختلف اندازهگیری میشود. همچنین x در رابطه بالا، میزان جابهجایی فنر از حالت تعادل را بیان میکند. در برخی کتب، حالت تعادل را «حالت خنثی» (Neutral Length) نیز مینامند. حالت تعادل، حالتی است که در آن، هیچ نیرویی باعث فشردگی یا کشیدگی فنر نمیشود. این نقطه را معمولا با x=0 و در مبدا مختصات نمایش میدهند.
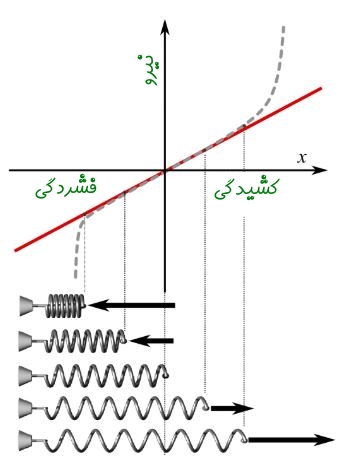
رابطه میان نیرو و تغییر طول فنر را میتوان با استفاده از شکل زیر نمایش داد. همانطور که مشاهده میشود، در محدوده معینی از کشیدگی یا فشردگی، رابطه میان نیرو و تغییر طول به صورت خطی است.
در ادامه، هدف ما به دست آوردن رابطهای برای کار انجام شده توسط فنر است. مفهوم بقای انرژی مکانیکی بیان میکند که کار انجام شده در یک سیستم جرم و فنر پایستار با مقدار انرژی ذخیره شده در این سیستم برابر است.
در این حالت، فرض کنید که x=0 و x=xf (مقداری مثبت)، به ترتیب مکان ابتدایی و انتهایی جعبهای را نشان میدهد که به قسمت آزاد فنر متصل است. توجه شود که سمت دیگر فنر به دیوار متصل شده است. مقدار کار انجام شده روی فنر در این حالت با استفاده از رابطه زیر به دست میآید.
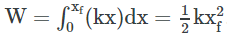
همانطور که میدانیم، رابطه کلی محاسبه کار به صورت ضرب داخلی دو بردار نیرو و جابهجایی به شکل زیر است.
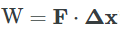
توجه شود که نیرویی که باعث کشیدگی فنر میشود با جابهجایی فنر همجهت است. بنابراین مقدار کار محاسبه شده در نهایت علامت مثبت دارد. این مورد در رابطه کار که به صورت انتگرالی محاسبه شد، نیز مشاهده میشود. نکته مهمی که در تمام مسائل باید به آن دقت کرد این است که علامت مثبت و منفی نیرو و کار کاملا به این نکته بستگی دارد که خواسته مسئله کار انجام شده توسط جسم یا کار انجام شده روی جسم است.
در ادامه، فرض کنید که فنر از موقعیت x=xf یکباره رها شود. در این شرایط، انرژی پتانسیل ذخیره شده در فنر، کم کم به انرژی جنبشی جعبه متصل به انتهای آزاد فنر، تبدیل میشود. در صورتی که از نیروهای اصطکاک صرف نظر شود، بقای انرژی مکانیکی بیان میکند که مجموع انرژی پتانسیل و جنبشی در تمام xها ثابت است.
در این حالت، جعبه متصل به فنر دائما بین نقطه x=-xf و x=xf نوسان میکند و تبدیل انرژی جنبشی به انرژی پتانسیل و برعکس به صورت پیوسته صورت میگیرد.
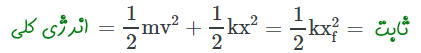
این رابطه بقای انرژی مکانیکی را نمایش میدهد. توجه شود که وقتی جعبه متصل به انتهای آزاد فنر، در نقطه x=xf قرار دارد، سرعت آن برابر با صفر است. نکته دیگر این است که وقتی جعبه متصل به فنر از نقطه x=0 عبور میکند، سرعت آن ماکزیمم است و با استفاده از رابطه زیر محاسبه میشود.
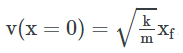
بنابراین مشاهده شد که انرژی کلی، شامل انرژی پتانسیل و جنبشی است و انرژی پتانسیل یک جسم را میتوان برابر با اختلاف انرژی آن جسم در یک موقعیت، نسبت به انرژی آن در مکان مرجع معرفی کرد.
همچنین مشاهده شد که به صورت کلی، انرژی پتانسیل، شامل انرژی پتانسیل کشسانی، گرانشی و الکتریکی است و کار ناشی از نیروی کشسانی را انرژی پتانسیل کشسانی مینامند و کار ناشی از نیروی گرانش، انرژی پتانسیل گرانشی نامیده میشود. همچنین کار ناشی از نیروی کولن را به عنوان انرژی پتانسیل الکتریکی معرفی میکنند.
این مطلب ابتدا به بررسی مفهوم انرژی پتانسیل و رابطه کلی آن پرداخته و سپس انواع انرژی پتانسیل و روابط حاکم بر آنها را مورد مطالعه قرار داده است.
در صورتی که به مباحث ارائه شده، علاقهمند هستید و قصد یادگیری در زمینههای مطرح شده در فیزیک پایه و مکانیک را دارید، آموزشهای زیر به شما پیشنهاد میشود:
- مجموعه آموزشهای فیزیک
- مجموعه آموزشهای دروس مهندسی مکانیک
- آموزش فیزیک پایه ۱
- آیرودینامیک (Aerodynamics) چیست؟ — از صفر تا صد
- نیروهای پایستار و ناپایستار — به زبان ساده
- مرکز جرم (Centre of Mass) — به زبان ساده
- مومنتوم خطی (Linear Momentum) در سیالات — از صفر تا صد
- قضیه کار و انرژی (Work-Energy Theorem) — آموزش سریع و ساده












سلام وقت بخیر
در رابطه با مبحث انرژی پتانسیل کشسانی فنر
میتونیم مقدار x رو اختلاف بین حالت تعادل فنر و مقدار فشردگی یا کشیدگی فنر در نظر گرفت؟
درود . تعریفی که واسه انرژی پتانسیل گرانش نوشتید اشتباه است . انرژی پتانسیل نتیجه کار نیروی گرانش است نه مقدار کاری که برای غلبه بر نیروی گرانشی انجام میدهیم. لطفا اصلاح کنید
سلام و روز شما به خیر؛
انرژی پتانسیل نتیجه کار نیروی گرانش نیست و همان طور که از روابط مشخص است علامت کار و نیروی پتانسیل خلاف یکدیگر است یعنی داریم W=−ΔU. در حقیقت با انجام کار در خلاف جهت نیروی گرانش این کار به صورت انرژی پتانسیل در جسم ذخیره میشود.
از اینکه با مجله فرادرس همراه هستید خرسندیم.