فرادرسمتغیر تصادفی و توزیع پارتو (Pareto Distribution) — مفاهیم و خصوصیات
همانطور که در دیگر نوشتارهای فرادرس با موضوع «تابع توزیع احتمال» خوانده‌اید، می‌دانید که توزیع‌های آماری به معرفی رفتار پدیده‌های تصادفی می‌پردازند. تا به حال با توزیع‌های مختلفی مانند توزیع نرمال یا گوسی (Normal)، دوجمله‌ای (Binomial)، گاما (Gamma)، توزیع کوشی (Cauchy) و چند توزیع دیگر آشنا شده‌اید. در این میان به بررسی «توزیع پارتو» (Pareto Distribution) می‌پردازیم که بسیاری از پدیده‌های طبیعی بخصوص متغیرهای درآمد و میزان جمعیت را مدل سازی می‌کند. توزیع پارتو دارای کاربردهای فراوانی در علوم اقتصادی و بیمه‌ای است و به همین علت دارای اهمیت زیادی است. اصل ۸۰-۲۰ یا قانون پارتو نیز برگرفته از این توزیع است. توزیع متغیر تصادفی پارتو دارای «چولگی» (Skewed) و «دم سنگین» (Heavy Tail) است. بنابراین در بیان بیشتر پدیده‌هایی که دارای توزیع نرمال نیستند، کاربرد خواهد داشت. در این نوشتار به معرفی متغیر تصادفی و توزیع پارتو پرداخته و در مورد خصوصیات هر یک بحث خواهیم کرد.
از آنجایی که در این مطلب از متغیر تصادفی و تابع احتمال صحبت به میان خواهد آمد بهتر است ابتدا مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کرده باشید. همچنین اگر قانون پارتو علاقمند هستید، خواندن مطلب قانون پارتو (Pareto Law) --- تعریف و کاربردهای آن نیز خالی از لطف نیست.
توزیع پارتو (Pareto Distribution)
متغیر تصادفی با توزیع پارتو یا «توزیع توانی» (Power Distribution) کاربردهای زیادی در علوم مختلف از جمله فیزیک، علوم طبیعی و امور مالی پیدا کرده‌اند. به همین علت توجه زیادی به این توزیع شده است تا بتوان به رفتار پدیده‌هایی که از این توزیع پیروی می‌کنند پی برد.
این توزیع به افتخار فعالیت‌های دانشمند و مهندس ایتالیایی «ویلفردو پارتو»، (Vilfredo Preto) توزیع پارتو نامیده شده است. این توزیع به علت هماهنگی با اصل ۸۰-۲۰ یا قانون پارتو شهرت یافته است.
تابع توزیع احتمال تجمعی (Cumulative Distribution Function)
اگر X یک متغیر تصادفی با توزیع پارتو (نوع یک) باشد، «تابع بقا» (Survival Function) برای آن با $$\overline{F}_X(x)$$ نشان داده شده و به صورت زیر نوشته می‌شود.
$$\large \overline{F}_X(x)=P(X>x)=\begin{cases}\big{(}\frac{x_m}{x}\big{)}^{\alpha} & x \geq x_m\\ 1 & x <x_m\end{cases}$$
در این حالت می‌نویسیم $$X\sim Pa(x_m,\alpha)$$ است و می‌خوانیم X دارای توزیع پارتو با پارامترهای $$x_m$$ و $$\alpha$$ است.
منظور از $$x_m$$ در اینجا حداقل مقدار ممکن برای X است که به «پارامتر مقیاس» (Scale Parameter) معروف است. همچنین $$\alpha$$ نیز «پارامتر شکل» (Shape Parameter) با مقدارهای مثبت است. از آنجایی که تابع بقا بیانگر احتمال مشاهده مقدار در دم‌ها است، برای معرفی توزیع پارتو از تابع بقا استفاده شده است. به این ترتیب مشخص است که با بزرگتر شدن مقدار $$\alpha$$ از ۱، این احتمال کاهش یافته و با نزدیک شدن $$\alpha$$ به صفر، مقدار احتمال مشاهده داده‌ای در دم‌های توزیع، افزایش می‌یابد.
نکته: اگر $$F_X(x)=P(X<x)$$ همان تابع توزیع تجمعی متغیر تصادفی X باشد، منظور از تابع بقا $$1-F_X(x)$$ است.
بنابراین برای این متغیر تصادفی تابع توزیع احتمال تجمعی به صورت زیر خواهد بود.
$$\large F_X(x)=1- \overline{F}_X(x)=1 -\big(\frac{x_m}{x}\big)^{\alpha} $$
با توجه به شکل تابع توزیع احتمال تجمعی، مشخص است که «تکیه‌گاه» (Support) برای متغیر تصادفی X به صورت $$S=[x_m,\infty)$$ است. پس این متغیر تصادفی از نوع پیوسته خواهد بود.
تابع احتمال متغیر تصادفی پارتو (Density Probability Function)
با توجه به رابطه‌ای که بین تابع توزیع احتمال تجمعی و تابع چگالی احتمال وجود دارد، به راحتی می‌توان تابع چگالی این متغیر تصادفی را به صورت زیر محاسبه کرد.
$$\large f_X(x)=-\frac{d\overline{F}_X(x)}{dx}=\frac{\alpha x_m^{\alpha}}{x^{\alpha+1}} $$
در تصویر زیر نمودار تابع احتمال برای این متغیر تصادفی برحسب مقدارهای مختلف پارامتر شکل و مقدار $$x_m=1$$ ترسیم شده است.
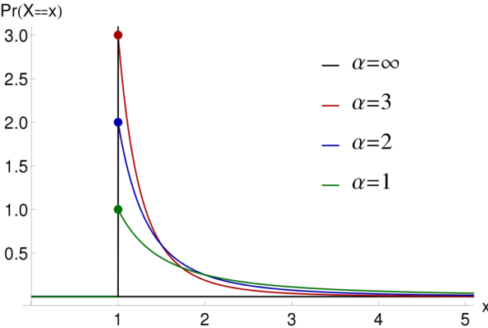
نکته: گاهی به پارامتر $$\alpha$$، شاخص دمی (Tail index) نیز می‌گویند زیرا بیانگر میزان احتمالی است که در دم‌ها ظاهر می‌شود. هر چه این شاخص بیشتر باشد احتمال مشاهده مقدار در دم‌های توزیع کمتر می‌شود. این خصوصیت در تصویر بالا به خوبی دیده می‌شود. خط قرمز رنگ برای مقدار $$\alpha=3$$ ترسیم شده است.به نظر می‌رسد که این نمودار نسبت به بقیه خطوط، شانس کمتری برای مشاهده نقاط دور افتاده خواهد داشت. در حالیکه خط سبز رنگ با $$\alpha=1$$ دارای نموداری است که انتهای آن از منحنی‌های دیگر بالاتر به نظر می‌رسد. پس شانس مشاهده مقدارهای بزرگ، بیشتر است. در این حالت می‌گویند توزیع «دم سنگین» است.
حال به شکل منحنی تابع توزیع احتمال تجمعی برای این متغیر تصادفی می‌پردازیم. به ازای مقدارهای مختلف $$\alpha$$ و باز هم با فرض $$x_m=1$$ نمودار تابع توزیع تجمعی احتمال متغیر تصادفی پارتو در تصویر زیر رسم شده است.
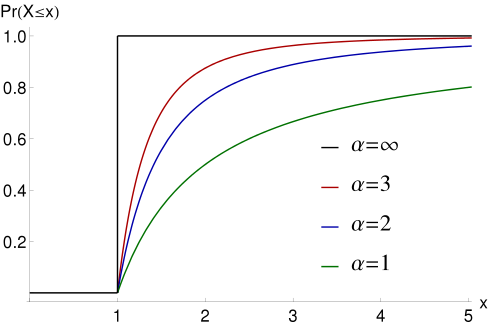
نکته: اگر مقدار پارامتر $$\alpha=1.16$$ باشد، می‌توان اصل پارتو را نتیجه گرفت. خوشبختانه بیشتر پدیده‌های طبیعی و فعالیت‌های انسانی از این توزیع با پارامتر شکل $$\alpha=1.16=\log_45$$ هستند.
امید ریاضی و واریانس برای متغیر تصادفی پارتو
با توجه به مفهوم امید ریاضی و واریانس متغیر تصادفی، برای توزیع پارتو، امید ریاضی و واریانس به صورت زیر قابل محاسبه است.
$$\large E(X) ={\begin{cases}\infty &{\text{for }}\alpha \leq 1\\{\dfrac {\alpha x_{\mathrm {m} }}{\alpha -1}}&{\text{for }}\alpha >1\end{cases}}$$
نکته: متغیر تصادفی پارتو، به ازاء پارامتر $$\alpha\leq 1$$ دارای امید ریاضی نیست. ولی برای $$\alpha>1$$ تابعی خطی از $$x_m$$ و تابعی نزولی از $$\alpha$$ است.
واریانس برای متغیر تصادفی پارتو نیز برطبق رابطه زیر بدست می‌آید.
$$\large Var(X) =\begin{cases}\infty &{\text{for }}\alpha \leq 2\\{\dfrac {x_{\mathrm {m} }^{2}\alpha }{(\alpha -1)^{2}(\alpha -2)}}&{\text{for }}\alpha >2\end{cases}$$
به این ترتیب مشخص است که به ازای $$\alpha\leq 2$$ متغیر تصادفی پارتو واریانس متناهی ندارد.
صورت‌های دیگر توزیع پارتو (Pareto Types I-IV)
براساس شکل‌های گوناگونی که برای تابع بقای متغیر تصادفی پارتو در نظر گرفته شده است، توزیع‌های مختلفی نیز ایجاد شده است. در این حالت پارامتر $$x_m$$ که پارامتر مقیاس نامیده می‌شد به $$\sigma$$ تغییر یافته است. جدول زیر به معرفی این توزیع‌ها اختصاص یافته.
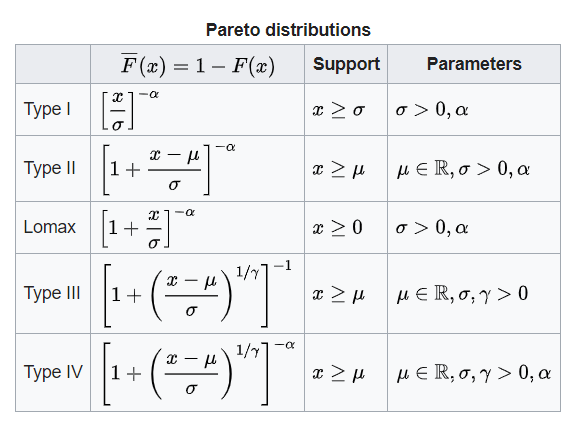
به این ترتیب $$\alpha$$ را «پارامتر دم» (Tail Index) و $$\mu$$ را نیز پارامتر مکان (Location) می‌نامند. همچنین $$\sigma$$ پارامتر مقیاس و $$\gamma$$ نیز «پارامتر نابرابری» (Inequality) در نظر گرفته شده است. اگر در توزیع پارتو از نوع II مقدار پارامتر مکان برابر با صفر باشد، توزیع حاصل را «توزیع لوماکس» (Lomax Distribution) می‌نامند.
نکته: به نظر می‌رسد که توزیع پارتو از نوع IV حالت کلی‌تری از توزیع‌های دیگر است. به این ترتیب رابطه زیر را بین این توزیع و بقیه انواع توزیع‌های پارتو می‌توان پیدا کرد. توزیع پارتو از نوع IV (نوع چهارم) را به صورت $$X\sim Pa_{_{IV}}(\mu,\sigma,\gamma,\alpha)$$ نشان می‌دهند.
$$\large P(IV)(\sigma, \sigma, 1, \alpha) = P(I)(\sigma, \alpha),\\ \large P(IV)(\mu ,\sigma ,1,\alpha )=P(II)(\mu ,\sigma ,\alpha ),\\ \large P(IV)(\mu ,\sigma ,\gamma ,1)=P(III)(\mu ,\sigma ,\gamma ).$$
در جدول زیر نیز امید ریاضی و گشتاورهای این گروه از توزیع‌های پارتو دیده می‌شوند. (در این حالت $$\mu=0$$ در نظر گرفته شده است.)
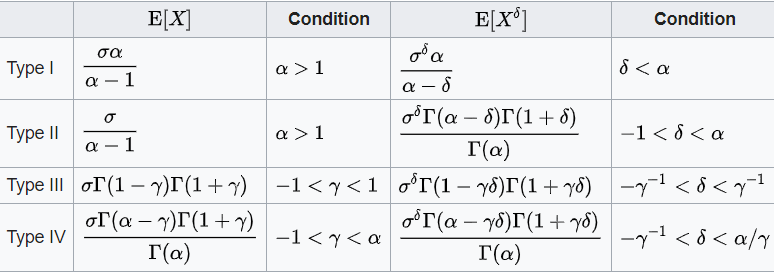
منظور از $$\Gamma(\alpha)$$، محاسبه تابع گاما در نقطه $$\alpha$$ است. برای آشنایی با این تابع به مطلب اصول شمارش و فاکتوریل — به زبان ساده مراجعه کنید.
کاربردهای توزیع پارتو
در فهرست زیر به معرفی پدیده‌های تصادفی می‌پردازیم که دارای توزیع پارتو هستند.
- اندازه شهرک‌ها و شهرها
- اندازه فایلهای منتقل شده روی خطوط اینترنت با پروتکل TCP/IP (تعداد فایلهای کوچک زیاد و تعداد فایلهای حجیم کم)
- نرخ خطای دستگاه‌های ذخیره سازی رایانه‌ها
- ارزش ذخایر نفتی در حوضچه‌های نفتی (حوضچه‌های غنی کم، در مقابل حوضچه‌های کم ارزش زیاد)
- ارزش بازگشت سرمایه استاندارد برای انواع سهام در بورس
- اندازه دانه‌های شن
- اندازه شهاب سنگ‌ها
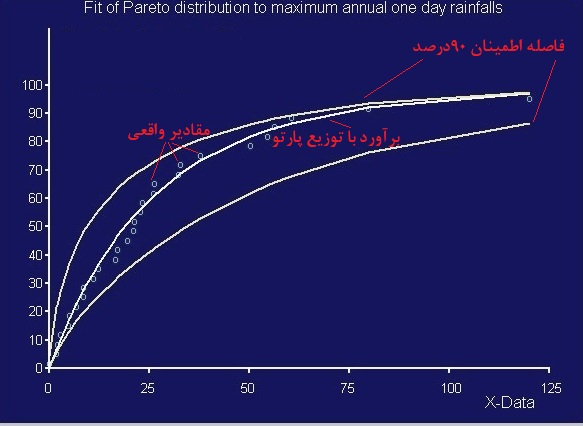
- حداکثر بارش در سال
نمودار زیر به بررسی نمودار توزیع فراوانی تجمعی حداکثر میزان بارش در سال پرداخته است. مشخص است که محور افقی میزان بارش و محور عمودی نیز فراوانی نسبی تجمعی برای این روز‌ها است. منحنی برازش شده و داده‌های واقعی در نمودار به همراه یک فاصله اطمینان ۹۰ درصد دیده می‌شود. این نمودار نشان می‌دهد که توزیع پارتو با توزیع واقعی داده‌ها مطابقت مناسبی دارد.
رابطه با قانون پارتو (Pareto's Rule)
قانون 20-80 یا اصل پارتو یکی از جالب‌ترین اصولی است که در مورد پدیده‌های طبیعی وجود دارد. به طور معمول گفته می‌شود که ۸۰٪ ثروت جهان در دست ۲۰٪ مردم است. در واقع این حقیقت برای پدیده‌های صحیح است که پارامتر توزیع پارتو ($$\alpha$$) برایشان برابر با تقریبا 1.161 باشد.
به این ترتیب براساس قواعد زیر می‌توان به اصل یا قانون 20-80 پی برد.
- درآمد افراد دارای توزیع پارتو با پارامتر $$\alpha>1$$ است.
- برای عدد $$p$$ که $$0\leq p \leq 0.5$$ باشد آنگاه $$100\times p$$ درصد از افراد دریافتی برابر با $$100\times (1-p)$$ درصد از مجموع درآمد‌ها را دارند.
- به همین ترتیب، برای مقدار حقیقی $$n>0$$، خواهیم داشت $$100\times p^n$$درصد از افراد درآمدی برابر با $$100 \times (1-p)^2$$ از درآمد کل را دارند.
این درصدها و قوانین فقط برای متغیر درآمد نخواهد بود بلکه برای هر متغیری تصادفی که دارای توزیع پارتو با پارامتر $$\alpha>1$$ باشد نیز صادق است.
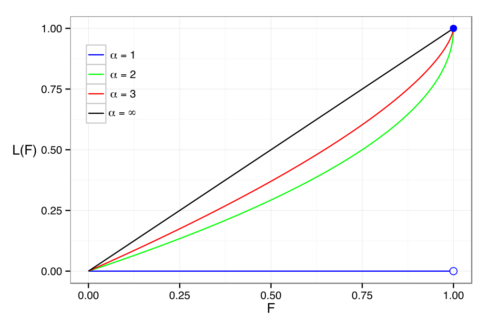
نمودار لورنز (Lorenz Curve)
در اقتصاد، منحنی لورنز یک روش برای نمایش توزیع درآمد یا ثروت است. این نمودار در سال 1905 توسط لورنز (Max O. Lorenz) اقتصاددان آمریکایی معرفی شد. این نمودار اغلب بوسیله رسم تابع احتمال تجمعی برحسب چگالی احتمال ایجاد می‌شود. محور افقی مقدار تابع احتمال تجمعی و محور عمودی نیز برحسب $$L(F)$$ نوشته می‌شود. این مقدار توسط رابطه زیر محاسبه می‌شود.
$$\large L(F)=\frac{\int_{x_\mathrm{m}}^{x(F)}xf(x)\,dx}{\int_{x_\mathrm{m}}^\infty xf(x)\,dx} =\frac{\int_0^F x(F')\,dF'}{\int_0^1 x(F')\,dF'}$$
در اینجا منظور از $$x(F)$$ چندک توزیع F در نقطه F است. برای توزیع پارتو این تابع به صورت زیر محاسبه می‌شود.
$$\large x(F)=\frac{x_\mathrm{m}}{(1-F)^{\frac{1}{\alpha}}}$$
به این ترتیب مقدار $$L(F)$$ محاسبه شده و نمودار ترسیم می‌گردد. شیوه محاسبه $$L(F)$$ در ادامه قابل مشاهده است.
$$\large L(F) = 1-(1-F)^{1-\frac{1}{\alpha}}$$
برای مثال توجه کنید که در گزارش بنیاد Oxfam-2016 بیان شده است که ۶۲ فرد ثروتمند به اندازه نصف مردم فقیر کل جهان ثروت دارند. بر این اساس می‌توان برآوردی برای پارامتر توزیع پارتو ($$\alpha$$) بدست آورد. فرض کنید $$\epsilon$$ برابر است با $$\tfrac{62}{(7\times 10^9)}$$. در نتیجه طبق رابطه $$L(F)$$ خواهیم داشت:
$$\large L(0.5)=1-L(1-\epsilon) = 1-0.5^{1-\tfrac{1}{\alpha}}= \epsilon^{1-\tfrac{1}{\alpha}}$$
در نتیجه مقدار $$\alpha=1.15$$ بدست خواهد آمد. پس ۹٪ ثروت جهان در اختیار این دو گروه است. ولی واقعیت این گونه است که 69٪ از بزرگسالان در جامعه فقیر جهان فقط ۳٪ از ثروت جهان را در اختیار دارند.
نکته: در اینجا $$\tfrac{62}{(7 \times 10^9)}$$ درصدی است که نسبت تعداد این ۶۲ نفر را به کل جمعیت جهان نشان می‌دهد. این مقدار همان مقدار $$p$$ در رابطه‌های بالا است.
اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
- آزمایش تصادفی، پیشامد و تابع احتمال
- مجموعه آموزش‌های SPSS
- آموزش آمار و احتمال مهندسی
- مجموعه آموزش‌های نرم‌افزارهای آماری
- جامعه آماری — انواع داده و مقیاس‌های آن‌ها
- تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
- فاصله اطمینان (Confidence Interval) — به زبان ساده
^^
با سلام و احترام. خواستم در مورد توزیع پارتو مطالب بیشتری بدانم.
سلام خواستم در مورد توزیع پارتو بدانم که نرخ شمستش افزایشی است یا کاهشی؟در مورد توزیع وایبول افزایشی است و در مورد توزیع نمایی کاهشی است حالا در مورد پارتو چگونه است؟