محاسبات توزیع نرمال در اکسل — از صفر تا صد

از آنجایی که متغیر تصادفی و توزیع نرمال و محاسبات مربوط به آن در بسیاری از علوم به کار گرفته می‌شود، لازم است که از نحوه بدست آوردن احتمال در این توزیع بیشتر مطلع باشیم. بنابراین در این نوشتار به بررسی چند مثال برای محاسبه توزیع نرمال می‌پردازیم.

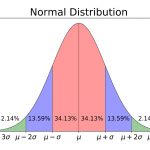
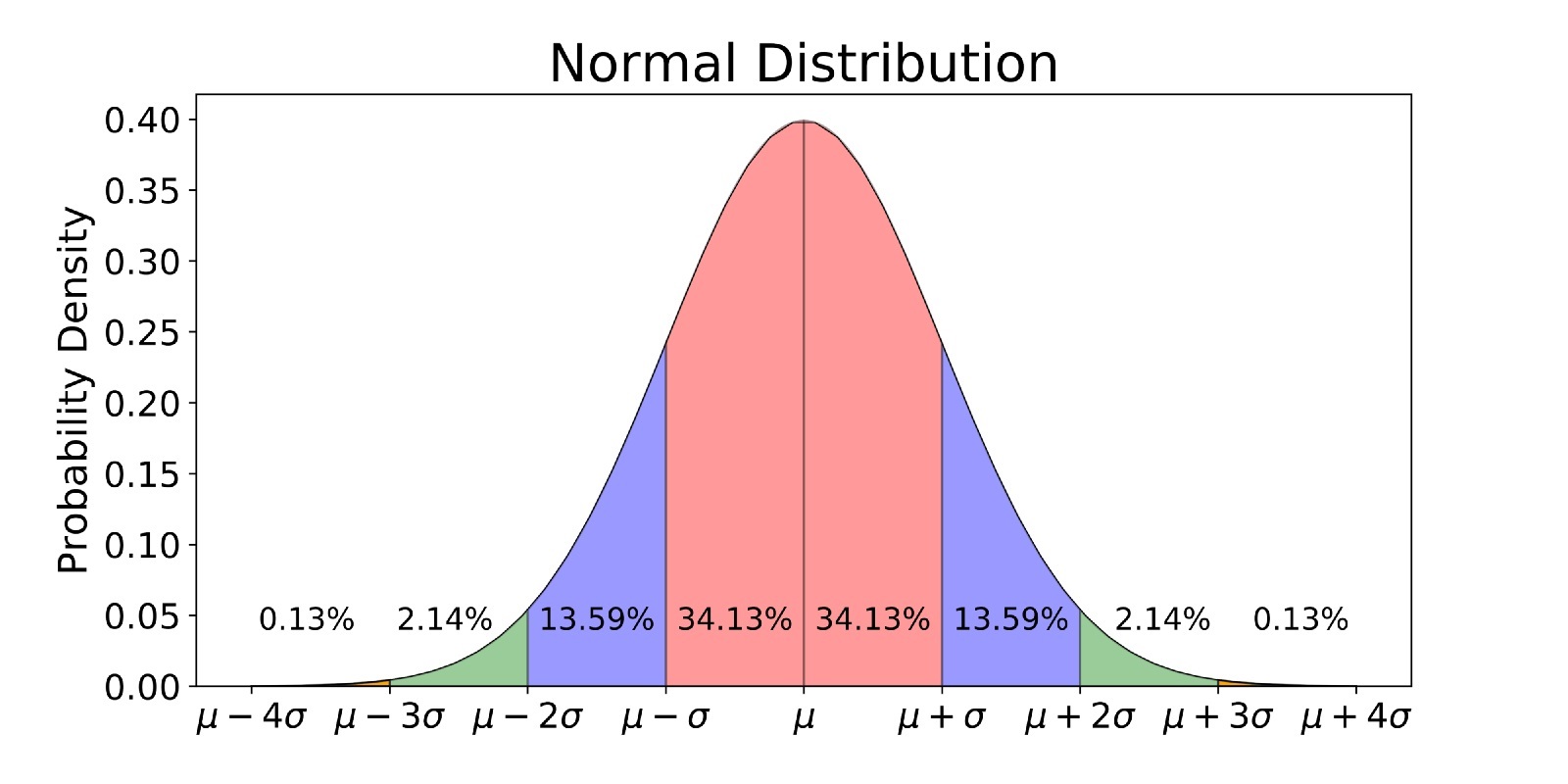
برای آشنایی بیشتر با متغیر تصادفی و توزیع نرمال بهتر است مطلب توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها را مطالعه کنید. البته در انتهای متن نیز برای محاسبه احتمالات متغیر تصادفی دو جمله‌ای از توزیع نرمال کمک خواهیم گرفت. بنابراین خواندن نوشتار متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده نیز خالی از لطف نیست.

توزیع نرمال و نرمال استاندارد

در دیگر نوشتارهای فرادرس با توزیع نرمال و نرمال استاندارد آشنا شده‌اید. اما در این قسمت سعی داریم به بررسی چند مثال و شیوه محاسبه احتمال و برخی خصوصیات این توزیع بپردازیم. اگر متغیر تصادفی $$X$$ دارای توزیع نرمال با میانگین $$\mu$$ و واریانس $$\sigma^2$$ باشد، می‌توانیم با یک تبدیل (که به تبدیل $$Z$$ یا Z-score معروف است) آن ر به توزیع نرمال استاندارد تبدیل کنیم که میانگین آن برابر با صفر و واریانس نیز برابر با ۱ است.

فیلم آموزش کاربرد اکسل Excel در مهندسی صنایع در فرادرس

کلیک کنید

به این ترتیب محاسبات برای پیدا کردن احتمال ساده‌تر خواهد شد.

$$\large Z=\dfrac{X-\mu}{\sigma}$$

رابطه ۱

براساس این تبدیل اگر $$X\sim N(\mu,\sigma^2)$$ باشد آنگاه $$Z\sim N(0,1)$$ است. به این ترتیب مشخص است که رابطه زیر نیز برقرار است.

$$\large X=\mu+Z\sigma$$

رابطه ۲

محاسبه احتمال بر اساس مقدار یا امتیاز استاندارد (Z-Score)

با توجه به مفهوم امتیاز استاندارد یا Z-Score به بررسی شیوه محاسبه احتمال براساس چند مثال خواهیم پرداخت. البته در ادامه نیز عکس این عمل را انجام می‌دهیم. به این معنی که براساس احتمال، نقطه‌ای را پیدا می‌کنیم که احتمال تا آن نقطه برابر با $$p$$ باشد. چنین نقطه‌ای را چندک $$p$$ام می‌گویند. برای پیدا کردن مقدار احتمال برای توزیع نرمال استاندارد معمولا از جدول‌های توزیع نرمال استاندارد استفاده می‌شود. شیوه به کارگیری این جدول‌ها در نوشتار توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها و جدول توزیع نرمال استاندارد – به زبان ساده آمده است. در ادامه با پرداختن به مثال‌هایی با توجه به این جدول‌ها و البته نرم‌افزار اکسل (MS Excel) بعضی از احتمالات را محاسبه خواهیم کرد.

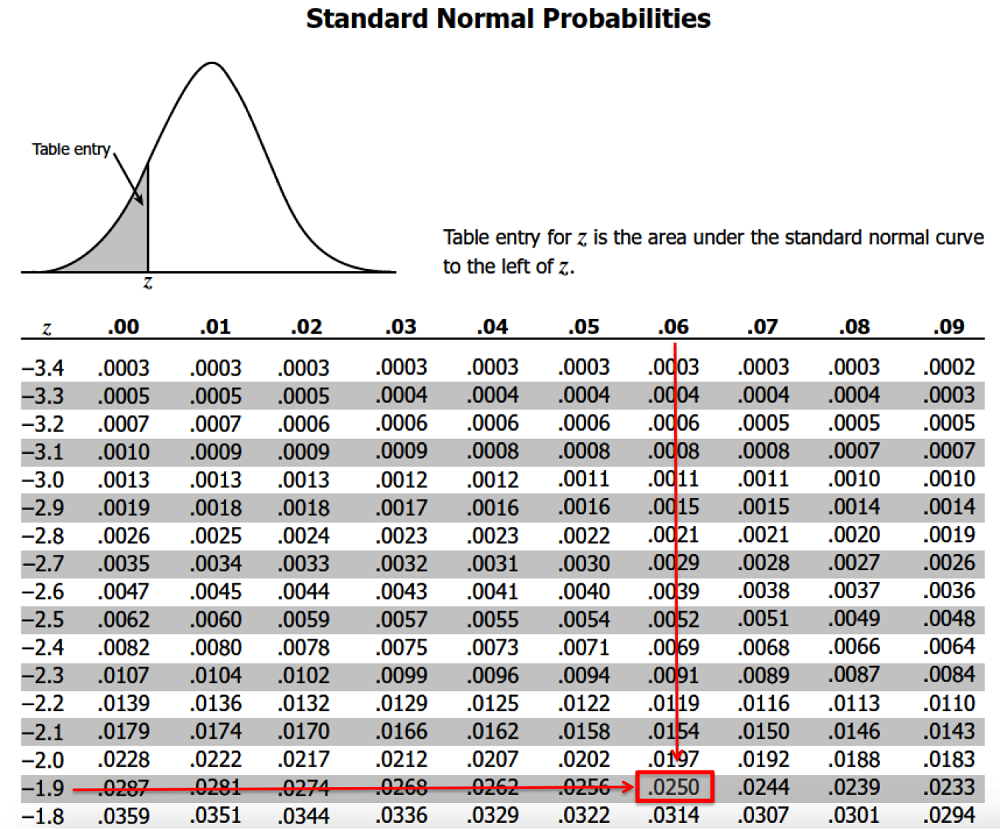
در تصویر زیر یک نمونه از جدول توزیع تجمعی احتمال نرمال را مشاهده می‌کنید. سطر اول و ستون اول از جدول برای تعیین مقدار $$z$$ به کار رفته و اعداد داخل جدول نشانگر احتمالات تا نقطه $$x$$ هستند.

مثال ۱‍

فرض کنید اندازه کفش مردان دارای توزیع نرمال با میانگین $$\mu=11$$ اینچ و انحراف استاندارد $$\sigma=1.5$$ اینچ باشد. احتمال اینکه فردی به فروشگاه مراجعه کند و کفش با اندازه بزرگتر از ۱۳ اینچ بخواهد چقدر است؟

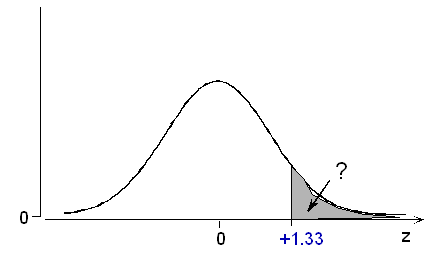
اگر $$X\sim N(11,1.5^2)$$ باشد، هدف محاسبه احتمال $$\large P(X>13)$$ است. مطابق با تصویر زیر به نظر می‌رسد که باید احتمال مربوط به ناحیه بالای ۱۳ اینچ در نمودار چگالی احتمال محاسبه شود. می‌دانیم که این احتمال برابر با سطح زیر منحنی (مساحت ناحیه خاکستری رنگ) در نمودار است.

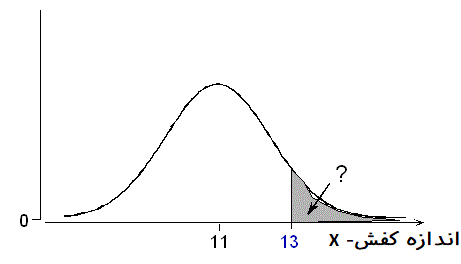
ولی بدست آوردن این احتمال و مساحت ناحیه خاکستری رنگ، از طریق انتگرال‌گیری مشکل است زیرا انتگرال تابع چگالی توزیع نرمال با روش‌های تحلیلی به سادگی بدست نمی‌آید. بنابراین باید به روش‌های تقریبی و عددی متکی باشیم. محاسبات مربوط به این احتمالات توسط روش‌های عددی در جدول‌های توزیع نرمال استاندارد منتشر شده است. از آنجایی که به جدول احتمال برای توزیع نرمال استاندارد دسترسی داریم، با استفاده از Z-Score که در رابطه ۱ معرفی شد، محاسبات را پی می‌گیریم.

$$\large z=\dfrac{x-\mu}{\sigma}=\dfrac{13-11}{1.5}=+1.33$$

بنابراین محاسبه احتمال به صورت زیر ساده می‌شود

$$P(X>13)=P(Z>+1.33)$$

با مراجعه به جدول یا برنامه‌های محاسباتی مانند اکسل مقدار این احتمال را به راحتی می‌توان بدست آورد.

$$\large P(Z>+1.33)=P(Z<-1.33)=0.0918$$

برای پیدا کردن این احتمال در مثال مورد نظر، به کمک اکسل کافی است از تابعی norm.dist به صورت زیر استفاده کنیم.

1=NORM.DIST(-1.33,0,1,TRUE)

به این ترتیب به نظر می‌رسد ۹٪ افراد مراجعه کننده به فروشگاه، خواهان کفش‌های با اندازه‌ بزرگتر از ۱۳ اینچ هستند.

نکته: از آنجایی که توزیع نرمال دارای خاصیت تقارن است می‌توان احتمال پیشامد $$X>x$$ را با احتمال پیشامد $$X<-x$$ یکسان در نظر گرفت.

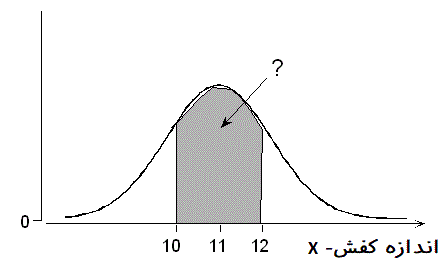
حال به بررسی احتمال این می‌پردازیم که فرد مراجعه کننده احتیاج به کفشی در حدود ۱۰ تا ۱۲ اینچ داشته باشد. باز هم محاسبه احتمال به صورت زیر خواهد بود.

$$\large P(10 \leq X \leq 12)$$

این احتمال مطابق با سطح ناحیه زیر منحنی تابع چگالی بین دو نقطه ۱۰ و ۱۲ است. محاسبه انتگرال برای چگالی نرمال در این قسمت نیز بسیار پیچیده و سخت است.

راه حل، استاندارد کردن متغیر تصادفی نرمال است. به این ترتیب محاسبات به صورت زیر انجام خواهد شد.

$$\large P(10\leq X \leq 12)=P(\dfrac{10-11}{1.5}\leq Z \leq \dfrac{12-11}{1.5})=P(-0.67 \leq Z \leq 0.67)$$

مطابق با نحوه محاسبه احتمال براساس تابع توزیع، نحوه پیدا کردن احتمال برای این پیشامد مطابق با رابطه‌هایی است که در ادامه قابل مشاهده است.

$$\large P(-0.67 \leq Z \leq 0.67) =P(Z\leq 0.67)-P(Z\leq -0.67)= 0.7486-0.2514=0.4972$$

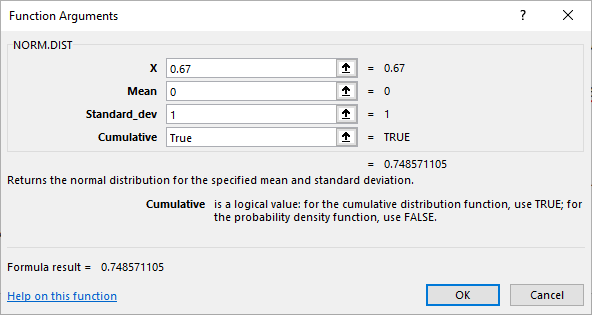
به این ترتیب مشخص می‌شود که حدود ۵۰٪ افراد احتیاج به کفشی در بازه ۱۰ تا ۱۲ اینچ دارند. البته باز هم با استفاده اکسل و تابع norm.dist مطابق با فرمول زیر، می‌توان به همین جواب رسید.

1=NORM.DIST(0.67,0,1,TRUE)-NORM.DIST(-0.67,0,1,TRUE)

نکته: در تابع norm.dist چهار پارامتر وجود دارد. پارامتر اول ($$X$$) مقداری است که احتمال تا آن نقطه باید محاسبه شود. پارامتر دوم (Mean) و سوم (Standard_dev) میانگین و انحراف استاندارد توزیع نرمال مورد نظر است. پارامتر چهارم (Cumulative) که مقداری منطقی است بیان می‌کند که آیا باید مقدار توزیع تجمعی برای توزیع نرمال محاسبه شود یا تابع چگالی احتمال. با انتخاب گزینه True برای این پارامتر، تابع احتمال تجمعی محاسبه خواهد شد.

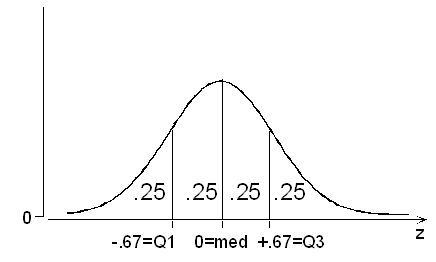
از این رابطه و نتیجه حاصل شده، متوجه می‌شویم که احتمال 0.7486 نشان می‌دهد، حدود ۷۵٪ افراد دارای اندازه پای کوچکتر از ۱۲ اینچ هستند. همچنین احتمال 0.2514 نیز بیانگر آن است که حدود یک چهارم افراد اندازه پایی کوچکتر از ۱۰ اینچ دارند. این واقعیت را می‌توان به این صورت نیز بیان کرد که ۲۵٪ مقدارهای توزیع نرمال استاندارد کمتر از 0.67- هستند. همچنین حدود 75٪ از داده‌های توزیع نرمال استاندارد در ناحیه کمتر از 0.67+ قرار دارند. به این ترتیب مشخص است که 0.67- چارک اول و 0.67 نیز چارک سوم توزیع اندازه کفش‌های استاندارد شده است. از طرفی چون میانگین و میانه (چارک دوم) در توزیع نرمال یکسان هستند، می‌توان چارک دوم یا میانه را هم صفر (میانگین توزیع نرمال استاندارد) در نظر گرفت.

نکته: در این مثال کران بالا و پایین برای محاسبه احتمال قرینه یکدیگر شدند. این امر به آن علت است که فاصله مقدارهای اصلی یعنی ۱۰ و ۱۲ از میانگین توزیع نرمال (۱۱ اینچ) یکسان بود در نتیجه فاصله‌ها نیز قرینه شدند. این اتفاق همیشگی نیست و در بسیاری از موارد ممکن است که اعداد حاصل قرینه یکدیگر نباشند.

مثال ۲

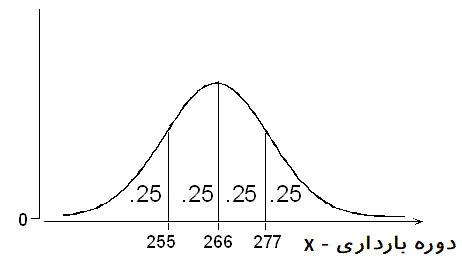
طول دوره بارداری (برحسب روز) در بین انسان‌ها یکسان نیست و بطور تصادفی تغییر می‌کند. فرض کنید این زمان از توزیع نرمال با میانگین ۲۶۶ و انحراف استاندارد 16 روز پیروی کند مطابق با آنچه در مثال قبل دیدیم می‌خواهیم چارک اول، دوم (میانه) و چارک سوم را براساس نمره استاندارد (Z-Score) با توجه به رابطه ۲ محاسبه کنیم.

قبلا دیدیم که برای توزیع نرمال استاندارد، چارک اول برابر است با 0.67- بنابراین برای طول دوره بارداری ($$X$$) که دارای توزیع $$X\sim N(266,16^2)$$ است، رابطه زیر به منظور محاسبه چارک‌ها، به کار خواهد آمد. اگر $$Q1$$ چارک اول و $$Q2$$ و $$Q3$$ به ترتیب چارک دوم (میانه) و چارک سوم باشند، خواهیم داشت:

$$\large Q1=266-0.67(16)=255$$

همین محاسبات را برای بدست آوردن میانه (چارک دوم) و چارک سوم نیز به کار می‌بریم.

$$\large Q2=median=mean=266-0\times(16)=266$$

$$\large Q3=266+0.67(16)=277$$

به این ترتیب مشخص است که احتمال آنکه طول دوره بارداری کمتر از 255 روز باشد، تقریبا ۲۵٪ است یا به بیان دیگر، ۲۵٪ افراد دوره بارداری کمتر از ۲۵۵ روز دارند. همچنین احتمال اینکه این دوره کمتر از ۲۷۷ روز باشد حدود ۷۵٪ خواهد بود و به طور متوسط این دوره ۲۶۶ روز در نظر گرفته می‌شود. به این ترتیب متوجه می‌شویم که ۲۵٪ افراد دوره بارداری بیش از ۲۷۷ روز داشته ولی متوسط دوره بارداری ۲۶۶ روز است.

اگر بخواهیم احتمال پیشامد اینکه فردی دوره بارداری کمتر از ۲۴۶ روز داشته باشد را محاسبه کنیم به روش زیر عمل می‌کنیم.

$$\large P(X\leq 246)=P(\dfrac{X-\mu}{\sigma}\leq \dfrac{246-266}{16})=P(Z\leq -1.25)=0.1056$$

این احتمال نشان می‌دهد که فقط ۱۰٪ افراد دچار زایمان زودرس می‌شوند. بر همین اساس نیز احتمال آنکه دوره بارداری بیش از 240 روز باشد به شکل زیر بدست می‌آید.

$$\large P(X\geq 240)=P(\dfrac{X-\mu}{\sigma} \geq \dfrac{240-266}{16})=P(Z\geq -1.63)=P(Z\leq +1.63)=0.9484$$

این امر نشان می‌دهد که احتمال اینکه دوره بارداری بیش از ۲۴۰ روز باشد بسیار محتمل است. به نظر شما احتمال اینکه این دوره بیش از ۵۰۰ روز باشد چقدر است؟ مقدار ۵۰۰ نسبت به میانگین دوره (۲۶۶ روز) بسیار دور است. اگر ملاک دوری یا نزدیکی را انحراف معیار قرار دهیم به نظر می‌رسد که مقدار ۵۰۰، بیش از ۱۴ برابر انحراف معیار از میانگین دور است.

$$\large \dfrac{500-266}{16}=14.625$$

در نتیجه باید مقدار احتمال برای این پیشامد، بسیار کوچک باشد. براساس فرمولی که در اکسل خواهیم نوشت این احتمال را محاسبه می‌کنیم.

$$\large P(X>500)=1-P(X<500)=1-1=0$$

1=1-NORM.DIST(500,266,16,TRUE)

به نظر می‌رسد که این پیشامد تقریبا غیرممکن است زیرا احتمال آن برابر با صفر است.

نکته: در این فرمول اکسلی، بدون استاندارد کردن متغیر تصادفی، محاسبه احتمال را انجام داده‌ایم. برای انجام این کار کافی است میانگین و انحراف معیار توزیع مورد نظر را برای تابع norm.dist مشخص کنید.

پزشک برای تعیین پایان وقت بارداری و زایمان می‌خواهد یک محدوده زمانی در نظر بگیرید. او معتقد است که احتمال اینکه  زایمان فردی در بازه ۲۳۵ تا ۲۹۵ روز صورت بگیرد، بیش از ۹۰٪ است. آیا شما با توجه به اطلاعاتی که در مورد توزیع تصادفی دوره بارداری دارید، نظرش را تایید می‌کنید؟

برای سنجش صحت نظریه پزشک از احتمالات توزیع نرمال روابط زیر به کمک ما می‌آیند.

$$\large P(235\leq X\leq 295)=P(-1.94\leq Z \leq +1.81)=P(Z\leq 1.81)-P(Z\leq -1.94)=\\ \large 0.9649-0.0262=0.9387$$

به نظر می‌رسد که گفته پزشک برمبنای آمار و احتمال صورت گرفته است و باید به آن اطمینان داشت.

محاسبه چندک‌های توزیع نرمال (مقدار Z-Score)

همانطور که قبلا توضیح داده شد، «چندک‌ها» (Quantiles)، مقدارهایی از تکیه‌گاه متغیر تصادفی هستند که میزان احتمال تا آن نقطه برابر با $$p$$ است. در توزیع احتمالاتی، برای محاسبه این نقطه‌ها باید از «جدول توزیع‌ احتمال تجمعی» (Cumulative Probability Table) استفاده کرد. در ادامه به بررسی مثال‌هایی در این زمینه برای توزیع نرمال، خواهیم پرداخت.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

مثال 3

باز هم به مثال اندازه کفش برمی‌گردیم. با توجه به اطلاعات قبلی می‌دانیم که توزیع احتمالی برای اندازه کفش افراد از توزیع نرمال با میانگین ۱11 و انحراف استاندارد (انحراف معیار) ۱.۵ اینچ پیروی می‌کند. اگر بدانیم 4٪ خریداران کودک هستند، اندازه کفشی که باید برای این گروه سفارش دهیم حداکثر چقدر است؟

اگر $$X$$ را متغیر تصادفی برای اندازه کفش در نظر بگیریم می‌دانیم که توزیع آماری و احتمالی آن به صورت $$X\sim N(11,1.5)$$ است. مطابق پرسش مربوطه به دنبال نقطه‌ای از این توزیع هستیم که احتمال تا آن نقطه برابر با 0.04 باشد.

$$\large P(X\leq x)=0.04\rightarrow P(\dfrac{X-\mu}{\sigma}\leq \dfrac{x-11}{1.5})=P(Z\leq z)=0.04$$

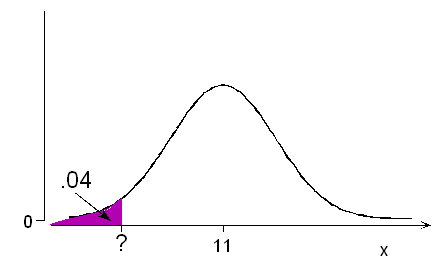
مطابق با جدول‌های توزیع احتمال تجمعی نرمال می‌توان به عدد 0.0401 رسید که مربوط به نقطه $$z=-1.75$$ است. به عبارت دیگر احتمال آن که مقدار متغیر تصادفی $$Z$$ کمتر از $$-1.75$$ باشد برابر با 0.0401 است.

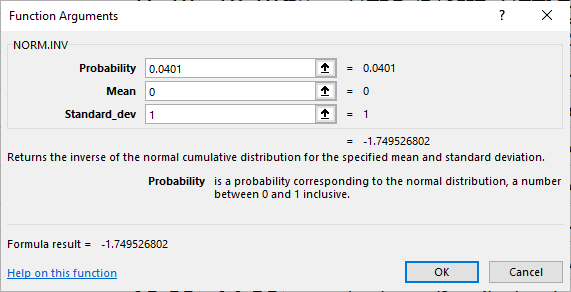
البته برای محاسبه این مقدار از توابع آماری اکسل نیز می‌توان استفاده کرد. کافی است از تابع norm.inv یا norm.s.inv استفاده کنید. در اولی باید میانگین و انحراف استاندارد توزیع نرمال را مشخص کنید ولی در دومی (norm.s.inv) فقط کافی است مقدار احتمال مشخص شود زیرا براساس توزیع نرمال استاندارد با میانگین صفر و واریانس ۱ محاسبات را انجام می‌دهد.

1=NORM.INV(0.0401,0,1)
2
3=NORM.S.INV(0.0401)

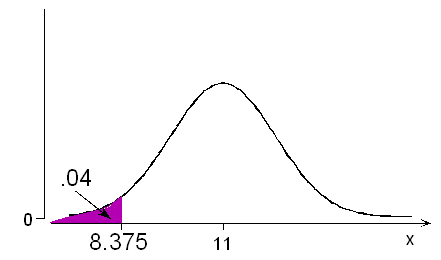
پاسخ برای هر دو فرمول به صورت $$-1.749526802$$ خواهد بود. حال این مقدار را که براساس توزیع نرمال استاندارد است، تبدیل به توزیع نرمال با میانگین ۱۱ و انحراف استاندارد 1.5 اینچ می‌کنیم. کافی است از رابطه ۲ کمک بگیریم.

$$\large X= \mu+zscore\times \sigma=11-1.75(1.5)=8.375$$

بنابراین باید ۴٪ کفش‌های سفارشی از 8.5 اینچ کوچکتر باشند.

نکته: تابع norm.inv معکوس تابع احتمال متغیر تصادفی نرمال است و برای محاسبه صدک‌های توزیع نرمال به کار می‌رود. این تابع دارای سه پارامتر است. پارامتر اول (Probability) درصد مربوط به صدک را مشخص می‌کند. به کمک پارامتر‌های دوم (Mean) و سوم (Standard_dev)، میانگین و انحراف استاندارد توزیع نرمال قابل تعیین است. تابع norm.s.inv نیز مشابه این تابع است با این تفاوت که صدک‌ها را برای توزیع نرمال استاندارد محاسبه می‌کند و از آنجایی که در این توزیع میانگین برابر با صفر و انحراف معیار نیز مقدار ۱ است، احتیاجی به تعیین میانگین و انحراف استاندارد توزیع نیست.

به عنوان سوال دوم، اگر بدانیم 10٪ بزرگسالان، بزرگ-پا هستند، حداقل اندازه کفش مناسب برای آن‌ها چه اندازه‌ای است؟

مشخص است که در اینجا به دنبال نقطه‌ای هستیم که احتمال از آن نقطه به بعد برابر با 0.01 باشد. از آنجایی که جدول‌های توزیع احتمال تجمعی نرمال استاندارد، به شکلی تدوین شده‌اند که احتمال تجمعی را برای $$Z\leq z$$ محاسبه می‌کنند، نمی‌توان به سادگی از آن‌ها برای پاسخ به این سوال استفاده کرد. به این ترتیب به نظر می‌رسد که باید با روش دیگری نقطه چندک مربوط به این سوال را جستجو کرد.

با توجه به تقارن توزیع نرمال از دو روش که در ادامه مورد بررسی قرار می‌گیرد، برای پاسخ به این پرسش استفاده خواهیم کرد.

روش اول:

با توجه به جدول توزیع نرمال استاندارد نقطه‌ای که احتمال تا آن نقطه برابر با 10٪ است (صدک ۱۰ام) برابر است با $$-1.28$$ براساس تقارن، 10٪ نقطه‌ها نیز بیشتر از $$1.28$$ هستند. بنابراین مطابق با رابطه ۲ خواهیم داشت:

$$\large X=\mu+Z\times \sigma=11+1.28\times 1.5=12.92$$

به این ترتیب به نظر می‌رسد که ۱۰٪ مشتریان، احتیاج به کفشی بزرگتر از 13 اینچ دارند.

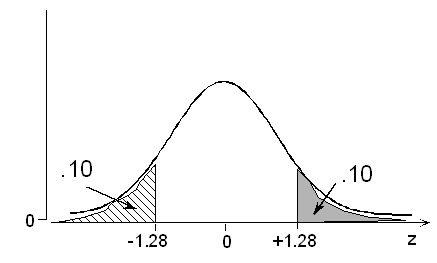
روش دوم:

همانطور که مشخص است به دنبال نقطه‌ یا اندازه کفشی هستیم که ۱۰٪ مشتریان به دنبال اندازه کفشی بزرگتر از آن هستند. می‌توان این نقطه را مشابه نقطه‌ای در نظر گرفت که ۹۰٪ مشتریان به دنبال کفشی کوچکتر از آن هستند. بنابراین باید مطابق با رابطه زیر عمل کنیم.

$$\large P(X>x)=0.1 \rightarrow 1-P(X>x)=P(X\leq x)=1-0.1=0.9$$

حال بدون در نظر گرفتن تقارن نیز می‌توان به جواب رسید. مطابق با جدول توزیع نرمال استاندارد این نقطه برابر است با 1.28+ بنابراین براساس رابطه ۲ خواهیم داشت.

$$\large X=\mu+Z\times \sigma+=11+1.28\times 1.5=12.92$$

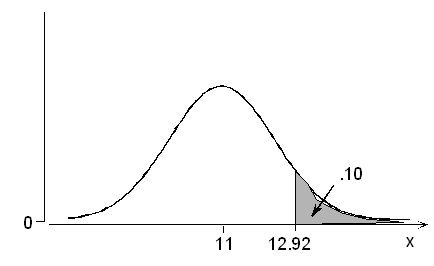
نکته: در این روش به جای محاسبه احتمال برای پیشامد $$X>x$$ از پیشامد متمم آن $$X$$ استفاده کردیم.

مثال ۴

یک رستوران معتقد است که میزان هزینه‌ای که مشتریان برای صرف غذا می‌پردازند دارای توزیع نرمال با میانگین ۳۵ و انحراف استاندارد ۵ دلار است. به نظر شما اکثر مشتریان (مثلا ۹۷٪) تمایل به خرید غذا با حداکثر چه قیمتی دارند؟

به نظر می‌رسد که باید صدک ۹۷ توزیع نرمال را محاسبه کنیم. این محاسبه به صورت زیر نوشته شده است.

$$\large  P(X\leq x)=0.97 \rightarrow P(z \leq \dfrac{x-35}{5})=P(Z\leq z)=0.97$$

به این ترتیب با استفاده از جدول توزیع نرمال استاندارد، مقدار این این نقطه $$1.88$$ است. البته براساس تابع  norm.sinv در اکسل نیز می‌توان این محاسبه را انجام داد و صدک ۹۷ توزیع نرمال استاندارد را بدست آورد.

1=NORM.S.INV(0.97)

حال براساس رابطه ۲، صدک ۹۷ام برای توزیع نرمال استاندارد را به صدک ۹۷ام از توزیع نرمال با میانگین ۳۵ و انحراف استاندارد ۵ تبدیل می‌کنیم.

$$\large 35+1.88 \times 5 = 44.44$$

البته این مقدار را براساس تابع norm.inv اکسل نیز می‌توان به دست آورد. کافی است که علاوه بر درصد مربوط به صدک، میانگین و انحراف استاندارد توزیع مورد نظر را نیز مشخص کنیم. به این صورت پارامترهای این تابع به ترتیب برابر با 0.97، 35 و 5 خواهند بود. نتیجه محاسبه این تابع برابر با 44.40 است که تقریبا با مقدار محاسبه شده طبق رابطه ۲ یکسان به نظر می‌رسد. پس مشخص است که اکثر افراد تمایل دارند که هزینه تهیه غذا برایشان حدود ۴۴.۵ دلار باشد.

1=NORM.INV(0.97,35,5)

تقریب توزیع نرمال برای احتمال توزیع دو جمله‌ای

محاسبه احتمال برای توزیع دوجمله‌ای برای مقدارهای بزرگ $$n$$ مشکل است. با توجه قضیه حد مرکزی (Central Limit Theorem) می‌توان احتمالات مربوط به توزیع دوجمله‌ای را با توزیع نرمال تقریب زد. به یک مثال در این زمینه توجه کنید.

فیلم آموزش توزیع نرمال در آمار و کاربرد آن در علوم انسانی (رایگان) در فرادرس

کلیک کنید

مثال 5

فرض کنید متغیر تصادفی $$X$$ دارای توزیع دوجمله‌ای با پارامترهای $$n=20$$ و $$p=0.5$$ است. می‌دانیم که میانگین و واریانس این توزیع به ترتیب برابر با 10 و 5 هستند. در تصویر زیر نمودار مربوط به تابع احتمال توزیع دوجمله‌ای مورد نظر به همراه تابع چگالی توزیع نرمال با میانگین ۱۰ و واریانس ۵ ترسیم و مقایسه شده‌اند.

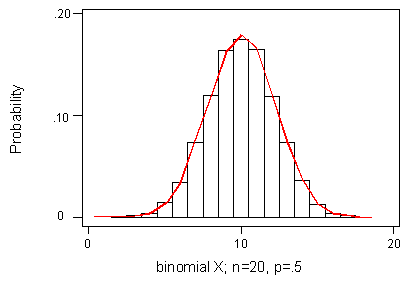
به نظر می‌رسد که این دو توزیع در این حالت مطابقت خوبی یا یکدیگر دارند. بنابراین برای محاسبه احتمال توزیع دوجمله‌ای که احتیاج به محاسبات زیاد (مثلا محاسبه $$20!$$ یا ۲۰ فاکتوریل) دارد، بهتر است از توزیع و جدول‌های توزیع نرمال استاندارد استفاده کنیم. در تصویر زیر یک نمونه از محاسبه احتمال برای توزیع دوجمله‌ای و تقریب آن توسط توزیع نرمال استاندارد دیده می‌شود.

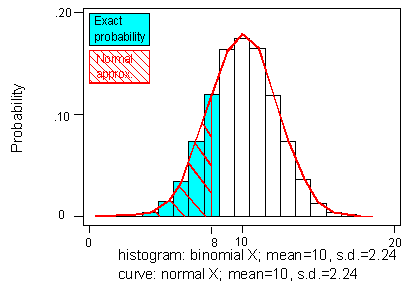
ناحیه آبی رنگ در این نمودار برای محاسبه احتمال $$P(X\leq 8)$$ طبق توزیع دوجمله‌ای، استفاده شده است.

$$\large P(X\leq 8)= 0.2517$$

با توجه به تقریب نرمال می‌توان گفت که توزیع تقریبی متغیر تصادفی $$X$$ به صورت $$X\sim N(10,5)$$‌ است.

$$\large \mu = np = 20 \times 0.5 =10, \;\; \sigma^2= np(1-p)=10\times 0.5 \times 0.5 = 5$$

بنابراین مطابق با توزیع نرمال رابطه زیر برقرار است.

$$\large P(X\leq 8) = P(\dfrac{8-10}{\sqrt{5}}\leq \dfrac{8-10}{2.24})=P(Z\leq -0.8944)=0.18555$$

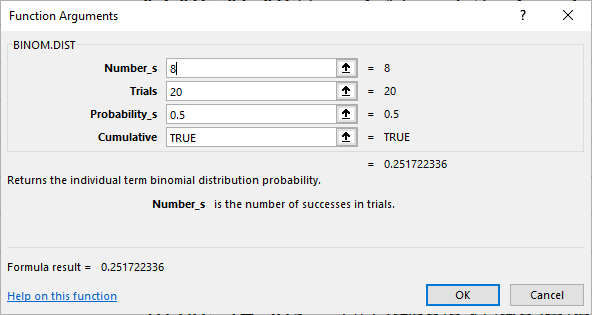
همانطور که مشخص است فاصله بین مقدار واقعی ($$0.2517$$) و مقدار تقریبی توسط توزیع نرمال ($$0.1855$$) برای احتمال فوق کم بوده و خطا حدود 7٪ است. البته با افزایش مقدار $$n$$ در توزیع دوجمله‌ای این تقریب بهتر و بهتر خواهد شد. برای انجام این محاسبات از توابع و فرمول‌های زیر در اکسل استفاده کرده‌ایم. تابع binom.dist برای محاسبه احتمال در توزیع دوجمله‌ای و تابع norm.dist نیز برای توزیع نرمال به کار گرفته می‌شود.

نکته: تابع binom.dist دارای چهار پارامتر است. پارامتر اول (Number_s) مقداری است که باید احتمال تا آن نقطه محاسبه شود. در حقیقت Number_s‌ همان تعداد موفقیت‌ها در آزمایش دوجمله‌ای است. پارامتر دوم (Trials) تعداد آزمایش‌ها در توزیع دوجمله‌ای را نشان می‌دهد. همچنین پارامتر سوم (Probability_s) نیز احتمال موفقیت در هر بار از آزمایش برنولی را مشخص می‌کند. در انتها پارامتر چهارم (Cumulative) نیز به کاربر اجازه می‌دهد یکی از دوحالت شیوه محاسبه توزیع تجمعی (TRUE) یا مقدار احتمال در یک نقطه (FALSE) از توزیع دوجمله‌ای را انتخاب کند.

1=BINOM.DIST(8,20,0.5,TRUE)
2
3=NORM.DIST(8,10,SQRT(5),TRUE)

نکته: برای آنکه بتوان به تقریبی مناسب برای توزیع دوجمله‌ای رسید باید شرایط زیر وجود داشته باشد.

$$\large E(X)=np \geq 10,\;\;\;\; Var(X)=np(1-p) \geq 10$$

به منظور بهبود تقریب توزیع نرمال از روشی دیگری که به نام «تصحیح پیوستگی» (Continuity Correction) معروف است، می‌توان استفاده کرد. از آنجایی که توزیع دوجمله‌ای گسسته بوده ولی توزیع نرمال از نوع پیوسته است، باید دقت اندازه‌گیری را نیز لحاظ کرد به این ترتیب اگر می‌خواهیم مقدار احتمال را در توزیع دوجمله‌ای تا نقطه ۸ محاسبه کنیم بهتر است هنگام استفاده از تقریب نرمال، احتمال را برای توزیع نرمال تا نقطه 8.5 بدست آوریم.

مطابق با این روش مقدار تقریبی احتمال دوجمله‌ای توسط توزیع نرمال بسیار دقیق‌تر خواهد شد. با توجه به مثال قبل محاسبه احتمال با این روش برابر است با $$0.2512$$ که به مقدار واقعی بسیار نزدیک‌تر است.

1=NORM.DIST(8.5,10,SQRT(5),TRUE)

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
• آزمون فرض میانگین جامعه در آمار — به زبان ساده

^^