دسته‌ بند بیز ساده (Naive Bayes Classifiers) – مفاهیم اولیه و کاربردها

در حوزه «یادگیری ماشین» (Machine Learning)، تکنیک و روش «دسته‌ بند بیز ساده» (Naive Bayes Classifiers) با بکارگیری قضیه بیز و فرض استقلال بین متغیرها، به عنوان عضوی از خانواده «دسته‌بندهای برمبنای احتمال» (Probabilistic Classifiers) قرار می‌گیرد. در سال‌های ۱۹۶۰ تحقیق و بررسی‌های زیادی پیرامون بیز ساده بخصوص در زمینه «بازیابی متن» (Text Retrieval) صورت گرفت و حتی امروز هم به عنوان ابزاری برای «دسته‌بندی متن» (Text Categorization) برای حل مسائلی مانند تشخیص «هرزنامه‌ها» (Spam Mails) به کار می‌رود. معمولا این کار به کمک برآورد تابع احتمال و از طریق فراوانی یا فراوانی نسبی کلمات در اسناد متنی صورت می‌گیرد.

به این ترتیب به کمک حداکثرسازی تابع درستنمایی (Likelihood maximization)، برآورد پارامترهای مدل میسر می‌شود. در حوزه آمار و دانش رایانه، مدل بیز ساده با نام‌های دیگری نظیر «بیز ساده» (Simple Bayes) و «بیز مستقل» (Independence Bayes) نیز شناخته می‌شود که در بسیاری از حوزه‌های دیگر نیز کاربرد دارد. به منظور آشنایی خوانندگان با این زمینه کاربردی بخصوص برای افرادی که به تازگی خواستار ورود به گروه «تحلیل‌گران داده» (Data Scientist) هستند، متن حاضر را تهیه کرده‌ایم.

همانطور که می‌دانید، بسیاری از روش‌های به کار گرفته شده در یادگیری ماشین، از تکنیک‌های آماری بهره می‌برند. دسته بند بیز ساده نیز همانطور که از اسمش بر می‌آید از این قاعده مستنثنی نیست. هر چند که تکنیک دسته‌بند بیز ساده از قضیه بیز به منظور تفکیک احتمالات استفاده می‌کند ولی نمی‌توان آن را یک «استنباط بیزی» (Bayesian Inference) در نظر گرفت. برای آگاهی بیشتر در زمینه مفاهیم به کار رفته در این نوشتار بهتر است مطلب قضیه بیز در احتمال شرطی و کاربردهای آن و یادگیری ماشین به زبان قضیه بیز، بی نظمی شانون و فلسفه را بخوانید. همچنین مطالعه تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده نیز خالی از لطف نیست.

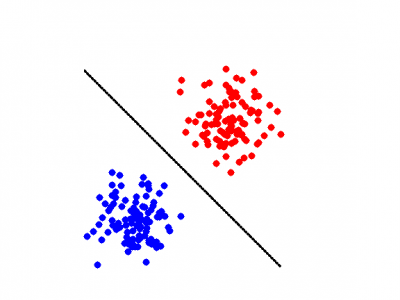
دسته‌ بند بیز ساده

اغلب به عنوان یک راهکار ساده برای دسته‌بندی و تعیین روشی برای تشخیص برچسب اشیاء یا نقاط از تکنیک دسته‌بند بیز استفاده می‌شود. برای به کارگیری دسته‌بند بیز ساده، الگوریتم یکتایی وجود ندارد در عوض خانواده‌ای از الگوریتم‌ها موجود است که با فرض استقلال ویژگی‌ها یا متغیرها نسبت به یکدیگر عمل می‌کنند. برای مثال اندازه یک میوه و رنگ آن که متغیرها مستقل در نظر گرفته می‌شوند، در تعیین نوع آن می‌توانند موثر باشند. بنابراین اگر میوه‌ای با رنگ قرمز و دارای اندازه حدود ۱۰ سانتی‌متر باشد، با احتمال زیاد سیب است.

در بیشتر تکنیک‌ها و مدل‌های بیز ساده از روش حداکثرسازی تابع درستنمایی استفاده می‌شود. هرچند تکنیک دسته‌بند بیز ساده دارای فرضیات محدود و قابل دسترس است ولی به خوبی می‌تواند از  عهده حل مسائل واقعی برآید و به عنوان یک رقیب برای روش‌های «جنگل تصادفی» (Random Forest) محسوب شود. یکی از مزایای قابل توجه در دسته‌بند بیز ساده، امکان برآورد پارامترهای مدل با اندازه نمونه کوچک به عنوان مجموعه «داده آموزشی» (Training Data) است.

دسته بند بیز و مدل احتمالاتی

بیز ساده را می‌توان یک مدل برمبنای احتمال شرطی در نظر گرفت. فرض کنید $$X=(x_1,\dots ,x_n)$$ برداری از $$n$$ ویژگی‌ را بیان کند که به صورت متغیرهای مستقل هستند. به این ترتیب می‌توان احتمال رخداد $$C_k$$ یعنی $${\displaystyle p(C_{k}\mid x_{1},\dots ,x_{n})\,}$$ را به عنوان یکی از حالت‌های کلاس رخدادهای مختلف به ازاء $$k$$های متفاوت، به شکل زیر نمایش داد.

$$\large {\displaystyle p(C_{k}\mid X )={\frac {p(C_{k})\ p(X \mid C_{k})}{p(X)}}\,}$$

رابطه ۱

همانطور که دیده می شود رابطه بالا همان قضیه بیز است. به عنوان یادآوری قضیه بیز را براساس احتمالات پیشامدهای «پیشین» (Prior)، «پسین» (Posterior)، «درستنمایی» (Likelihood) و «شواهد» (Evidence) در رابطه زیر بازنویسی می‌کنیم.

$$\large {\displaystyle {\text{posterior}}={\frac {{\text{prior}}\times {\text{likelihood}}}{\text{evidence}}}\,}$$

به این ترتیب برای محاسبه احتمال $${\displaystyle p(C_{k}\mid x_{1},\dots ,x_{n})\,}$$ کافی است از «احتمال توام» (Joint Probability) کمک بگیریم و به کمک احتمال شرطی با توجه به استقلال متغیرها، آن را ساده کنیم.

$$\large {\displaystyle {p(C_{k},x_{1},\dots ,x_{n})=p(x_{1},\dots ,x_{n},C_{k})\\=p(x_{1}\mid x_{2},\dots ,x_{n},C_{k})p(x_{2},\dots ,x_{n},C_{k})\\=p(x_{1}\mid x_{2},\dots ,x_{n},C_{k})p(x_{2}\mid x_{3},\dots ,x_{n},C_{k})p(x_{3},\dots ,x_{n},C_{k})،\\=\dots \\=p(x_{1}\mid x_{2},\dots ,x_{n},C_{k})p(x_{2}\mid x_{3},\dots ,x_{n},C_{k})\dots p(x_{n-1}\mid x_{n},C_{k})p(x_{n}\mid C_{k})p(C_{k})\\}}$$

با فرض استقلال مولفه‌ها یا ویژگی‌های $$x_i$$ها از یکدیگر می‌توان احتمالات را به شکل ساده‌تری نوشت. کافی است رابطه زیر را در نظر بگیریم.

$$\large {\displaystyle p(x_{i}\mid x_{i+1},\dots ,x_{n},C_{k})\approx p(x_{i}\mid C_{k})\,}.$$

به این ترتیب احتمال توام را به صورت حاصلضرب احتمال شرطی می‌توان نوشت.

$$\large {\displaystyle {\begin{aligned}p(C_{k}\mid x_{1},\dots ,x_{n})&\varpropto p(C_{k},x_{1},\dots ,x_{n})\\&\approx p(C_{k})\ p(x_{1}\mid C_{k})\ p(x_{2}\mid C_{k})\ p(x_{3}\mid C_{k})\ \cdots \\&=p(C_{k})\prod _{i=1}^{n}p(x_{i}\mid C_{k})\,,\end{aligned}}}$$

رابطه ۲

نکته: در رابطه ۱ مخرج کسر در همه محاسبات یکسان و ثابت است در نتیجه می‌توان احتمال شرطی را متناسب با احتمال توام در نظر گرفت. در رابطه بالا این تناسب را با علامت $$\varpropto$$ نشان داده‌ایم.

با توجه به نکته گفته شده، و رابطه ۲ می‌توانیم احتمال شرطی معرفی شده در رابطه ۱ را به صورت زیر بدست آوریم. در نتیجه احتمال تعلق یک مشاهده به دسته یا گروه $$Cـk$$ با توجه به مشاهدات $$X$$ مطابق با رابطه زیر مشخص خواهد شد.

$$\large {\displaystyle p(C_{k}\mid x_{1},\dots ,x_{n})={\frac {1}{Z}}p(C_{k})\prod _{i=1}^{n}p(x_{i}\mid C_{k})}$$

توجه داشته باشید که در اینجا احتمال شواهد (مشاهدات) به صورت  $${\displaystyle Z=p(\mathbf {x} )=\sum _{k}p(C_{k})\ p(\mathbf {x} \mid C_{k})}$$ در نظر گرفته شده است. واضح است که $$Z$$ به شواهد و مشاهدات $${\displaystyle x_{1},\dots ,x_{n}}$$ وابسته است.

ساخت دسته‌بند براساس مدل احتمالاتی

در قسمت قبل با نحوه محاسبه مدل احتمالاتی بیز آشنا شدید. اما در این بخش به کمک «قواعد تصمیم» (Decision Rule)، دسته‌بند بیز را ایجاد و کامل می‌کنیم. یکی از اساسی‌ترین قواعد تصمیم، انتخاب فرضیه محتمل‌تر است. به این ترتیب از بین تصمیمات مختلف، آن کاری را انجام می‌دهیم که براساس شواهد جمع‌آوری شده، بیشترین احتمال رخداد را دارد. این قاعده را «حداکثر پسین» (Maximum Posterior) یا به اختصار MP می‌نامند. به این ترتیب دسته بند بیز را می‌توان به صورت تابعی از تصمیمات $$C_k$$ در نظر گرفت که بوسیله تابع $$\widehat{y}$$‌ تخمین زده می‌شود.

فیلم آموزش الگوریتم بیز ساده Naive Bayes + مفاهیم و پیاده‌سازی عملی (آموزش رایگان) در فرادرس

کلیک کنید

حداکثرسازی این تابع را به صورت زیر نشان می‌دهیم.

$$\large {\displaystyle {\hat {y}}={\underset {k\in \{1,\dots ,K\}}{\operatorname {argmax} }}\ p(C_{k})\displaystyle \prod _{i=1}^{n}p(x_{i}\mid C_{k}).}$$

در نتیجه با توجه به توزیع‌های مختلفی که ممکن است نمونه تصادفی داشته باشد (نمونه از آن جامعه آمده باشد) یعنی $$p(x_i|C_k)$$ می‌توان پارامترها را محاسبه و یا برآورد کرد.

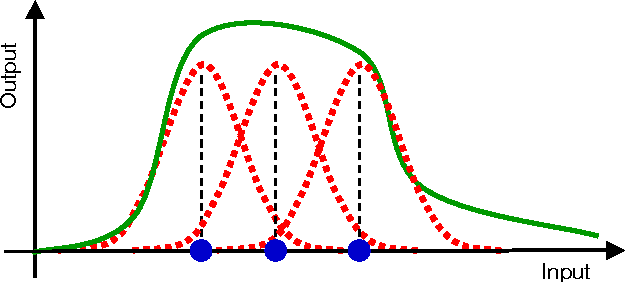
دسته بند بیز ساده گاوسی (Gaussian Naive Bayes)

اگر مشاهدات و داده‌ها از نوع پیوسته باشند، از مدل احتمالی با توزیع گاوسی یا نرمال برای متغیرهای مربوط به شواهد می‌توانید استفاده کنید. در این حالت هر دسته یا گروه دارای توزیع گاوسی است. به این ترتیب اگر $$k$$ دسته یا کلاس داشته باشیم می‌توانیم برای هر دسته میانگین و واریانس را محاسبه کرده و پارامترهای توزیع نرمال را برای آن‌ها برآورد کنیم. فرض کنید که $$\mu_k$$ میانگین و $$\sigma_k^2$$ واریانس دسته $$k$$ام یعنی $$C_k$$ باشد. همچنین $$\nu$$ را مشاهدات حاصل از متغیرهای تصادفی $$X$$ در نظر بگیرید. از آنجایی که توزیع $$X$$ در هر دسته گاوسی (نرمال) فرض شده است، خواهیم داشت:

$$\large {\displaystyle p(x=v\mid C_{k})={\frac {1}{\sqrt {2\pi \sigma _{k}^{2}}}}\,e^{-{\frac {(v-\mu _{k})^{2}}{2\sigma _{k}^{2}}}}}$$

دسته بند بیز ساده چندجمله‌ای (Multinomial Naive Bayes)

بیز ساده چندجمله‌ای، به عنوان یک دسته‌بند متنی بسیار به کار می‌آید. در این حالت برحسب مدل احتمالی یا توزیع چند جمله‌ای، برداری از $$n$$ ویژگی برای یک مشاهده به صورت $${\displaystyle X =(x_{1},\dots ,x_{n})}$$ با احتمالات  $${\displaystyle (p_{1},\dots ,p_{n})}$$ در نظر گرفته می‌شود. مشخص است که در این حالت بردار $$X$$ بیانگر تعداد مشاهداتی است که ویژگی خاصی را دارا هستند. به این ترتیب تابع درستنمایی در چنین مدلی به شکل زیر نوشته می‌شود.

$$\large {\displaystyle p(\mathbf {x} \mid C_{k})={\frac {(\sum _{i}x_{i})!}{\prod _{i}x_{i}!}}\prod _{i}{p_{ki}}^{x_{i}}}$$

اگر مدل بیز ساده را براساس لگاریتم تابع درستنمایی بنویسیم، به صورت یک دسته‌بند خطی درخواهد آمد.

$$\large {\displaystyle {\begin{aligned}\log p(C_{k}\mid \mathbf {x} )&\varpropto \log \left(p(C_{k})\prod _{i=1}^{n}{p_{ki}}^{x_{i}}\right)\\&=\log p(C_{k})+\sum _{i=1}^{n}x_{i}\cdot \log p_{ki}\\&=b+\mathbf {w} _{k}^{\top }\mathbf {x} \end{aligned}}}$$

واضح است که در این حالت $$b=\log p(C_k)$$ و $$w_{ki}=\log p_{ki}$$‌ است.

دسته بند بیز ساده برنولی (Bernoulli Naive Bayes)

در این قسمت به بررسی توزیع برنولی و دسته‌بندی بیز خواهیم پرداخت. به شکلی این نوع از دسته‌بند بیز بیشترین کاربرد را در دسته‌بندی متن‌های کوتاه داشته، به همین دلیل محبوبیت بیشتری نیز دارد. در این مدل در حالت چند متغیره، فرض بر این است که وجود یا ناموجود بودن یک ویژگی در نظر گرفته شود. برای مثال با توجه به یک لغتنامه مربوط به اصطلاحات ورزشی، متن دلخواهی مورد تجزیه و تحلیل قرار می‌گیرد و بررسی می‌شود که آیا کلمات مربوط به لغتنامه ورزشی در متن وجود دارند یا خیر. به این ترتیب مدل تابع درستنمایی متن براساس کلاس های مختلف $$C_k$$ به شکل زیر نوشته می‌شود.

$$\large {\displaystyle p(\mathbf {x} \mid C_{k})=\prod _{i=1}^{n}p_{ki}^{x_{i}}(1-p_{ki})^{(1-x_{i})}}$$

مشخص است که منظور از $$p_{ki}$$ احتمال تولید مشاهده $$x_i$$‌ از کلاس $$C_k$$‌ است.

نکته: با توجه به استقلال مشاهدات، تابع درستنمایی به صورت حاصلضرب نوشته شده است.

دسته‌بندی متن به کمک دسته‌بندی بیز ساده

در این بخش به کمک تکنیک دسته‌بند بیز، مسئله تفکیک متن‌ها را حل می‌کنیم. قرار است براساس محتویات اسناد متنی آن‌ها را در دسته‌های مشخصی جای دهیم. برای مثال نامه‌های موجود در صندوق پست الکترونیکی را به دو گروه «اصلی» (Non-Spam) و «هرزنامه» (Spam) طبقه‌بندی کنیم.

فرض کنید که احتمال اینکه کلمه $$w_i$$ از یک سند در دسته $$C$$ قرار گیرد برابر با $$p(w_i|C)$$ باشد. به این ترتیب مشخص است که این احتمال به طول سند و خصوصیات دیگر سند مرتبط نیست در نتیجه کلمات به طور تصادفی در متن توزیع شده‌اند. پس شرط استقلال وجود دارد.

احتمال اینکه یک سند مثل $$D$$ شامل همه کلمات $$w_i$$‌ از دسته یا گروه $$C$$ باشد نیز مطابق رابطه زیر محاسبه می‌شود.

$$\large {\displaystyle p(D\mid C)=\prod _{i}p(w_{i}\mid C)\,}$$

سوالی که بوسیله دسته‌بند بیز پاسخ خواهیم داد، این است که احتمال اینکه سند $$D$$ به دسته یا گروه $$C$$ تعلق داشته باشد چقدر است؟ برای پاسخ به این سوال از احتمال شرطی کمک خواهیم گرفت. یعنی می‌توانیم رابطه زیر را بنویسیم.

$$\large {\displaystyle p(D\mid C)={p(D\cap C) \over p(C)}}$$

از طرفی رابطه زیر نیز برقرار است.

$$\large {\displaystyle p(C\mid D)={p(D\cap C) \over p(D)}}$$

در نتیجه به کمک قضیه بیز می‌توانیم تساوی زیر را برحسب تابع درستنمایی بازنویسی کنیم.

$$\large {\displaystyle p(C\mid D)={\frac {p(C)\,p(D\mid C)}{p(D)}}}$$

از طرفی فرض کنید که دسته‌بندی اسناد به دو شکل قابل تصور است (اصلی و هرزنامه) در نتیجه احتمال قرارگیری سند در هر یک از این دو دسته به صورت زیر محاسبه می‌شود.

$$\large {\displaystyle p(D\mid S)=\prod _{i}p(w_{i}\mid S)\,,\;\;\;\;\;\; p(D\mid \neg S)=\prod _{i}p(w_{i}\mid \neg S)\,}$$

به کمک قضیه بیز هر یک از رابطه‌های بالا را به تساوی‌های زیر تبدیل خواهیم کرد.

$$\large {\displaystyle p(S\mid D)={p(S) \over p(D)}\,\prod _{i}p(w_{i}\mid S),\;\;\;\;\; p(\neg S\mid D)={p(\neg S) \over p(D)}\,\prod _{i}p(w_{i}\mid \neg S)}$$

حال نسبت این دو احتمال (بخت) را به شکل زیر خواهیم نوشت.

$$\large {\displaystyle {p(S\mid D) \over p(\neg S\mid D)}={p(S) \over p(\neg S)}\,\prod _{i}{p(w_{i}\mid S) \over p(w_{i}\mid \neg S)}}$$

نکته: با توجه به اینکه فقط دو کلاس $$S$$ و $$\neg S$$‌ موجود بوده و البته جدا از هم نیز هستند، براساس قضیه‌های احتمال، می‌دانیم $$P(S\mid D)+P(\neg S\mid D)=1$$

با لگاریتم گرفتن از دو طرف رابطه بالا، نسبت بخت به صورت یک رابطه خطی از بخت‌ها و تابع درستنمایی در خواهد آمد. در نتیجه هرگاه مقدار $$p(S|D) > p(\neg S|D)$$ باشد سند متعلق به دسته $$S$$ است. در حقیقت کافی است محاسبه سمت راست مربوط به رابطه بالا را محاسبه کنیم. هر گاه این محاسبه مقداری مثبت داشته باشد متوجه می‌شویم که کسر سمت چپ مثبت است پس صورت بزرگتر از مخرج است. در نتیجه طبق قاعده تصمیم، حکم به تعلق سند $$D$$ به گروه $$S$$ خواهیم داد و برعکس یعنی با منفی شدن این محاسبه، تصمیم می‌گیریم که سند $$D$$ را در گروه $$\neg S$$ قرار دهیم.

همانطور که دیده شد، دسته‌بند بیز ساده به کمک قضیه بیز و تابع درستنمایی، براساس شواهد یا نمونه تصادفی تهیه شده و کلاس‌هایی که از قبل مشخص شده‌اند، سعی در طبقه‌بندی و دسته‌بندی مشاهدات در آن گروه‌ها را دارد. البته شیوه انجام این کار براساس احتمالات است در نتیجه بطور حتم دارای خطا نیز هست. بنابراین باید به کمک معیارهای ارزیابی نتایج دسته‌بندی، خطای مدل را مثلا براساس اعتبار سنجی متقابل محاسبه و اعلام کرد. البته ذکر این نکته نیز ضروری است که روش‌های دیگر دسته‌بندی مانند رگرسیون لجستیک نیز قادر به تفکیک مشاهدات به دسته‌های مشخص شده هستند.

اگر مطلب بالا برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های تصویر و پردازش سیگنال
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های برنامه‌نویسی پایتون
• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده

^^