پیش تنش و پیش کرنش در سازه های نامعین استاتیکی – از صفر تا صد

اعمال بارهای خارجی بر روی یک سازه باعث ایجاد تنش و کرنش می‌شود. عوامل دیگری نظیر «اثرات حرارتی» (Thermal Effects) حاصل از تغییرات دما، «میس‌فیت» (Misfit) ناشی از عیب و نقص‌های سازه، «پیش‌کرنش» (Prestrain) ایجاد شده توسط تغییر شکل‌های اولیه، نشست یا حرکت تکیه‌گاه‌های سازه، بارهای اینرسی ناشی از حرکت شتاب‌دار و پدیده‌های طبیعی مانند زلزله نیز می‌توانند باعث ایجاد تنش و کرنش درون سازه‌ها شوند. اثرات حرارتی، عدم تطابق‌ها و پیش‌کرنش‌ها از موارد رایج در سیستم‌های مکانیکی و ساختمانی به شمار می‌روند. به علاوه، اهمیت این موارد در طراحی سازه‌های نامعین استاتیکی بیشتر از طراحی سازه‌های معین استاتیکی است. در مبحث «تاثیر تغییر دما روی تغییر طول سازه‌ها»، به بررسی اثرات حرارتی پرداختیم. در این مقاله شما را با مفاهیم میس‌فیت، پیش‌کرنش و پیش‌تنش آشنا خواهیم کرد. در انتها، علاوه بر معرفی پیچ‌ها و مهارکش‌ها (به عنوان قطعات مورد استفاده برای تغییر طول سازه)، نحوه تحلیل سازه‌های متشکل از این قطعات را نیز توضیح خواهیم داد.

پیش‌کرنش و میس‌فیت

فرض کنید که در طی فرآیند تولید قطعات، یکی از عضوهای سازه با طولی متفاوت نسبت به مقدار از پیش تعیین شده ساخته شود. در این شرایط، عضو مذکور به خوبی درون سازه قرار نخواهد گرفت و هندسه سازه با طراحی‌های صورت گرفته تفاوت خواهد داشت. به این وضعیت، عدم تطابق یا اصطلاحاً «میس‌فیت» (Misfit) گفته می‌شود. در برخی از موارد، ایجاد میس‌فیت به صورت عمدی و به منظور به وجود آوردن کرنش در هنگام ساخت سازه صورت می‌گیرد.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

به کرنش‌های حاصل از میس‌فیت، «پیش‌کرنش» (Prestrain) گفته می‌شود؛ چراکه پیش از اعمال هرگونه بارگذاری، این کرنش‌ها درون سازه وجود دارند. به همراه پیش‌کرنش، «پیش‌تنش» (Prestress) نیز به وجود می‌آید. معمولاً به سازه‌های دارای این شرایط، «پیش‌تنیده» (Prestressed) می‌گویند. پره چرخ‌های دوچرخه، صفحات پیش‌کشیده راکت‌های تنیس، قطعات انقباضی یا اصطلاحاً «شرینک فیت» (Shrink Fit) در دستگاه‌های مختلف و تیرهای بتنی پیش‌تنیده از مثال‌های رایج در مبحث کاربرد پیش‌کرنش هستند.

اگر سازه‌ای از نظر استاتیکی معین باشد، وجود میس‌فیت‌های کوچک در یک یا چند عضو آن باعث ایجاد کرنش یا تنش نخواهد شد. با این وجود، هندسه سازه در این شرایط با طراحی‌های صورت گرفته تفاوت خواهد داشت. برای درک بهتر این موضوع، سازه نمایش داده شده در شکل زیر را در نظر بگیرید. این سازه از یک تیر افقی (AB) و یک میله عمودی (CD) تشکیل شده است. میله CD نقش نگهدارنده تیر AB را بازی می‌کند.

در صورتی که طول CD دقیقاً برابر با L باشد، AB در لحظه اتمام ساخت سازه به صورت کاملاً افقی خواهد بود. از سوی دیگر، اگر طول میله کمی بیشتر از مقدارِ از پیش تعیین شده باشد، زاویه کوچکی بین تیر و راستای افق به وجود خواهد آمد. اگرچه،  هیچ تنش یا کرنشی به دلیل طول نادرست میله درون سازه ایجاد نمی‌شود. علاوه بر این، در صورت اعمال بار P بر انتهای تیر، تنش‌های حاصل از بارگذاری به دلیل طول نادرست CD بی‌اثر خواهند شد.

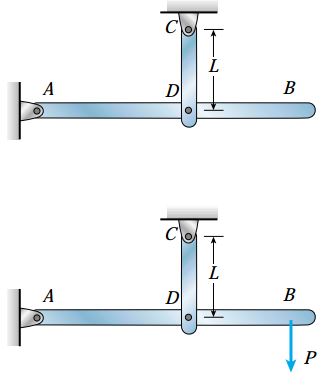
به طور کلی، اگر سازه‌ای از نظر استاتیکی معین باشد، حضور میس‌فیت‌های کوچک هیچ تأثیری بر روی ایجاد تنش و کرنش نخواهد داشت اما باعث به وجود آمدن تغییرات جزئی در هندسه سازه خواهد شد. بنابراین، تأثیر میس‌فیت بر روی یک سازه معین استاتیکی مشابه تأثیر تغییرات دما بر روی این نوع سازه است. برای سازه‌های نامعین استاتیکی، شرایط کاملاً متفاوت خواهد بود. در این سازه‌ها، فضای کافی برای تغییر و تعدیل میس‌فیت‌ها وجود ندارد.

برای درک بهتر این موضوع، سازه زیر را در نظر بگیرید. در این سازه، یک تیر افقی توسط دو میله عمودی نگهداری می‌شود. در صورتی که طول هر دو میله دقیقاً برابر با L باشد، تیر AB در لحظه اتمام ساخت سازه به صورت کاملاً افقی خواهد بود و هیچ تنش یا کرنشی درون سازه وجود نخواهد داشت.

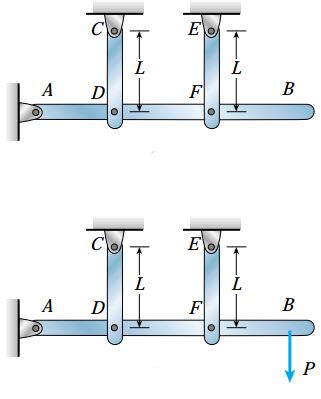
فرض کنید طول میله CD کمی بیشتر از مقدارِ از پیش تعیین شده باشد. در این شرایط، به منظور مونتاژ سازه باید با اعمال نیروهای خارجی، CD را تحت فشار یا EF را تحت کشش قرار داد. پس از قرارگیری میله‌ها در محل مناسب، باید اعمال نیروهای خارجی را متوقف کرد.

با اتمام این فرآیند، تیر تغییر شکل می‌دهد و دوران می‌کند. به علاوه، میله CD تحت فشار و میله EF تحت کشش قرار می‌گیرد. به عبارت دیگر، در تمام عضوها پیش‌کرنش به وجود می‌آید و سازه پیش‌تنیده می‌شود (بدون اعمال بارهای خارجی). به این ترتیب، در صورت اعمال بار P به انتهای تیر، تنش و کرنش‌های بیشتری در سازه رخ می‌دهند.

روند کلی تحلیل یک سازه نامعین استاتیکی در هنگام وجود میس‌فیت و پیش‌کرنش مشابه روش‌های ارائه شده در مباحث «سازه‌های نامعین استاتیکی» و «تاثیر تغییر دما روی تغییر طول سازه‌ها» است. این روند شامل استفاده از معادله تعادل، معادله سازگاری، روابط نیرو-جابجایی و روابط دما-جابجایی می‌شود. برای آشنایی بیشتر با روش‌های موجود، به مثال انتهای مقاله مراجعه کنید.

پیچ و مهارکِش

به منظور ایجاد پیش‌تنش در یک سازه باید برخی از قطعه‌های به کار رفته در آن را نسبت به طول تئوری‌شان تحت فشار یا کشش قرار داد. یکی از روش‌های ساده برای انجام این کار، استفاده از پیچ یا مهارکِش (پیچ تنظیم دوطرفه) است.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

در پیچ‌ها، چرخش مهره باعث حرکت آن در امتداد پیچ می‌شود (شکل زیر). با توجه به پیکربندی سازه، چرخاندن مهره می‌تواند باعث کشیدگی یا فشردگی یک عضو شود. میزان حرکت مهره به ازای هر چرخش برابر با فاصله بین آج‌ها (گام آج) است.

جابجایی مهره در امتداد پیچ از رابطه زیر به دست می‌آید:

δ: جابجایی کل؛ n: تعداد چرخش‌های کامل (این عدد لزوماً یک عدد صحیح نیست)؛ p: گام آج (فاصله بین آج‌های پیچ)

در مهارکش‌ها، از دو پیچ انتهایی استفاده می‌شود. به دلیل وجود یک پیچ راست‌گرد در یک سمت و یک پیچ چپ‌گرد در سمت دیگر، افزایش یا کاهش طول در اثر چرخشِ قلابِ میانی رخ می‌دهد (شکل زیر).

یک چرخش کامل قلاب، آن را به اندازه یک گام آج (p) در راستای پیچ‌ها جابجا می‌کند. بنابراین، در صورت محکم کردن بست با یک چرخش، پیچ‌ها به اندازه 2p به یکدیگر نزدیک‌تر و بست نیز به اندازه 2p کوتاه‌تر می‌شود. به این ترتیب، جابجایی کل از رابطه زیر به دست می‌آید:

مهارکشِ‌ها معمولاً در کابل‌ها و به منظور ایجاد کشش اولیه در آن‌ها مورد استفاده قرار می‌گیرند.

مثال

شکل زیر، مجموعه‌ای متشکل از یک لوله مسی، یک صفحه انتهایی صلب و دو کابل فولادی دارای مهارکش را نمایش می‌دهد. با چرخاندن قلاب مهارکش‌ها، کابل‌ها از حالت سستی درمی‌آیند.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

چرخاندن قلاب‌ها تا لحظه چِفت شدن مجموعه (بدون ایجاد تنش‌های اولیه) ادامه می‌یابد. (توجه داشته باشید که در صورت چرخاندن بیشتر قلاب، شرایط پیش‌تنیده در کابل‌ها به وجود می‌آید. در این شرایط، کابل‌ها تحت کشش و لوله تحت فشار قرار می‌گیرند.)

• الف) با n بار چرخاندن قلاب مهارکش‌ها، میزان نیروهای به وجود آمده درون کابل‌ها و لوله چقدر خواهد بود؟
• ب) میزان کاهش طول لوله چقدر خواهد بود؟

تحلیل این مسئله را با حذف صفحه موجود در انتهای راست مجموعه شروع می‌کنیم. با این کار، امکان تغییر طول آزادانه برای لوله و کابل‌ها فراهم می‌شود (شکل زیر).

با n بار چرخاندن قلاب مهارکش‌ها، طول کابل‌ها به اندازه δ₁ تغییر می‌کند:

نیروهای کششی موجود در کابل‌ها و نیروهای فشاری موجود در لوله باید به گونه‌ای باشند که با افزایش طول کابل‌ها و کاهش طول لوله، طول نهایی تمام قطعات با یکدیگر برابر شود. در شکل زیر، نیروی کششی در کابل‌های فولادی با P_s و نیروی فشاری در لوله مسی با P_c نمایش داده شده است.

میزان تغییر طول کابل بر اثر اعمال نیروی P_s از رابطه زیر به دست می‌آید:

E_sA_s: صلبیت محوری کابل؛ L: طول کابل

میزان تغییر طول لوله بر اثر اعمال P_c نیز از طریق رابطه زیر تعیین می‌شود:

E_cA_c: صلبیت محوری لوله

روابط δ₂ و δ₃، روابط بار-جابجایی هستند. کاهش طول نهایی هر یک از کابل‌ها با اختلاف بین کاهش طول ناشی از چرخاندن قلاب مهارکش (δ₁) و افزایش طول ناشی از نیروی داخلی (δ₂) برابر است. به این ترتیب، کاهش طول نهایی کابل باید با کاهش طول لوله (δ₃) برابر باشد:

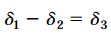
معادله بالا، معادله سازگاری است. با جایگذاری رابطه δ₁=np و روابط بار-جابجایی در معادله سازگاری، خواهیم داشت:

با بازنویسی معادله بالا داریم:

معادله بالا، فرم اصلاح‌شده معادله سازگاری است. شکل زیر، نمودار جسم آزاد مجموعه مورد تحلیل، پس از حذف صفحه سمت راست را نشان می‌دهد.

با توجه به نمودار جسم آزاد، معادله تعادل به صورت زیر خواهد بود:

الف) نیروهای موجود در کابل‌ها و لوله

با حل هم‌زمان فرم اصلاح‌شده معادله سازگاری و معادله تعادل، نیروهای محوری درون کابل‌های فولادی و لوله مسی به صورت زیر تعیین می‌شوند:

به خاطر داشته باشید که نیروهای P_s به صورت کششی و نیروی P_c به صورت فشاری هستند. در صورت تمایل محاسبه تنش‌های موجود در کابل و لوله (σ_s و σ_c) می‌توانید مقادیر نیروهای مربوط به هر یک را بر مساحتشان (A_s و A_c) تقسیم کنید.

ب) کاهش طول لوله

کاهش طول لوله با کمیت δ₃ برابر است. با جایگذاری فرمول‌های به دست آمده در رابطه δ₃ خواهیم داشت:

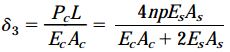
با استفاده از فرمول‌های به دست آمده می‌توانیم مقادیر نیرو، تنش و جابجایی مجموعه را به سادگی محاسبه کنیم.

^^