تاثیر تغییر دما روی تغییر طول سازه ها – آموزش جامع

اعمال بارهای خارجی بر روی یک سازه باعث ایجاد تنش و کرنش درون آن می‌شود. با این وجود، عوامل دیگری نظیر «اثرات حرارتی» (Thermal Effects) حاصل از تغییرات دما، «عدم تطابق» (Misfit) ناشی از عیب و نقص‌های سازه، «پیش‌کرنش» (Prestrain) ایجاد شده توسط تغییر شکل‌های اولیه، نشست یا حرکت تکیه‌گاه‌های سازه، بارهای اینرسی ناشی از حرکت شتاب‌دار و پدیده‌های طبیعی مانند زلزله نیز می‌توانند باعث ایجاد تنش و کرنش درون سازه‌ها شوند. اثرات حرارتی، عدم تطابق‌ها و پیش‌کرنش‌ها از موارد رایج در سیستم‌های مکانیکی و ساختمانی به شمار می‌روند. به علاوه، اهمیت این موارد در طراحی سازه‌های نامعین استاتیکی بیشتر از طراحی سازه‌های معین استاتیکی است. در این مقاله، تاثیر تغییر دما بر روی تغییر شکل سازه‌های نامعین استاتیکی را مورد ارزیابی قرار خواهیم داد. در انتها، به منظور آشنایی با نحوه تحلیل این نوع سازه‌ها در بارگذاری‌های حرارتی، چند مثال را برای شما تشریح خواهیم کرد.

اثرات حرارتی

تغییر دمای سازه باعث انبساط یا انقباض مواد تشکیل‌دهنده و ایجاد «تنش حرارتی» (Thermal Stress) و «کرنش حرارتی» (Thermal Strain) در آن می‌شود. شکل زیر،  نمونه ساده‌ای از انبساط حرارتی یک بلوک را نمایش می‌دهد. صفحات این بلوک تحت هیچ محدودیتی قرار ندارند و می‌توانند آزادانه حرکت پیدا کنند. با افزایش دمای بلوک، المان‌های تشکیل‌دهنده آن در راستای تمام جهات با کرنش‌های حرارتی مواجه می‌شوند. به این ترتیب، ابعاد بلوک افزایش می‌یابد. اگر گوشه A را به عنوان یک نقطه مرجع (ثابت) در نظر بگیریم و بگذاریم ضلع AB راستای اصلی خود را حفظ کند، شکل بلوک مطابق خط‌چین‌های نمایش داده شده در شکل زیر تغییر خواهد کرد.

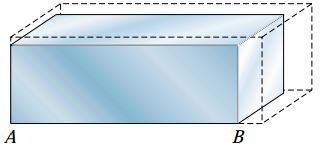
در اکثر مواد، میزان کرنش حرارتی ε_T با تغییرات دما ΔT متناسب است:

کمیت α، یکی از خواص ماده موسوم به «ضریب انبساط حرارتی» (Coefficient of Thermal Expansion) است. به دلیل بی‌بعد بودن کمیت کرنش، واحد ضریب انبساط حرارتی برابر با معکوس واحد دما در نظر گرفته می‌شود. در سیستم SI می‌توان α را با یکی از واحدهای معکوس کلوین یا معکوس درجه سلسیوس بیان کرد. به دلیل برابر بودن اختلاف دما در هر دو واحد کلوین و درجه سلسیوس، مقدار α در هر دو حالت یکسان خواهد بود. در سیستم واحدهای آمریکایی، α بر حسب معکوس فارنهایت بیان می‌شود. به عنوان یک قاعده کلی در نظر داشته باشید که در هنگام محاسبه کرنش‌های حرارتی، معمولاً علامت مثبت برای انبساط و علامت منفی برای انقباض مورد استفاده قرار می‌گیرد.

برای نمایش اهمیت کرنش‌های حرارتی، آن‌ها را با کرنش‌های ناشی از اعمال بار مقایسه می‌کنیم. یک میله تحت بار محوری با کرنش طولی ε=σ/E را در نظر بگیرید (σ، تنش و E، مدول الاستیسیته میله را نمایش می‌دهد). سپس، فرض کنید که یک میله مشابه دیگر در معرض تغییر دمای ΔT و کرنش حرارتی ε=αΔT قرار گرفته است. با برابر قرار دادن این دو کرنش، معادله زیر حاصل می‌شود:

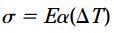
σ، تنش محوری مورد نیاز برای ایجاد کرنشی برابر با کرنش حاصل از تغییر دمای ΔT را نمایش می‌دهد. به عنوان مثال، یک میله فولادی ضد زنگ با مدول الاستیسیته E=30x10⁶psi و ضریب انبساط گرمایی α=9.6x10^-6/F را در نظر بگیرید. با قرار دادن این مقادیر در معادله بالا می‌توان مشاهده کرد که اگر دمای میله را به اندازه 100 درجه فارنهایت تغییر دهیم، میزان کرنش حرارتی با کرنش ناشی از اعمال تنش 29000 پوند بر اینچ مربعی برابر خواهد بود. این میزان تنش در محدوده تنش‌های مجاز برای فولاد ضد زنگ قرار دارد. به این ترتیب، تغییرات نسبتاً کوچک دما می‌توانند به اندازه بارهای معمولی باعث ایجاد کرنش درون سازه شوند. این مسئله، اهمیت تأثیر دما بر روی طراحی‌های مهندسی را نمایش می‌دهد.

مواد ساختمانی در هنگام افزایش دما، منبسط و هنگام کاهش دما، منقبض می‌شوند. به این ترتیب، علامت کرنش حرارتی در حین افزایش دما مثبت است. کرنش‌های حرارتی معمولاً برگشت‌پذیر هستند. بنابراین در صورت بازگشت دما به مقدار اولیه، شکل عضوهای سازه نیز به حالت اولیه خود بازمی‌گردد. با این وجود، تعداد کمی از آلیاژهای فلزی جدید از این رفتار پیروی نمی‌کنند. در این مواد خاص، افزایش دما باعث کاهش ابعاد و کاهش دما باعث افزایش ابعاد سازه می‌شود. رفتار آب از نقطه نظر حرارتی به عنوان یکی از موارد خاص به شمار می‌رود. نکته غیر معمول در مورد آب این است که پس از رسیدن به دمای 4 درجه سلسیوس،  افزایش و کاهش دما باعث افزایش حجم ماده می‌شوند. در نتیجه، حداکثر چگالی آب در دمای 4 درجه سلسیوس رخ می‌دهد.

اکنون بلوک زیر را در نظر بگیرید. فرض می‌کنیم که ماده تشکیل‌دهنده این بلوک، همگن و همسانگرد است. به علاوه، افزایش دمای ΔT نیز به صورت یکنواخت درون بلوک ایجاد می‌شود. با در نظر گرفتن این فرضیات می‌توانیم میزان افزایش ابعاد بلوک را با ضرب طول اولیه در کرنش حرارتی محاسبه کنیم.

به عنوان مثال، اگر یکی از ابعاد بلوک برابر L باشد، میزان افزایش این بعد با استفاده از رابطه زیر به دست می‌آید:

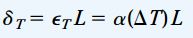
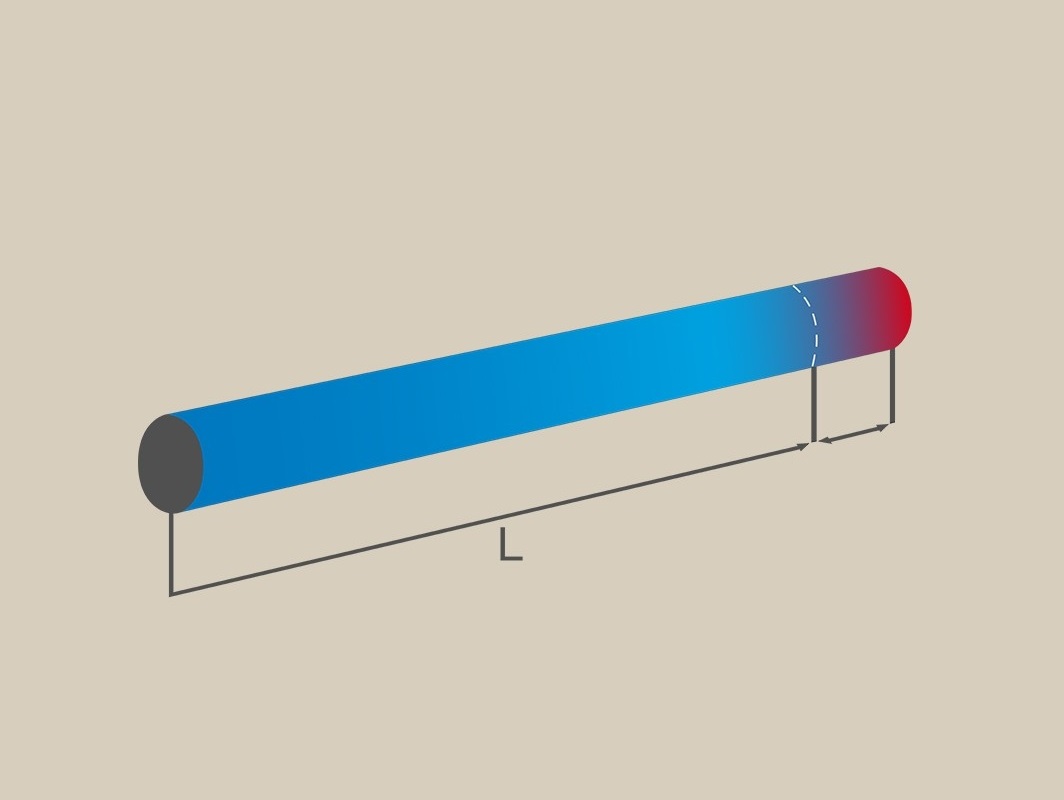
این رابطه، یک رابطه دما-جابجایی و معادلِ رابطه نیرو-جابجایی در مبحث «تحلیل سازه‌های نامعین استاتیکی» است. به منظور محاسبه تغییر طول عضوهایی که تحت تغییرات یکنواخت دما قرار گرفته‌اند می‌توان از رابطه دما-جابجایی استفاده کرد. شکل زیر، نمونه‌ای از افزایش طول δ_T ناشی تغییرات یکنواخت دما در یک میله منشوری را نمایش می‌دهد. (توجه داشته باشید که بعد جانبی میله نیز در اثر افزایش دما تغییر می‌کند اما به دلیل عدم تأثیر این تغییرات بر روی انتقال بارهای محوری توسط میله، از نمایش آن‌ها بر روی شکل صرف نظر شده است.)

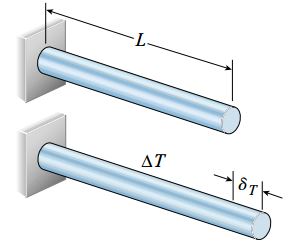
در بخش‌های قبلی فرض کردیم که هیچ عامل محدودکننده‌ای برای انبساط یا انقباض سازه وجود ندارد. این شرایط برای اجسام ساکن بر روی یک سطح بدون اصطکاک یا اجسام آویزان در فضای باز صدق می‌کند. در این موارد، بر اثر تغییرات یکنواخت دما هیچ تنشی درون شی رخ نمی‌دهد. با این وجود، تغییرات غیر یکنواخت دما می‌توانند باعث ایجاد تنش‌های داخلی شوند. تکیه‌گاه‌های موجود در اکثر سازه‌ها از انبساط یا انقباض آزادانه جلوگیری می‌کنند. در این موارد، تغییرات یکنواخت دما نیز منجر به گسترش تنش‌های حرارتی درون سازه می‌شوند.

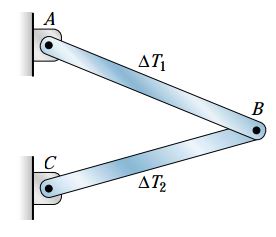
برای آشنایی با پیامدهای اثرات حرارتی، خرپای نمایش داده شده در شکل زیر را در نظر بگیرید. سپس، فرض کنید که دمای میله AB به اندازه ΔT₁ و دمای میله BC به اندازه ΔT₂ تغییر می‌کند. این سازه از نظر استاتیکی معین است. بنابراین، امکان افزایش یا کاهش طول آزادانه هر دو میله و در نتیجه جابجایی مفصل B وجود دارد. در این حالت، هیچ تنشی در میله‌ها و هیچ عکس‌العملی در تکیه‌گاه‌ها رخ نمی‌دهد. در سازه‌های معین استاتیکی، تغییرات یکنواخت دما باعث ایجاد کرنش‌های حرارتی و تغییر طول عضوهای سازه می‌شوند اما هیچ تنشی در این فرآیند به وجود نمی‌آید.

در سازه‌های نامعین استاتیکی شرایط متفاوت است. در این سازه‌ها، ایجاد تنش‌های حرارتی به مواد تشکیل‌دهنده و ماهیت تغییرات دما بستگی دارد. برای آشنایی با سناریوهای مختلف، سازه نمایش داده شده در شکل زیر را در نظر بگیرید. به دلیل فراهم بودن امکان حرکت افقی در مفصل D، هیچ تنشی در هنگام افزایش یکنواخت دمای خرپا به وجود نمی‌آید. در این شرایط، طول تمام عضوهای سازه متناسب با طول اولیه خود افزایش می‌یابد و اندازه خرپا کمی بزرگ‌تر می‌شود.

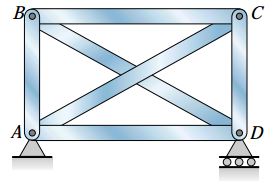
اگر افزایش دما تنها بر روی برخی از میله‌ها اعمال شود، آرایش نامعین استاتیکی میله‌ها از انبساط آزادانه سازه جلوگیری می‌کند و باعث ایجاد تنش‌های حرارتی درون سازه می‌شود. برای تصور این وضعیت، فرض کنید که تنها دمای یکی از میله‌ها افزایش یافته است. با افزایش طول این میله، میله‌های دیگر در برابر تغییرات آن مقاومت می‌کنند و باعث ایجاد تنش در تمام عضوهای سازه می‌شوند. تحلیل یک سازه نامعین استاتیکی در هنگام وجود تغییرات دما بر اساس مفاهیم معادلات تعادل، معادلات سازگاری و روابط جابجایی صورت می‌گیرد. تفاوت اصلی در این تحلیل‌ها، استفاده از روابط دما-جابجایی به همراه روابط نیرو-جابجایی (δ=PL/AE) برای حل مسئله است.

مثال‌های کاربردی

به منظور آشنایی با جزئیات فرآیند تحلیل سازه‌های نامعین استاتیکی در هنگام وجود تغییرات دما، به تشریح دو مثال کاربردی می‌پردازیم.

مثال 1

در شکل زیر، یک میله منشوری با طول L بین دو تکیه‌گاه ثابت نمایش داده شده است. اگر دمای میله به اندازه ΔT و به طور یکنواخت افزایش یابد، میزان تنش حرارتی ایجاد شده σ_T در آن چقدر خواهد بود؟ (ماده تشکیل‌دهنده میله را الاستیک خطی در نظر بگیرید.)

با افزایش دما، میله به سمت افزایش طول تمایل پیدا می‌کند. به دلیل محدود بودن دو انتهای A و B، عکس‌العمل‌های R_A و R_B در تکیه‌گاه‌های میله ایجاد می‌شوند. در این شرایط، میله تحت تنش‌های فشاری یکنواخت قرار می‌گیرد.

معادله تعادل

تنها نیروهای اعمال شده بر روی میله، عکس‌العمل‌های تکیه‌گاهی هستند. بنابراین، تعادل نیروها در راستای عمودی به صورت زیر خواهد بود:

به دلیل وجود تنها یک معادله و دو مجهول، سازه مورد بررسی از نظر استاتیکی نامعین محسوب می‌شود. از این‌رو باید به سراغ معادلات دیگر برویم.

معادله سازگاری

به دلیل ثابت بودن تکیه‌گاه‌ها، تغییر طول میله برابر با صفر خواهد بود. بنابراین:

به منظور تعیین این تغییر طول، تکیه‌گاه بالایی میله را مطابق شکل زیر حذف می‌کنیم. به این ترتیب، میله در انتهای پایینی خود ثابت می‌ماند و از انتهای بالایی خود آزادانه جابجا می‌شود.

اگر تنها نیروی اعمال شده از طرف تغییرات دما باشد، میله به اندازه δ_T افزایش طول می‌دهد. در صورت اعمال نیروی R_A نیز طول میله به اندازه δ_R کاهش می‌یابد. بنابراین، تغییر طول کلی میله برابر با δ_AB=δ_T-δ_R خواهد بود. در نتیجه، معادله سازگاری به صورت زیر نوشته می‌شود:

روابط جابجایی

افزایش طول میله بر اثر تغییر دما با استفاده از رابطه دما-جابجایی تعیین می‌شود:

α: ضریب انبساط حرارتی

کاهش طول ناشی از اعمال نیروی R_A نیز با استفاده از رابطه نیرو-جابجایی به دست می‌آید:

E: مدول الاستیسیته؛ A: مساحت سطح مقطع میله

حل معادلات به دست آمده

با جایگذاری روابط جابجایی در معادله سازگاری، معادله زیر حاصل می‌شود:

با حل هم‌زمان معادله بالا و معادله تعادل نسبت به R_A و R_B خواهیم داشت:

با توجه به این رابطه، تنش حرارتی درون میله برابر است با:

در هنگام افزایش دمای میله، این تنش به صورت فشاری خواهد بود.

نکته اول

در این مثال، مقدار عکس‌العمل‌های تکیه‌گاهی مستقل از طول میله و مقدار تنش نیز مستقل از طول و مساحت سطح مقطع بود. در واقع، یکی از مزیت‌های راه حل‌های پارامتری، مشاهده نحوه تاثیر پارامترهای مختلف بر روی یکدیگر است. در صورت ارائه یک مثال کاملاً عددی نمی‌توانستیم ویژگی‌های مهم در رفتار میله را به خوبی تشخیص دهیم.

نکته دوم

به منظور تعیین تغییر طول حرارتی، ماده را به صورت همگن و افزایش دما در درون میله را به صورت یکنواخت در نظر گرفتیم. برای تعیین تغییر طول ناشی از نیروی عکس‌العمل نیز رفتار ماده را به صورت الاستیک خطی فرض کردیم. در هنگام استفاده از روابط δ_T و δ_R باید همیشه محدودیت و فرضیات مذکور را در نظر داشته باشیم.

نکته سوم

برای این مثال، جابجایی طولی میله نه‌تنها در تکیه‌گاه‌ها بلکه در تمام سطح مقطع‌ها برابر با صفر بود. به این ترتیب، هیچ کرنش محوری در این میله رخ نداد. به این شرایط خاص، وجود تنش‌های طولی به همراه عدم وجود کرنش‌های طولی گفته می‌شود. به خاطر داشته باشید که در این شرایط، اعمال فشار محوری و همچنین تغییرات دما باعث به وجود آمدن کرنش‌های عرضی در میله خواهند شد. با این وجود، این نوع کرنش تاثیری بر روی نحوه انتقال بار نخواهد داشت.

مثال 2

پوششی به شکل یک لوله دایره‌ای با طول L را در نظر بگیرید. این پوشش مطابق شکل زیر در اطراف یک پیچ و بین دو واشر قرار گرفته و مهره انتهای پیچ تا لحظه چِفت شدن پوشش در میان واشرها چرخانده شده است. جنس مواد تشکیل‌دهنده پوشش و پیچ با یکدیگر تفاوت دارند. (ضریب انبساط حرارتی پوشش (α_S) را بزرگ‌تر از ضریب انبساط حرارتی پیچ (α_B) در نظر بگیرید.)

• الف) اگر دمای کل مجموعه به اندازه ΔT افزایش یابد، مقدار تنش‌های توسعه‌یافته در پوشش و پیچ چقدر خواهد بود؟
• ب) مقدار افزایش طول پوشش و پیچ چقدر است؟

در صورت فراهم بودن امکان تغییر شکل آزادانه قطعات، میزان تغییر طول پوشش و پیچ به دلیل متفاوت بودن مواد تشکیل‌دهنده آن‌ها متفاوت خواهد بود. اگرچه، هنگامی که این قطعات به صورت یک مجموعه در کنار هم قرار گیرند، امکان تغییر شکل آزادانه برای آن‌ها وجود ندارد. در نتیجه، تنش‌های حرارتی در هر دو ماده گسترش می‌یابند. به منظور تعیین این تنش‌ها باید مانند تمام تحلیل‌های نامعین استاتیکی از معادلات تعادل، معادلات سازگاری و روابط جابجایی استفاده کنیم. برای به دست آوردن معادلات مورد نیاز باید قطعات سازه را از یکدیگر جدا کنیم. یک روش ساده برای این کار، حذف سرِ پیچ و فراهم کردن امکان افزایش طول آزادانه پوشش و پیچ بر اثر تغییر دمای ΔT است.

برآیند تغییر طول پوشش با δ₁ و تغییر طول پیچ با δ₂ نمایش داده می‌شود. روابط دما-جابجایی مربوط به هر یک عبارت است از:

از آنجایی که α_S بزرگ‌تر از α_B است، تغییر طول δ₁ نیز بزرگ‌تر از δ₂ خواهد بود. بنابراین، نیروهای محوری باید به گونه‌ای باشند که با کاهش طول پوشش (نیروی فشاری) و افزایش طول پیچ (نیروی کششی)، طول نهایی این قطعات با یکدیگر برابر شود. در شکل زیر، نیروی فشاری درون پوشش با P_S و نیروی کششی درون پیچ با P_B نمایش داده شده است.

نیروهای P_S و P_B به ترتیب باعث ایجاد کاهش طول پوشش (δ₃) و افزایش طول پیچ (δ₄) می‌شوند:

E_SA_S و E_BA_B، صلبیت محوری مربوط هر یک از قطعات است. معادلات بالا، روابط بار-جابجایی این مسئله را نمایش می‌دهند. تغییر طول نهایی (δ) پوشش و پیچ یکسان خواهد بود. با در نظر گرفتن این نکته می‌توانیم معادله سازگاری این مسئله را به دست بیاوریم. با توجه به شکل بالا، تغییر طول پوشش برابر با δ₁-δ₃ و تغییر طول پیچ برابر با δ₂+δ₄ است. به این ترتیب، داریم:

با جایگذاری روابط دما-جابجایی و بار-جابجایی در رابطه بالا به معادله زیر می‌رسیم:

با مرتب کردن معادله بالا خواهیم داشت:

این معادله، فرم اصلاح‌شده معادله سازگاری است. توجه داشته باشید که نیروهای P_S و P_B به عنوان مجهولات مسئله در این معادله حضور دارند. شکل زیر را می‌توان به عنوان نمودار جسم آزاد مجموعه، پس از حذف کردن سر پیچ در نظر گرفت. با استفاده از این شکل می‌توانیم معادله تعادل مسئله را به دست بیاوریم.

برای به دست آوردن معادله تعادل، نیروهای موجود در راستای افقی را با هم جمع می‌کنیم. با توجه به تعادل جسم آزاد، داریم:

این معادله نشان می‌دهد که نیروی فشاری موجود در پوشش با نیروی کششی موجود در پیچ برابر است. با حل هم‌زمان فرم اصلاح‌شده معادله سازگاری و معادله تعادل، نیروهای محوری درون پوشش و پیچ تعیین می‌شوند:

توجه: برای دستیابی به معادله بالا، فرض کردیم که دمای مجموعه افزایش می‌یابد و ضریب α_S از α_B بزرگ‌تر است. در این شرایط، P_S به عنوان نیروی فشاری درون پوشش و P_B به عنوان نیروی کششی درون پیچ در نظر گرفته می‌شود. اگر دمای مجموعه افزایش پیدا کند اما ضریب α_S کوچک‌تر از α_B باشد، نتیجه به دست آمده کاملاً متفاوت خواهد بود. در این شرایط، با افزایش دما یک فضای خالی بین سر پیچ و پوشش به وجود می‌آید. به همین دلیل، هیچ تنشی در هیچ‌یک از بخش‌های مجموعه ایجاد نمی‌شود.

الف) تعیین تنش‌های موجود در پوشش و پیچ

تنش‌های موجود در پوشش (σ_S) و پیچ (σ_B) با استفاده از نیروهای به دست آمده در بخش‌های قبلی و مساحت هر یک از قطعات تعیین می‌شوند:

با توجه شرایط مسئله، تنش σ_S به صورت فشاری و تنش σ_B به صورت کششی خواهد بود. نکته قابل توجه این است که مقدار این تنش‌ها به طول مجموعه بستگی ندارند و با عکس مساحت مربوط به قطعه خود رابطه عکس دارند (σ_S/σ_B=A_B/A_S).

ب) تعیین افزایش طول مجموعه

با جایگذاری یکی از معادلات P_S یا P_B در معادله δ، تغییر طول کل مجموعه به دست می‌آید:

با استفاده از فرمول‌های به دست آمده می‌توانیم نیروها، تنش‌ها و جابجایی‌های مجموعه را به راحتی محاسبه کنیم.

نکته 1

برای اطمینان از صحت فرمول‌های به دست آمده می‌توانیم حالت‌های خاص مسئله را در نظر بگیریم. به عنوان مثال، فرض کنید که پیچ موجود در مجموعه مورد بررسی صلب باشد. در این صورت، تغییر دما هیچ تأثیری بر روی طول پیچ نخواهد داشت. برای نمایش این شرایط می‌توان α_B را برابر با صفر یا E_B را برابر با بی‌نهایت در نظر گرفت. در این شرایط، مجموعه‌ای به وجود می‌آید که پوشش آن بین تکیه‌گاه‌های صلب قرار گرفته است. با جایگذاری این مقادیر در فرمول‌های به دست آمده، به روابط زیر می‌رسیم:

این روابط با روابط به دست آمده در مثال قبل (میله قرار گرفته در میان تکیه‌گاه‌های صلب) مطابقت دارد.

نکته 2

فرض کنید که جنس مواد تشکیل‌دهنده پوشش و پیچ یکسان باشد. در این شرایط، با تغییر دمای مجموعه طول هر دو قطعه به صورت آزادانه و با مقداری برابر تغییر می‌کند. به این ترتیب، هیچ نیرو یا تنشی درون قطعات ایجاد نمی‌شود. با جایگذاری α_S=α_B=α در فرمول‌های به دست آمده، به روابط زیر می‌رسیم:

همان طور که مشاهده می‌شود، روابط بالا با توضیحات ارائه شده مطابقت دارند (عدم وجود تنش).

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های مهندسی عمران
• مجموعه آموزش‌های دروس مهندسی مکانیک
• آموزش مقاومت مصالح
• مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خصوصیات رفتاری مواد