جستجوی درون یابی (Interpolation Search) – به زبان ساده

در این مطلب، روش انجام «جستجوی درون یابی» (Interpolation Search) بیان و پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل  ++C، «جاوا» (Java)، «پایتون» (Python)، «سی‌شارپ» (#C) و «پی‌اچ‌پی» (PHP) انجام شده است. یک آرایه مرتب شده []arr از مقادیر دارای توزیع یکنواخت داده شده است. هدف نوشتن برنامه‌ای است که عنصر مشخص x را در آرایه جستجو کند.

مقدمه‌ای بر جستجوی درون‌یابی

«جستجوی خطی» (Linear Search) عناصر را در زمان O(n)‎، «جستجوی پرشی» (Jump Search) در زمان O(√ n)‎ و «جستجوی دودویی» (Binary Search) در زمان O(Log n)‎ جستجو می‌کند. جستجوی درون یابی نسخه بهبود یافته جستجوی دودویی برای نمونه‌ها است که در آن‌ها مقادیر در آرایه مرتب شده به طور یکنواخت توزیع شده‌اند.

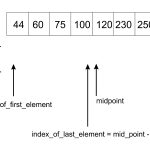
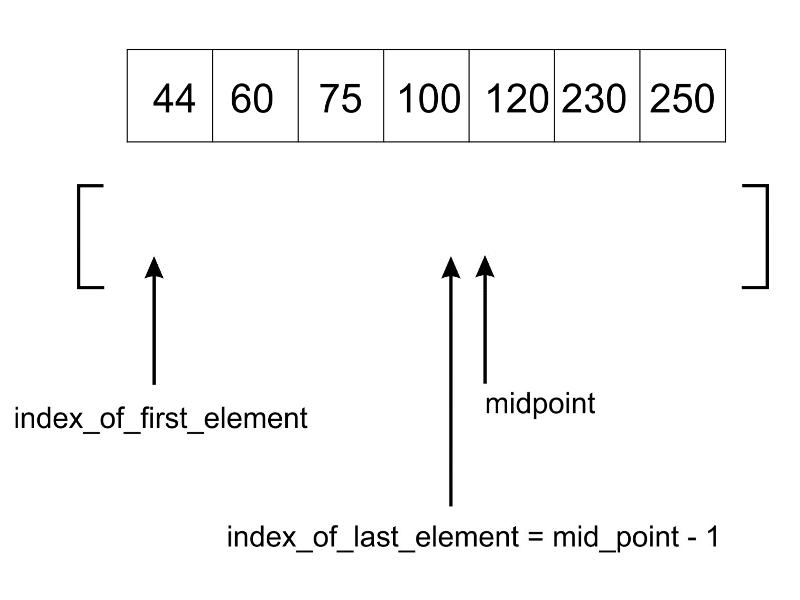
جستجوی دودویی همیشه به عنصر میانی می‌رود تا بررسی کند. در حالی که، جستجوی درون یابی مطابق با مقدار کلید به موقعیت‌های مختلف جستجو می‌رود و آن‌ها را جستجو می‌کند. برای مثال، اگر کلید به آخرین مقدار نزدیک‌تر باشد، جستجوی درون‌یابی احتمال دارد تا جستجو را از سمت انتهایی انجام دهد. برای پیدا کردن موقعیت جهت انجام جستجو، از رابطه زیر استفاده می‌شود.

// The idea of formula is to return higher value of pos
// when element to be searched is closer to arr[hi]. And
// smaller value when closer to arr[lo]
pos = lo + [ (x-arr[lo])*(hi-lo) / (arr[hi]-arr[Lo]) ]

arr[] ==> Array where elements need to be searched
x     ==> Element to be searched
lo    ==> Starting index in arr[]
hi    ==> Ending index in arr[]

الگوریتم جستجوی درون یابی

در ادامه، کلیت الگوریتم جستجوی درون یابی توضیح داده شده است.

فیلم آموزش طراحی الگوریتم – جامع و با مفاهیم کلیدی + گواهینامه در فرادرس

کلیک کنید

• گام ۱: در حلقه، مقدار «pos» را با استفاده از فرمول موقعیت کاوشگر محاسبه می‌کند.
• گام ۲: اگر مقدار موجود در آن اندیس با مقدار x تطبیق پیدا کرد، اندیس عنصر را بازگردان و خارج بشو.
• گام ۳: اگر عنصر کمتر از arr[pos]‎ است، موقعیت کاوشگر را از زیر آرایه سمت چپ پیدا کن. در غیر این صورت، در زیر آرایه سمت راست جستجو کن.
• گام ۴: تا هنگامی که یک عنصر مطابق پیدا شود یا زیر آرایه به صفر کاهش پیدا کند، کار را تکرار کن.

در ادامه، روش پیاده‌سازی الگوریتم بیان شده ارائه شده است.

جستجوی درون یابی در ++C

جستجوی درون یابی در C

جستجوی درون یابی در جاوا

جستجوی درون یابی در پایتون

فیلم آموزش الگوریتم های مرتب سازی در زبان برنامه نویسی پایتون با مثال (رایگان) در فرادرس

کلیک کنید

جستجوی درون یابی در #C

فیلم آموزش برنامه نویسی سورس کدهای الگوریتمی در سی شارپ C#‎ در فرادرس

کلیک کنید

جستجوی درون یابی در PHP

خروجی قطعه کد بالا به صورت زیر است.

Element found at index 4

اگر عناصر به طور یکنواخت توزیع شده باشند، پیچیدگی زمانی از درجه O (log (log n))‎ خواهد بود. در بدترین حالت می‌توان تا درجه O(n)‎ را به خود بگیرد. پیچیدگی فضای کمکی نیز از درجه O(1)‎ است.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده
• الگوریتم جست و جوی دودویی در جاوا اسکریپت — به زبان ساده

^^