قضیه مقدار میانی (Intermediate Value Theorem) — به زبان ساده

یکی از قضیه‌های مهم در ریاضیات و هندسه تحلیلی، قضیه مقدار میانی است. در این نوشتار سعی داریم که به بررسی این قضیه و کاربردهای آن بپردازیم.

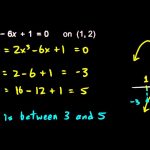
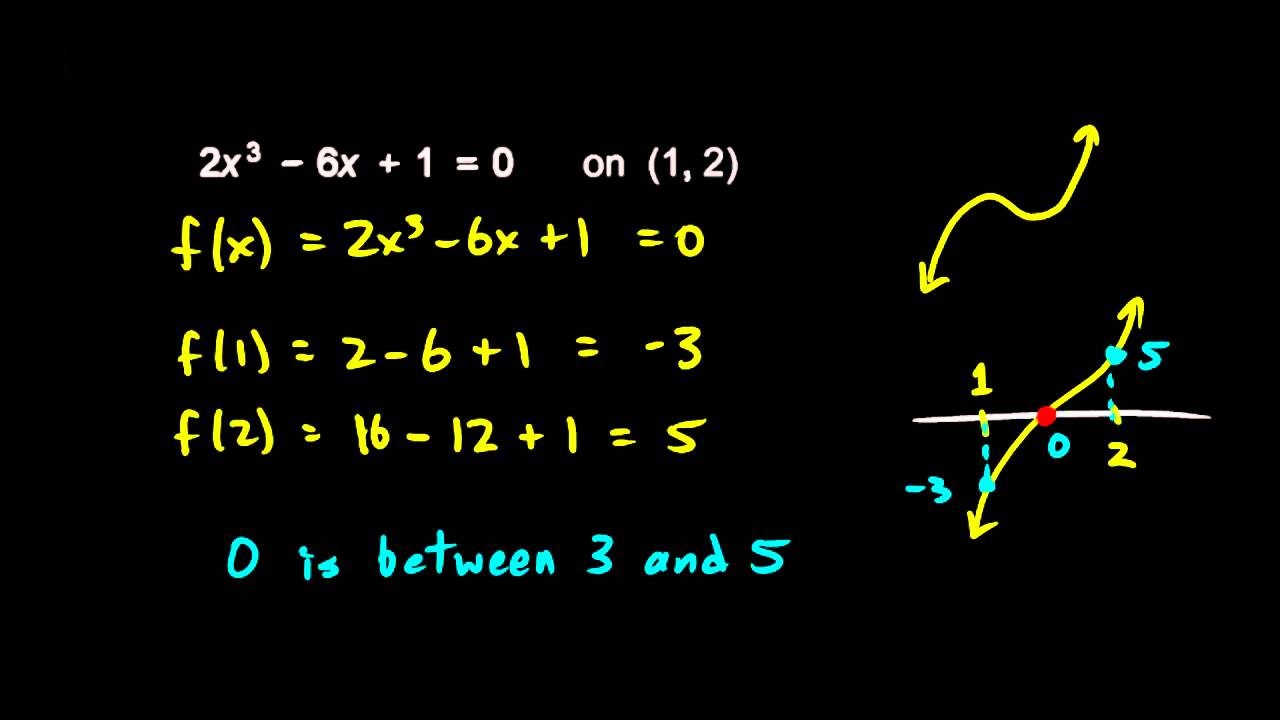
قضیه مقدار میانی

ایده اصلی در «قضیه مقدار میانی» (Intermediate Value Theorem) در نکته زیر نهفته است.

فیلم آموزش مبانی توپولوژی عمومی – جامع و کاربردی در فرادرس

کلیک کنید

اگر روی یک منحنی پیوسته، که از دو نقطه A و B می‌گذرد، خطی رسم کنیم که یک نقطه در بالا و یک نقطه در پایین خط ترسیمی قرار گیرد، حتما خط مورد نظر، منحنی را در حداقل یک نقطه قطع می‌کند. اگر این خط را همان محور افقی در نظر بگیریم، قضیه مقدار میانی کمک می‌کند که وجود ریشه را در یک معادله بررسی کنیم.

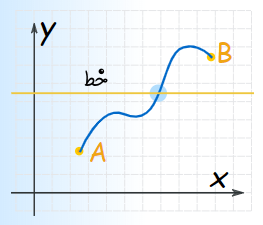
در عبارت بالا از اصطلاح، منحنی پیوسته استفاده شد که برای بیان قضیه مقدار میانی باید از مفهوم آن مطلع باشیم.

پیوستگی تابع یا منحنی

اگر در نمودار مربوط به منحنی، هیچ نقطه انقطاعی وجود نداشته باشد و یا هنگام ترسیم آن هرگز قلم را از کاغذ جدا نکنیم، منحنی یا تابع را پیوسته گویند. البته در ریاضیات و بحث توابع ریاضی، مفهوم پیوستگی به صورت کامل و خاص به کمک تعریف حد بیان می‌شود که در اینجا از بیان تعریف اصلی پیوستگی صرف نظر می‌کنیم تا از سادگی موضوع کاسته نشود.

فرم رسمی قضیه مقدار میانی

با توجه به مفهوم پیوستگی و مطالبی که در بالا گفته شد، قضیه مقدار میانی را معرفی کرده و برای درک آن از مثال‌های مختلفی کمک می‌گیریم.

در اینجا تابع $$f(x)$$ دارای شرایط زیر است:

• $$f(x)$$ روی بازه $$[a,b]$$ پیوسته است.
• W نقطه‌ای بین دو مقدار $$f(a)$$ و $$f(b)$$ است. $$\min(f(a),f(b))\leq W\leq \max(f(a),f(b))$$.

صورت قضیه: با توجه به شرایط بالا حداقل یک مقدار مثل c در بازه $$(a,b)$$ وجود دارد که $$f(c)=W$$.

دو نکته در این قضیه وجود دارد: 1- فاصله‌ای که c و $$W=f(x)$$ درون آن قرار دارد.

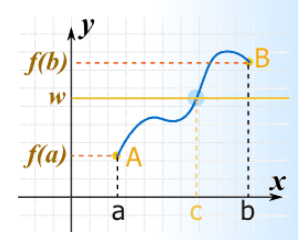
2- تضمین وجود حداقل یک مقدار برای c

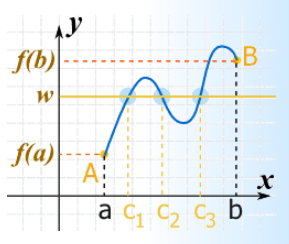
همانطور که در تصویر دیده می‌شود ممکن است نقاطی مثل $$C_1,C_2,C_3$$ وجود داشته باشند که در شرایط قضیه مقدار میانی صادق باشند.

کاربرد قضیه مقدار میانی

اگر درستی شرایط قضیه مقدار میانی برای یک منحنی ثابت شود، می‌توان نقطه‌ای روی خط پیدا کرد که منحنی را قطع کرده است. برای تاکید بیشتر این شرایط را تکرار می‌کنیم:

• منحنی پیوسته است.
• نقطه‌ای بالای خط در منحنی و نقطه‌ای پایین خط در منحنی وجود دارد.

مثال ۱

آیا برای معادله $$x^5-2x^3-2=0$$ ریشه‌ای در فاصله ۰ تا ۲ وجود دارد؟

می‌دانیم منظور از ریشه یک معادله، تقاطع منحنی آن با خط y=0 است. مشخص است که این خط همان محور افقی یا محور xها است.

برای حل این مسئله، ابتدا باید شرایط قضیه را بررسی کنیم.

منحنی $$x^5-2x^3-2=0$$ روی مجموعه اعداد حقیقی پیوسته است. زیرا می‌دانیم که همه چند جمله‌ای‌ها روی اعداد حقیقی پیوسته هستند.

برای بررسی شرط دوم مقدار تابع را در دو نقطه داده شده بررسی می‌کنیم.

$$f(x)=x^5-2x^3-2$$

$$f(0)=(0)^5-2(0)^3-2=-2$$

$$f(2)=(2)^5-2(2)^3-2=14$$

بنابراین خواهیم داشت:

$$f(0)=-2 \leq f(c)=0\leq f(2)=14$$

پس شرایط قضیه مقدار میانی وجود دارد و می‌توان c را در فاصله $$[0,2]$$ یافت که $$f(c)=0$$ باشد. واضح است که در اینجا به علت اینکه می‌خواهیم ریشه را پیدا کنیم W=۰ خواهد بود. پس حداقل یک ریشه برای این معادله در بازه $$[0,2]$$ وجود دارد.

به این ترتیب قضیه مقدار میانی را می‌توان به یان صورت تفسیر کرد که اگر دو نقطه a, b از فاصله $$(a,b)$$ وجود داشته باشند که $$f(a)f(b)<0$$ باشد، آنگاه حتما یک ریشه در فاصله $$(a,b)$$ برای f(x)=0‌ وجود دارد.

کاربردها در زندگی روزمره

در ادامه با چند مثال ساده به برخی از کاربردهای قضیه مقدار میانی در زندگی روزمره می‌پردازیم.

فیلم آموزش پیوستگی در مبانی آنالیز ریاضی (رایگان) در فرادرس

کلیک کنید

مثال ۲

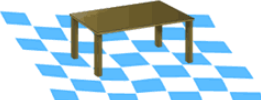
فرض کنید در آشپزخانه، میزی دارید که به علت ناهمواری سطح زمین، دچار لقی شده است. برای حل لقی میز، کافی است که آن را بچرخانید تا متعادل شود. حتما برایتان این سوال پیش می‌آید که این کار چه ربطی به قضیه مقدار میانی دارد. بهتر است شرایط مسئله را بررسی کنیم.

میز ما دارای چهار پایه است که سه تا از آن‌ها روی زمین قرار دارند ولی چهارمی به علت ناهمواری زمین، روی هوا باقی مانده است. از طرفی می‌توان ناهمواری سطح زمین را به صورت تابعی پیوسته در نظر گرفت (ناهمواری به علت وجود پله یا لبه‌های تیز بوجود نیامده است).

با چرخش میز، پایه چهارم گاهی در هوا قرار گرفته و گاهی هم با قرار گرفتن روی زمین باعث بالاتر رفتن پایه‌های دیگر از زمین خواهد شد. به این ترتیب به نظر می‌رسد نقطه‌هایی روی منحنی سطح زمین آشپزخانه قرار دارند که کوتاه‌تر (کمتر) و یا بلندتر (بیشتر) از نقطه تراز (خط تراز) هستند.

در نتیجه شرایط قضیه مقدار میانی وجود دارد و با چرخش میز می‌توانید به نقطه‌ای از سطح زمین (منحنی) برسید که در آن، پایه میز (خط مورد نظر) منحنی (سطح زمین آشپزخانه) را در محل درست (فاصله بین پایه چهارم و زمین برابر با صفر باشد) قطع می‌کند.

مثال ۳

فرض کنید در مسیری در حال حرکت هستید. در طی مسیر، به نقاطی خواهید رسید که از نقطه شروع شما بلندتر یا کوتاه‌تر هستند. طبق قضیه مقدار میانی، اگر مسیر حرکت شما پیوسته باشد، حتما در طی مسیر به نقاطی برخورد خواهید کرد که با نقطه شروع اولیه شما هم ارتفاع خواهند بود.

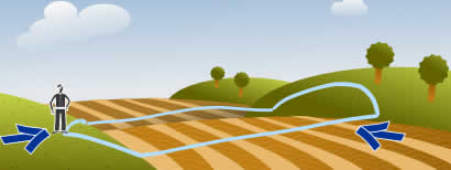
نکته: البته باید در نظر گرفت که نقطه شروع شما یکی از کوتاه‌ترین یا بلندترین نقاط مسیر نیست.

این وضعیت را برای دما، فشار یا پدیده‌های دیگر نیز می‌توان در نظر گرفت. برای مثال اگر تغییرات دما پیوسته باشد، حداقل یک روز در سال می‌توان پیدا کرد که دمایی مشابه امروز داشته باشد. البته با فرض اینکه دمای امروز کمترین و یا بیشترین دما در طول سال نیست. در چنین حالتی باز هم قضیه مقدار میانی کاربرد دارد.

مثال ۴

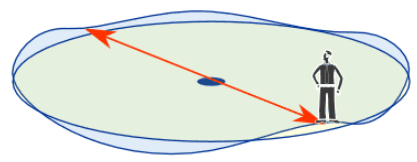
فرض کنید روی مسیر دایره‌ای شکلی در حال حرکت هستید که دارای پستی و بلندی است. نقاطی در روی این مسیر وجود دارد که دارای میزان ارتفاع یکسانی هستند. در این جا هم شرایط قضیه مقدار میانی برای این مسیر وجود دارد. منحنی حرکت پیوسته است و همه مسیر بین دو نقطه با کمترین ارتفاع و بیشترین ارتفاع طی می‌شود. البته باز هم باید دو نقطه با بیشترین و کمترین ارتفاع را استثناء کرد.

به نظر می‌رسد که ریاضیات با ایده‌هایی ساده از زندگی روزمره آغاز شده است و بیشتر مفاهیم اصلی و پایه‌ای آن به راحتی قابل درک باشند. مثال‌هایی متعددی در این زمینه‌های می‌توان پیدا کرد که استفاده از ریاضیات کارگشایی بسیاری از مسائل خواهد بود. پس بهتر است با این علم که یکی از ناب‌ترین دستاوردهای عملی بشر است بیشتر آشنا شویم تا از شیرینی آن لذت ببریم و همچنین حلاوت آن را به دیگران انتقال دهیم.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های ریاضی و فیزیک
• آموزش ریاضی عمومی ۲
• آموزش ریاضیات عمومی ۱
• انتگرال — به زبان ساده
• مشتق — به زبان ساده
• اعداد حقیقی — به زبان ساده

^^