روش تغییر متغیر برای حل انتگرال — به زبان ساده

پیش‌تر در وبلاگ فرادرس، در مورد مفاهیم انتگرال و هم‌چنین روش جزء به جزء‌ در محاسبه انتگرال صحبت کردیم. در این قسمت قصد داریم تا تکنیکی جدید را به‌منظور بدست آوردن انتگرال معرفی کنیم. در مطالب گذشته عنوان شد که در محاسبه انتگرال از مفهوم عکس بودن آن نسبت به مشتق استفاده می‌شود. در بعضی از موارد می‌توان به راحتی از این مفهوم استفاده کرد. برای نمونه از آنجایی که مشتق x² برابر با 2x است، بنابراین رابطه $$\int 2xdx=x^2+C$$ برقرار است. همین داستان در مورد توابع ساده دیگری هم‌چون sin x ،e^x و $$1 \over x$$ نیز صادق است. اما در بعضی از موارد نمی‌توان حاصل انتگرال را با استفاده از این مفهوم و به سادگی حدس زد. برای نمونه حاصل cos(3x+5)dx ∫ برابر با sin(3x+5)+C نمی‌شود. در چنین مواردی می‌توان از تکنیک‌های انتگرال‌گیری مختلفی استفاده کرد. یکی از این تکنیک‌های معروف که کاربرد بسیاری نیز دارد، روش تغییر متغیرها است. توجه کنید که روش کلی تغییر متغیر در ریاضیات در مطلب «تغییر متغیر — به زبان ساده» به صورت دقیق مورد مطالعه قرار گرفته است. در مواردی نیز می‌توان انتگرال را در دیگر دستگاه‌های مختصات محاسبه کرد. در آینده نحوه محاسبه انتگرال در دستگاه مختصات استوانه‌ای را توضیح خواهیم داد.

روش تغییر متغیر‌ها در محاسبه انتگرال نامعین توابع

تصور کنید که می‌خواهیم حاصل انتگرال تابع 2xcos x² را بیابیم. اگر به این تابع دقت کنید متوجه می‌شوید که مشتق x² در بخش دیگری از تابع ظاهر شده است. بنابراین رابطه 2xcos x² از یک تابع و مشتقش بوجود آمده است.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

در حقیقت اگر x² را برابر با u و تابع cos را معادل با w در نظر بگیریم،‌ عبارت زیر انتگرال را می‌توان به شکل زیر، بر حسب u بازنویسی کرد.

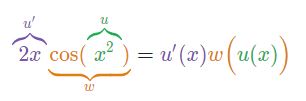
برای یافتن انتگرال توابعی هم‌چون این مثال، در ابتدا بخشی از عبارت را به عنوان u در نظر بگیرید، سپس تابع زیر انتگرال را بر حسب u بازنویسی کنید. برای نمونه در تابع 2xcos x² می‌توان x² را برابر با u در نظر گرفت، در نتیجه 2xdx معادل با du است. در ابتدا رابطه بین دیفرانسیل dx و du را مطابق با عبارت زیر می‌نویسیم.

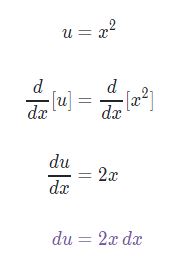
با توجه به عبارات بالا می‌توان تابع را به شکل زیر،‌ بر حسب u نوشت:

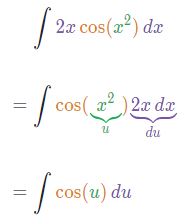
همانگونه که می‌دانید حاصل انتگرال تابع cos u برابر با sin u است. با بدست آمدن انتگرال بر حسب u و جایگذاری x به جای آن، پاسخ نهایی بر حسب x یافت می‌شود. توضیحات بیان شده به شکل زیر قابل نوشته شدن هستند:

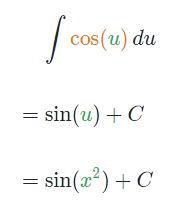
برای چک کردن صحت پاسخ بدست آمده، می‌توان از تابع sin x² مشتق گرفت و دید آیا 2x cos x² ظاهر می‌شود یا خیر. مشاهده می‌کنید که حاصل مشتق sin x² برابر با 2xcos x² است.

بنابراین شکل کلی تابع زیر انتگرال، در این روش، به صورت زیر است.

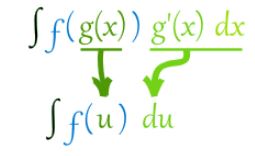
برای نمونه در مثالی که زده شد، رابطه بالا به شکل زیر است.

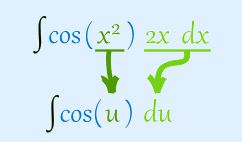
به‌منظور تسلط بیشتر به این روش می‌توانید از مثال‌های بیان شده در این آموزش استفاده کنید. در ادامه نیز مثال‌هایی ذکر شده که توجه شما را به آن‌ها جلب می‌کنیم.

مثال ۱: $$\int \frac {x} {x^2+1}dx$$

برای حل انتگرال به این روش در ابتدا به تابع زیر انتگرال نگاه کنید و بررسی کنید که آیا می‌توان یک عبارت به همراه مشتقش را در آن یافت.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

توجه داشته باشید که در بعضی مواقع با کمی تغییر می‌توان تابع را به شکلی بیان کرد که با استفاده از روش تغییر متغیر‌ قابل حل باشد. برای نمونه می‌توان این انتگرال را در عدد ثابت ۲ ضرب و تقسیم کرد و آن را به شکل زیر نوشت:

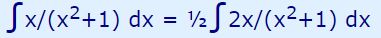
همان‌گونه که از رابطه بالا نیز می‌توان دید، با فرض x²+1 برابر با u، مشتق آن نیز به صورت 2x در صورت ظاهر شده است. بنابراین انتگرال مفروض را می‌توان به صورت زیر بیان کرد:

همان‌طور که از قبل می‌دانید، انتگرال تابع $$\frac {1}{u}$$ برابر با ln u است. در نتیجه داریم:

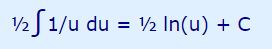
با جایگذاری u=x²+1، حاصل انتگرال بر حسب x و به صورت زیر بدست می‌آید.

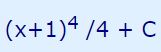
در برخی از مسائل که تابع زیر انتگرال شامل عبارات با توان بالا است،‌ می‌توان از روش تغییر متغیر استفاده کرد. در مثال زیر روش انتگرال‌گیری از تابعی دوجمله‌ای که به توان بالایی رسیده، بیان شده است.

مثال ۲: $$\int {(5x+2)}^7dx$$

در این مثال نیز انتگرال را در عدد ثابت ۵ ضرب و تقسیم می‌کنیم. با انجام این کار خواهیم داشت:

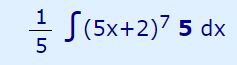
با نگاهی اولیه به تابع متوجه می‌شوید که مشتق 5x+2 که همان ۵ باشد، در تابع وجود دارد. پس می‌توان از روش تغییر متغیرها در این مسئله استفاده کرد. از این رو می‌توان تابع u را به شکل زیر در نظر گرفت:

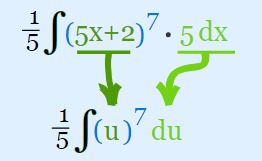
هم‌چنین از اصول انتگرال می‌دانید که:

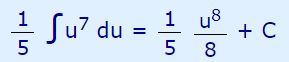
بنابراین حاصل انتگرال بر حسب u یافت شد. حال کافی‌ است که در عبارت بدست آمده در بالا، به جای u تابع 5x+2 را قرار دهیم. با انجام این کار شکل نهایی پاسخ انتگرال برابر است با:

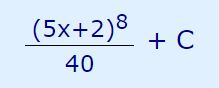
در ادامه انتگرال تابع شناخته شده tan x را محاسبه می‌کنیم.

مثال ۳: $$\int tan (x)dx$$

همان‌گونه که از ریاضیات پایه می‌دانیم،‌ این تابع برابر با sin x/cos x است. از طرفی این توابع در مشتق‌گیری به یکدیگر تبدیل می‌شوند. در حقیقت با در نظر گرفتن cos x به عنوان u، مشتق آن در صورت ظاهر شده است. در در نتیجه می‌توان نوشت:

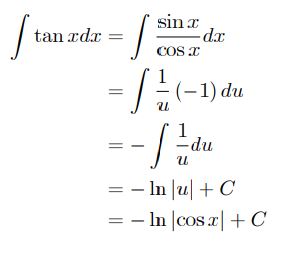
مثال ۴: $$\int \frac {ln (x)}{x}dx$$

در نگاه اول می‌توان فهمید که مشتق تابع ln x  به صورت $$\frac {1}{x}$$ در صورت مسئله ظاهر شده. در نتیجه u را می‌توان به شکل زیر فرض کرد.

u= ln (x)

در نتیجه دیفرانسیل u برابر است با:

du= (1/x)dx

بنابراین پاسخ این انتگرال به ترتیب زیر بدست می‌آید.

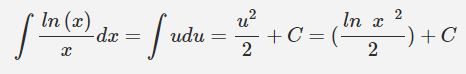
روش تغییر متغیر تکنیکی بسیار مفید جهت محاسبه انتگرال محسوب می‌شود. از این رو می‌توانید جهت حل مثال‌های بیشتر و تسلط روی موضوع به این لینک مراجعه کنید.