نظریه اطلاع و بی نظمی — مفاهیم اولیه

زمانی که ایده یا نظری در ذهن دارید، باید برای انتقال یا حتی حفظ آن، اطلاعات نهفته در نظر یا ایده خود را به شکلی پیاده‌سازی کنید تا برای دیگران قابل دسترس و فهم باشد. شاید بخشی از این موضوع، مربوط به ساختار دستور زبان و زبان شناسی، تمثیل شناسی و ... می‌شود. این موضوعات بیشتر در بحث مربوط به اصول روابط عمومی و ساختارهای زبان‌شناسی و علوم رفتار نهفته است. ولی در اینجا قصد داریم از جنبه «نظریه اطلاع و بی نظمی» (Information Theory and Entropy) به این مفاهیم توجه کرده و از نگاه «میزان اطلاعات» (Quantification)، «ذخیره‌سازی» (Storage) و «انتقال اطلاعات» (Communication) برگرفته از پدیده‌های تصادفی به آن بنگریم که خوشبختانه این مباحث مربوط به حوزه «نظریه اطلاع مدرن» (Modern Information Theory) هستند. این نظریه، توسط ریاضی‌دان و مهندس برق «کلود شانون» (Claude Shannon) در سال ۱۹۴۸ تحت مقاله‌ای با عنوان «نظریه ریاضی مخابرات» (A Mathematical Theory of Communication) معرفی شد. او در آن مقاله تاکید کرد که باید مفهوم اطلاعات را از سینگال‌های حامل آن‌ها جدا کرد و بطور مجزا مورد بررسی قرار داد.

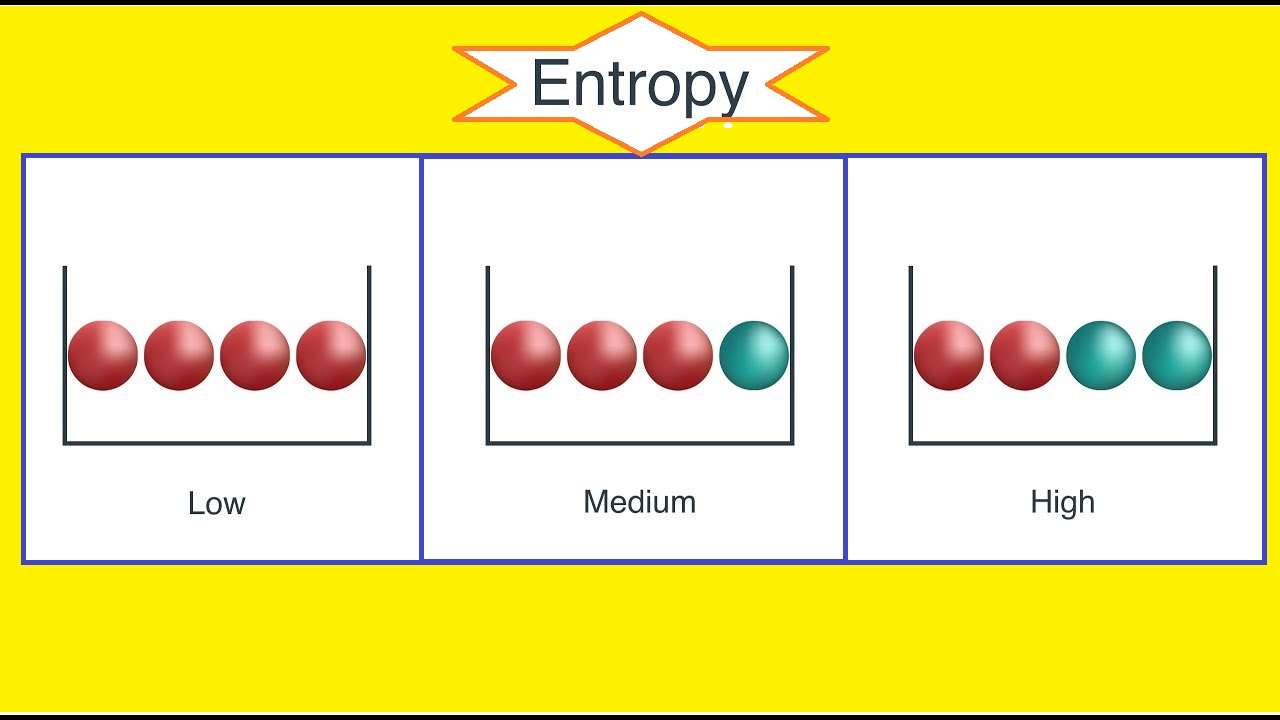
در این نوشتار با استفاده از اصول احتمال و مفاهیم اولیه پدیده‌های تصادفی و البته متغیرهای تصادفی، به بررسی نظریه اطلاع پرداخته و با اصطلاحات و مفاهیم اولیه آن آشنا خواهیم شد. به این منظور بهتر است ابتدا از اصول احتمال آگاهی نسبی داشته باشید. بنابراین مطالعه نوشتارهای دیگر فرادرس با عنوان آزمایش تصادفی، پیشامد و تابع احتمال و متغیر تصادفی، تابع احتمال و تابع توزیع احتمال پیشنهاد می‌شود.

همچنین خواندن مطالب امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها و یادگیری ماشین به زبان قضیه بیز، بی نظمی شانون و فلسفه نیز خالی از لطف نیست. از آنجایی که مفهوم بی‌نظمی (Entropy) در ترمودینامیک بسیار به نظریه اطلاع با مفهوم احتمالی آن نزدیک است، مطالعه آنتروپی — از صفر تا صد نیز توصیه می‌شود.

نظریه اطلاع و بی نظمی

براساس نظریه انقلابی و اساسی شانون، برای اولین بار مفهوم اندازه اطلاعات و مدل‌های مخابراتی به عنوان یک فرآیند آماری مطرح شد. او نظریه خود را براساس یک هدف اساسی پایه‌ریزی کرد. وی اساس و مسئله اصلی در حوزه انتقال داده‌ها را به صورت زیر مطرح کرد.

فیلم آموزش ترکیب اطلاعات Information Fusion در فرادرس

کلیک کنید

«مسئله اصلی در مخابرات، تولید یک پیام و سپس باز تولید آن در مکان دیگر است به شکلی که اطلاعات مبدا و مقصد دقیقا یا با خطای قابل قبولی، یکسان باشند.»

با توجه به رویکرد جدید شانون به اطلاعات و نقش آن در مخابرات، مفاهیم و ایده‌های دیگری نیز ظهور کرد. در فهرست زیر بعضی از این مفاهیم و اصطلاحات معرفی شده‌اند.

• نظریه اطلاع و «افزونگی» (Redundancy) منبع.
• اطلاع متقابل (Mutual Information) و ظرفیت یک کانال دارای نویز.
• قانون شانون-هارتلی (Shannon-Harltey Law) برای ظرفیت کانال با نویز گاووسی.
• مفهوم بیت (bit) به عنوان پایه و کوچکترین واحد اطلاعاتی.

با استفاده از نظریه اطلاع و اصطلاحات مطرح شده در بالا، علوم دیگری نظیر، «رمز‌نگاری» (Cryptography)، «نظریه شبکه فعال» (Active Networking)، «علم سایبرنتیک» (Cybernetic) و ... نیز بوجود آمده که با توجه به احاطه دانش پردازش اطلاعات، از علوم مطرح در قرن حاضر محسوب می‌شوند بطوری که نظریه‌های مربوط به آن لبه‌های دانش امروزی را تشکیل می‌دهند.

در این نوشتار، بیشتر بر شیوه و روش‌های اندازه‌گیری اطلاعات بخصوص اندازه بی نظمی متمرکز خواهیم بود. به این منظور برای نمایش میزان بی‌نظمی متغیر تصادفی $$X$$ از نماد $$H(X)$$ استفاده خواهیم کرد. نماد $$H$$ به علت تعریف آنتروپی (بی‌نظمی) در مکانیک آماری گازها که توسط دانشمند مکانیک «بولتزمن» (Botlzmann) معرفی شد، در اینجا نیز به کار گرفته می‌شود. در این میان نقش «رالف هاترلی» (Ralph Hartley) که مبانی نظریه اطلاع را پایه‌ریزی کرد، نیز نباید نادیده گرفته شود.

اندازه‌ اطلاع و بی نظمی

یکی از قسمت‌های نظریه اطلاع مرتبط با شیوه «اندازه اطلاع» (Quantities of Information) و «بی نظمی« (Entropy) است. به این ترتیب حداقل می‌توان میزان اطلاعات ارسال شده و دریافت شده از منبع و مقصد را مقایسه کرد تا قسمتی از مسئله اصلی در مخابرات که در بالا به آن اشاره شد، را حل کرد. بنابراین احتیاج به روش و واحدی برای اندازه‌گیری اطلاعات احتیاج است.

فیلم آموزش مفاهیم پایه نظریه ترکیب اطلاعات (رایگان) در فرادرس

کلیک کنید

از آنجایی که نظریه اطلاع، برمبنای تئوری احتمال و آمار بنا شده است، نحوه اندازه‌گیری اطلاعات را به کمک متغیر تصادفی تعیین می‌کنند. به این ترتیب دو مفهوم جدید به نام‌های «بی‌نظمی» (Entropy) و «اطلاع متقابل» (Mutual Information - MI) معرفی می‌شوند. بی‌نظمی به شکلی براساس میزان تابع چگالی احتمال یک متغیر تصادفی محاسبه می‌شود در حالیکه اطلاع متقابل و اطلاع توام برحسب تابع چگالی توام دو متغیر تصادفی بدست می‌آید.

اندازه بی‌نظمی برای یک منبع اطلاعاتی (پیام)

براساس نظریه آمار و احتمال، تابع چگالی احتمال $$f_X(x)=p(x)$$ متغیر تصادفی $$X$$، بیانگر جرم احتمال در نقطه $$x$$‌ است. بنابراین اگر برای هر بیت (واحد سنجش اطلاعات) تابع چگالی احتمال را با $$p_i$$‌ نشان دهیم، می‌توانیم اطلاعاتی که در آن موجود است را براساس رابطه $$I(x)=-\log_2(p_i)$$ محاسبه کنیم. مقدار $$I(x)$$ را «خود-اطلاع» (Self-information) می‌نامیم. می‌توان رابطه محاسباتی $$I(X)$$‌ را برای راحتی به شکل زیر نیز نوشت:

$$\large I(X)=\log_2\dfrac{1}{p_i}$$

به این ترتیب اگر پیشامدی دارای احتمال رخداد $$0.75$$ یا $$0.25$$ باشد، میزان اطلاع یا بی‌نظمی آن‌ها به صورت زیر محاسبه می‌شود.

$$\large I(X)= \log_2 \dfrac{1}{0.75}=\log_2(1.333)=0.41$$

$$\large I(X)= \log_2 \dfrac{1}{0.25}=\log_2(4)=2$$

نکته: از آنجایی که داده‌ها به صورت باینری هستند از لگاریتم برمبنای ۲ استفاده کرده‌ایم. البته به حالت کلی‌تر می‌توان برای اندازه‌گیری میزان اطلاعات از هر نوع لگاریتمی استفاده کرد. انتخاب نوع لگاریتم فقط در مقیاس اندازه‌گیری اطلاعات تغییر بوجود می‌آورد.

مشخص است که برای پیشامد نادر مقدار $$p_i$$ بسیار کوچک خواهد بود و در عوض مقدار خود-اطلاع آن بسیار بزرگ است زیرا  وقوع این پیشامد شامل اطلاعات زیادی است. برعکس اگر برای یک پیشامد قطعی (که از وقوع آن مطمئن هستیم)، مقدار خود-اطلاع محاسبه شود، مقداری نزدیک به صفر خواهد بود که نشانگر میزان کوچک اطلاعات در این پیشامد است. به نظر می‌رسد که این مفهوم با درک و منطق بشری نیز یکسو است.

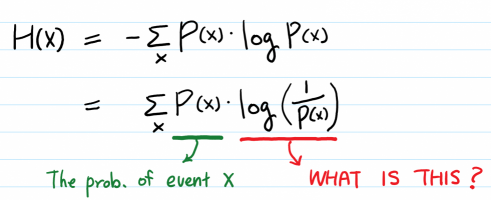
به این ترتیب اگر اجزای یک پیام‌ یک متغیر تصادفی ($$X$$) باشند، امید ریاضی $$p_i$$ به عنوان میزان بی‌نظمی شانون نامیده شده و به شکل زیر محاسبه می‌شود.

$$\large H(X)=-\sum_i p_i \log_2(p_i)$$

همانطور که دیده می‌شود، به نظر می‌رسد ارتباط نزدیکی بین شیوه محاسبه میزان بی‌نظمی و «اطلاع فیشر» (Fisher Information) وجود دارد زیرا هر دو برحسب امید ریاضی تابع چگالی نوشته شده‌اند. البته گاهی مقدار $$H(X)$$ را به صورت زیر نیز بازنویسی می‌کنند.

$$\large H(X)=\sum_i p_i \log(\dfrac{1}{p_i})$$

مشخص است که در رابطه اخیر، ضریب منفی به صورت توان منفی درون تابع لگاریتم نوشته شده و باعث شده که کسر $$\frac{1}{p_i}$$ ظاهر شود. همانطور که مشخص است این شیوه محاسبه هم امید ریاضی $$\frac{1}{p_i}$$ خواهد بود. به بیان دیگر بی‌نظمی برای یک متغیر تصادفی بیانگر میزان اطلاعاتی است که در اختیار دارد. هر چه متغیر تصادفی بی‌‌نظمی بیشتری داشته باشد، حامل اطلاعات بیشتری نیز هست.

به این ترتیب اگر یک پیام مثل $$M$$ از $$N$$ جزء تشکیل شده باشد که هر یک از اجزای متغیر تصادفی گسسته و مستقل و هم‌توزیع (iid) (دارای تابع چگالی یکسان) باشند، میزان بی‌نظمی پیام به شکل زیر محاسبه می‌شود.

$$\large H(M)=N \cdot H(X)=-N\cdot E_X[I(x)]=-N\cdot \sum_{x\in S_X}p(x)\log p(x)=N\cdot \sum_{x\in S_X}p(x)\log \dfrac{1}{p(x)}$$

مشخص است که در اینجا تکیه‌گاه متغیر تصادفی $$X$$‌ با $$S_x$$‌ نشان داده شده و به صورت $$\{x_1,x_2,\ldots,x_n\}$$‌ نوشته می‌شود. همچنین اگر فرض کنیم $$p(i)=p(x_i)$$، مشخص است که $$p(i)$$ مقدار احتمال را برای نقطه $$x_i$$ یا نقطه $$i$$ام نشان می‌دهد.

به این ترتیب اگر پیامی به صورت HHHH‌ مخابره شود، میزان اطلاعی که به همراه دارد، بسیار کمک است زیرا احتمال رخداد H برابر با ۱ برآورد می‌شود که در حالت کلی یک پیشامد قطعی است. براساس رابطه قبل میزان بی‌نظمی برای چنین پیشامدی را محاسبه می‌کنیم.

$$\large N\cdot H(X)=4 \times \sum_i p_i \log_2(\dfrac{1}{p_i})=4 \times \sum_i \frac{1}{1} \log_2(\frac{1}{1})=\log_2\frac{1}{1}=0$$

ولی اگر پیشامد ABCD را در نظر بگیریم، میزان اطلاع در آن به بیشترین مقدار ممکن خواهد رسید زیرا احتمال هر یک از مقدارها برابر با $$\frac{1}{4}$$ برآورد شده و میزان بی نظمی به صورت زیر محاسبه می‌شود.

$$\large N \cdot H(X)=4 \times \sum_i p_i \log_2(\dfrac{1}{p_i})=4 \times \sum_i \frac{1}{4} \log_2(\frac{1}{4})=4 \times \log_2\frac{1}{4}=4 \times \log_2 4=8$$

نکته: اگر متغیرهای تصادفی تشکیل دهنده پیام، هم‌توزیع ولی مستقل نباشند، مقدار بی‌نظمی آن‌ها از $$N\cdot H(X)$$ کوچکتر خواهد بود، زیرا داریم:

$$\large p(x,y)\leq p(x)p(y)$$

مثال ۱

فرض کنید تابع چگالی برای متغیر تصادفی $$X$$ به شکل توزیع یکنواخت گسسته باشد، به این معنی که هر یک از مقادیر محتمل برای متغیر تصادفی $$X$$، با احتمال $$\dfrac{1}{n}$$ رخ دهد. در این صورت مقدار بی‌نظمی برای یک واحد پیام برابر با رابطه زیر است. این مقدار حداکثر میزان اطلاع برای واحد پیام (bit) محسوب می‌شود. به این ترتیب اگر اجزای پیام با توزیع تصادفی یکنواخت ارسال شوند اطلاعات بیشتری را به همراه دارند.

$$\large H(X)=E[I(x)]=-\sum \dfrac{1}{n}\cdot \log \dfrac{1}{n}=-\log{1}+\log{n}=\log n$$

مثال ۲

فرض کنید متغیر تصادفی $$X$$ دو وضعیتی (باینری) باشد. مشخص است که این متغیر تصادفی دارای توزیع برنولی با پارامتر احتمال موفقیت $$p$$ است. در این صورت تابع احتمال آن به شکل زیر خواهد بود.

$$\large p(x)=p^x(1-p)^{(1-x)},\;\;\;x=0,1$$

در این صورت اگر $$p(i)=p(x)$$ باشد، در نتیجه میزان بی‌نظمی برای چنین پیامی به شکل زیر مورد محاسبه قرار می‌گیرد.

$$\large H_{\mathrm {b} }(p)=-p\log _{2}p-(1-p)\log _{2}(1-p)$$

چنین رابطه‌ای را به نام «تابع بی‌نظمی باینری» (Binary Entropy Function) یا به افتخار کلود شانون دانشمند ابداع کننده مفهوم بی‌نظمی، «تابع بی‌نظمی شانون» می‌نامند. در ادامه نمودار این تابع برحسب میزان $$p(x)$$‌ ترسیم شده است. در این نمودار، محور افقی مقدارهای احتمال موفقیت و محور عمودی نیز میزان بی‌نظمی را نشان می‌دهد.

در ادامه کدی به زبان پایتون تهیه کرده‌ایم که قادر به انجام محاسبه بی‌نظمی برای رشته‌های متنی است که در تلگراف‌ها و به رمز درآوردن پیام به کار می رود. ابتدا بطوری تصادفی حروفی تولید می‌شوند و سپس با استفاده از روابط گفته شده در قسمت قبل، میزان بی‌نظمی یا انتروپی آن مورد محاسبات قرار می‌گیرد. در اینجا احتمالات رخداد هر یک از حروف توسط فراوانی نسبی بدست می‌آید. البته برای لگاریتم‌گیری نیز از مبنای ۲ استفاده شده است.

1import math 
2import random
3def H(sentence): 
4    """
5    (Shannon's Entropy) is implemented.
6    """
7    entropy = 0 
8    # There are 256 possible ASCII characters
9    for character_i in range(256): 
10        Px = sentence.count(chr(character_i))/len(sentence) 
11        if Px > 0: 
12            entropy += - Px * math.log(Px, 2) 
13    return entropy
14# The telegrapher creates the "encoded message" with length 10000.
15# When he uses only 32 chars 
16simple_message ="".join([chr(random.randint(0,32)) for i in range(10000)])
17# When he uses all 255 chars
18complex_message ="".join([chr(random.randint(0,255)) for i in range(10000)])

ابتدا یک عبارت تصادفی با طول ۱۰۰۰۰ حرف تشکیل می‌شود که از کدهای اسکی ۰ تا ۳۲ تشکیل می‌شود (حالت simple_message). در مرحله بعد نیز از همه کدهای اسکی برای رمز‌نگاری استفاده می‌شود در نتیجه در این حالت پیچیدگی نوشته رمزنگاری شده، بسیار بیشتر است (حالت complex_message)، بر همین مبنا میزان بی‌نظمی اطلاعات نیز افزایش خواهد یافت. خروجی برای اجرای این دستور به صورت زیر خواهد بود.

1In [20]: H(simple_message)
2Out[20]: 5.0426649536728  
3In [21]: H(complex_message)
4Out[21]: 7.980385887737537

اندازه بی‌نظمی برای دو منبع اطلاعاتی (پیام)

در قسمت قبلی برای یک پیام که از ترکیب چند جزء با متغیرهای تصادفی مستقل و هم‌توزیع ساخته می‌شود، بی‌نظمی را محاسبه کردیم. حال به مسئله محاسبه اندازه بی‌نظمی یا اندازه اطلاع براساس دو منبع اطلاعاتی برحسب «توزیع احتمال توام» (Joint Distribution) خواهیم پرداخت. در اینجا فرض می‌کنیم که دو متغیر تصادفی گسسته $$X$$ و $$Y$$ به همراه توزیع توام آن‌ها یعنی $$f_{X,Y}(x,y)$$ موجود است. به این ترتیب «بی‌نظمی توام» (Joint entropy) یا اندازه «اطلاع توام» (Joint Information) این دو متغیر تصادفی به شکل زیر تعریف و محاسبه می‌شود.

$$\large H(X,Y)=\mathbb {E} _{X,Y}[-\log p(x,y)]=-\sum _{x,y}p(x,y)\log p(x,y)$$

نکته: واضح است که اگر این دو متغیر تصادفی، مستقل از یکدیگر باشند، رابطه به شکل ساده‌تری که در ادامه قابل مشاهده است، در خواهد آمد. باز هم به نظر می‌رسد در این صورت نیز ارتباط جالبی بین اطلاع فیشر و بی‌نظمی برقرار است.

$$\large H(X,Y)=\mathbb {E} _{X,Y}[-\log p(x,y)]=-\sum _{x,y}p(x,y)\log p(x,y)=\\ \large -\sum_y\sum_xp(x)p(y)\left(\log p(x)+\log p(y)\right)=\\ \large H(X)\sum_yp(y)+H(Y)\sum_xp(x)=H(X)+H(Y)$$

اندازه بی‌نظمی شرطی

«بی‌نظمی شرطی» (Conditional Entropy) یا ابهام متغیر تصادفی (پیام) $$X$$ بر حسب یا درباره پیام $$Y$$ به صورت زیر تعریف و محاسبه می‌شود.

$$\large H(X|Y)=\mathbb {E} _{Y}[H(X|y)]$$

براساس این تعریف، مشخص است که این مقدار بیانگر میانگین بی‌نظمی شرطی $$X|Y$$ است. می‌دانیم که بین تابع چگالی شرطی و چگالی توام دو متغیر تصادفی $$X$$ و $$Y$$ رابطه زیر برقرار است.

$$\large f_{X|Y}(x,y)=\dfrac{f_{X,Y}(x,y)}{f_Y(y)}$$

در نتیجه می‌توان بی‌نظمی یا میزان اطلاع شرطی را برای متغیر تصادفی $$X$$ برحسب $$Y$$ به صورت زیر نشان داد.

$$\large H(X|Y)=-\sum _{y\in Y}p(y)\sum _{x\in X}p(x|y)\log p(x|y)=-\sum _{x,y}p(x,y)\log p(x|y)$$

توجه داشته باشید که طبق تعریف تابع چگالی شرطی و تابع چگالی حاشیه‌ای داریم:

$$\large p(x|y)=\dfrac{p(x,y)}{p(y)}, \;\;\; \sum_x p(x,y)=p(y)$$

بر اساس رابطه بالا می‌توان بین بی‌نظمی شرطی و بی‌نظمی توام تساوی زیر را برقرار کرد.

$$\large H(X|Y)=H(X,Y)-H(Y)$$

اندازه اطلاع متقابل

یکی دیگر از شیوه‌های اندازه‌گیری اطلاع برای دو متغیر تصادفی $$X$$ و $$Y$$ استفاده از اندازه اطلاع متقابل (Mutual Information - MI) است. درحقیقت می‌توان MI را میزان اطلاعاتی در نظر گرفت که یکی از متغیرها با توجه به مشاهده متغیر دیگر به همراه دارد. یکی از مسائلی که در مخابرات و ارسال و دریافت پیام‌ها اهمیت دارد، حداکثرسازی میزان اطلاعاتی است که بین سیگنا‌ل‌های ارسالی و دریافتی وجود دارد. به این ترتیب می‌توان حجم اطلاعات دریافتی یا ارسالی را کاهش داد.

فیلم آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS در فرادرس

کلیک کنید

میزان اطلاع متقابل برای متغیر تصادفی $$X$$ نسبت به $$Y$$ به شکل زیر تعریف و محاسبه می‌شود.

$$\large I(X;Y)=\mathbb {E} _{X,Y}[SI(x,y)]=\sum _{x,y}p(x,y)\log {\frac {p(x,y)}{p(x)\,p(y)}}$$

در اینجا $$SI$$ به صورت زیر تعریف شده و به آن میزان «اطلاع متقابل خاص» (Specific Mutual Information) گفته می‌شود. گاهی به $$SI$$ «اطلاع متقابل نقطه‌ای» (Pointwise Mutual Information) نیز می‌گویند.

$$\large SI(x,y)=\log {\frac {p(x,y)}{p(x)\,p(y)}}$$

یکی از خصوصیات اصلی برای اطلاع متقابل وجود رابطه زیر است. به این ترتیب مقدار $$I(X;Y)$$ مشخص می‌کند که اطلاع از $$Y$$ بطور متوسط به چه میزان می‌تواند در میزان اطلاعات $$X$$ نقش داشته باشد. در صورتی که هدف کد کردن $$X$$ باشد، مقدار $$I(X;Y)$$ میانگین بیت‌های صرفه‌جویی شده در حالتی را نشان می‌دهد که از $$Y$$ آگاهی داریم. تعداد این بیت‌ها بطور معمول کمتر از حالتی است که بدون اطلاع از $$Y$$ بخواهیم $$X$$ را کد کنیم.

یکی دیگر از خصوصیات جالب MI، وجود تقارن در آن است زیرا مشخص است که $$SI(x,y)=SI(y,x)$$ و به این ترتیب می‌توان نوشت:

$$\large I(X;Y)=I(Y;X)$$

به این ترتیب با توجه به رابطه اخیر و بی‌نظمی شرطی، خواهیم داشت.

$$\large I(X;Y)=I(Y;X)=H(X)+H(Y)-H(X,Y)$$

از طرفی MI را برحسب امید ریاضی «واگرایی کولبک-لیبلر» (Kullback-Leibler Divergence) بین توزیع پسین $$X$$ به شرط $$y$$ و پیشین $$x$$ نیز می‌توان نوشت:

$$\large I(X;Y)=I(X;Y)=\mathbb {E} _{p(y)}[D_{\mathrm {KL} }(p(X|Y=y)\|p(X))]$$

به بیان دیگر، این مقدار نشان می‌دهد که بطور متوسط تابع احتمال $$X$$ با آگاهی از $$Y$$ به چه میزان نسبت به عدم آگاهی تغییر می‌کند.

مفهوم آماری «آزمون نسبت درستنمایی» (Log-Likelihood Ratio Test) بسیار با MI بخصوص در زمینه‌های «جداول توافقی» (Contingency Tables)، «توزیع‌ چندجمله‌ای» (Mutinomial Distribution) و «آماره کای ۲ پیرسون و آزمون آن» (Perason's $$\chi^2$$ Test) در رابطه است به شکلی که از MI می‌توان برای مشخص کردن استقلال دو متغیر تصادفی استفاده کرد.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش تئوری آشکارسازی (Detection Theory)
• مجموعه آموزش‌های داده کاوی و یادگیری ماشین
• آنتروپی اطلاعات — مبانی اولیه
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده
• متغیر تصادفی، تابع احتمال و تابع توزیع احتمال

^^