توزیع های آماری گاما و بتا — مفاهیم و کاربردها

در آمار و تئوری احتمالات، توزیع گاما (Gamma Distribution) جزء توابع توزیع دو پارامتری بوده و از اهمیت خاصی برخوردار است. برای مثال تابع توزیع نمایی و کای-۲ حالت خاصی از توزیع گاما محسوب می‌شوند. بنابراین به نظر می‌رسد که باید کاربردهای متعددی برای متغیر تصادفی با این توزیع وجود داشته باشد. از طرف دیگر استفاده از توزیع بتا (Beta Distribution) نیز در بسیاری از موارد بخصوص استنباط بیزی می‌تواند به عنوان مزدوج توزیع به کار رود. بنابراین آگاهی از خصوصیات آن می‌‌تواند در حل بسیاری از مسائل استنباط آماری موثر باشد.

از آنجایی که در این نوشتار از متغیر تصادفی و تابع احتمال صحبت به میان خواهد آمد بهتر است ابتدا مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کرده باشید. همچنین اگر به تابع گاما (Gamma Function) و خصوصیات آن علاقه‌مند باشید می‌توانید مطلب اصول شمارش و فاکتوریل — به زبان ساده و اگر می‌خواهید از کاربردهای توزیع کای-۲ نیز مطلع شوید مطلب آزمون‌ نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای۲ را بخوانید.

تابع توزیع گاما (Gamma Distribution Function)

این تابع توزیع را می‌توان با پارامترهای «شکل» (Shape Parameter) و «معکوس-مقیاس» (Inverse Scale Parameter) نشان داد.

فیلم آموزش کنترل کیفیت آماری – جامع و با نکات کاربردی در فرادرس

کلیک کنید

در این حالت $$\alpha$$ را پارامتر شکل و $$\beta$$ را معکوس-مقیاس می‌نامند. اگر X یک متغیر تصادفی با توزیع گاما باشد می‌نویسند:

$$\large X \sim \Gamma(\alpha,\beta)$$

تابع چگالی احتمال برای این متغیر تصادفی براساس پارامترهای $$\alpha$$ و $$\beta$$ به صورت زیر است:

$$\large f(x;\alpha,\beta)=\dfrac{\beta^{\alpha}x^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)}$$

که در آن x>0 و $$\alpha , \beta$$ مقدارهایی مثبت و $$\Gamma(\alpha)$$ نیز مقدار تابع گاما در نقطه $$\alpha$$ است. با توجه به این تعریف مشخص است که تکیه‌گاه این متغیر تصادفی مقدارهای مثبت خواهد بود.

نکته: گاهی تابع چگالی این متغیر تصادفی را برحسب پارامترهای «شکل» ($$\kappa$$) و «مقیاس» ($$\theta$$) بیان می‌کنند و می‌نویسند:

$$\large f(x;\kappa,\theta)=\dfrac{x^{\kappa -1}e^{\frac{-x}{\theta }}}{\theta^{\kappa}\Gamma(\kappa)}$$

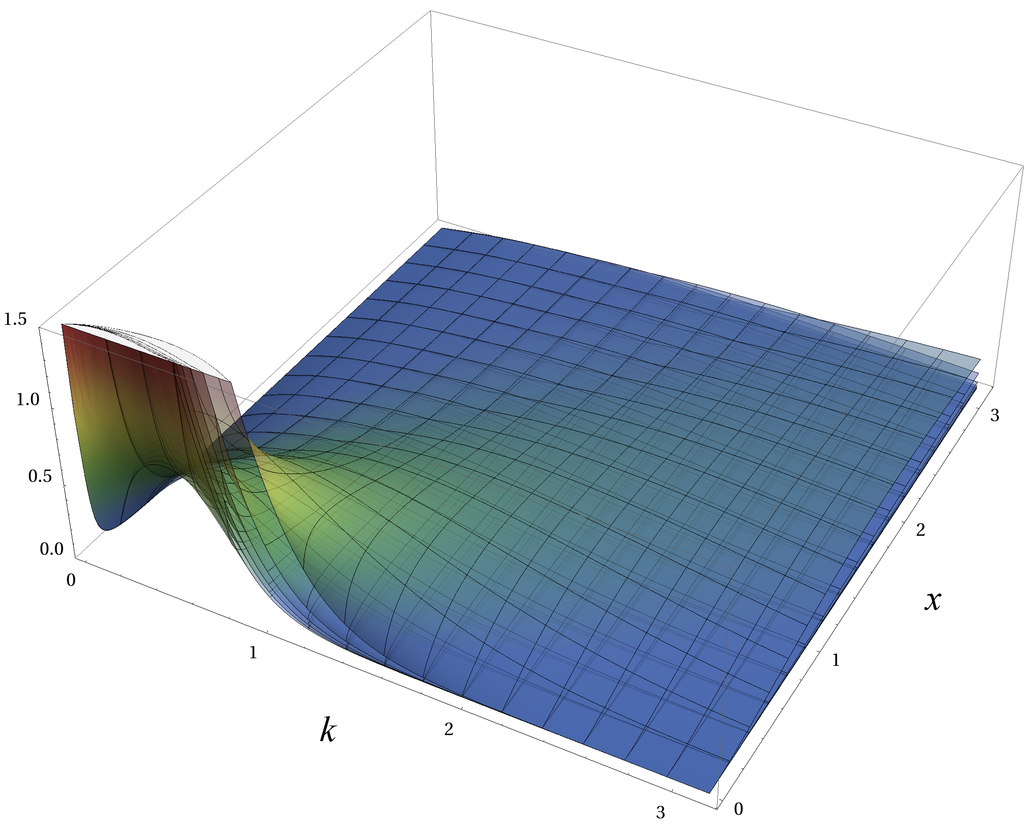
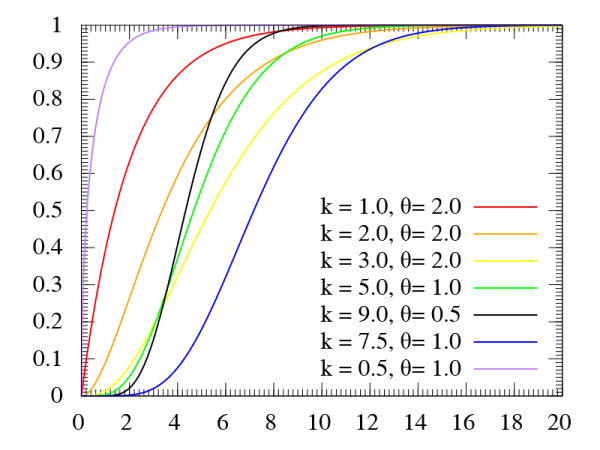
واضح است که در این حالت $$\kappa=\alpha$$ و $$\beta=1/\theta$$ خواهد بود. براساس این تابع چگالی تصاویر زیر، نشان دهنده تابع احتمال و تابع احتمال توزیع تجمعی براساس مقدارهای مختلف پارامترها شکل ($$\kappa$$) و مقیاس ($$\theta$$) است.

البته برای نمایش نمودارهای مربوط به تابع چگالی متغیر تصادفی گاما، برحسب هر دو پارامتر، مجبور به ترسیم منحنی‌ها به صورت سه بعدی هستیم. در تصویرهای زیر این حالت در نظر گرفته شده است و به ازای مقدارهای مختلف x و پارامتر شکل $$\kappa$$ نمودارهای مختلف به تفکیک برای $$\theta = 0.25,0.5,0.75,1,2,3$$ ترسیم شده است.

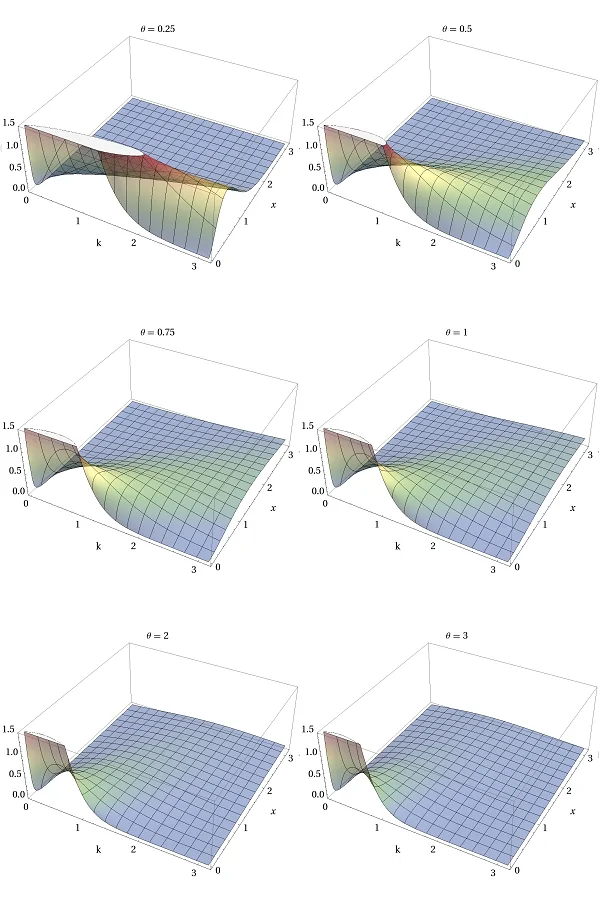
امید ریاضی و واریانس توزیع گاما

از آنجایی که دو شیوه برای بیان تابع چگالی احتمال این متغیر تصادفی وجود دارد، امید ریاضی و واریانس آن نیز به دو شکل نمایش داده می‌شود. در جدول زیر این نحوه محاسبات براساس این دو نوع نگارش تابع چگالی می‌بینیم.

از آنجایی که مقدار پارامتر شکل ($$\alpha,\;\kappa$$) مثبت است، باید منحنی تابع چگالی این متغیر تصادفی دارای چولگی مثبت باشد و به بیان دیگر دم منحنی به سمت راست کشیده‌تر دیده می‌شود. البته دیده می‌شود که با افزایش این پارامتر، شکل منحنی به توزیع نرمال نزدیک خواهد شد.

خصوصیات توزیع گاما

توزیع گاما دارای ویژگی‌ها و خصوصیات جالبی است. در ادامه به بررسی این ویژگی‌ها می‌پردازیم:

• حاصل جمع متغیرهای تصادفی $$X_i$$ با توزیع گاما با پارامتر شکل $$\kappa_i$$ و پارامتر ثابت مقیاس $$\theta$$ نیز دارای توزیع گاما خواهد بود. یعنی می‌توان نوشت: $$\sum_{i=1}^n X_i\sim \Gamma (\sum_{i=1}^n \kappa_i,\theta)$$
• اگر $$X\sim \Gamma(\kappa,\theta)$$، برای مقدار ثابت و مثبت c داریم: $$cX\sim \Gamma(\kappa,c\theta)$$ یا به عبارت دیگر $$cX\sim \Gamma (\alpha,\dfrac{\beta}{c})$$.
• متغیر تصادفی نمایی با میانگین $$\theta$$ همان متغیر تصادفی با توزیع گاما با پارامترهای $$\kappa=1$$ و $$\theta$$ است. یعنی $$X\sim E(\theta)\equiv X\sim \Gamma(1,\theta)$$.
• اگر $$X\sim \Gamma(v/2,2)$$ (براساس پارامتر شکل و مقیاس) آنگاه می‌توان X را دارای توزیع کای-۲ دانست. یعنی $$X\sim \Gamma(v/x,2)\equiv \chi^2(v)$$.
• اگر $$X\sim \Gamma(\alpha,\theta)$$ و $$Y\sim \Gamma(\beta,\theta)$$ و مستقل از یکدیگر باشند، آنگاه $$\dfrac{X}{X+Y}$$ دارای توزیع Beta با پارامترهای $$\alpha,\beta$$ است.
• تابع توزیع گاما در بحث استنباط بیزی می‌تواند به عنوان مزدوج پیشین برای بسیاری از توزیع‌ها از جمله پواسن، نمایی، نرمال (با معلوم بودن میانگین) و حتی خود توزیع گاما با معلوم بودن پارامتر شکل (Shape Parameter) به کار رود.

استفاده از اکسل برای محاسبه تابع توزیع احتمال و صدک‌های توزیع گاما

معمولا برای محاسبه تابع چگالی یا چندک‌های توزیع‌های آماری از جدول‌های آماده یا نرم‌افزارهای آماری استفاده می‌شود. در اینجا با استفاده از اکسل به محاسبه این مقدارها می‌پردازیم. به این منظور جدول زیر برای معرفی توابع اکسل مرتبط با توزیع گاما تهیه شده است.

برای مثال اگر بخواهیم مقدار توزیع احتمال تجمعی گاما با پارامترهای $$\alpha=1$$ و $$\beta=2$$ را در نقطه x=0.5 پیدا کنیم از دستور زیر استفاده خواهیم کرد:

$$=GAMMA.DIST(0.5,1,2,TRUE)=0.221199$$

و برعکس اگر به صدک 22ام توزیع گاما با پارامترهای ۱ و ۲ احتیاج داشته باشید، کافی است تابع زیر را در یک سلول اکسل وارد کنید.

$$=GAMMA.INV(0.22,1,2)=0.496923$$

همانطور که دیده می‌شود نتیجه‌های حاصل شده از تابع احتمال تجمعی با صدک ۲۲ام مطابقت دارد.

تابع توزیع بتا (Beta Distribution Function)

تابع توزیع بتا (Beta Distribution) یکی از توزیع‌های احتمالی است که روی فاصله ۰ تا ۱ تعریف شده است. این توزیع بخصوص در بحث مربوط به آماره‌های ترتیبی و توزیع آن‌ها برای متغیرهای تصادفی یکنواخت اهمیت پیدا می‌کند. همچنین در بسیاری از موارد بخصوص در استنباط آماری بر پایه بیز (Bayesian Inference) از توزیع بتا به عنوان توزیع پیشین توزیع دو جمله‌ای برای برآورد بیزی پارامتر احتمال موفقیت استفاده می‌شود.

فیلم آموزش توزیع نرمال در آمار و کاربرد آن در علوم انسانی (رایگان) در فرادرس

کلیک کنید

پارامترهای این توزیع با $$\alpha$$ و $$\beta$$ به عنوان پارامترهای «شکل» (Shape Parameter) مشخص می‌شود. در بسیاری از موارد که باید مقدار متغیر تصادفی در فاصله ۰ تا ۱ باشد از توزیع بتا استفاده می‌شود. البته توزیع‌های دیگری مانند توزیع یکنواخت در فاصله ۰ و ۱ نیز به کار می‌آیند.

اگر متغیر تصادفی X دارای توزیع بتا باشد، آن را به صورت زیر نشان می‌دهیم.

$$\large X\sim Beta(\alpha,\beta)$$

مشخص است که در این حالت پارامترهای این توزیع مثبت بوده و داریم $$0\leq X\leq 1$$. شکل تابع چگالی احتمال برای این متغیر تصادفی به صورت زیر نوشته می‌شود:

$$\large f(x;\alpha,\beta)=\dfrac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0^1 u^{\alpha-1}(1-u)^{\beta-1}}du=$$

$$\large \dfrac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{(\alpha-1)}(1-x)^{(\beta-1)}=$$

$$\large \dfrac{1}{Beta(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}$$

واضح است که منظور از $$Beta(\alpha,\beta)$$ نسبت دو مقدار تابع گاما است. یعنی می‌توان تساوی زیرا را برحسب تابع گاما و بتا بررسی کرد:

$$\large Beta(\alpha,\beta)=\dfrac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$$

این کسر را تابع Beta می‌نامند.

همچنین قابل ذکر است که با برابر بودن مقدار x  با ۰ یا ۱، تابع چگالی برابر با صفر می‌شود. ولی برای بقیه نقاط در فاصله ۰ تا ۱ مقدار تابع چگالی غیرصفر خواهد بود. شکل تابع چگالی احتمال این متغیر تصادفی در تصویر زیر دیده می‌شود.

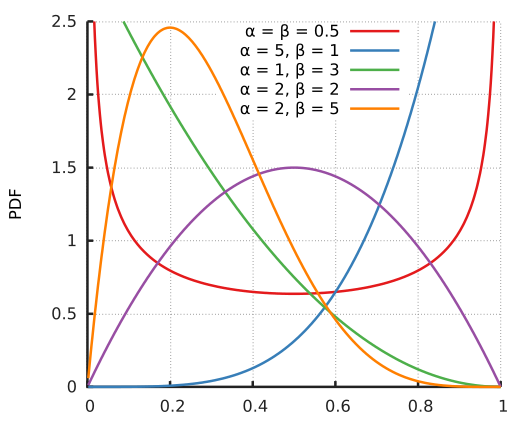
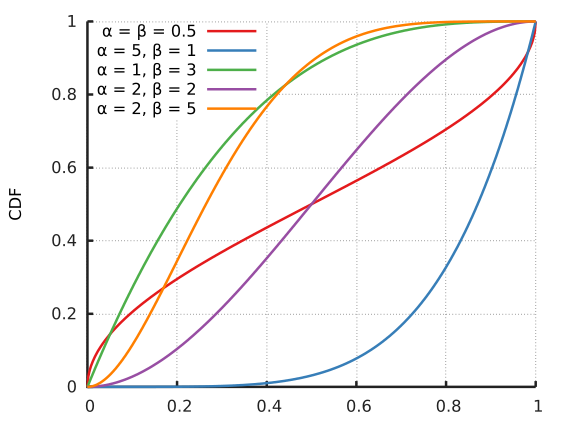
همانطور که در شکل اول دیده می‌شود، اگر پارامترهای شکل تابع توزیع بتا از ۱ کوچکتر باشند، نمودار در نقطه ۰ و ۱ دارای شکست خواهد شد و به نظر پیوسته نخواهد بود. ولی در بقیه حالات پیوستگی تابع چگالی مشخص است. از طرف دیگر با بزرگ شدن پارامترهای شکل در توزیع بتا، نمودار تابع چگالی به نرمال نزدیک خواهد شد.

امید ریاضی و واریانس توزیع بتا

با توجه به تابع چگالی و خصوصیات متغیر تصادفی بتا، امید ریاضی برای این توزیع به صورت زیر درخواهد آمد:

$$\large E(X)=\dfrac{\alpha}{\alpha+\beta}$$

همچنین واریانس نیز براساس رابطه زیر محاسبه خواهد شد:

$$\large Var(X)=\dfrac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$$

خصوصیات توزیع بتا

با توجه به شکل تابع چگالی این توزیع می‌توان دریافت که:

• اگر $$X\sim Beta(\alpha,\beta)$$ آنگاه $$1-x\sim Beta(\beta,\alpha)$$.
• اگر $$X\sim Beta(n/x,m/x)$$ آنگاه $$\dfrac{mX}{n(1-X)}\sim F(n,m)$$ که منظور از $$F(n,m)$$ توزیع F با پارامترهای n و m است.
• اگر $$X\sim Beta(\alpha,1)$$ آنگاه $$-ln(X)\sim E(\alpha)$$ است. منظور از $$E(\alpha)$$ توزیع نمایی با پارامتر $$\alpha$$‌ است.
• اگر $$X\sim Beta(1,1)$$ آنگاه $$X\sim U(0,1)$$ است. یعنی متغیر تصادفی با توزیع یکنواخت در فاصله ۰ تا ۱ همان توزیع بتا با پارامترهای ۱ و ۱ است.

همانطور که گفته شد، متغیر تصادفی با توزیع بتا دارای تکیه‌گاه در فاصله ۰ تا ۱ (باز یا بسته) است. ولی با استفاده از یک انتقال و تغییر مقیاس می‌توان تابع توزیع بتا چهار پارامتری تولید کرد که تکیه گاه آن در فاصله A تا B قرار داشته باشد. در این حالت اگر Y متغیر تصادفی بتا با چهار پارامتر باشد و X نیز با توزیع بتای دو پارامتری (در فاصله ۰ تا ۱) می‌توان رابطه زیر را برقرار کرد:

$$\large Y=X(B-A)+A$$

آنگاه توزیع Y را به صورت $$Beta(\alpha,\beta,A,B)$$ نشان می‌دهند. در این صورت شکل تابع چگالی احتمال طبق رابطه زیر نوشته می‌شود:

$$\large \displaystyle f(y;\alpha ,\beta ,A,B)={\frac {f(x;\alpha ,\beta )}{B-A}}={\frac {\left({\frac {y-A}{B-A}}\right)^{\alpha -1}\left({\frac {B-y}{B-A}}\right)^{\beta -1}}{(B-A)Beta(\alpha ,\beta )}}=$$

$$\large \displaystyle \frac {(y-A)^{\alpha -1}(B-y)^{\beta -1}}{(B-A)^{\alpha +\beta -1}Beta(\alpha ,\beta )}$$

نکته: با توجه به این شکل از تابع چگالی، مشخص است که متغیر تصادفی Y در فاصله A تا B تغییر می‌کند. A را کران پایین و B را کران بالای توزیع بتای چهار پارامتری گویند.

استفاده از اکسل برای محاسبه تابع توزیع احتمال و صدک‌های توزیع بتا

برای محاسبه روی توزیع بتا لازم است که انتگرال‌های مربوط به تابع چگالی را محاسبه کرد. البته روش‌های عددی برای بدست آوردن مقدار انتگرال در چنین مواقعی بسیار مفید هستند.

فیلم آموزش محاسبات آماری در اکسل Excel در فرادرس

کلیک کنید

همچنین نرم‌افزارهای آماری به خوبی از عهده این کار بر می‌آیند. ولی در اینجا برای محاسبه تابع چگالی یا چندک‌های توزیع‌های آماری بتا از اکسل استفاده می‌کنیم. در ادامه با توابعی از اکسل آشنا می‌شویم که به این منظور به کار می‌آیند. جدول زیر به معرفی توابع اکسل مرتبط با توزیع بتا می‌پردازد.

برای مثال اگر بخواهیم مقدار توزیع احتمال تجمعی بتا با پارامترهای $$\alpha=1$$ و $$\beta=2$$ را در نقطه x=0.5 پیدا کنیم از دستور زیر استفاده خواهیم کرد:

$$\large =BETA.DIST(0.5,1,2,TRUE)=0.75$$

و برعکس اگر به صدک 75ام توزیع بتا با پارامترهای ۱ و ۲ احتیاج داشته باشید، کافی است تابع زیر را در یک سلول اکسل وارد کنید.

$$\large =‌BETA.INV(0.75,1,2)=0.5$$

همانطور که دیده می‌شود نتیجه‌های حاصل شده از تابع احتمال تجمعی با صدک 75ام مطابقت دارد.

نکته: باید توجه داشته باشید که در هنگام استفاده از توابع BETA.DIST و BETADIST، مقدار x باید یا در فاصله ۰ تا ۱ باشد و یا اگر پارامترهای A و B‌ معرفی شده‌اند، در فاصله بین آن دو قرار بگیرد. در ضمن مقدار Probability نیز حتما باید بین ۰ تا ۱ (برای معرفی صدک‌ها) باشد.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آزمایش تصادفی، پیشامد و تابع احتمال
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده
•  تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
• متغیر تصادفی و توزیع نمایی — به زبان ساده

^^