مفاهیم تابع – به زبان ساده
هر تابعی یک ورودی را به یک خروجی ربط میدهد. تابع همانند ماشینی است که یک ورودی و یک خروجی دارد. در تابع، خروجی به طریقی به ورودی وابسته است. یک تابع معمولاً به صورت (f(x نوشته میشود. بدین ترتیب «... = (f(x» یک روش کلاسیک برای نوشتن تابع است و همانطور که در ادامه خواهید دید، روشهای دیگری نیز برای نوشتن تابع وجود دارند. البته توجه داشته باشید در برخی مواقع میتوان از یک تابع بهعنوان ورودی تابعی دیگر استفاده کرد. در این حالت اصطلاحا تابعی ترکیبی را تولید کردهایم.

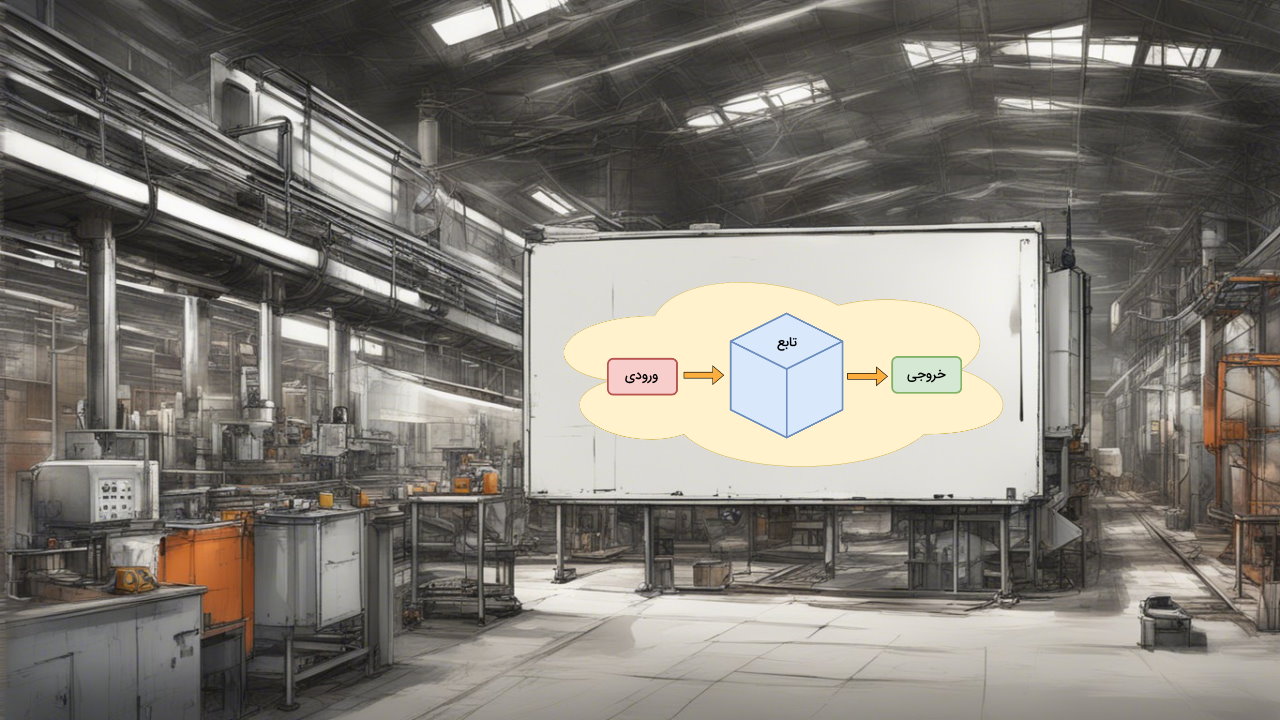
ورودی، ضابطه، خروجی
چندین روش برای درک توابع وجود دارد؛ ولی در هر صورت، این سه بخش همیشه در یک تابع وجود دارند:
- ورودی
- ضابطه
- خروجی
مثال: «ضرب در 2» یک تابع بسیار ساده است.
سه بخش تابع اینجا نوشته شده اند:
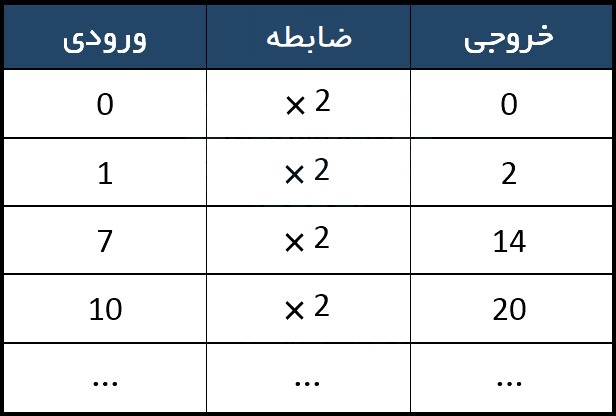
آیا می توانید بگویید برای یک ورودی 50، خروجی چیست؟
برخی از مثالهای تابع
- x2 (مربع کردن) یک تابع است.
- X3 + 1 نیز یک تابع است.
- سینوس، کسینوس و تانژانت نیز توابع مورد استفاده در مثلثات هستند.
- و ...
اما ما در این نوشته از مجله فرادرس قصد نداریم تابع خاصی را مورد مطالعه قرار دهیم و به جای آن تابع را با نگاهی عمومی بررسی میکنیم.
نامها
در ابتدا بهتر است برای هر تابع یک نام تعیین کنیم. معمول ترین اسم f است، اما میتوانیم نامهای دیگری همچون g روی تابع بگذاریم. هر چند هر نامی میتوان روی تابع گذاشت؛ ولی بهتر است از حروف کوچک انگلیسی استفاده شود.
به تصویر زیر توجه کنید:

در مود تابع فوق میگوییم "افِ ایکس (f(x برابر است با مربع x". آنچه که وارد تابع میشود، درون پرانتز ( ) بعد از نام تابع قرار میگیرد. پس (f(x به ما میگوید که نام تابع "f" است و "x" وارد تابع میشود. معمولاً میخواهیم بدانیم که یک تابع با ورودی خود چه میکند:
f(x) = x2
به ما نشان می دهد که تابع f، مقدار ورودی x را گرفته و آن را مربع میکند.
مثال: با تابع زیر:
f(x) = x2
- یک ورودی 4
- به خروجی 16 تبدیل میشود
در واقع میتوان نوشت: f(4) = 16
در توابع ترکیبی بهجای x میتواند تابعی دیگر همچون (g(x وجود داشته باشد.
x فقط یک نماد است
زیاد نگران x در مقابل نام تابع نباشید، چون به این دلیل آنجا نوشته شده است که فقط به ما نشان دهد ورودی به کجا میرود و چه اتفاقی برای آن میافتد. این مقدار x میتواند هر چیزی باشد.
به جای x هر چیزی دیگری میتوانیم بنویسیم. پس این تابع f(x) = 1 - x + x2 همان تابعهای زیر است:
f(q) = 1 - q + q2
h(A) = 1 - A + A2
w(θ) = 1 - θ + θ2
متغیر ( x, q, a, …) آنجاست که بدانیم عدد مورد نظر را کجا قرار خواهیم داد:
f(2) = 1 - 2 + 22 = 3
گاهی اوقات تابع اسمی ندارد و به شکل زیر است:
y = x2
اما هنوز این موارد را داریم:
- یک ورودی (x)
- یک ضابطه (مربع کردن)
- یک خروجی (y)
ارتباط
در ابتدای متن گفتیم که یک تابع همانند یک دستگاه عمل میکند. اما یک تابع در واقع تسمه یا چرخ دنده یا قسمت متحرک دیگری ندارد. در حقیقت هر چه در آن میگذاریم، نابود نمیشود. یک تابع یک ورودی را به یک خروجی نسبت میدهد. هنگامی که گفته میشود:
f(4) = 16
به این معنی است که عدد 4 به نحوی با 16 در ارتباط است. یا: 4 → 16
مثال:
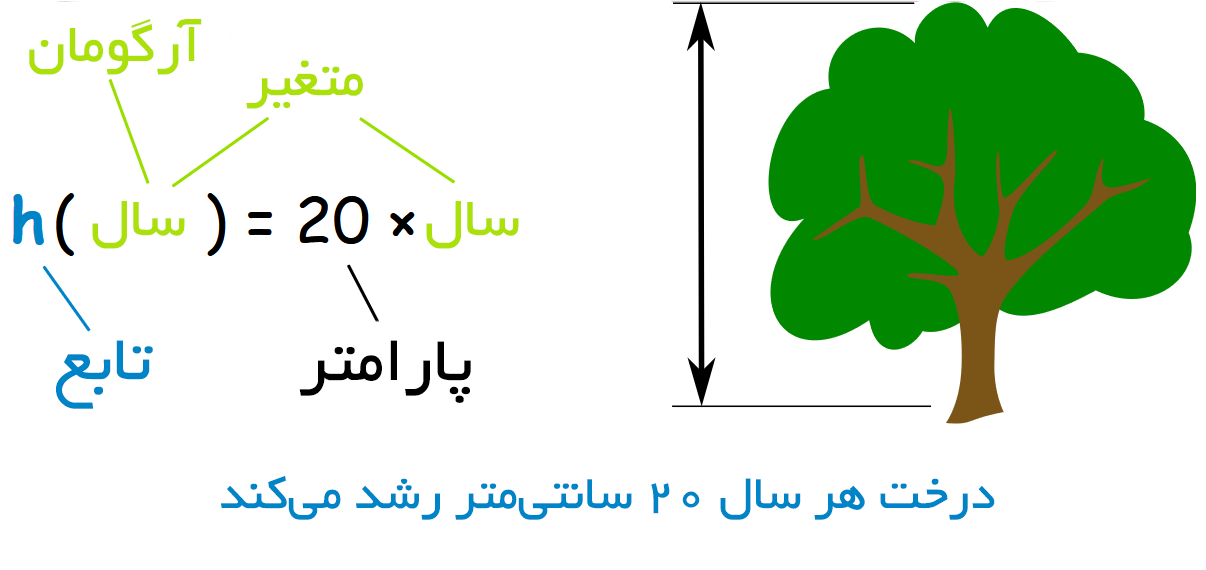
فرض کنید این درخت هر سال، 20 سانتی متر قد میکشد، پس ارتفاع درخت به سن آن وابسته است. در تابع h میبینیم:
20 × سن = (سن) h
پس، اگر سن درخت 10 سال باشد، ارتفاع برابر خواهد بود با:
h (10) = 10 × 20 = 200 cm
اینجا چند مقدار را به طور مثال می بینید:
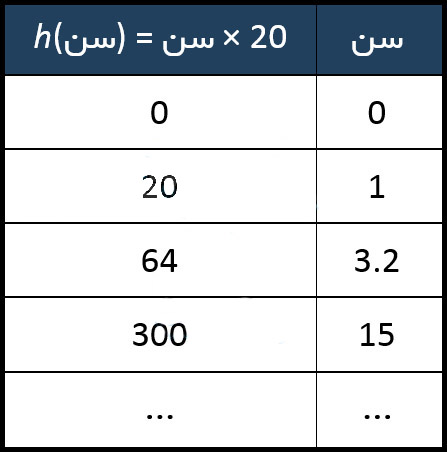
تابع چه نوع چیزهایی را پردازش میکند؟
بدیهی است که تابع اعداد را پردازش میکند؛ اما سوال این است که چه نوع اعداد؟ برای مثال، تابع ارتفاع درخت برای سن زیر 0 بیمعنی خواهد بود. همچنین ورودی تابع میتواند حروف (B → A)، یا کدهای شناسایی (وارد شو → A6309) یا حتی چیزهای عجیبتری نیز باشد.
پس ما به ورودی قدرتمندتری احتیاج داریم، و اینجاست که مجموعهها وارد عمل میشوند:
یک مجموعه، دسته ای از اشیا است.
چند مثال از مجموعهها را میبینیم:
- مجموعه اعداد زوج: { …, -4, -2, 0, 2, 4, …}
مجموعه لباس ها: { "کلاه"، "پیراهن"،...}
مجموعه اعداد اول: {2, 3, 5, 7, 11, 13, 17, …}
مضرب های مثبت 3 که کمتر از 10 هستند: {3, 6, 9}
به هر شئ در داخل مجموعه (همانند «4» یا «کلاه»)، یک عضو گفته میشود. پس، یک تابع اعضای یک مجموعه را می گیرد، و سپس اعضای یک مجموعه دیگر را باز میگرداند.
تابع قاعد خاصی دارد
یک تابع قوانین ویژهای دارد:
- تابع همواره باید به همه ورودیهای ممکن پاسخ دهد
- و تنها برای هر ورودی نیز تنها یک رابطه خواهد داشت.
این قوانین می توانند در یک جمله نوشته شوند:
تعریف رسمی یک تابع
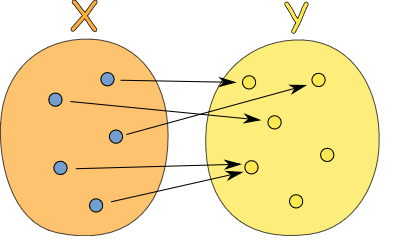
یک تابع هر عضو یک مجموعه را دقیقا با یک عضو از یک مجموعه دیگر مرتبط میکند (امکان دارد همان مجموعه باشد).
دو نکته مهم
1- عبارت «هر عضو...» به این معنی است که هر عضو در مجموعه X به برخی اعضای مجموعه Y مرتبط است. میگوییم که تابع، مجموعه X را پوشش میدهد، یعنی تمامی اعضای آن را مرتبط می کند. اما برخی از اعضای Y ممکن است کلا مرتبط نباشند، که ایرادی ندارد.
2- عبارت «دقیقا یک...» به این معنی است که یک تابع تک مقداری است. پس برای یک ورودی، 2 نتیجه یا بیشتر نخواهد داد.
بنابراین تابعی به شکل زیر در ریاضیات وحود ندارد:
9 یا 7 = (2)f
نکته: «یک به چند» مجاز نیست؛ اما «چند به یک» مجاز است:
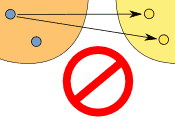
(یک به چند) این در یک تابع مجاز نیست | 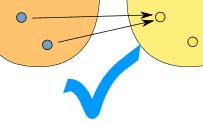
(چند به یک) اما این در توابع مجاز است |
اگر یک رابطه از دو قانون بالا پیروی نکند، این رابطه یک تابع نیست. در واقع همچنان یک رابطه هست؛ اما تابع محسوب نمیشود.
مثال: رابطه x → x2
می توان آن را در جدول نیز نوشت:
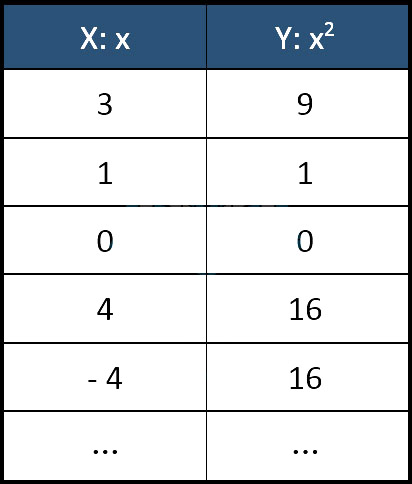
این یک تابع است، چون:
- هر عضو در X به عضوی در Y مرتبط است
- هیچ عضوی در X شامل دو یا چند رابطه نیست
پس از قوانین تابع پیروی می کند. دقت کنید که چگونه هر دو عدد 4 و 4- با 16 در ارتباط هستند، و این ارتباط مجاز است.
مثال: این رابطه یک تابع نیست:

این یک رابطه است؛ اما یک تابع نیست، چون که:
- مقدار 3 در X رابطهای با Y ندارد
- مقدار 4 در X رابطهای با Y ندارد
- مقدار 5 با بیش از یک مقدار در Y ارتباط دارد
اما این مسئله که 6 در Y رابطهای ندارد به تابع نبودن کمکی نمیکند.
آزمایش با یک خط عمودی
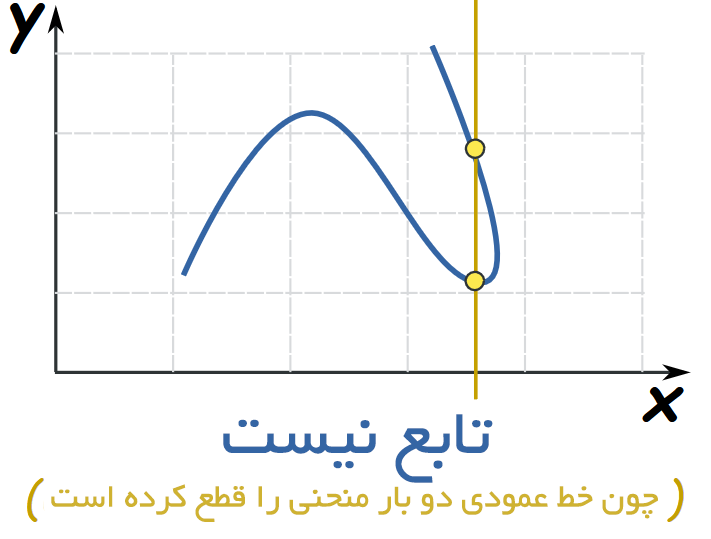
روی یک نمودار، تک مقداری به این معنی است که هر خط عمودی، منحنی را هیچگاه بیش از یک بار قطع نمیکند. اگر بیش از یک بار قطع کند، همچنان یک منحنی است، اما تابع نیست. برخی از انواع توابع وجود دارند که قوانین سختتری دارند، برای مثال میتوان به توابع یکبهیک اشاره نمود.
تعداد اعضای بسیار زیاد
در این مثالها تنها چند مقدار دیدید، اما توابع معمولاً بر اساس مجموعه هایی با عضوهای بینهایت زیاد کار میکنند.
مثال:
y = x3
- مجموعه ورودیهای «X» تمامی اعداد حقیقی است
- مجموعه خروجیهای «Y» نیز تمامی اعداد حقیقی است
در این مورد نمیتوانیم تمامی مقدارها را نشان دهیم. پس چند تا از مقدارها را بعنوان مثال مینویسیم:
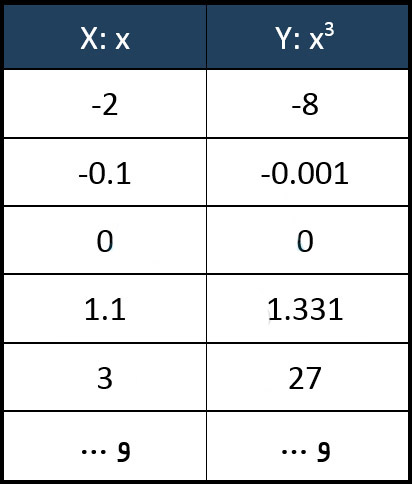
دامنه، هم دامنه و برد
در مثال های بالا:
- مجموعه «X» دامنه،
- مجموعه «Y» هم دامنه، و
- مجموعه اعضایی که در Y مرتبط شدهاند (مقدارهای بدست آمده از یک تابع)، برد نامیده میشوند.
این موضوع به صورت دقیق در مطلب «دامنه و برد تابع — به زبان ساده» از مجله فرادرس مورد بررسی قرار گرفته است.
عناوین زیاد برای تابعهای مختلف
توابع در ریاضیات به مدت زیادی است که استفاده میشوند، و نامها و روشهای مختلفی برای نوشتن توابع وجود دارد. در ادامه برخی از اصطلاحات معمولتر را که باید با آنها آشنا شوید ارائه میکنیم:
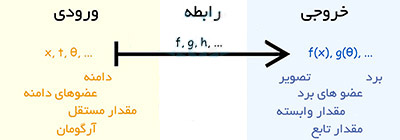
مثال: در تابع زیر
z = 2u3
- «u» می تواند «متغیر مستقل» نامیده شود
- «z» می تواند «متغیر وابسته» (که وابسته به مقدار u است) نامیده شود
مثال: در تابع زیر
f(4) = 16
- "4" می تواند "آرگومان" نامیده شود
- "16" نیز می تواند "مقدار تابع" نامیده شود
زوجهای مرتب
زوج مرتب روشی دیگر برای نوشتن مقادیر تابع است. ورودی و خروجی یک تابع را میتوان به صورت یک «زوج مرتب» نوشت. همانند (4,16) به این زوجها مرتب گفته میشود، چون ورودی همواره در اول و خروجی به عنوان عبارت دوم میآید:(خروجی, ورودی). پس به این شکل خواهد بود:
(x, f(x))
مثال:
(4,16) به این معنی است که تابع مقدار 4 را میگیرد و 16 را در پاسخ میدهد.
مجموعه زوجهای مرتب
یک تابع میتواند به شکل مجموعهای از زوجهای مرتب باشد:
مثال:
{(2,4), (3,5), (7,3)}
تابعی است که میگوید «2 به 4 مربوط است»، «3 به 5 مربوط است» و «7 به 3 مربوط است».
همچنین، به یاد داشته باشید که:
- دامنه برابر {7 ,3 ,2} است (مقادیر ورودی)
- و برد برابر {3 ,5 ,4} است (مقادیر خروجی)
اما تابع باید تک مقداری باشد، پس همچنین میتوانیم بگوییم:
"اگر شامل (a,b) و (a,c) باشد، پس b باید با c برابر باشد"
که منظور آن این است که ورودی a نمیتواند دو نتیجه متفاوت داشته باشد.
مثال:
{(2,4), (2,5), (7,3)}
این مجموعه یک تابع نیست چرا که {2,4} و {2,5} به این معنی است که 2 میتواند به 4 یا 5 مرتبط باشد. به عبارتی دیگر این مجموعه تابع نیست، چون تک مقداری نیست.
مزیت زوجهای مرتب
می توانیم نمودار آنها را رسم کنیم.
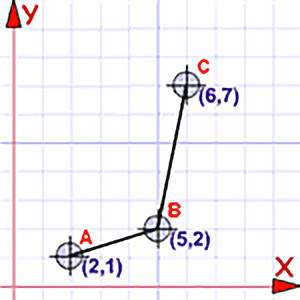
چرا که اینها مختصات نیز هستند. پس یک مجموعه از مختصات نیز در صورتی که قوانین بالا را رعایت کند، یک تابع است.
یک تابع میتواند قسمتهای مختلفی داشته باشد
میتوانیم توابعی بسازیم که نسبت به مقدار ورودی، عکسالعمل متفاوتی نشان دهند.
مثال: یک تابع با دو قسمت:
- هنگامی که x کمتر از 0 است، خروجی 5 است
- هنگامی که x بزرگتر یا مساوی 0 است، خروجی x2 است.
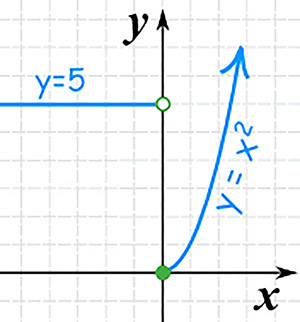
برخی از اعداد:
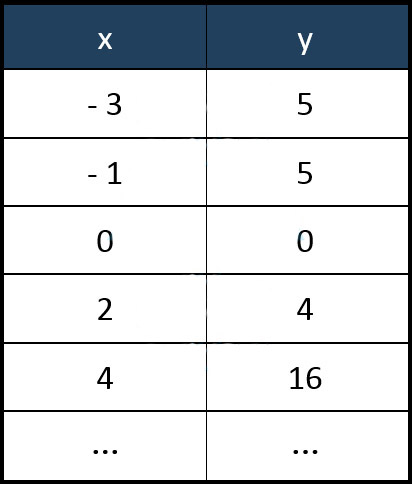
تابع صریح در مقابل تابع ضمنی
آخرین موضوعی که در خصوص تابعهای بررسی میکنیم، توابع صریح و ضمنی هستند. به یک تابع زمانی صریح میگوییم که دقیقاً به ما نشان دهد چگونه از x به y می رویم، مانند:
y = x3 – 3
در این وضعیت اگر x را بدانیم، می توانیم y را بیابیم. این همان مدل کلاسیک تابع زیر است.
y = f(x)
تابع ضمنی تابعی است که به طور مستقیم ارائه نمیشود مانند:
x2 - 3xy + y3 = 0
در تابع فوق اگر x را بدانیم، y را چگونه مییابیم؟ شاید سخت و یا حتی غیر ممکن باشد که مستقیماً از x به y برسیم. اصطلاح «ضمنی» از "واژه ضمن عریی گرفته شده که به معنی غیر مستقیم است. در آینده در مورد رسم توابع چند جملهای نیز صحبت خواهیم کرد.
نتیجه گیری
- یک تابع ورودی را به خروجی ربط میدهد.
- یک تابع اعضا را از یک مجموعه (دامنه) گرفته و آنها را به اعضای یک مجموعه دیگر (شاید همان مجموعه) ربط میدهد (هم دامنه).
- تمامی خروجیها (مقادیری که به آن مقدارهای دیگری مرتبط شدهاند) کلاً بُرد نامیده میشوند
- یک تابع نوعی رابطه ویژه است که: 1) هر عضو در دامنه را شامل میشود و 2) هر ورودی تنها یک خروجی تولید میکند
- یک ورودی و خروجی مرتبط با آن، در مجموع زوج مرتب نامیده میشوند
- یک تابع همچنین میتواند به عنوان مجموعه زوجهای مرتب نیز نمایش داده شود.
در آینده در مورد دیگر مفاهیم مرتبط با تابع همچون نقطه عطف و ماکزیمم و مینیمم آن بحث خواهیم کرد.












خیلی عالی و مفهومی بودش
خدا خیرتون بده❤
باورم نميشه انقدر بي نظير و بي عيب و نقض توضيح بدين واقعا اگر تمام مدارس ايران مثل شما ها اموزش بدن همه دكتر حسابي ميشن . به نظر شخصي من هر فردي توان انجام يه كاري و داره و هر كسي هم معلم نميشه معلم بودن يكي از سخت ترين شغل دنياست و من افتخار ميكنم بهتون كه از پس سخترين كار دنيا به اسوني بر مياييد.
حتی از معلممون بهتر توضیح داده شده بود.مرسی
سلام. دمتون گرم
شیر مادر و نان پدر حلالت
خیلی عالی بود با فرادرس نیاز به کلاس نیست😂
منم کلاس هشتمم و واقعا خیلی ساده توضیح داده بودین!
فوق العاده ساده و راحت
ای کاش یکم معلما از شما یاد بگیرند
عالی بود، ممنونم، واقعا درس رو نفهمیده بودم سر کلاس های آنلاین، اینجا کامل متوجه شدم
ساده و قابل درک
عالیه همه چیز . امیدوارم همینطور عالی بمونه.
درودی فراوان خدمت همه دست اندرکاران کل تشکیلات فرادرس.
سایتی بسیار بسیار خوب با بار علمی بسیار بالا هستید.
آموزش هاتون عالیه.این وبلاگتونم که محشره.
عالی بود ممنونم
دمتون گرم خدا به زندگیتون برکت بده
کاش استادها اینقد. سخت نگن این درسها رو تا آدم زده نشه
سلام. من محمد مقدمی هستم کلاس هفتم. با اینکه ما تابع را درکلاس ات بالا میخوانیم اما با این توضیح همه چیز را فهمیدم
ممنون مفید مختصر کلی و دربرگینده تمام نکات اصلی دست شما درد نکنه
خیلی ممنونم از تدریس عالیتون. من هر مشکلی داشتم با سر زدن به وبسایت شما حل شده
سلام
خیلی ممنون از شما سایتتون خیلی عالیه خداروشکر با این مقاله تونستم مفهوم کلی توابع رو درک کنم
موفق باشید
سلام خسته نباشید بسیار عالی بود فقط کاش موزیک پشتشو نذاشته بودین خیلی تمرکز رو بهم میزنه.
مرسی عالی بود استاد
از افغانستان
سلام..
میشه لطفا بگویید: شما تدریس خصوصی هم دارید؟!
ممنون
شما فوق العاده اید 🙂
واقعا عالی و بی نقص بود.مشخصه که سر نوشتن این جزوه وقت و دقت زیادی گذاشته شده.واقعا مفید بود.اجرکم عندلله
ایا نمودار دایره یک تابع است؟
خیر چون اگر یک خط موازی محور y رسم کنیم نمودار را در 2 نقطه قطع میکند.یا اینکه به ازای یک ورودی نمی توان 2 خروجی داشت
سلام.
پیاده سازی زوج های مرتب در زبان هایی چون پایتون…
بسیار آموزنده میتواند واقع شود.
درودی فراوان خدمت همه دست اندرکاران کل تشکیلات فرادرس.
سایتی بسیار بسیار خوب با بار علمی بسیار بالا هستید.
آموزش هاتون عالیه.این وبلاگتونم که محشره.
فقط کمی بیشتر در زمینه هوش مصنوعی وقت بگذارید آموزش ها و مقالات زیادی رو در زمان های کوتاه از هم منتشر کنید.
سپاس فراوان.
بسیار عالی بود ..آرزوی موفقیت براتون دارم .درود به شرفتون
خیلی عالی بودممنون
بسیار عالی و مفید کاش معلم ها هم همینطوری درس میدادن
بسیار عالی بود
خیلی عالی بود ممنون که مطالب رو به طور ساده بیان کردید بهترین سایتی بود که تا حالا بازدید کردم
سلام دوستان یه سوال دارم.
در صورتی که y تابعی از x باشد،آیا × هم میتواند تابعی از y باشد؟
لطفاً هرکس از دوستان میدونه،جواب بده.
ممنون.
با سلام و درود فراوان خدمت استاد عزیز
خیلی ساده و تمام جزئیات پوشش قرار دادین ، ممنون بخاطر زحمتتون ??
مرسی واقعن عالی بود
خیلی ممنون از مطالب مفیدی که ذکر کرده بودید خیلی ساده ومفید بود توضیحات شما فقط اگه میشد یک کانال یا گروه تلگرامی هم میزدید خیلی عالی میشد
عالی بود واقعا ممنونم