تئوری پلاستیسیته جریان (Flow Plasticity Theory) — آشنایی با فرضیات پلاستیسیته

«پلاستیسیته جریان» (Flow plasticity)، یکی از تئوری‌های موجود در مکانیک جامدات است که به توصیف رفتار پلاستیک در مواد مختلف می‌پردازد. تئوری‌های پلاستیسیته جریان بر مبنای فرضیات قانون جریان شکل گرفته‌اند. این فرضیات به منظور تعیین تغییر شکل پلاستیک مواد مورد استفاده قرار می‌گیرند.

در تئوری‌های پلاستیسیته جریان، فرض می‌شود که امکان تجزیه کرنش کل در یک جسم را به صورت حاصل جمع یا ضرب یک بخش الاستیک و یک بخش پلاستیک وجود دارد. بخش الاستیک کرنش از طریق مدل‌های الاستیک خطی یا هایپرالاستیک قابل محاسبه است. اگرچه، برای تعیین بخش پلاستیک کرنش باید از یک قانون جریان و یک مدل سخت‌شوندگی استفاده کرد.

تئوری تغییر شکل کوچک

منحنی تنش-کرنش زیر را در نظر بگیرید. در این منحنی، نمونه‌ای از رفتار پلاستیک معمول مواد تحت فشار نمایش داده شده است. کرنش در این منحنی را می‌توان به دو بخش کرنش الاستیک قابل بازگشت (ε_e) و کرنش غیر الاستیک (ε_p) تجزیه کرد. تنش در نقطه تسلیم اولیه، σ₀ است.

فیلم آموزش مکانیک محیط پیوسته – جامع و کاربردی در فرادرس

کلیک کنید

برای موادی با خاصیت سخت‌شوندگی کرنش، با افزایش تغییر شکل پلاستیک، مقدار تنش تسلیم تا مقدار σ_y افزایش می‌یابد.

تئوری‌های پلاستیسیته معمول (برای تغییر شکل‌های کوچک با پلاستیسیته کامل یا پلاستیسیته سخت‌شوندگی)، بر اساس قواعد زیر توسعه یافته‌اند:

1. ماده دارای یک محدوده الاستیک خطی است (E).
2. ماده دارای یک حد الاستیک است (تنش σ₀ که در آن تغییر شکل پلاستیک شروع می‌شود).
3. پس از حد الاستیک، حالت تنش همیشه بر روی سطح تسلیم قرار خواهد داشت (σ=σ_y).
4. به حالتی که میزان افزایش تنش بیش‌تر از صفر باشد (dσ>0)، بارگذاری گفته می‌شود. در صورتی که بارگذاری باعث رسیدن حالت تنش به محدوده پلاستیک شود، افزایش کرنش پلاستیک همیشه بیشتر از صفر خواهد بود (dε_p>0).
5. به حالتی که افزایش میزان تنش کوچک‌تر از صفر باشد (dσ<0)، باربرداری گفته می‌شود. در حین باربرداری، ماده دارای رفتار الاستیک است و هیچ کرنش پلاستیکی درون آن رخ نمی‌دهد.
6. کرنش کل، یک ترکیب خطی از بخش‌های الاستیک و پلاستیک کرنش است (dε=dε_e+dε_p). بخش پلاستیک کرنش قابل بازگشت نیست؛ در صورتی که بخش الاستیک به طور کامل بازیابی می‌شود.
7. کار انجام شده در طی چرخه بارگذاری-باربرداری، مثبت یا صفر است (dσ*dε=dσ*(dε_e+dε_p)≥0). این قاعده با عنوان «اصل پایداری دراکر» (Drucker Stability Postulate) نیز شناخته می‌شود و احتمال وجود رفتار نرم شوندگی کرنش را حذف می‌کند.

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

قواعد بالا در فضای سه‌بعدی را می‌توان به صورت زیر تعریف کرد:

• الاستیسیته (قانون هوک): در محیط‌های الاستیک خطی، رابطه بین تنش و کرنش ماده به صورت زیر است:

D: ماتریس سختی با مقدار ثابت است.

• حد الاستیک (سطح تسلیم): حد الاستیک توسط سطح تسلیمی تعریف می‌شود که به کرنش پلاستیک وابسته نیست. رابطه کلی حد الاستیک به صورت است:

• محدوده پس از حد الاستیک: برای سنگ‌هایی که دارای خاصیت سخت‌شوندگی کرنش هستند، سطح تسلیم با افزایش کرنش پلاستیک توسعه می‌یابد و محل حد الاستیک تغیر می‌کند. توسعه سطح تسلیم دارای فرم کلی زیر است:

• بارگذاری: تعمیم شرط dσ>0 به فضای سه‌بعدی، مخصوصاً برای خاصیت پلاستیسیته سنگ‌ها کار ساده‌ای نیست. پلاستیسیته سنگ‌ها، علاوه بر تنش انحرافی به تنش میانگین نیز وابسته خواهد بود. با این وجود، در حین بارگذاری f≥0 و فرض می‌شود که جهت‌گیری کرنش پلاستیک با بردار نرمال سطح تسلیم (f/∂σ∂) یکسان است و dε_p≥dσ. یعنی:

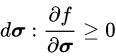
صفر بودن معادله بالا، حالت بارگذاری خنثی را نمایش می‌دهد. در این نوع بارگذاری، حالت تنش در امتداد سطح تسلیم حرکت می‌کند، بدون اینکه تغییری در کرنش پلاستیک ایجاد شود.

• باربرداری: مبحث باربرداری نیز مشابه بارگذاری است. در اینجا برای f<0، ماده در محدوده الاستیک قرار می‌گیرد و رابطه زیر برقرار است:

• تجزیه مؤلفه‌های کرنش: تجزیه مؤلفه‌های کرنش به حاصل جمع بخش‌های کرنش الاستیک و پلاستیک به صورت زیر نوشته می‌شود:

• اصل پایداری: اصل پایداری توسط رابطه زیر بیان می‌شود:

قانون جریان

در پلاستیسیته فلزات، فرض یکسان بودن جهات اصلی افزایش کرنش پلاستیک و تانسور تنش انحرافی توسط رابطه‌ای به نام «قانون جریان» (Flow Rule) نمایش داده می‌شود. تئوری‌های مرتبط با پلاستیسیته سنگ‌ها نیز از مفهوم مشابه ای بهره می‌گیرند. با این تفاوت که وابستگی سطح تسلیم به پارامتر فشار به یک «آسایش» (Relaxation) نیاز دارد. به جای این کار، معمولاً فرض می‌شود که افزایش کرنش پلاستیک و بردار نرمال سطح تسلیم وابسته به فشار، دارای جهت یکسانی هستند. به عبارت دیگر:

dλ>0، پارامتر سخت‌شوندگی را نشان می‌دهد. این فرم از قانون جریان با عنوان «قانون جریان همراه» (Associated Flow Rule) و فرض یکسان بود جهات با عنوان «شرط نرمال بودن» (Normality Condition) شناخته می‌شود. به تابع f، «تابع پتانسیل پلاستیک» (Plastic Potential Function) نیز می‌گویند.

قانون بالا برای تغییر شکل‌های کاملاً پلاستیک در شرایط dσ=0 و dε_p≥0 به سادگی تعمیم داده می‌شود. در این حالت، سطح تسلیم در هنگام افزایش تغییر شکل پلاستیک ثابت باقی می‌ماند. با توجه به قانون هوک، این موضوع بر صفر بودن میزان افزایش کرنش الاستیک (dε_e=0) دلالت خواهد داشت. بنابراین داریم:

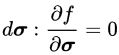
و

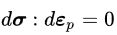
از این‌رو، بردار نرمال سطح تسلیم و تانسور کرنش پلاستیک بر تانسور تنش عمود هستند و در نتیجه باید جهت یکسانی داشته باشند. برای موادی با خاصیت کرنش سخت‌شوندگی، امکان گسترش سطح تسلیم با افزایش تنش وجود دارد. بر اساس فرضیه دوم پایداری دراکر، برای یک چرخه تنش بسیار کوچک، کرنش تغییرات پلاستیک مثبت خواهد بود. به عبارت دیگر:

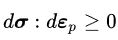
کمیت بالا در چرخه‌های کاملاً الاستیک برابر با صفر است. به منظور تصدیق اعتبار قانون جریان همراه می‌توان کار انجام شده در طی یک چرخه بارگذاری-باربرداری پلاستیک را مورد ارزیابی قرار داد.

شرط سازگاری

«شرط سازگاری پراگر» (Prager Consistency Condition) به منظور بستن مجموعه معادلات مشخصه و حذف پارامتر مجهول dλ از دستگاه معادلات مورد استفاده قرار می‌گیرد. با توجه به این شرط، به دلیل f(σ,ε_p)=0 در نقطه تسلیم df=0 خواهد بود و به این ترتیب داریم:

تئوری تغییر شکل بزرگ

تئوری‌های پلاستیسیته مرتبط با تغییر شکل بزرگ معمولاً با یکی از فرضیات زیر شروع می‌شوند:

• تجزیه تانسور نرخ تغییر شکل به حاصل جمع دو بخش الاستیک و پلاستیک
• تجزیه گرادیان تغییر شکل به حاصل ضرب دو بخش الاستیک و پلاستیک

فرض اول، کاربرد گسترده‌ای در شبیه‌سازی‌های عددی فلزات داشت اما فرض دوم به مرور جای آن را گرفت.

سینماتیک پلاستیسیته در رویکرد ضرب مؤلفه‌ها

مفهوم تجزیه ضربی گرادیان تغییر شکل به دو بخش الاستیک و پلاستیک، برای اولین بار توسط «بی. اِی بیلی» (B. A. Bilby) و «اکهارت کرونر» (Ekkehart Kröner) برای پلاستیسیته بلورها ارائه شد و توسط «اراسموس لی» (Erasmus Lee) برای پلاستیسیته محیط‌های پیوسته تعمیم یافت. در این تجزیه فرض می‌شود که گرادیان تغییر شکل کل (F) را می‌توان به صورت حاصل ضرب زیر نوشت:

F_e: بخش الاستیک تغییر شکل (برگشت‌پذیر)؛ F_p: بخش پلاستیک تغییر شکل (برگشت‌ناپذیر)

گرادیان سرعت به صورت تعیین می‌شود:

اندیس نقطه (.) بر روی پارامترها، بیانگر مشتق نسبت زمان است. معادله بالا را می‌توان به شکل زیر نوشت:

که در آن:

به کمیت L_p، گرادیان سرعت پلاستیک شناخته می‌گویند. این کمیت، در یک پیکربندی واسط (ناسازگار) عاری از تنش تعریف می‌شود. بخش متقارن (D_p) در کمیت L_p، نرخ پلاستیک تغییر شکل و بخش پادمتقارن (W_p) در این کمیت، چرخش پلاستیک نام دارد.

معمولاً در اکثر تعاریف پلاستیسیته محدود از بخش چرخش پلاستیک صرف نظر می‌شود.

رفتار الاستیک

رفتار الاستیک در حالت کرنش محدود معمولاً توسط مدل رفتاری هایپرالاستیک بیان می‌شود.

فیلم آموزش مکانیک محیط پیوسته – جامع و کاربردی در فرادرس

کلیک کنید

در این شرایط می‌توان کرنش الاستیک را با استفاده از یک تانسور تغییر شکل کوشی-گرین تعریف کرد:

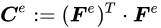
به این ترتیب، رابطه تانسور کرنش لگاریتمی به صورت زیر نوشته می‌شود:

یکی از معیارهای رایج در پلاستیسیته محدود، «تانسور تنش ماندل» (Mandel Stress Tensor) است که به صورت زیر تعریف می‌شود:

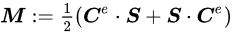
S، پارامتر تنش پیولا-کیرشهف مرتبه دوم است. رابطه زیر، یکی از مدل‌های هایپرالاستیک احتمالی با توجه به کرنش لگاریتمی را نشان می‌دهد:

W: تابع چگالی انرژی کرنشی؛ J: دترمینان گرادیان تغییر شکل؛ μ: مدول برشی؛ dev: بخش انحرافی تانسور

قانون جریان

در هنگام عدم حضور چرخش پلاستیک می‌توان از «نامساوی کلازیوس-دوهم» (Clausius-Duhem Inequality) برای تعیین قانون جریان کرنش محدود استفاده کرد:

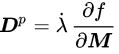
شرایط بارگذاری-باربرداری

شرایط بارگذاری-باربرداری را می‌توان به صورت برابر با «شرایط کاروش-کون-تاکر» (Karush-Kuhn-Tucker Conditions) نمایش داد:

شرط سازگاری

شرط سازگاری در تغییر شکل بزرگ همانند شرط سازگاری در کرنش کوچک است:

در صورتیکه به دنبال یادگیری مباحث مشابه هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های مهندسی عمران
• مجموعه آموزش‌های دروس مهندسی مکانیک
• آموزش مقاومت مصالح
• مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خصوصیات رفتاری مواد

^^