معادلات دیفرانسیل مرتبه اول — روش‌های حل به زبان ساده

در مطالب گذشته به تعریف معادلات دیفرانسیل و بررسی انواع آن پرداختیم. هم‌چنین در بخشی دیگر روش حل معادلات با مشتقات جزئی را توضیح دادیم. در این قسمت، قصد داریم تا در مورد روش‌های حل معادلات دیفرانسیل مرتبه اول صحبت کنیم. همان‌طور که قبلا نیز اشاره شد، یک معادله دیفرانسیل رابطه‌ای است که در آن یک تابع و مشتقاتش وجود داشته باشند.

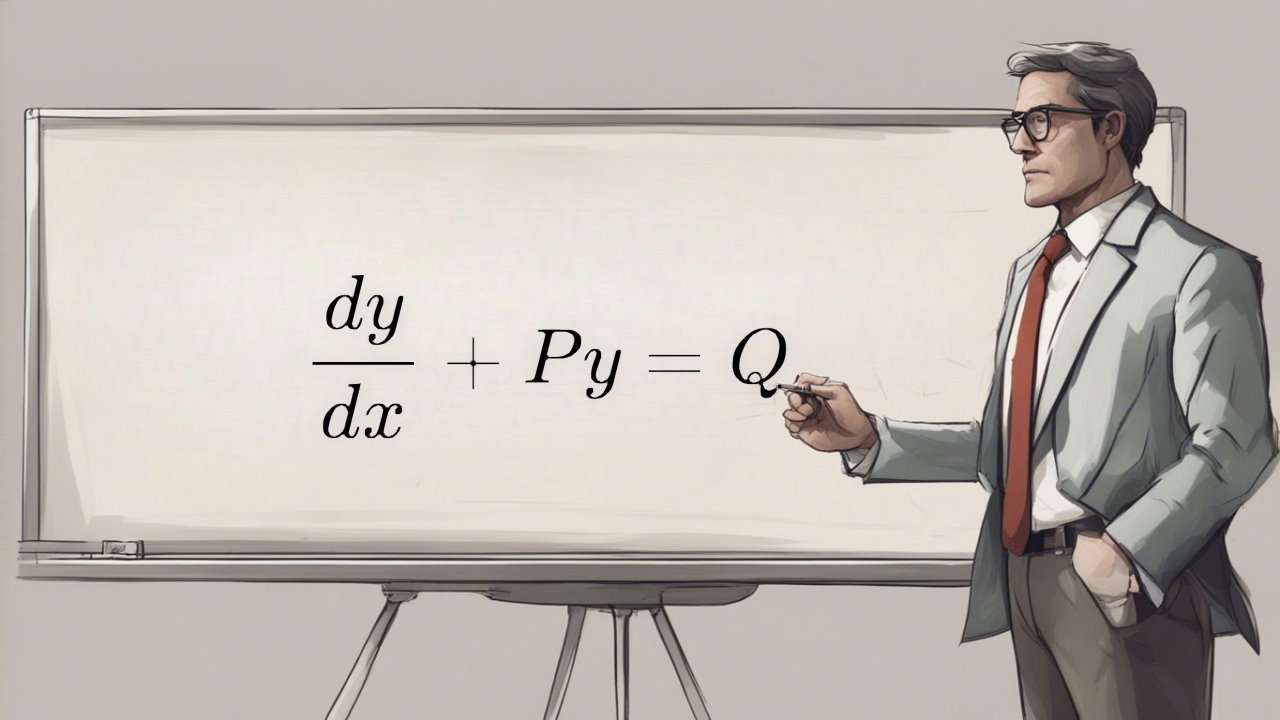
در ابتدا اجازه دهید تا با یکی از معروف‌ترین معادلات دیفرانسیل مرتبه اول، که همان قانون دوم نیوتن است، شروع کنیم. این قانون بیان می‌کند که اگر نیروی F به جسمی به جرم m وارد شود، جسم دارای شتاب a خواهد شد و رابطه زیر همواره برقرار خواهد بود:

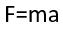
این معادله، یک رابطه دیفرانسیلی است، چرا‌ که می‌توان آن را به صورت زیر نوشت:

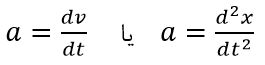
معادلاتی هم‌چون قانون دوم نیوتن را می‌توان با استفاده از روش جداسازی متغیر‌ها حل کرد.

معادلات جداپذیر

به معادلاتی که در آن متغیرها قابل جدا شدن باشند، معادلات جداپذیر گفته‌ می‌شود. فرمت کلی این نوع از معادلات به صورت زیر است:

فیلم آموزش معادلات دیفرانسیل به همراه حل سوالات آزمون کارشناسی ارشد در فرادرس

کلیک کنید

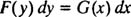
توجه داشته باشید، هنگامی که معادله‌ای به فرمت بالا نوشته شود، می‌توان با انتگرال‌گیری از طرفین آن، تابع y را نسبت به متغیر x پیدا کرد. بنابراین جواب نهایی معادله‌ای که جداپذیر است، به صورت زیر خواهد بود:

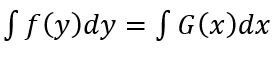
روش جداسازی متغیرها، به شکلی خلاصه بیان می‌کند که: متغیرها را جدا کن و انتگرال بگیر. در ادامه به بررسی چند مثال از این روش خواهیم پرداخت.

مثال 1:

معادله زیر را حل کنید.

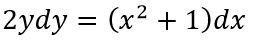
پیشنهاد می‌کنیم قبل از مطالعه، در مورد پاسخ این سوال فکر کنید. همان‌طور که دیده می‌شود این معادله به صورت فرمتی بیان شده که نشان دهنده یک معادله جدا‌ پذیر است.

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

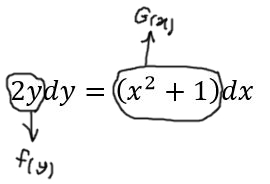
کاملا بدیهی است که با انتگرال‌گیری از طرفین، می‌توان به پاسخ این معادله دست یافت. بنابراین خواهیم داشت:

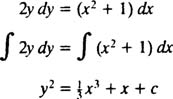
همان‌طور که مشاهده می‌کنید، این روش بسیار به‌صرفه و آسان است. توصیه می‌شود قبل از حل معادلات دیفرانسیل مرتبه اول، در مورد جداپذیر بودن آن‌ها بررسی‌های لازم انجام شود.

مثال 2:

در این‌جا قصد داریم معادله‌ای سخت‌تر را مورد بررسی قرار دهیم. رابطه زیر را در نظر بگیرید:

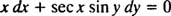
به منظور حل معادله‌ای که به صورت جداسازی متغیرها قابل حل است، در ابتدا بایستی ضرایب dx در یک سمت و ضرایب dy در سمت دیگر قرار گیرد. بنابراین داریم:

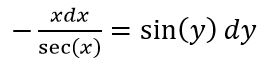
همان‌طور که می‌بینید، xها به طور کامل در یک سمت و yها در سمت دیگر قرار گرفته‌اند. انتگرال سمت راست معادله برابر است با:

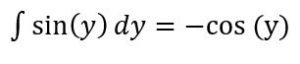
به همین روش انتگرال سمت چپ به شکل زیر محاسبه می‌شود:

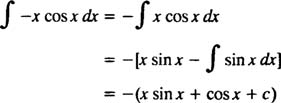
بنابراین پاسخ معادله دیفرانسیل مفروض به صورت زیر خواهد بود:

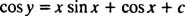
دقت شود که به ازای هر ثابت c، پاسخ بدست آمده در معادله صدق خواهد کرد؛ اما در معادلاتی که مقدار اولیه یا شرایط مرزی در آن تعریف شده باشند، می‌توان این ثابت‌ها را بدست آورد. به مثالی که در ادامه آمده‌ است توجه فرمایید.

فیلم آموزش ریاضیات مهندسی پیشرفته در فرادرس

کلیک کنید

مثال 3:

معادله زیر را به روش جداسازی متغیرها حل کنید.

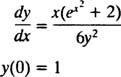
همان‌طور که در معادله می‌بینید، یک مقدار اولیه در صفر تعریف شده است. این عدد به ما کمک می‌کند تا ثابت‌های ظاهر شده در معادله، پیدا شوند. با مرتب کردن معادله مفروض، می‌توان نوشت:

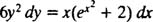
بنابراین توابع y در یک سمت و توابع x در سمت دیگر قرار گرفتند. با انتگرال‌گیری داریم:

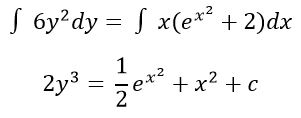
پارامتر c با استفاده از مقدار اولیه تعریف شده در x=0 به شکل زیر محاسبه می‌گردد:

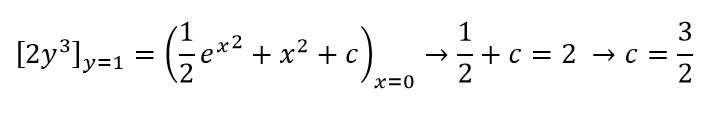
در نتیجه پاسخ نهایی به صورت زیر خواهد بود:

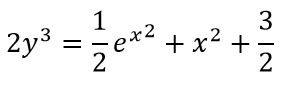
در مواردی ممکن است با دو و یا چند بار انتگرال‌گیری به پاسخ معادله دست یافت. در این مثال قصد داریم به حل معادله‌ای بپردازیم که در ابتدای این مطلب به آن اشاره کردیم.

مثال 4:

قانون دوم نیوتن را به صورت دیفرانسیلی در نظر بگیرید. منظور از دیفرانسیلی، فرمت زیر است:

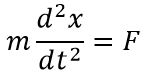
این معادله دارای مشتق مرتبه دوم است؛ بنابراین در پاسخ آن دو ثابت ظاهر خواهد شد. با دوبار انتگرال‌گیری می‌توان به جواب این معادله دست یافت:

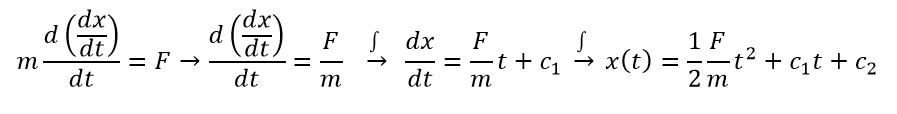
نتیجه‌گیری

همان‌طور که مشاهده می‌کنید، روش جداسازی متغیرها، گزینه مناسبی به منظور حل معادلات دیفرانسیل محسوب می‌شود. اما بایستی دقت کرد که در بسیاری از معادلات مطرح شده نمی‌توان از این روش استفاده کرد، چرا که معمولاً در آن‌ها امکان انجام این جداسازی وجود ندارد. در ادامه نوع خاصی از معادلات دیفرانسیل را معرفی خواهیم کرد که در آن‌ها با استفاده از یک تغییر متغیر مشخص می‌توان عمل جداسازی را انجام داد.

معادلات همگن

حال که به بررسی معادلات جداپذیر پرداختیم، وقت آن رسیده که در مورد «معادلات همگن» (Homogeneous Equations)، صحبت کنیم. یک معادله همگن به معادله‌ای گفته می‌شود که در آن ضرایب dx و dy همگن باشند. به منظور توضیح بیشتر، معادله زیر را در نظر بگیرید:

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

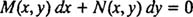
همگن بودن معادله مفروض به این شرط است که دو تابع M و N، همگن باشند. شاید این سوال برایتان پیش بیاید که تابع همگن چه تابعی است؟ تابعی همگن است که شرط زیر در آن صدق کند:

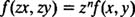
به عنوان مثال رابطه زیر را در نظر بگیرید:

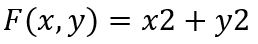
حال به منظور بررسی همگن بودن این معادله، به جای x و y، در آن zx و zy قرار می‌دهیم. بنابراین داریم:

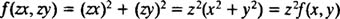
همان‌طور که مشاهده می‌کنید، این تابع همگن است. حال، تابع زیر را در نظر بگیرید:

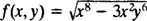
مشابه مثال قبلی با قرار دادن zx و zy در آن داریم:

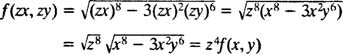
این معادله نیز همانند رابطه اول، همگن است. در این دو مثال توابع مورد بررسی، همگن بودند. به منظور بررسی یک تابع ناهمگن، معادله زیر را در نظر بگیرید:

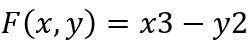
همانند مثال‌های قبلی تابع (F(zx,zy را بدست می‌آوریم. بنابراین:

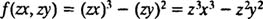
با توجه به معادله بالا بدیهی است که این تابع به فرمت مد‌نظر در نخواهد آمد. بنابراین در نظر داشته باشید که هرگاه ضرایب dx و dy در معادلات دیفرانسیل مرتبه اول همگن باشند، آن معادلات را همگن در نظر می‌گیریم.

به منظور حل معادلات دیفرانسیل مرتبه اول همگن، از تغییر متغیر y=ux استفاده کنید. آن‌گاه معادله به دست آمده را بر حسب u و x مرتب کنید، خواهید دید که معادله بدست آمده با استفاده از روش جداسازی متغیرها قابل حل خواهد بود.

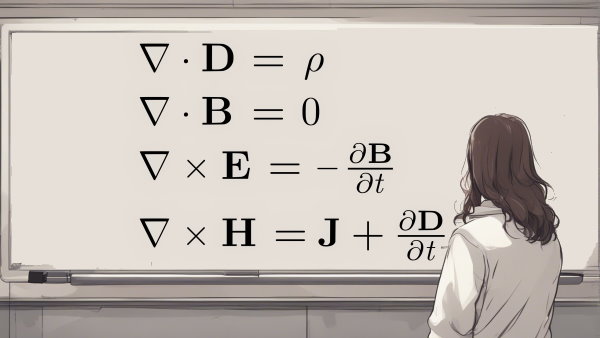
تا اینجا با معادلات همگن و جداپذیر آشنا شدیم. برای آشنایی با حل انواع معادلات دیفرانسیل می‌توانید به مجموعه آموزش معادلات دیفرانسیل – درس، تمرین، حل مثال و تست فرادرس مراجعه کنید.

مثال 1:

معادله دیفرانسیل زیر را حل کنید.

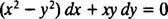
همان طور که می‌بینید در این معادله M و N به ترتیب برابر هستند با:

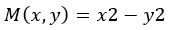
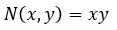
N و M همگن هستند، بنابراین معادله شکل گرفته از آن‌ها نیز این ویژگی را خواهد داشت. در مرحله بعد با استفاده از تغییر متغیر y=vx، می‌توان معادله اصلی را به شکل جداپذیر بیان کرد. با استفاده از این تغییر و جایگذاری آن در معادله اصلی خواهیم داشت:

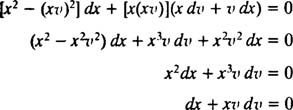
این معادله نیز با استفاده از روش جداسازی متغیرها و به شکل زیر، قابل حل است.

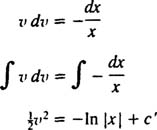
دقت شود که پاسخ اولیه بر حسب v و x و به صورت بالا خواهد شد؛ همچنین با جایگزین کردن y/x به جای v، می‌توان پاسخ نهایی را بر حسب y و x به دست آورد. در نتیجه خواهیم داشت:

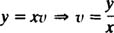
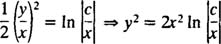
مثال 2:

لطفا مثال زیر را مد نظر قرار دهید چرا‌ که چندین نکته در آن نهفته است:

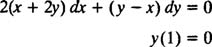
همان‌طور که دیده می‌شود، ضرایب dx و dy در این معادله، همگن هستند. بنابراین این معادله نیز از نوع همگن خواهد بود. در نتیجه می‌توانیم از تغییر متغیر y=vx، استفاده می‌کنیم. با استفاده از این تغییر متغیر و مرتب کردن معادله بر حسب x و v، می‌توان از روش جداسازی متغیر‌ها استفاده کرد. در نتیجه می‌توان گفت:

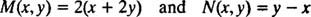
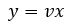
با فرضیات صورت گرفته و جایگذاری مقادیر، در معادله اصلی خواهیم داشت:

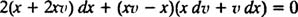
پس از مرتب کردن این معادله، به عبارت زیر می‌رسیم:

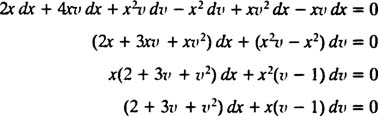
همان‌طور که می‌بینید این معادله، با روش جداسازی متغیرها قابل حل است. بنابراین می‌توان گفت:

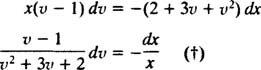
به منظور محاسبه انتگرال سمت چپ معادله، بایستی کسرها را به شکل زیر گویا کرد:

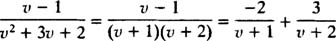
در نتیجه:

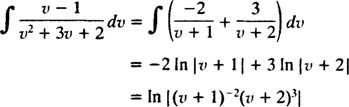
از طرفی با انتگرال‌گیری از سمت راست معادله، به عبارت زیر خواهیم رسید:

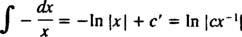
نهایتا با برابر قرار دادن انتگرال سمت راست و چپ می‌توان گفت:

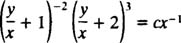
بنابراین دقت کنید، چرا که در بعضی از مسائل کسرهایی وجود خواهند داشت که ممکن است مخرج آن‌ها از درجه 2 یا 3 یا بیشتر باشند؛ در چنین مواردی اولین روشی که بایستی مد نظر قرار گیرد، گویا کردن کسرها است. در آینده بیشتر در مورد حل مسائلی از مراتب بالاتر صحبت خواهیم کرد.