الگوریتم کرم شب تاب – از صفر تا صد

«الگوریتم‌های الهام گرفته شده از طبیعت» (Nature-Inspired Algorithms)، در زمره قدرتمندترین الگوریتم‌های «بهینه‌سازی» (Optimization) قرار دارند. در این مطلب، یک الگوریتم بهینه‌سازی به نام «الگوریتم کرم شب تاب» (FA | Firefly Algorithm) مورد بررسی قرار می‌گیرد. ویژگی مهم الگوریتم کرم شب تاب، که آن را از برخی از الگوریتم‌های بهینه‌سازی مشابه متمایز می‌کند، عملکرد بسیار خوب آن در جستجوی جواب‌های بهینه مرتبط با مسائل و توابع «چندمُدی» (Multimodality) است. چنین ویژگی مهمی در الگوریتم کرم شب تاب سبب شده است تا این الگوریتم، به انتخاب ایده‌آلی برای کاربردهای بهینه‌سازی چندمُدی تبدیل شود.

در این مطلب، ابتدا مکانیزم‌ها و مؤلفه‌های الگوریتم کرم شب تاب (جهت «همگرایی» (Convergence) به جواب «بهینه سراسری» (Optimal Solution))، با جزئیات کامل و دقیق مورد بررسی قرار می‌گیرند. سپس، الگوریتم کرم شب تاب با دیگر الگوریتم‌های «فرا اکتشافی» (Meta-Heuristics) نظیر «بهینه‌سازی ازدحام ذرات» (Particle Swarm Optimization | PSO) مقایسه خواهد شد. شبیه‌سازی‌ها و نتایج حاصل نشان می‌دهد که الگوریتم کرم شب تاب عملکرد به مراتب بهتری نسبت به روش‌های «بهینه‌سازی ازدحامی» (Swarm Optimization) از خود نشان می‌دهد. در نهایت، کاربردهای الگوریتم کرم شب تاب در حوزه‌های مختلف و جهت‌گیری پژوهشی آن در آینده مورد بحث و بررسی قرار می‌گیرد.

مقدمه

«بهینه‌سازی» (Optimization)، به فرآیند تغییر و دستکاری ورودی‌ها، عملیات ریاضی یا خصوصیات یک دستگاه گفته می‌شود که با هدف رسیدن به یک خروجی یا جواب بهینه انجام می‌شود. ورودی‌ فرآیند بهینه‌سازی، متغیرهای مسأله‌ای هستند که قرار است به وسیله یکی از الگوریتم‌های خانواده روش‌های «بهینه‌سازی عددی» (Numerical Optimization) پردازش و جواب‌های بهینه آن مشخص شود. خروجی فرآیند بهینه‌سازی، «برازندگی» (Fitness) نامیده می‌شود؛ به فرآیند یا تابعی که قرار است توسط الگوریتم‌های بهینه‌سازی پردازش شود، «تابع هدف» (Objective Function) گفته می‌شود.

الگوریتم‌های بهینه‌سازی عددی مبتنی بر فرایندهای طبیعی، به یکی از مهم‌ترین زیر شاخه‌های حوزه «محاسبات تکاملی» (Evolutionary Computation) تبدیل شده‌اند. این دسته از روش‌های محاسباتی، الگوریتم‌هایی هستند که برای حل مسائل مختلف و بهینه‌سازی عددی آن‌ها پیاده‌سازی شده‌اند.

یکی از مهم‌ترین نمونه‌های چنین الگوریتم‌هایی، الگوریتم ژنتیک (و دیگر الگوریتم‌های مبتنی بر این روش محاسباتی) است که از مکانیزم‌های الهام گرفته شده از تکامل زیستی (نظیر «جهش» (Mutation)، «ترکیب» (Recombination)، «تولید مثل» (Reproduction)، «انتخاب طبیعی» (Natural Selection) و «بقای بهترین‌ها» (Survival of Fittest)) برای تولید جواب‌های کاندید، جهت حل یک مسأله بهینه‌سازی، استفاده می‌کنند. به این مکانیزم‌ها، عملگرهای تکاملی نیز گفته می‌شود.

جواب‌های کاندید، نقش نمونه‌ها را در جمعیت ایفا می‌کنند. «تابع هزینه» (Cost Function) نیز برازندگی محیطی را که جواب کاندید در آن قرار دارد (یک جواب کاندید برای مسأله بهینه‌سازی) مشخص می‌کند. الگوریتم‌هایی نظیر الگوریتم ژنتیک، الگوریتم کلونی مورچگان، الگوریتم کرم شب تاب، الگوریتم بهینه‌سازی فاخته و سایر موارد از جمله مهم‌ترین الگوریتم‌های تکاملی هستند.

در چند سال اخیر، الگوریتم‌های الهام گرفته شده از فرایندهای زیستی (Biologically-inspired Algorithm) به یکی از قدرتمندترین تکنیک‌ها و ابزارهای «بهینه‌سازی عددی» (Numerical Optimization) تبدیل شده‌اند؛ به ویژه، در حل مسائل با درجه پیچیدگی NP-Hard، نظیر «مسأله فروشنده دوره‌گرد» (Travelling Salesman Problem)، بسیار قدرتمند ظاهر شده‌اند و در مدت زمان بسیار معقولی به جواب بهینه سراسری همگرا می‌شوند.

در این میان، الگوریتم‌های مبتنی بر «هوش ازدحامی» (Swarm Intelligence) و «الگوریتم‌های فرا اکتشافی چند عامله» (Multi-Agent Meta-Heuristic Algorithm) جایگاه ویژه‌ای در حوزه بهینه‌سازی عددی دارند و به عنوان یکی از داغ‌ترین سوژه‌های تحقیقاتی در این حوزه قلمداد می‌شوند. الگوریتم‌هایی نظیر بهینه‌سازی ازدحام ذرات (PSO)، که زیر مجموعه الگوریتم‌های فرا اکتشافی چند عامله و مبتنی بر هوش ازدحامی است، جزء پیشرفته‌ترین الگوریتم‌های توسعه داده شده در بهینه‌سازی و دیگر کاربردهای مشابه هستند.

الگوریتم بهینه‌سازی ازدحام ذرات (PSO)، در سال 1995، توسط دو دانشمند به نام‌های کندی (Kennedy) و ابرهارت (Eberhart) ابداع شده است. الگوریتم بهینه‌سازی ازدحام ذرات بر پایه «رفتارهای ازدحامی» (Swarm Behaviors) گونه خاصی از موجودات زنده نظیر رفتارهای اجتماعی پرواز پرندگان برای یافتن غذا یا حرکت گروهی و در جهت یکسان ماهی‌ها الهام گرفته شده است. همانطور که پیش از این نیز اشاره شد، به چنین رفتاری در موجودات زنده، که الهام بخش توسعه برخی از الگوریتم‌های بهینه‌سازی معروف نیز هستند، هوش ازدحامی (Swarm Intelligence) گفته می‌شود.

با اینکه الگوریتم بهینه‌سازی ازدحام ذرات وجه شباهت‌های زیادی با «الگوریتم ژنتیک» (Genetic Algorithm) دارد، ولی از لحاظ ساختاری، به مراتب ساده‌تر از این الگوریتم است؛ دلیل این امر این است که در الگوریتم بهینه‌سازی ازدحام ذرات، از «عملگرهای تکاملی» (Evolution Operators) نظیر «ترکیب یا آمیزش» (Crossover) و «جهش» (Mutation) استفاده نمی‌شود. در این الگوریتم، از مکانیزم‌های تکاملی نظیر «تصادفی بودن» (Randomness) اعداد حقیقی و «ارتباطات سراسری» (Global Communications) میان ذرات ازدحامی، جهت رسیدن به تکامل و دست‌یابی به جواب بهینه سراسری استفاده می‌‎شود.

از سوی دیگر، از آنجایی که تمامی نمایش‌های تولید شده از جمعیت، «کدبندی‌های» (ٍEncodings) متناظر از موجودیت‌های «جمعیت» (Population) و مکانیزم‌های تکاملی استفاده شده برای همگرایی به جواب‌های بهینه (در الگوریتم بهینه‌سازی ذرات)، مبتنی بر عملیاتی هستند که عمدتا روی «اعداد حقیقی» (Real Numbers) انجام می‌شوند، پیاده‌سازی آن نیز راحت‌تر از الگوریتم ژنتیک خواهد بود.

در این مطلب، هدف ارائه مکانیزم‌ها و مؤلفه‌های الگوریتم کرم شب تاب جهت حل مسائل بهینه‌سازی عددی و جزئیات مرتبط با آن‌ها است. همچنین در این مطلب، مطالعه مقایسه‌ای از الگوریتم کرم شب تاب با الگوریتم‌هایی نظیر بهینه‌سازی ازدحام ذرات و دیگر الگوریتم‌های بهینه‌سازی مشابه ارائه خواهد شد. بنابراین، ساختار مطلب پیش رو به این صورت است که ابتدا الگوریتم بهینه‌سازی ازدحام ذرات و جزئیات آن معرفی خواهد شد. سپس، جزئیات مرتبط با مکانیزم‌ها و مؤلفه‌های الگوریتم کرم شب تاب ارائه خواهد شد. در مرحله آخر نیز، عملکرد الگوریتم کرم شب تاب با دیگر الگوریتم‌های بهینه‌سازی نظیر الگوریتم بهینه‌سازی ازدحام ذرات بررسی خواهد شد.

نتایج مقایسه عملکرد الگوریتم کرم شب تاب با دیگر الگوریتم‌های بهینه‌سازی نشان می‌دهد که این الگوریتم، به شکل بهتر و کارآمدتری می‌تواند به بهینه سراسری توابع چندمُدی همگرا شود؛ در نتیجه، الگوریتم کرم شب تاب انتخاب مناسب‌تری برای حل مسائل بهینه‌سازی چندمُدی و همگرایی به بهینه‌های سراسری این دسته از مسائل خواهد بود. بنابراین با در نظر گرفتن حالت ذکر شده، می‌توان نتیجه گرفت که الگوریتم بهینه‌سازی ازدحام ذرات، حالت خاصی از الگوریتم کرم شب تاب محسوب می‌شود (در ادامه، به این موضوع بیشتر پرداخته خواهد شد).

الگوریتم بهینه‌سازی ازدحام ذرات (PSO)

پیش از اینکه الگوریتم کرم شب تاب و ساختار آن مورد بررسی قرار بگیرد، الگوریتم بهینه‌سازی ازدحام ذرات به طور مختصر معرفی خواهد شد. مطالعه ویژگی‌های الگوریتم بهینه‌سازی ازدحام ذرات به خوانندگان و مخاطبان این مطلب کمک می‌کند تا شباهت‌‌ها و تفاوت‌های میان این دو الگوریتم و همچنین، نقاط ضعف و قوت آن‌ها در حل مسائل مختلف بهینه‌سازی را به شکل بهتری درک کنند.

الگوریتم استاندارد بهینه‌سازی ازدحام ذرات

در الگوریتم بهینه‌سازی ازدحام ذرات (PSO)، به هر کدام از «عوامل» (Agents) موجود در جمعیت «ذره» (Particles) گفته می‌شود. در الگوریتم PSO، به موازات شکل‌گیری شبه تصادفی «مسیرهای تکه‌ای» (Piecewise Paths) متناظر با هر یک از عوامل توسط «بردارهای مکانی» (Positional Vectors)، فضای جستجوی «توابع هدف» (Objective Functions) از طریق «تنظیم» (Adjust) کردن «مسیرهای» (Trajectories) هر کدام از عوامل موجود در جمعیت (ذرات) جستجو می‌شود (برای یافتن جواب بهینه یا ناحیه در بر گیرنده جواب بهینه).

در حال حاضر بیش از 20 نسخه مختلف از الگوریتم بهینه‌سازی ازدحام ذرات معرفی شده است. در این بخش، ساده‌ترین و البته محبوب‌ترین نسخه الگوریتم بهینه‌سازی ازدحام ذرات (الگوریتم استاندارد بهینه‌سازی ازدحام ذرات) معرفی خواهد شد.

حرکت ذرات در فضای جستجو به دو «مؤلفه» (Components) اساسی بستگی دارد: یک مؤلفه تصادفی (Stochastic) و یک مؤلفه قطعی (Deterministic). هر کدام از ذرات موجود در جمعیت، علاوه بر اینکه تمایل دارد به صورت تصادفی در فضای مسأله حرکت کند، به طور همزمان، به سمت نقطه‌ای که بهینه سراسری یا پارامتر $$g \star$$ در آن قرار گرفته است، جذب می‌شود. به عبارت دیگر، هر کدام از ذرات موجود در جمعیت، به سمت مکان بهترین نقطه‌ای (در فضای مسأله) که ذرات تا کنون در آن قرار گرفته‌اند (بهترین نقطه، بر اساس تاریخچه حرکت ذرات در محیط سنجیده می‌شود) یا پارامتر $$x _ i ^ *$$، جذب می‌شوند.

زمانی که یکی از ذرات موجود در جمعیت (ذره $$i$$)، مکانی را در فضای جستجو پیدا کند که از دیگر مکان‌های جستجو شده در این فضا بهتر باشد، مکان جدید یافته شده به عنوان بهترین نقطه‌ای (در فضای مسأله) که ذره $$i$$ تا کنون در آن قرار گرفته است، به‌روزرسانی می‌شود. این مکان جدید در فضای مسأله، به عنوان بهترین جواب ممکن برای تمامی $$n$$ ذره موجود در جمعیت شناخته خواهد شد.

هدف نهایی الگوریتم بهینه‌سازی ازدحام ذرات این است که جواب بهینه سراسری را از میان مجموعه بهترین جواب‌های ممکن یافت شده (توسط ذرات) مشخص کند. فرایند یافتن بهترین جواب‌های ممکن (توسط ذرات) تا زمانی ادامه پیدا می‌کند که پس از تعداد تکرارهای مشخصی، دیگر بهبود قابل ملاحظه‌ای در بهترین جواب ممکن ایجاد نشود. بهترین جواب موجود در مجموعه جواب‌های بهینه یافت شده، به عنوان جواب بهینه سراسری مسأله مشخص می‌شود.

جهت نمایش حرکت ذرات در فضای مسأله، از $$x _ i ^ *$$ برای مشخص کردن بهترین نقطه (جواب) یافت شده توسط ذره $$i$$ و از رابطه زیر:

$$g \star \approx min \; or \; max \left \{ f ( x _ { i } ) \right \} ( i = 1 , 2 , . . . ., n )$$

برای مشخص کردن جواب بهینه سراسری (بهترین جواب موجود در مجموعه جواب‌های بهینه یافت شده توسط ذرات) استفاده می‌شود.

با فرض اینکه $$x _ { i }$$ و $$v _ { i }$$ به ترتیب بردار مکان و «سرعت» (Velocity) ذره $$i$$ باشند، بردار سرعت جدید از طریق رابطه زیر به دست می‌آید:

$$v _ i ^ { t + 1 } = v _ i ^ { t } + \alpha \epsilon _ { 1 } \circledcirc ( g \star - x _ i ^ { t } ) + \beta \epsilon _ { 2 } \circledcirc ( x _ i ^ { * } - x _ i ^ { t } )$$

در این رابطه، $$\epsilon _ { 2 }$$ و $$\epsilon _ { 1 }$$ دو بردار تصادفی هستند و هر کدام از عناصر این بردارها، مقداری تصادفی بین 0 و 1 به خود می‌گیرند. «ضرب آدامار» (Hadamard Product) دو ماتریس $$u\circledcirc v$$ در قالب «ضرب عنصر به عنصر» (Entry-wise Product) تعریف و به شکل زیر نمایش داده می‌شود:

$$| u \circledcirc v | _ { i j } = u _ { i j } v _ { i j }$$

پارامترهای $$\alpha$$ و $$\beta$$، «پارامترهای یادگیری» (Learning Parameters) یا «ثابت‌های شتاب» (Acceleration Constants) نام دارند. این دو پارامتر  معمولا به شکل $$\alpha \approx \beta \approx 2$$ مقداردهی می‌شوند. مقادیر ابتدایی پارامتر $$X _ i ^ { t = 0 }$$، با استفاده از حدهای بالا و پایین $$a = min ( x _ { i } ) , \; b = max ( x _ { j } )$$ مشخص می‌شود. همچنین، مقدار ابتدایی پارامتر $$V _ i ^ { t = 0 }$$  برابر با صفر در نظر گرفته می‌شود ($$V _ i ^ { t = 0 } = 0$$).

با توجه به روابط فوق و مقادیر پارامترها، مکان جدید ذره $$i$$ در فضای جستجو، از طریق رابطه زیر مشخص می‌شود:

$$X _ i ^ { t + 1 } = X _ i ^ { t } + V _ i ^ { t + 1 }$$

اگرچه پارامتر $$V _ i$$ می‌تواند هر مقداری به خود بگیرد، ولی معمولا مقدار این پارامتر از بازه $$\left [ 0 , V _ { max } \right ]$$ انتخاب می‌شود.

تاکنون نسخه‌های مختلفی از الگوریتم بهینه‌سازی ازدحام ذرات معرفی شده است. مهم‌ترین بهبودی که در نسخه‌های مختلف الگوریتم بهینه‌سازی ازدحام ذرات و در مؤلفه‌های آن ایجاد شده است، استفاده از «تابع اینرسی» (Inertia Function) به فرم $$\theta ( t )$$ است. در نسخه‌هایی از الگوریتم بهینه‌سازی ازدحام ذرات که از تابع اینرسی استفاده می‌کند، به جای پارامتر $$V _ i ^ { t }$$ از عبارت $$\theta ( t ) V _ i ^ { t }$$ استفاده می‌شود؛ در این عبارت، پارامتر $$\theta$$ مقادیری بین 0 و 1 به خود می‌گیرد.

در ساده‌ترن حالت، تابع اینرسی را می‌توان به عنوان یک ثابت در الگوریتم بهینه‌سازی ازدحام ذرات در نظر گرفت که مقادیری به شکل $$\theta \approx 0.5 \approx 0.9$$ به خود می‌گیرد. اضافه کردن تابع اینرسی (به شکل یک پارامتر ثابت) را می‌توان به عنوان یک «جرم مجازی» (Virtual Mass) تصور کرد که حرکت ذرات در فضای جستجوی مسأله را پایدار می‌کند؛ در نتیجه، انتظار می‌رود که در چنین حالتی، الگوریتم بهینه‌سازی ازدحام ذرات با سرعت بیشتری به جواب بهینه سراسری همگرا شود (یا ذرات موجود در جمعیت، با سرعت بیشتری به سمت ناحیه دربرگیرنده جواب بهینه سراسری همگرا شوند).

الگوریتم کرم شب تاب

در این بخش، مکانیزم‌ها و مؤلفه‌های الگوریتم کرم شب تاب (جهت «همگرایی» (Convergence) به جواب «بهینه سراسری» (Optimal Solution))، با جزئیات کامل و دقیق مورد بررسی قرار می‌گیرد.

رفتار کرم‌های شب تاب

یکی از صحنه‌های جذاب و زیبایی که گردشگران و ساکنین مناطق استوایی یا معتدل، در آسمان شب‌های فصل تابستان، با آن موجه می‌شوند، «نور چشمک‌زن» (Flashing Light) کرم‌های شب تاب است. تا به امروز، چیزی حدود 2 هزار گونه متفاوت از کرم‌های شب تاب در دنیا به ثبت رسیده است و بیشتر آن‌ها، نورهای چشمک‌زن «متناوب» (Rhythmic) و کوتاهی را تولید می‌کنند. معمولا، هر یک از گونه‌های کرم شب تاب، الگوهای نور چشمک‌زن یکتا و منحصر به فردی تولید می‌کنند.

نور چشمک‌زنی که توسط کرم‌های شب تاب ساطع می‌شود، در نتیجه فرایند زیستی به نام «لومینسانس زیستی یا فسفر افکنی» (Bioluminescence) ایجاد می‌شود که سبب ایجاد پدیده شب تابی در کرم‌های شب تاب می‌شود. تاکنون، بحث‌ها و مطالعات زیادی در مورد کارکرد این نورهای چشمک‌زن انجام شده است ولی دانشمندان نتوانستند به نظریه واحدی در رابطه با کارکرد واقعی آن‌ها دست پیدا کنند. با این حال، دو کارکرد بنیادی فرایند لومینسانس زیستی و شب تابی حاصل از آن، عبارتند از:

• جذب کردن جنس مخالف برای جفت‌گیری و آمیزش (کارکرد ارتباطی (Communication) فرایند لومینسانس زیستی)
• جذب کردن طعمه‌های محتمل به سمت خود

علاوه بر این، محققان دریافته‌اند که کرم‌های شب تاب از نورهای چشمک‌زن به عنوان یک مکانیزم محافظتی جهت ارسال هشدار به دیگر کرم‌های شب تاب موجود در محیط استفاده می‌کنند. ریتم یا تناوب نور چشمک‌زن، نرخ چشمک زدن نور و مدت زمان چشمک زدن نور توسط کرم‌های شب تاب، بخش‌های مختلف سیستم ارتباطی میان کرم‌ها ( جهت جفت‌گیری با جنس مخالف یا هشدار به کرم‌های شب تاب موجود در محیط در مورد خطرات محتمل) را شکل می‌دهد.

به عنوان نمونه، در هنگام جفت‌گیری کرم‌های شب تاب، کرم ماده (از یک گونه خاص) به الگوی چشمک زن منحصر به فرد کرم‌های مذکر (از همان گون خاص) واکنش نشان می‌دهد. همچنین، در برخی از گونه‌های کرم شب تاب نظیر «فوتوریس» (Photuris)، کرم ماده این قابلیت را دارد که الگوی چشمک زن منحصر به فرد دیگر گونه‌ها (جهت جفت‌گیری) را تقلید کند. با چنین کاری، کرم شب تاب ماده می‌تواند کرم‌های مذکر گونه‌های دیگر را، که برای جفت‌گیری به سمت کرم ماده حرکت کرده‌اند، به دام بیاندازد و بخورد.

یکی از نکاتی که باید در مورد الگوی چشمک زن نوری کرم‌های شب تاب به خاطر داشته باشید این است که «شدت نور» (Light Intensity) در یک فاصله مشخص، $$r$$، از «منبع نور» (Light Source)، از «قانون مربع معکوس» (Inverse Square Law) تبعیت می‌کند. به عبارت دیگر، شدت نور، $$I$$، با افزایش فاصله، $$r$$، مطابق با رابطه $$I \propto \frac { 1 } { r ^ { 2 } }$$ کاهش پیدا می‌کند. علاوه بر این، «هوا» (Air) نور را جذب می‌کند که به نوبه خود سبب می‌شود تا شدت نور، با افزایش فاصله، ضعیف و ضعیف‌تر شود.

ترکیب این دو عامل مهم سبب می‌شود تا کرم‌های شب تاب، تنها از فاصله مشخصی قابل مشاهده باشند؛ معمولا، در تاریکی شب، نور چشمک‌زن کرم‌های شب‌تاب از فاصله چند صد متری قابل رؤیت است که برای مشاهده شدن توسط دیگر کرم‌ها و برقراری ارتباط با آن‌ها کفایت می‌کند.

نور چشمک‌زن تولید شده توسط کرم‌های شب تاب را می‌توان به گونه‌ای فرمول‌بندی (Formulate) کرد که متناظر با «تابع هدفی» (Objective Function) باشد که قرار است توسط الگوریتم‌های بهینه‌سازی بهینه شوند؛ چنین کاری به محققان اجازه می‌دهد تا بتوانند الگوریتم‌های بهینه‌سازی جدید را فرمول‌بندی و پیاده‌سازی کنند. در ادامه این مطلب، ابتدا مفاهیم مقدماتی و نحوه فرمول‌بندی کردن الگوریتم کرم شب تاب مورد بررسی قرار می‌گیرد. سپس، جزئیات مرتبط با پیاده‌سازی و تحلیل الگوریتم کرم شب تاب بررسی خواهد شد.

مفاهیم مرتبط با الگوریتم کرم شب تاب

در این بخش، جهت پیاده‌سازی الگوریتم بهینه‌سازی الهام گرفته شده از رفتار کرم شب تاب (Firefly-inspired Optimization Algorithm)، ویژگی‌های مشخصه مرتبط با رفتار کرم شتاب و الگوی نور چشمک‌زن تولید شده توسط آن‌ها فرمول‌بندی خواهد شد. جهت ساده‌سازی فرمول‌بندی کردن الگوریتم کرم شب تاب، از قواعد زیر استفاده می‌شود:

1. تمامی کرم‌های شب تاب، «تک جنسی» (Unisex) هستند. به عبارت دیگر، کرم‌های شب تاب، فارغ از جنسیت آن‌ها، مجذوب دیگر کرم‌های شب تاب موجود در فضای مسأله خواهند شد.
2. در الگوریتم کرم شب تاب (FA)، «جذابیت» (Attractiveness) یک کرم شب تاب متناسب با «روشنایی» (Brightness) آن کرم خواهد بود. به عبارت دیگر، به ازاء هر دو کرم شب تاب چشمک‌زن، کرمی که نور کمتری دارد به سمت کرمی که نور بیشتری دارد جذب خواهد شد. بنابراین، جذابیت کرم شب تاب، متناسب با روشنایی آن خواهد بود.
   • وقتی که فاصله بین دو کرم افزایش پیدا می‌کند، مقدار جذابیت (Attractiveness) و روشنایی (Brightness) آن‌ها کاهش پیدا می‌کند. به عبارت دیگر، وقتی که فاصله دو کرم شب تاب از یکدیگر بیشتر می‌شود، علاوه بر اینکه جذابیت آن‌ها برای یکدیگر کاهش پیدا می‌کند، روشنایی (قابل رؤیت) آن‌ها (برای یکدیگر) نیز کاهش پیدا می‌کند. در صورتی که روشنایی یک کرم شب‌تاب خاص از دیگر کرم‌ها بیشتر باشد، به طور تصادفی در محیط حرکت خواهد کرد (به سمت هیچ یک از کرم‌های دیگر جذب نخواهد شد).
3. روشنایی یک کرم شب تاب، از ویژگی‌های مشخصه تابع هدف تأثیر می‌پذیرد و یا به وسیله آن مشخص می‌شود. در مسائل «بیشنیه‌سازی» (Maximization)، روشنایی را می‌توان متناسب با مقدار «تابع برازندگی» (Fitness Function) مشخص کرد. شایان توجه است که این امکان وجود دارد که بتوان روشنایی کرم‌های شب تاب را، به شیوه‌ای مشابه با تابع برازندگی در «الگوریتم‌های ژنتیک» (Genetic Algorithms) تعریف کرد.

بر اساس این سه قاعده، می‌توان گام‌های اساسی مورد نیاز برای پیاده‌سازی الگوریتم کرم شب تاب را فرمول‌بندی کرد. گام‌های اساسی الگوریتم کرم شب تاب در «شبه کد» (Pseudo-Code) زیر نمایش داده شده است.

الگوریتم کرم شب تاب (Firefly Algorithm | FA)

• تابع هدف: $$f ( x ) , \; x = ( x _ { 1 } , . . . . . . . , x _{ d } ) ^ { T }$$.
• تولید جمعیت اولیه از کرم‌های شب تاب: $$x _ { i } , \; ( i = 1 , 2 , 3 , . . . . . , n )$$.
• پارامتر شدت نور $$I _ { i }$$ در $$x _ { i }$$، از طریق جای‌گذاری مقدار $$x _ { i }$$ در تابع $$f ( x _ { i } )$$ به دست می‌آید.
• تعریف کردن «ضریب جذب نور» (Light Absorption Coefficient) یا $$\gamma$$.
• حلقه While: تا زمانی که ( $$t < MaxGeneration$$ )
• حلقه For: ($$for\; i\;= 1 \; to \; n$$) به ازاء تمامی $$n$$ کرم‌ شب تاب موجود در جمعیت
  • حلقه For: ($$for\; j\;= 1 \; to \; i$$) به ازاء تمامی $$n$$ کرم‌ شب تاب موجود در جمعیت
    • شرط if: در صورتی که ($$I _ { j } > I _ { i }$$)، کرم شب تاب $$i$$ به سمت کرم شب تاب $$j$$ حرکت داده می‌شود (در فضای جستجوی d-بُعدی مسأله). پایان شرط if
    • مقدار پارامتر جذابیت (Attractiveness) بر اساس فاصله $$r$$ و مطابق با رابطه $$exp ( - \gamma r )$$ محاسبه و به‌روزرسانی می‌شود.
    • راه حل‌های (جواب‌های کاندید) جدید ارزیابی و پارامتر شدت نور (Light Intensity) به‌روزرسانی می‌شود.
  • پایان حلقه For.
• پایان حلقه For.
• کرم‌های شب تاب ارزیابی و بهترین جواب کاندید در این نسل (Generation) مشخص می‌شود.
• پایان حلقه While.
• جواب‌های نهایی «پس پردازش» (PostProcess) و مصورسازی‌های مرتبط با خروجی نهایی انجام می‌شود.

از جهات خاصی، شباهت‌های مفهومی میان الگوریتم کرم شب تاب (و الگوریتم‌های مشتق شده از آن) و «الگوریتم غذایابی باکتریایی» (Bacteria Foraging Algorithm | BFA) وجود دارد. الگوریتم غذایابی باکتریایی (Bacteria Foraging Algorithm) از رفتار جمعی باکتری‌ها در پیدا کردن منابع غذایی لازم برای بقاء الهام گرفته شده است. در الگوریتم BFA، بخشی از جذابیت میان باکتری‌ها (جذب شدن باکتری‌ها به سمت یکدیگر)، مبتنی بر «برازندگی» (Fitness) آن‌ها و بخش دیگر مبتنی بر فاصله میان آن‌ها است. در حالی که در الگوریتم کرم شب تاب (و نسخه‌های مختلف آن)، پارامتر جذابیت (Attractiveness) به تابع هدف و زوال (Decay) یکنواخت مقدار جذابیت، متناسب با افزایش فاصله میان کرم‌های شب تاب مرتبط است.

با این حال، با توجه به پراکندگی عوامل (منظور موجودیت‌های موجود در جمعیت یا همان کرم‌های شب تاب) موجود در الگوریتم کرم شب تاب در فضای جستجوی مسأله، قابل تنظیم بودن رؤیت‌پذیری عوامل نسبت به یکدیگر (بر اساس فاصله میان آن‌ها) و تنوع موجود در جمعیت با توجه به جذابیت متغیر عوامل نسبت به یکدیگر، انتظار می‌رود که الگوریتم کرم شب تاب بتواند به شکل بهتر و کارآمدتری، فضای جستجوی مسأله را مورد کاوش قرار دهد.

جذابیت (Attractiveness) در الگوریتم کرم شب تاب

در هنگام فرمول‌بندی کردن الگوریتم کرم شب تاب، نیاز است تا به دو مسأله اساسی توجه شود: «تغییرات شدت نور» (Variation of Light Intensity) و فرمول‌بندی کردن جذابیت متقابل کرم‌های شب تاب. برای ساده‌سازی فرآیند فرمول‌بندی کردن الگوریتم کرم شب تاب، می‌توان فرض کرد که جذابیت یک کرم شب تاب، بر اساس روشنایی این عامل (کرم شب تاب) مشخص می‌شود؛ که روشنایی کرم شب تاب نیز به نوبه خود، به تابع هدف «کدبندی شده» (Encoded) جهت حل یک مسأله خاص مرتبط است.

در ساده‌ترین حالت و برای یک مسأله بیشینه‌سازی، می‌توان مقدار پارامتر روشنایی $$I$$ یک کرم شب تاب را، که در مکان خاص $$X$$ قرار دارد، از طریق رابطه‌ای نظیر $$I ( X ) \propto f ( x )$$ به دست آورد. با این حال، مقدار پارامتر جذابیت $$\beta$$ یک کرم شب تاب نسبی است و باید توسط دیگر کرم‌ها مشخص شود (به عبارت دیگر، فاصله میان کرم‌های شب تاب، نقش مستقیمی در جذابیت آن‌ها (جذب آن‌ها به سمت یکدیگر) خواهد داشت). بنابراین، پارامتر جذابیت $$\beta$$، بر اساس فاصله $$r _ { i j }$$ میان کرم شب تاب $$i$$ و کرم شب تاب $$j$$، تغییر پیدا خواهد کرد.

علاوه بر این، هر چقدر که فاصله از منبع نور بیشتر شود، شدت نور (Light Intensity) کاهش پیدا می‌کند. همچنین، نور هنگام گذر از «واسط‌هایی» (Medium) نظیر هوا، توسط آن جذب می‌شود.در نتیجه، الگوریتم کرم شب تاب باید به گونه‌ای فرمول‌بندی شود که بر اساس «درجات جذب» (Degrees of Absorption) مختلف، مقدار پارامتر جذابیت (Attractiveness) نیز تغییر پیدا کند.

در ساده‌ترین حالت ممکن، پارامتر شدت نور $$I ( r )$$ بر اساس «قانون مربع معکوس» (Inverse Square Law) تغییر پیدا خواهد کرد:

$$I ( r ) = \frac { I _ { s } } { r ^ { 2 } }$$

در این قانون، پارامتر $$I _ { s }$$ شدت نور در منبع را نشان می‌دهد. با در اختیار داشتن یک واسط (نظیر هوا) با ضریب ثابتِ جذب نور، $$\gamma$$، شدت نور $$I$$، بر اساس فاصله $$r$$ و از طریق رابطه زیر تغییر پیدا خواهد کرد:

$$I = { I _ { 0 } } e ^ { - \gamma r }$$

در این رابطه، $$I _ { 0 }$$ شدت نور اصلی را نشان می‌دهد. برای اجتناب از رخ دادن «تکینی» (Singularity) در رابطه $$\frac { I _ { s } } { r ^ { 2 } }$$ و در نقطه $$r=0$$، می‌توان «اثر ترکیبی» (Combined Effect) قانون مربع معکوس و اصل جذب نور توسط واسط هوا را با استفاده از تابع زیر (که به فرم گاوسی (Gaussian) است) تقریب زد:

$$I ( r ) = { I _ { 0 } } e ^ { -\gamma r ^ { 2 } }$$

بعضی مواقع به تابعی نیاز است که بتواند به طور یکنواخت و با نرخ آهسته‌تری کاهش پیدا کند. در چنین حالتی، می‌توان از «تقریب» (Approximation) زیر استفاده کرد:

$$I ( r ) = \frac { I _ { 0 } } {1 + \gamma r ^ { 2 } }$$

در یک فاصله کوتاه (فاصله بین دو کرم شب تاب بسیار کم باشد)، دو فرم ارائه شده از تابع $$I ( r )$$ تقریبا با یکدیگر برابر هستند. چنین پدیده‌ای به این دلیل است که برای مقدار $$r=0$$، «بسط‌های سری» (Series Expansions) این دو تابع، تا مرتبه $$O ( r ^ 3 )$$، معادل یکدیگر خواهند بود:

$$\frac { 1 } {1 + \gamma r ^ { 2 } } \approx 1 - \gamma r ^ { 2 } + \frac { 1 } { 2 } \gamma ^ 2 r ^ { 4 } + . . . .$$

$$e^{ -\gamma r ^ { 2 } } \approx 1 - \gamma r ^ { 2 } + \frac { 1 } { 2 } \gamma ^ 2 r ^ { 4 } + . . . .$$

از آنجایی که جذابیت یک کرم شب تاب، متناسب با شدت نوری است که توسط کرم‌های شب تاب مجاور (همسایه) مشاهده می‌شود، پارامتر جذابیت $$\beta$$ یک کرم شب تاب را می‌توان از طریق رابطه زیر تعریف کرد:

$$\beta ( r ) = \beta _ { 0 } e ^ { -\gamma r ^ { 2 } }$$

در این رابطه، $$\beta _ { 0 }$$ برابر با جذابیت کرم شب تاب در فاصله $$r=0$$ است. از آنجایی که محاسبه رابطه $$\frac { 1 } { ( 1 + r ^ { 2 } ) }$$ از محاسبه یک «تابع نمایی» (Exponential Function) سریع‌تر است، به جای تابع بالا می‌توان از تابع زیر استفاده کرد و مقدار پارامتر جذابیت را از طریق رابطه زیر محاسبه کرد:

$$\beta ( r ) = \frac { \beta _0 } { 1 + \gamma r ^ { 2 } }$$

رابطه بالا، پارامتری به نام فاصله مشخصه (Characteristic Distance) یا مقیاس طول (Length Scale) را به صورت $$\Gamma = \frac { 1 } { \sqrt { \gamma } }$$ تعریف می‌کند که توسط آن، پارامتر جذابیت، به طرز قابل ملاحظه‌ای از فرم $$\beta _0$$، به فرم $$\beta _ 0 e ^ { - 1 }$$ تغییر پیدا می‌کند.

در هنگام پیاده‌سازی الگوریتم کرم شب تاب (و نسخه‌های مختلف آن)، تابع $$\beta ( r )$$ می‌تواند به شکل «توابع نزولی یکنواخت» (Monotonically Decreasing Functions)، نظیر شکل «تعمیم داده شده» (Generalized) زیر نمایش داده شود:

$$\beta ( r ) = \beta _ { 0 } e ^ { -\gamma r ^ { m } }, \; ( m \geq 1 )$$

در صورتی که پارامتر $$\gamma$$ ثابت فرض شود، وقتی که $$m \rightarrow \infty$$، پارامتر فاصله مشخصه یا مقیاس طول به شکل $$\Gamma = \gamma ^ { \frac { -1 } { m } }$$ تغییر پیدا می‌کند. متقابلا، با در اختیار داشتن مقدار پارامتر فاصله مشخصه یا مقیاس طول در یک مسأله بهینه‌سازی، پارامتر $$\Gamma$$ می‌تواند به شکل $$\gamma = \frac { 1 } { \Gamma ^ { m } }$$ و به عنوان یک «مقدار اولیه» (Initial Value) معمولی مورد استفاده قرار بگیرد.

فاصله (Distance) و «حرکت» (Movement) در الگوریتم کرم شب تاب

فاصله (Distance) میان دو کرم شب تاب $$i$$ و $$j$$، که به ترتیب در مختصات مکانی $$x _ { i }$$ و $$x _ { j }$$ قرار دارند، برابر با «فاصله دکارتی» (Cartesian Distance) میان آن‌ها به فرم زیر است:

$$r _ { i j } = \parallel x _ { i } - x _ { j } \parallel = \sqrt { \sum _ d ^ { k = 1 } ( x _ { i , k} - x _ { j , k } ) ^ { 2 } }$$

در این رابطه، $$x _ { i , k}$$ برابر با $$k$$-اُمین مؤلفه مختصات مکانی مرتبط با $$i$$-اُمین کرم شب تاب ($$x _ { i }$$) است. در یک فضای جستجوی دوبُعدی، فاصله میان دو کرم شب تاب $$i$$ و $$j$$ از طریق رابطه زیر محاسبه می‌شود:

$$r _ { i j } = \parallel x _ { i } - x _ { j } \parallel = \sqrt { (x _ { i } - x _ { j } ) ^ { 2 } - (y _ { i } - y _ { j } ) ^ { 2 } }$$

حرکت (Movement) کرم شب تابی (به عنوان نمونه، کرم شب تاب $$i$$) که جذب یک کرم شب تاب جذاب‌تر (روشن‌تر) دیگر شده است، از طریق رابطه زیر مشخص می‌شود:

$$x _ { i } = x _ { i } + \beta _ { 0 } e ^ { - \gamma r _ { i j } ^ { 2 } } (x _ { j } - x _ { i } ) + \alpha \; (rand - \frac { 1 } { 2 } )$$

در اینجا، عبارت دوم سمت راست رابطه، تأثیر پارامتر جذابیت را در محاسبه مقدار حرکت کرم شب تاب $$i$$ نشان می‌دهد. همچنین، عبارت سوم جهت تصادفی‌سازی (Randomization) به کار می‌رود که در آن $$\alpha$$ نقش پارامتر تصادفی‌سازی را ایفا می‌کند. عبارت rand نیز یک «مولد اعداد تصادفی» (Random Number Generator) است که مقادیر تصادفی تولید شده توسط آن، از «توزیع یکنواخت» (Uniform Distribution) در بازه $$\left [ 0 , \; 1 \right ]$$ تبعیت می‌کنند.

در پیاده‌سازی‌های انجام شده از الگوریتم کرم شب تاب جهت حل مسائل بهینه‌سازی، مقدار پارامتر $$\beta _ { 0 } = 1$$ در نظر گرفته شده است و مقدار پارامتر $$\alpha$$، از بازه $$\alpha \in \left[0,\;1\right]$$ انتخاب می‌شود. علاوه بر این، مقدار عبارت تصادفی‌سازی (عبارت سوم در رابطه بالا) را می‌توان بر اساس یک «توزیع نرمال» (Normal Distribution) به فرم $$N ( 0 , \;1 )$$ یا هر توزیع دلخواه دیگر محاسبه کرد.

همچنین، در شرایطی که مقیاس‌های عددی متغیرهای مسأله تفاوت فاحشی با یکدیگر داشته باشند، به عنوان نمونه، مقیاس عددی یکی از متغیرهای مسأله برابر با $$\left [ 10 ^ { -5 } , \; 10 ^ { 5 } \right ]$$ باشد و مقیاس عددی یک متغیر دیگر، برابر یا $$\left [ -0.01 , \; 0.01 \right ]$$ باشد، در چنین حالتی، بهتر است که پارامتر $$\alpha$$ در عبارت تصادفی‌سازی، با پارامتر $$\alpha S_{k}$$ جا به جا شود. مؤلفه‌های $$S_{k}$$ در این پارامتر، بردار «پارامترهای مقیاس‌گذاری» (Scaling Parameters) نام دارد. در صورتی که مسأله بهینه‌سازی مد نظر d-ُبعدی باشد، پارامترهای مقیاس‌گذاری $$S _ { k } ( K = 1 , 2 , . . . , d )$$ باید بر اساس مقیاس‌های واقعی مسأله بهینه‌سازی مورد نظر مشخص شوند.

در رابطه مشخص کردن حرکت (Movement) کرم‌های شب تاب، پارامتر $$\gamma$$، تغییرات جذابیت کرم‌های شب تاب در الگوریتم کرم شب تاب را مشخص می‌کند. همچنین، مقدار این پارامتر نقش بسیار مهمی در مشخص کردن سرعت همگرایی، رفتار الگوریتم کرم شب تاب در جستجوی فضای مسأله و حل مسأله بهینه‌سازی داده شده دارد. در تئوری، مقدار پارامتر $$\gamma$$ از طریق $$\gamma \in \left [ 0,\; \infty \right)$$ مشخص می‌شود، ولی در عمل، این پارامتر به وسیله $$\gamma = O (1)$$ مقداردهی می‌شود؛ این مقدار به وسیله پارامتر فاصله مشخصه یا مقیاس طول (پارامتر $$\Gamma$$) سیستمی که قرار است بهینه‌سازی شود، مشخص می‌شود. بنابراین، در بیشتر کاربردها، این پارامتر معمولا مقداری بین $$0.01$$ و $$100$$ به خود می‌گیرد.

مقیاس‌گذاری (Scaling) مسائل بهینه‌سازی و تجزیه و تحلیل مجانبی

شایان ذکر است که محاسبه فاصله $$r$$ در الگوریتم کرم شب تاب (و پیاده‌سازی‌های مختلف آن)، که در بخش قبل توضیح داده شد، محدود به استفاده از «فاصله اقلیدسی» (Euclidean Distance) نیست و می‌توان از هر معادله دلخواهی برای محاسبه فاصله میان کرم‌های شب تاب استفاده کرد. به عبارت دیگر، بسته به نوع مسأله بهینه‌سازی که قرار است توسط الگوریتم کرم شب تاب حل شود، می‌توان معادلات مختلفی را برای محاسبه فاصله $$r$$ در فضای n-بُعدی  استفاده کرد.

به عنوان نمونه، در مسائل «زمان‌بندی کار» (Job Scheduling)، فاصله $$r$$ می‌تواند به عنوان پارامتر «تأخیر زمانی» (Time Lag) و یا «بازه زمانی» (Time Interval) تعریف شود. همچنین، در شبکه‌های پیچیده نظیر اینترنت و «شبکه‌های اجتماعی» (Social Networks)، که مسائل در قالب «گراف» (Graph) نمایش داده می‌شوند، فاصله $$r$$ را می‌توان به عنوان ترکیبی از «درجه خوشه‌بندی محلی» (Degree of Local Clustering) و «متوسط نزدیکی رأس‌ها» (Average Proximity of Vertices) تعریف کرد. به عبارت دیگر، هر معیاری که به شکل مؤثر بتواند مقادیر مطلوب و مورد نظر در مسأله بهینه‌سازی را مشخص کند، می‌تواند به عنوان فاصله $$r$$ تعریف شود.

مقدار پارامتر مقیاس طول (پارامتر $$\Gamma$$)، باید متناسب با مقیاس مسأله بهینه‌سازی مورد نظر، در الگوریتم کرم شب تاب در نظر گرفته شود. در صورتی که $$\Gamma$$، مقیاس مسأله بهینه‌سازی مورد نظر برای یک جمعیت متشکل از تعداد زیادی کرم شب تاب ($$n \gg m$$، در اینجا $$n$$ تعداد کرم‌های شب در الگوریتم کرم شب تاب و $$m$$ تعداد «بهینه‌های محلی» (Local Optimums) را نشان می‌دهد) باشد، بهتر است که مکان‌های اولیه $$n$$ کرم شب تاب موجود در جمعیت، به شکل نسبتا یکنواختی در فضای جستجوی (Search Space) توزیع شده باشند؛ توصیه می‌شود که نحوه توزیع شدگی کرم‌های شب تاب در فضای جستجوی مسأله (مقداردهی اولیه جمعیت در الگوریتم کرم شب تاب)، تا حدودی شبیه به مقداردهی اولیه (Initialization) در «شبیه‌سازی‌های مونته کارلو» (Monte-Carlo Simulations) باشد.

هر چقدر که تعداد تکرارهای (نسل) بیشتری از الگوریتم کرم شب تاب انجام می‌شود، کرم‌های شب تاب به شیوه‌ای تصادفی، به بهینه‌های محلی (از جمله بهینه‌های سراسری؛ بهینه سراسری در مسائل بهینه‌سازی، زیر مجموعه‌‌ای از بهینه‌های محلی محسوب می‌شوند) مسأله بهینه‌سازی مورد نظر همگرا می‌شوند. با مقایسه بهترین جواب‌ها در میان بهینه‌های محلی، جواب بهینه سراسری مسأله بهینه‌سازی توسط الگوریتم کرم شب تاب مشخص می‌شود.

در این بخش، هدف ثابت کردن این موضوع است که وقتی $$n \rightarrow \infty$$ و $$t \gg 1$$ باشد، الگوریتم کرم شب به جواب بهینه سراسری مسأله بهینه‌سازی مورد نظر همگرا می‌شود (در اینجا، $$n$$ برابر با تعداد کرم‌های شب تاب در جمعیت اولیه و $$t$$ برابر با تعداد نسل‌های (تکرار) الگوریتم کرم شب تاب است). در آزمایشات عملی انجام شده رو توابع بهینه‌سازی مرجع، الگوریتم کرم شب تاب عملکرد بسیار خوبی از خود نشان می‌دهد؛ به گونه‌ای که در کمتر از 50 تا 100 تکرار (نسل)، این الگوریتم به جواب بهینه سراسری همگرا می‌شود. نتایج ارزیابی الگوریتم کرم شب تاب با استفاده از «توابع بهینه‌سازی معیار» (Benchmark Functions)، در بخش‌های بعدی نمایش داده خواهد شد.

برای اثبات همگرایی الگوریتم کرم شب تاب به جواب بهینه سراسری، دو مورد محدود کننده مهم باید مورد بررسی قرار گرفته شوند:

• زمانی که $$\gamma \rightarrow 0$$، پارامتر $$\gamma$$ به سمت صفر میل می‌کند.
• زمانی که $$\gamma \rightarrow \infty$$، پارامتر $$\gamma$$ به سمت بی‌نهایت میل می‌کند.

در حالتی که $$\gamma \rightarrow 0$$، پارامتر $$\gamma$$ به سمت صفر میل می‌کند، پارامتر جذابیت مقداری ثابت و برابر صفر خواهد بود ($$\beta = \beta_{0}$$) و پارامتر مقیاس به سمت بی‌نهایت میل می‌کند ($$\Gamma \rightarrow \infty$$). چنین پدیده‌ای را می‌توان به این شکل تصور کرد که شدت نور (Light Intensity) کرم‌های شب تاب در آسمان کاهش پیدا نخواهد کرد. به عبارت دیگر، یک کرم شب تاب چشمک‌زن در هر نقطه‌ای از ناحیه مورد نظر (معادل فضای جستجوی مسأله) قابل رؤیت خواهد بود. بنابراین، الگوریتم کرم شب تاب به راحتی قادر خواهد بود به یک نقطه «بهینه» (Optimum) در فضای جستجوی مسأله همگرا شود (معمولا این بهینه، همان بهینه سراسری مسأله خواهد بود). وقتی که $$\gamma \rightarrow 0$$، پارامتر $$\gamma$$ به سمت صفر میل می‌کند، الگوریتم کرم شب تاب متناظر با الگوریتم بهینه‌سازی ازدحام ذرات (PSO) خواهد بود. همچنین، عملکرد و کارایی این حالت خاص از الگوریتم کرم شب تاب، همانند الگوریتم PSO خواهد بود.

در حالتی که $$\gamma \rightarrow \infty$$، پارامتر $$\gamma$$ به سمت بی‌نهایت میل می‌کند، $$\beta ( r ) \rightarrow \delta ( r )$$ («تابع دلتای دیراک» (Dirac Delta Function)) و پارامتر مقیاس به سمت صفر میل می‌کند ($$\Gamma \rightarrow 0$$). این بدین معنی است که جذابیت یک کرم شتاب، برای دیگر کرم‌های شب تاب موجود در محیط (فضای جستجوی مسأله) صفر است و یا اینکه کرم‌های شب تاب «نزدیک بین» (Short-Sighted) هستند. چنین پدیده‌ای معادل پرواز کردن کرم‌های شب تاب در یک ناحیه مه‌آلود (Foggy)، به صورت کاملا تصادفی است. در چنین حالتی، دیگر کرم‌های شب تاب نیز قابل رؤیت نخواهند بود و هر کرم شب تاب، به طور کاملا تصادفی در محیط پرسه می‌زند. بنابراین در چنین شرایطی، الگوریتم کرم شب تاب به یک روش «جستجوی کاملا تصادفی» (Completely Random Search) تبدیل می‌شود.

این دو مورد، حالات بسیار خاص از الگوریتم کرم شب تاب محسوب می‌شوند؛ به عبارت دیگر، نقاط حداکثری (Extremes) و استثناء در الگوریتم کرم شب تاب محسوب می‌شوند. به طور کلی، الگوریتم کرم شب تاب همیشه بین این دو حالت خاص قرار می‌گیرد. همچنین، با تنظیم مناسب پارامترهای $$\gamma$$ و $$\alpha$$، الگوریتم کرم شب تاب قادر خواهد بود عملکرد بهتری نسبت به الگوریتم بهینه‌سازی ازدحام ذرات (PSO) و روش جستجوی تصادفی (Random Search) از خود نشان دهد.

یکی از ویژگی‌های مهم الگوریتم کرم شب تاب این است که می‌تواند به شکل بسیار مؤثری، علاوه بر یافتن «بهینه سراسری» (Global Optimum)، به طور همزمان بهینه‌های محلی مسائل بهینه‌سازی را نیز پیدا کند. چنین مزیت مهمی در الگوریتم کرم شب تاب (در طول فرایند بهینه‌سازی توابع هدف یک مسأله بهینه‌سازی خاص)، در بخش‌های بعدی نمایش داده می‌شود.

مزیت دیگر الگوریتم کرم شب که آن را از دیگر الگوریتم‌های بهینه‌سازی مرسوم متمایز می‌کند این است که کرم‌های شب تاب مختلف، تقریبا مستقل از یکدیگر عمل می‌کنند. چنین ویژگی مهمی، الگوریتم کرم شب تاب را به انتخابی ایده‌آل برای «پیاده‌سازی‌های موازی» (Parallel Implementation) از الگوریتم‌های تکاملی تبدیل می‌کند. همچنین، از آنجایی که کرم‌های شب تاب به شکل فشرده‌تری حول بهینه‌های (Optimums) موجود در فضای جستجوی مسأله جمع می‌شوند، بهتر از الگوریتم ژنتیک و الگوریتم بهینه‌‌سازی ازدحام ذرات عمل می‌کنند (به عنوان نمونه، کروموزم‌های تعریف شده در الگوریتم ژنتیک، در اثر عملگرهای تکاملی به ویژه عملگر ترکیب یا آمیزش، در فضای جستجو پرش می‌کنند، در حالی که در الگوریتم کرم شب تاب چنین فرایندی مشاهده نمی‌شود). در پیاده‌سازی موازی صورت گرفته از الگوریتم کرم شب تاب، تعامل میان «زیر ناحیه‌ها» (Subregions) به حداقل می‌رسد.

بهینه‌سازی چندمُدی با بهینه‌های چندگانه

برای اینکه نحوه کارکرد الگوریتم شب تاب در بهینه‌سازی توابع مورد بررسی قرار بگیرد، از توابع معیار مختلفی استفاده شده است تا صحت عملکرد این الگوریتم سنجیده شود (نتایج حاصل از ارزیابی عملکرد الگوریتم کرم شب تاب در ادامه نمایش داده شده است). همچنین، کدهای پیاده‌سازی این الگوریتم در زبان‌های برنامه‌نویسی مختلف نمایش داده خواهد شد.

ارزیابی و سنجش عملکرد الگوریتم کرم شب تاب

در این مطلب، به عنوان نمونه، از الگوریتم کرم شب تاب برای پیدا کردن بهینه سراسری تابع Michalewicz استفاده می‌شود. فرم ریاضی تابع Michalewicz، به شکل زیر است:

$$f ( x ) = - \sum _ { i = 1 } ^ d \sin ( x _ { i } ) \left [ \sin ( \frac { i x _ i ^ 2 } { \pi } ) \right ] ^ { 2m }$$

در این تابع، $$m=10$$ و $$d = 1 , 2 , . . . .$$ است. بهینه سراسری تابع، $$f _ { * } \approx -1.0801$$، در یک فضای دوبُعدی، در نقطه $$(2.20319, 1.57049)$$ رخ می‌دهد. نقطه بهینه سراسری تابع Michalewicz، پس از 10 تکرار الگوریتم کرم شب تاب و به ازاء 40 کرم شب تاب موجود در جمعیت (تابع، حدودا 400 بار، برای یافتن نقطه بهینه ارزیابی می‌شود) یافت خواهد شد. در این شبیه‌سازی (بهینه‌سازی و ارزیابی تابع هدف Michalewicz با استفاده از الگوریتم کرم شب تاب)، مقادیر پارامترها برابر با $$\alpha=0.2$$، $$\gamma=1$$ و $$\beta_{0}=1$$ در نظر گرفته شده‌اند.

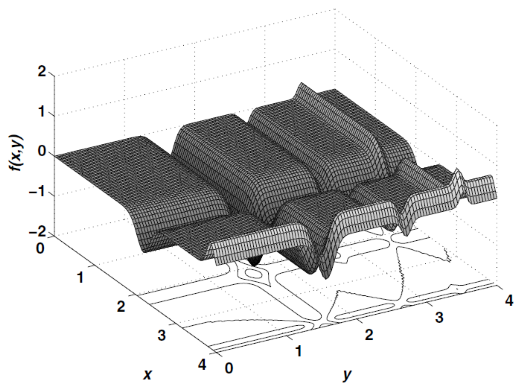
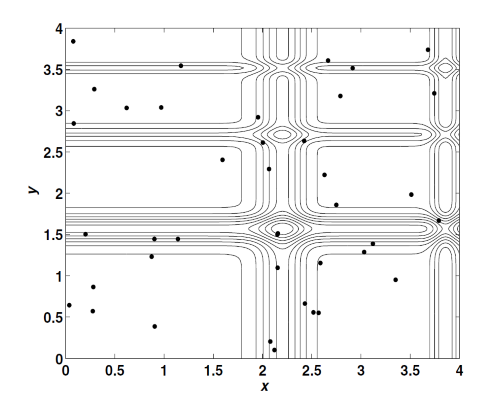
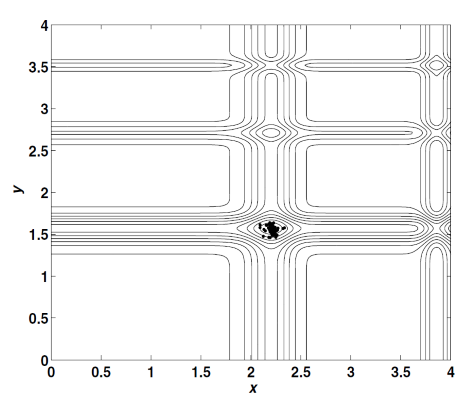
در مرحله بعد عملکرد الگوریتم کرم شب تاب در پیدا کردن نقطه بهینه سراسری توابع سخت‌تر و پیچیده‌تر ارزیابی می‌شود. نتایج ارزیابی روی این دسته از توابع نشان می‌دهد که الگوریتم کرم شب تاب عملکرد بهتری نسبت به دیگر الگوریتم‌های فرا اکتشافی موجود دارد. به عنوان نمونه، از الگوریتم کرم شب تاب برای پیدا کردن بهینه سراسری تابع Yang استفاده می‌شود. این تابع، یک تابع چندمُدی است که الگویی شبیه به یک موج ایستاده دارد. فرم ریاضی تابع Yang، به شکل زیر است:

$$f (x) = \left [ e ^ { -\sum _ { i = 1 } ^ d ( x _ { i } / a ) ^ { 2 m } } - 2 e ^ { - \sum _ { i = 1 } ^ d x _ { i } ^ { 2 } } \right ] \cdot \prod _ { i = 1 } ^ d \cos ^ { 2 } x _ { i } , \; \; \; \; \; m = 5$$

همانطور که در شکل زیر مشهود است، این تابع چندمُدی، چندین بهینه محلی (کمینه (Valley) و بیشینه (Peak) محلی) دارد. نقطه بهینه سراسری این تابع، $$f_{\star}=-1$$، در نقطه $$(0,0,....,0)$$ و در ناحیه $$-20 \leq x _ { i } \leq 20$$ قرار دارد. در این تابع، $$i=1, 2, ...., d$$ و $$a=15$$ است. نمایش سه‌بُعدی تابع Yang در شکل زیر ارائه شده است.

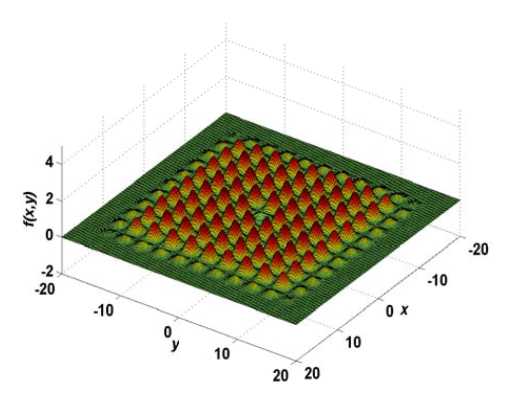
مقایسه الگوریتم کرم شب تاب با الگوریتم ژنتیک و PSO

مطالعات مختلف نشان می‌دهد که الگوریتم بهینه‌سازی ازدحام ذرات (PSO) می‌تواند عملکرد به مراتب بهتری نسبت به الگوریتم ژنتیک (GA) و الگوریتم‌های بهینه‌سازی مرسوم، در حل بسیاری از  مسائل بهینه‌سازی از خود نشان دهد. یک دلیل محتمل برای عملکرد بهینه الگوریتم بهینه‌سازی ازدحام ذرات، توانایی بهترین تخمین یافت شده از جواب بهینه (در هر مرحله)، در مخابره کردن (Broadcasting) یا ارتباط برقرار کردن با دیگر ذرات موجود در جمعیت است؛ چنین ویژگی مهمی سبب می‌شود تا الگوریتم به شکل بهتر و سریع‌تری به جواب بهینه سراسری همگرا شود.

در این مرحله، نتایج ارزیابی الگوریتم کرم شب تاب و مقایسه آن با نتایج حاصل از الگوریتم ژنتیک و PSO نمایش داده می‌شود. برای چنین کاری، از توابع معیار استاندارد استفاده شده است.

برای پیاده‌سازی و ارزیابی الگوریتم ژنتیک و مقایسه آن با الگوریتم کرم شب تاب، از الگوریتم ژنتیک استاندارد استفاده شده است؛ در الگوریتم ژنتیک استاندارد از اصل «نخبه‌گرایی یا الیتیسم» (Elitism) استفاده نشده است. «احتمال جهش» (Mutation Probability | $$p_{m}$$) برابر با $$p_{m}=0.05$$ و «احتمال ترکیب» (Crossover Probability | $$p_{c}$$) برابر با $$p_{c}=0.95$$ در نظر گرفته شده است.

برای پیاده‌سازی و ارزیابی الگوریتم بهینه‌سازی ازدحام ذرات (PSO) و مقایسه آن با الگوریتم کرم شب تاب، از نسخه استاندارد الگوریتم PSO استفاده شده است. در الگوریتم استاندارد بهینه‌سازی ازدحام ذرات، از پارامترهای یادگیری $$\alpha \approx \beta \approx2$$ استفاده شده است و ویژگی «تصحیح اینرسی» (Inertia Correction) به کار گرفته نشده است.

در مرحله ارزیابی و مقایسه عملکرد الگوریتم کرم شب تاب با دیگر الگوریتم‌های بهینه‌سازی مشابه، مقادیر متفاوتی برای اندازه جمعیت در نظر گرفته شد ($$n = 15 \; to \; 200$$). با این حال، در بیشتر شبیه‌سازی‌های انجام شده و برای غالب توابع استفاده شده، مقدار $$n = 15 \; to \; 50$$، به عنوان مناسب‌ترین مقدار برای اندازه جمعیت مشخص شد. بنابراین، از مقدار ثابت $$n = 40$$، به عنوان اندازه جمعیت، در تمامی شبیه‌سازی‌ها و ارزیابی‌ها استفاده شده است.

برای اینکه تحلیل‌های آماری معناداری روی نتایج حاصل از ارزیابی الگوریتم‌ها انجام شود، پس از پیاده‌سازی الگوریتم‌ها، شبیه‌سازی‌های گسترده‌ای روی آن‌ها انجام شد و هر کدام از الگوریتم‌ها حداقل 100 بار اجرا شدند. اجرای الگوریتم‌ها تنها زمانی متوقف می‌شود که تغییرات مقادیر توابع معیار، از یک حد آستانه داده شده، $$\epsilon \leq 10^{-5}$$ کمتر باشند. نتایج حاصل از شبیه‌سازی‌های انجام شده و مقایسه عملکرد الگوریتم‌های تکاملی در جدول زیر نمایش داده شده است.

فرم ریاضی توابع مشخص شده در جدول زیر، در ادامه نمایش داده شده است:

فرم ریاضی تابع Michalewicz:

$$f ( x ) = - \sum _ { i = 1 } ^ d \sin ( x _ { i } ) \left [ \sin ( \frac { i x _ i ^ 2 } { \pi } ) \right ] ^ { 2m }$$

فرم ریاضی تابع Yang:

$$f (x) = \left [ e ^ { -\sum _ { i = 1 } ^ d ( x _ { i } / a ) ^ { 2 m } } - 2 e ^ { - \sum _ { i = 1 } ^ d x _ { i } ^ { 2 } } \right ] \cdot \prod _ { i = 1 } ^ d \cos ^ { 2 } x _ { i } , \; \; \; \; \; m = 5$$

فرم ریاضی تابع Rosenbrock:

$$f ( x ) = \sum _ { i = 1 } ^ { n - 1 } \left [ 100 \left ( x _ { i + 1 } - x ^ 2 _ i \right ) ^ 2 + \left ( x _ i - 1 \right ) ^ 2 \right ]$$

فرم ریاضی تابع De Jong:

$$f ( x ) = \sum _ { i = 1 } ^ n x _ i ^ 2 \;\;\;\; -5.12 \leq x _ i \leq 5.12$$

فرم ریاضی تابع Schwefel:

$$f ( x ) = \sum _ { i = 1 } ^ n -x _ i . \sin ( \sqrt { | x _ i |}) \;\;\;\; -500 \leq x _ i \leq 500$$

فرم ریاضی تابع Ackley:

$$f ( x ) = - 20 \ e ^ { \displaystyle \left ( -0.2 \times \sqrt { \frac { 1 } { n } \sum _ { i = 1 } ^ { n } x ^ 2 _ i } \right ) } - e ^ { \displaystyle \left [ \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \cos ( 2 \pi x _ i ) \right ] } + 20 + e ^ { 1 }$$

فرم ریاضی تابع Rastrigin:

$$f (x) = 10n+ \sum_{i=1}^{n} (x_i^2 - 10 \cos (2\pi x_{i})), n=9$$

$$-5.12\leq x_{i} \leq 5.12, f(0,0,....,0)=0$$

فرم ریاضی تابع Easom:

$$f ( x ) = -\cos \left ( x _ 1 \right ) \cos \left ( x _ 2 \right ) e ^ { \displaystyle \left [ - \left ( x _ 1 - \pi \right ) ^ 2 - \left ( x _ 2 -\pi \right ) ^ 2 \right ] }$$

فرم ریاضی تابع Griewank:

$$f ( x ) = \frac { 1 } { 4000 } \sum _ { i = 1 } ^ { n } x ^ 2 _ i - \prod _ { i = 1 } ^ { n } \cos \left ( \frac { x _ i } { \sqrt { i } } \right ) + 1$$

فرم ریاضی تابع Shubert:

$$f ( x ) = \sum ^ 5 _ { i = 1 } i \sin \left [ ( i + 1 ) x + i \right ]$$

اعداد نمایش داده شده در جدول زیر به این فرم هستند:

[ تعداد متوسط ارزیابی‌های تابعی انجام شده ± انحراف از معیار (نرخ موفقیت الگوریتم) ]

بنابراین وقتی امتیاز عملکرد الگوریتم کرم شب تاب در بهینه‌سازی تابع Michalewicz به شکل $$3752 ± 725(99\%)$$ نمایش داده شده باشد، به چه معناست؟. این بدین معنی است که تعداد متوسط ارزیابی‌های تابعی انجام شده توسط الگوریتم کرم شب تاب برابر با 3572 است و انحراف معیار آن برابر با 725 است. همچنین، نرخ موفقیت الگوریتم شب تاب در همگرایی به نقطه بهینه سراسری برابر با 99 درصد است.

همانطور که در جدول بالا قابل مشاهده است، الگوریتم کرم شب تاب، کارآیی به مراتب بهتری نسبت به الگوریتم ژنتیک و الگوریتم بهینه‌سازی ازدحام ذرات (PSO) از خود نشان می‌دهد. همچنین، نرخ موفقیت الگوریتم کرم شب تاب در همگرایی به جواب بهینه سراسری به مراتب بالاتر از دیگر الگوریتم‌ها است. در سیستم‌های محاسبات امروزی (لپ‌تاپ، کامپیوتر شخصی و سایر موارد)، ارزیابی عملکرد الگوریتم‌ها در بهینه‌سازی توابع، تقریبا به صورت «آنی» (Instantaneous) انجام می‌شود.

به عنوان نمونه، انجام 10 هزار ارزیابی تابعی روی یک پردازنده‌ (کامپیوترهای شخصی)، چیزی حدود 5 ثانیه زمان می‌برد. حتی با در نظر گرفتن امکانات گرافیکی جهت نمایش مکان کرم‌های شب تاب (نمونه‌های موجود در جمعیت) در فضای جستجو، به صورت تعاملی، اجرای الگوریتم تنها چیزی حدود چند دقیقه زمان خواهد برد.

شایان ذکر است که این امکان وجود دارد که بتوان از روش‌های رسمی «آزمون فرض آماری» (Statistical Hypothesis Testing) جهت صحت‌سنجی «معنادار بودن» (Significance) نتایج حاصل استفاده کرد.

پیاده‌سازی الگوریتم کرم شب تاب در زبان‌های برنامه‌نویسی مختلف

در این بخش، کدهای پیاده‌سازی الگوریتم کرم شب تاب در زبان‌های برنامه‌نویسی مختلف ارائه می‌شود

پیاده‌سازی الگوریتم کرم شب تاب در زبان متلب

در این بخش، کدهای پیاده‌سازی مؤلفه‌های مختلف الگوریتم کرم شب تاب در زبان متلب ارائه می‌شود. در ابتدا، کدهای پیاده‌سازی استاندارد الگوریتم کرم شب تاب نمایش داده خواهد شد.

کدهای پیاده‌سازی استاندارد الگوریتم کرم شب تاب

کدهای پیاده‌سازی شده (کدهای بالا) را می‌توان برای بهینه‌سازی توابع چندمُدی و چندبُعدی مورد استفاده قرار داد. در کدهای نشان داده شده، جهت نمایش عملکرد پیاده‌سازی استاندارد الگوریتم کرم شب تاب در بهینه‌سازی توابع مختلف، یک تابع دوبُعدی با چهار بیشینه (Peak) تدارک دیده شده است؛ از میان چهار بیشینه نمایش داده شده در شکل زیر، یکی از آن‌ها، بهینه سراسری (Global Optimum) و سه بیشینه دیگر، بهینه محلی (Local Optimum) هستند.

در این بخش، هدف، نمایش قابلیت الگوریتم کرم شب تاب در بهینه‌سازی توابع و یافتن همزمان بهینه‌های محلی و سراسری توابع بهینه‌سازی است. مقادیر حد بالا و حد پایین متغیرهای مسأله، به ترتیب 5 و 5- در نظر گرفته شده‌اند. عامل تصادفی‌سازی $$\alpha$$ برابر با 0٫۲ و پارامتر $$\gamma$$ (پارامتر ضریب جذب) نیز برابر با 1 خواهد بود. همچنین، پارامتر جذابیت، از طریق رابطه $$\beta=exp(-\gamma r)$$ به دست می‌آید. اجرای الگوریتم تنها زمانی متوقف می‌شود که تغییرات مقادیر توابع معیار، از یک حد آستانه داده شده کمتر و یا اینکه الگوریتم، به تعداد بیشینه تکرارهای (نسل) مجاز رسیده باشد.

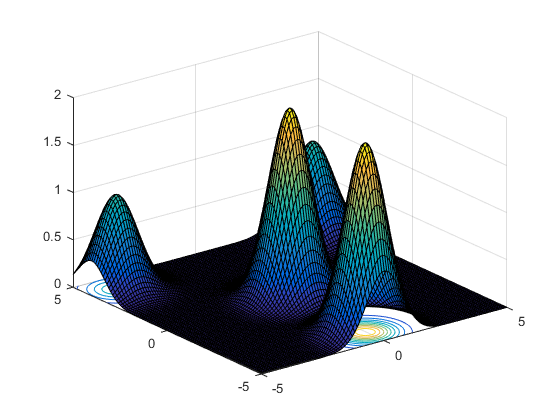
نحوه همگرایی الگوریتم کرم شب تاب به نقاط بیشینه (بهینه سراسری و محلی)، در شکل زیر نمایش داده شده است.

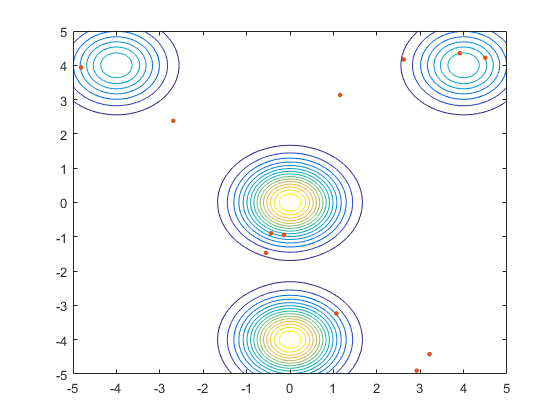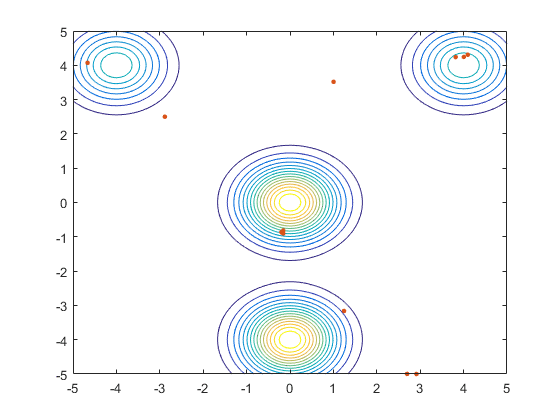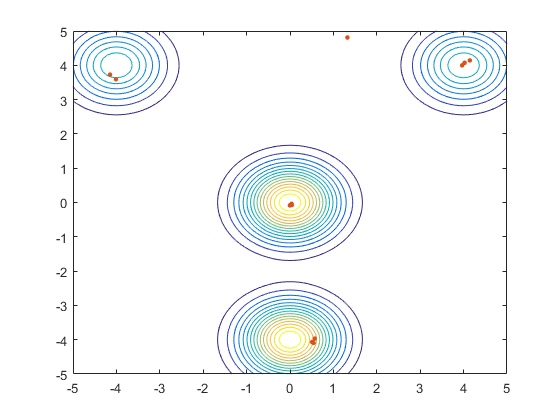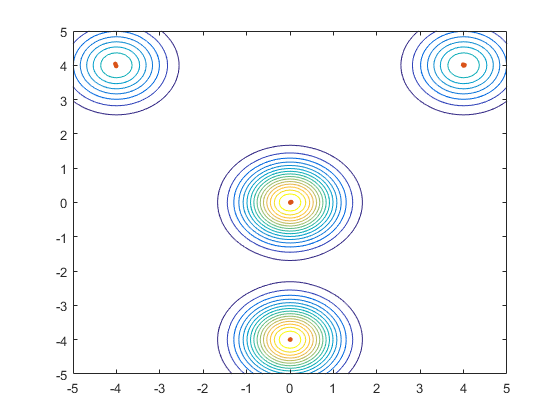
کدهای پیاده‌سازی الگوریتم کرم شب تاب برای حل مسائل بهینه‌سازی «نامقید» (Unconstrained) در ابعاد بالا

کدهای پیاده‌سازی الگوریتم کرم شب تاب برای حل مسائل بهینه‌سازی «غیرخطی» (Non-Linear) و «مقید» (Constrained) در ابعاد بالا

کدهای پیاده‌سازی الگوریتم کرم شب تاب برای حل مسائل بهینه‌سازی توسط گروه «یارپیز» (yarpiz)

در این نسخه از پیاده‌سازی الگوریتم کرم شب تاب در محیط متلب، تنظیمات زیر جهت بهینه‌سازی تابع De Jang، تابع Rosenbrock و تابع Ackley مورد استفاده قرار گرفته شده‌اند:

• حد بالا و پایین: به ترتیب مقدار 10 و مقدار 10-
• بیشینه تعداد تکرارهای لازم برای همگرایی به جواب بهینه: 1000 تکرار
• تعداد کرم‌های شب تاب موجود در جمعیت: 25 کرم شب تاب
• پارامتر $$\gamma$$ (پارامتر ضریب جذب): مقدار عددی 1
• مقدار پایه پارامتر جذابیت: مقدار عددی 2

کدهای لازم برای تعریف تابع De Jong در متلب

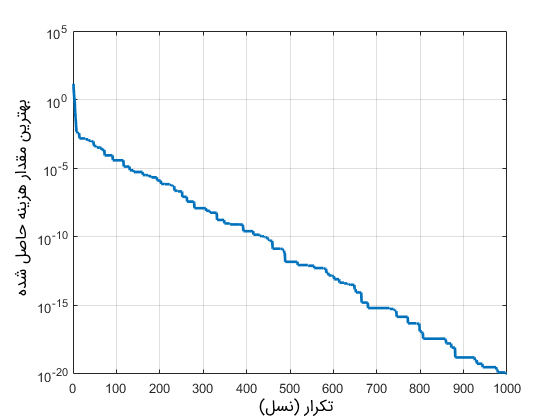
کدهای لازم برای تعریف تابع Rosenbrock در متلب

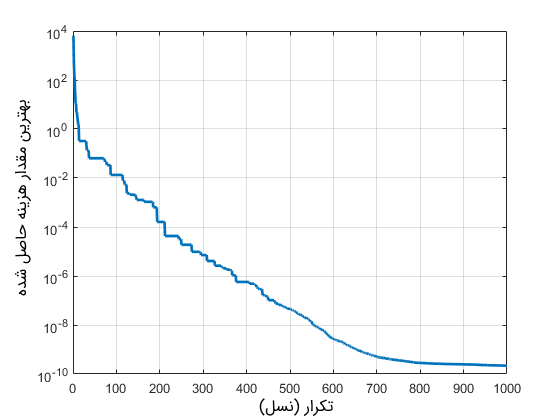
کدهای لازم برای تعریف تابع Ackley در متلب

جهت دسترسی به کدهای پیاده‌سازی تابع Ackley در متلب، روی لینک یا آیکون زیر کلیک کنید.

پیاده‌سازی الگوریتم کرم شب تاب در زبان جاوا

جهت دسترسی به کدهای پیاده‌سازی مؤلفه‌های مختلف الگوریتم کرم شب تاب در زبان جاوا، روی لینک یا آیکون زیر کلیک کنید.

پیاده‌سازی الگوریتم کرم شب تاب در زبان C++/C‎

جهت دسترسی به کدهای پیاده‌سازی مؤلفه‌های مختلف الگوریتم کرم شب تاب در زبان C++/C، روی لینک یا آیکون زیر کلیک کنید.

دوره ویدیویی آموزش الگوریتم کرم شب تاب یا Firefly Algorithm در متلب

در صورتی که به موضوع الگوریتم کرم شب تاب یا Firefly Algorithm علاقه‌مند هستید، می‌توانید دوره ویدیویی آموزش این الگوریتم و پیاده‌سازی آن در متلب را در وب سایت فرادرس مشاهده کنید. در این دوره آموزشی، ابتدا مروری بر مبانی تئوری الگوریتم کرم شب تاب انجام (Firefly Algorithm) شده است. سپس، پیاده سازی عملی این الگوریتم در محیط متلب، برای حل یک مساله بهینه سازی پیوسته، مورد بررسی قرار گرفته است. همچنین، برای آشنا کردن مخاطبان با نحوه پیاده‌سازی این الگوریتم بهینه‌سازی در محیط متلب، پیاده‌سازی گام به گام تمام مراحل الگوریتم کرم شب تاب (جهت همگرایی به جواب بهینه الگوریتم‌های تکاملی)، در محیط متلب مورد بررسی قرار گرفته‌ شده است. علاوه بر این، نسخه‌های تغییر یافته الگوریتم کرم شب تاب و ویژگی‌های مشخصه آن‌ها معرفی خواهد شد. مدرس این دوره آموزشی دکتر سید مصطفی کلامی هریس و مدت زمان دوره 1 ساعت و 12 دقیقه است.

جمع‌بندی

در این مطلب، نحوه فرمول‌بندی کردن الگوریتم کرم شب تاب ارائه شد. همچنین، شباهت‌ها و تفاوت‌های این الگوریتم با الگوریتم بهینه‌سازی ازدحام ذرات (PSO) مورد بررسی قرار گرفت. در مرحله بعد، نحوه پیاده‌سازی و مقایسه این الگوریتم با دیگر الگوریتم‌های مشابه نظیر الگوریتم ژنتیک (GA) و الگوریتم PSO شرح داده شد. نتایج ارزیابی و شبیه‌سازی الگوریتم‌های تکاملی در همگرایی به جواب بهینه سراسری توابع معیار مختلف نشان می‌دهد که الگوریتم PSO عملکرد به مراتب بهتری نسبت به الگوریتم‌های تکاملی مرسوم، نظیر الگوریتم ژنتیک، از خود نشان می‌دهد، با این حال، الگوریتم کرم شب تاب، نه تنها کارایی و عملکرد بهتری، در رسیدن به جواب بهینه توابع مختلف از خود نشان می‌دهد، بلکه نرخ موفقیت (Success Rate) بالاتری نسبت به الگوریتم ژنتیک و الگوریتم PSO دارد. نتایج ارائه شده، نشان دهنده این احتمال است که الگوریتم کرم شب تاب، الگوریتم قدرتمندی در حل مسائل بهینه‌سازی مختلف، حتی مسائل NP-Hard باشد.

الگوریتم کرم شب تاب استاندارد (پایه)، الگوریتم بسیار کارآمد و مؤثری در همگرایی به جواب بهینه توابع مختلف محسوب می‌شود. با این حال، در آزمایشات و شبیه‌سازی‌های انجام شده، بعضا مشاهده شده است که حتی با نزدیک شدن کرم‌های شب تاب به ناحیه حاوی جواب بهینه (همگرایی جمعیت به جواب بهینه)، تغییرات زیادی در جواب‌های تولید شده توسط الگوریتم (جهت حل مسأله بهینه‌‌سازی مورد نظر) مشاهده می‌‎شود. یک دلیل ممکن برای چنین پدیده‌ای، عامل تصادفی‌سازی در فرمول‌بندی الگوریتم کرم شب تاب است.

یک راه حل ممکن برای رفع چنین نقیصه‌ای و بهبود عملکرد الگوریتم کرم شب تاب و از همه مهم‌تر افزایش کیفیت جواب‌های تولید شده، کاهش تأثیر عامل تصادفی‌سازی به صورت تدریجی است. همچنین، با متغیر کردن پارامتر تصادفی‌سازی $$\alpha$$ و تدریجی کردن کاهش این پارامتر (هنگام نزدیک‌تر شدن هر چه بیشتر کرم‌های شب تاب به بهینه سراسری)، این امکان برای الگوریتم فراهم می‌شود تا بتواند همگرایی به بهینه سراسری را بهبود بخشیده و جواب‌های بهینه با کیفیتی تولید کند.

شایان توجه است که با ایجاد تغییرات اندکی در الگوریتم کرم شب تاب، می‌توان قابلیت حل کردن «توابع چندهدفه» (Multi-Objective Functions) را به این الگوریتم اضافه کرد. همچنین، ایجاد تغییرات مناسب در الگوریتم کرم شب تاب و استفاده از آن در مسائل «بهینه‌سازی ترکیبیاتی» (Combinatorial Optimization)، می‌تواند یکی از حوزه‌های ارتقاء الگوریتم کرم شب تاب قلمداد شود.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های الگوریتم‌‌های بهینه‌‌سازی هوشمند
• آموزش تئوری و عملی الگوریتم‌های ژنتیک
• مجموعه آموزش‌‌های الگوریتم‌های ژنتیک و محاسبات تکاملی
• الگوریتم بهینه سازی فاخته — از صفر تا صد
• الگوریتم ژنتیک — از صفر تا صد
• الگوریتم کلونی مورچگان — از صفر تا صد

^^