فرادرس
شبیه سازی مونت کارلو در پایتون — راهنمای کاربردی
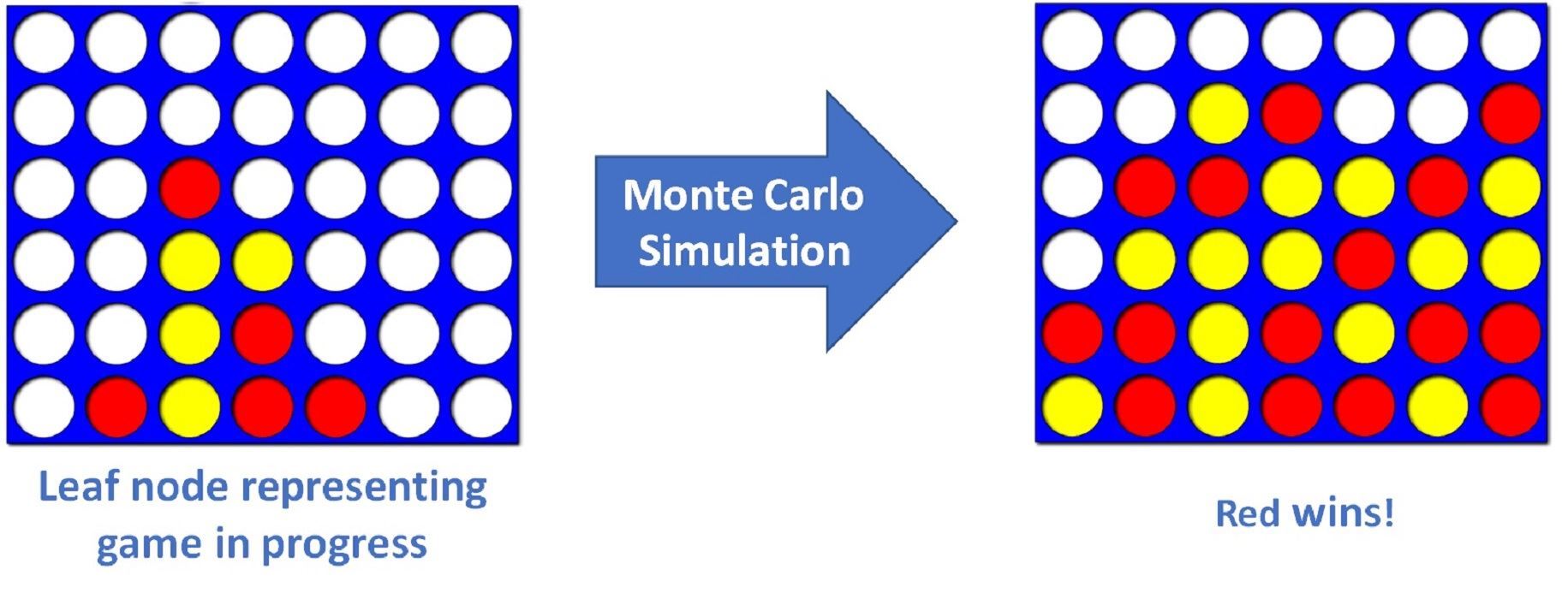
یکی از شیوه‌های شبیه‌سازی که برای حل بسیاری از مسائل بهینه‌سازی و محاسبه عددی انتگرال به کار می‌رود، «شبیه سازی مونت کارلو» (Monte Carlo Simulation) است. الگوریتم‌هایی که برمبنای این شیوه شبیه‌سازی پایه‌ریزی شده‌اند براساس نمونه‌گیری از توزیع‌های احتمال و آماری عمل می‌کنند. حیطه به کارگیری شبیه‌سازی مونت کارلو از حوزه محاسبات مالی تا تئوری‌های فیزیک گسترده است. برای مثال به منظور شبیه‌سازی اتفاقاتی که در یک رآکتور هسته‌ای رخ می‌دهد، می‌توان از شبیه‌سازی مونت‌کارلو استفاده کرد.
در این مطلب قصد داریم شیوه شبیه‌سازی مونت کارلو را معرفی کنیم. برای اجرای الگوریتم مربوطه نیز از زبان برنامه نویسی پایتون استفاده خواهیم کرد. به این منظور برای آشنایی با روش مونت کارلو بهتر است مطلب متد مونت‌کارلو – به زبان ساده و شبیه سازی مونت کارلو (Monte Carlo Simulation) – محاسبه انتگرال به روش عددی را مطالعه کنید. از طرفی اطلاع از شیوه‌های نمونه‌گیری که در نوشتار روش های نمونه‌گیری (Sampling) در آمار — به زبان ساده آمده است نیز خالی از لطف نیست. همچنین مطالعه مطلب توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس نیز به منظور آگاهی از توزیع‌ها آماری و کاربردشان توصیه می‌شود.
شبیه سازی مونت کارلو
همانطور که گفته شد یکی از کاربردهای شبیه‌سازی مونت‌کارلو، محاسبه انتگرال به صورت عددی است. برای مثال فرض کنید قرار است انتگرال زیر را محاسبه کنیم.
$$\large I= \int_0^{\infty} \dfrac{e^{-x}}{1+(x-1)^2}dx$$
رابطه ۱
همانطور که مشخص است این انتگرال را نمی‌توان به کمک روش‌های تحلیلی محاسبه کرد. بنابراین استفاده از روش‌های عددی در اینجا ضروری به نظر می‌رسد. از همین رو در ادامه به شیوه محاسبه تقریبی انتگرال به کمک شبیه‌سازی مونت‌کارلو می‌پردازیم.
محاسبه انتگرال به شیوه مونت‌کارلو
تکنیک مونت‌کارلو ساده (Crude Monte Carlo Simulation) یکی از ساده‌ترین تکنیک‌ها در گروه روش‌های شبیه‌سازی مونت‌کارلو است. البته نباید از این شیوه انتظار داشت که در انجام محاسبات دقت زیادی به خرج دهد. براساس قضیه مقدار میانگین مشخص است که برای تابع پیوسته و مشتق‌پذیر $$f$$ می‌توان رابطه زیر را نوشت:
$$\large f_{ave}=\dfrac{1}{b-a}\int_a^bf(x)dx$$
به این ترتیب به نظر می‌رسد که مقدار انتگرال را می‌توان به صورت ضرب میانگین مقدار انتگرال‌ده در فاصله بازه انتگرال محاسبه کرد.
$$\large f_{ave}\times (b-a) =\int_a^bf(x)dx$$
دقت کنید که در اینجا منظور از $$f_{ave}$$ همان میانگین مقدار انتگرال‌ده در بازه $$[a,b]$$است. تکنیک شبیه‌سازی مونت‌کارلو دقیقا بر همین اصل و قضیه مقدار میانگین عمل می‌کند. بنابراین به جای محاسبه انتگرال به صورت تحلیلی، از روش تقریبی به کمک میانگینگیری تابع انتگرال‌ده استفاده می‌کنیم. البته باید توجه داشت که در بعضی از موارد شیوه‌های انتگرال‌گیری عددی بوسیله روش‌های هندسی مانند روش نیوتن-رافسون نیز صورت می‌گیرد.
در شیوه محاسبه انتگرال با شبیه‌سازی مونت‌کارلو، مقادیری از مقدار متغیر ($$x$$) را براساس تولید اعداد تصادفی در بازه قابل تعریف برای انتگرال (در اینجا فاصله $$a$$ تا $$b$$) ایجاد می‌کنیم. برای مثال فرض کنید تابع $$f$$ به شکل ساده $$y=2x$$ باشد. بنابراین برای محاسبه انتگرال زیر در بازه $$[0,2]$$ چندین عدد تصادفی برای متغیر $$x$$ در فاصله $$[0,2]$$ ایجاد کرده و مقدار $$y=۲x$$ را محاسبه می‌کنیم. انتگرال موردنظر تقریباً برابر با میانگین مقدارهای $$y$$ خواهد بود.
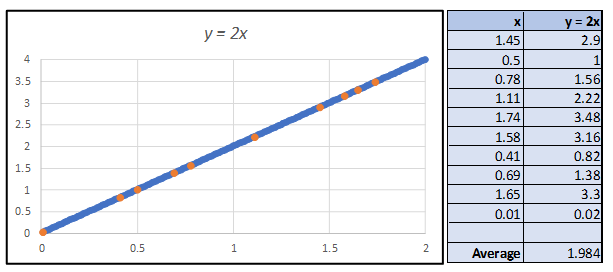
با توجه به تصویر بالا، مقدار انتگرال که توسط میانگین مقدارهای $$y$$ حاصل می‌شود برابر با $$1.984$$ است. در حقیقت می‌دانیم مقدار واقعی این انتگرال توسط رابطه زیر محاسبه می‌شود.
$$\large \int_0^2 2xdx= \dfrac{2x^2}{2}|^{2}_{0}=4-0=4$$
حال به مسئله اصلی بر می‌گردیم که محاسبه انتگرال رابطه ۱ بود. برای انجام محاسبات در این مرحله از کدهای پایتون استفاده می‌کنیم.
import numpy as np import math import random from matplotlib import pyplot as plt from IPython.display import clear_output e = 2.71828
همانطور که مشاهده می‌کنید ابتدا کتابخانه‌های مورد نیاز بارگذاری شده‌اند. از کتابخانه math برای تعریف تابع و از random نیز به منظور تولید نمونه تصادفی استفاده خواهیم کرد. همچنین از کتابخانه matplotlib نیز برای ایجاد و نمایش نمودارها استفاده می‌شود.
دستورات بعدی به منظور تولید اعداد تصادفی ایجاد شده‌اند. توجه داشته باشید که دو پارامتر min_value و max_value پارامترهای توزیع یکنواخت را مشخص کرده تا محدوده اعداد تصادفی تعیین شوند.
def get_rand_number(min_value, max_value):
"""
This function gets a random number from a uniform distribution between
the two input values [min_value, max_value] inclusively
Args:
- min_value (float)
- max_value (float)
Return:
- Random number between this range (float)
"""
range = max_value - min_value
choice = random.uniform(0,1)
return min_value + range*choice
در اینجا از توزیع احتمالی یکنواخت برای تولید اعداد تصادفی استفاده شد ولی ممکن است با توجه به شکل تغییرات تابع $$f(x)$$ از توزیع‌های دیگر آماری برای تولید اعداد تصادفی استفاده کرد که با تابع $$f(x)$$ شبیه‌تر باشند. این نکته را در بخش «اهمیت نمونه‌گیری» شرح خواهیم داد.
از طرفی برای تعریف تابع محاسباتی مورد نظر در انتگرال نیز از کد زیر استفاده کرده‌ایم. (f_of_x(x الگوی محاسباتی را برای انتگرال‌ده (Integrand)، مشخص می‌کند.
def f_of_x(x):
"""
This is the main function we want to integrate over.
Args:
- x (float) : input to function; must be in radians
Return:
- output of function f(x) (float)
"""
return (e**(-1*x))/(1+(x-1)**2)
اجرای شبیه‌سازی مونت کارلو
به منظور انجام شبیه‌سازی مونت کارلو برای محاسبه انتگرال بالا، باید مراحل زیر طی یک الگوریتم به اجرا درآیند.
- یک نمونه تصادفی از یک توزیع آماری (مثلا توزیع یکنواخت) در بازه انتگرال‌گیری تولید شود.
- انتگرال‌ده براساس مقدار حاصل از مرحله ۱ محاسبه شود.
- مراحل ۱ و ۲ به تعداد دلخواه (برای رسیدن به دقت مناسب) تکرار شوند.
- مقدارهای حاصل از مرحله ۳ میانگینگیری شده و مقدار این میانگین در فاصله بین کران‌های انتگرال ضرب شود.
def crude_monte_carlo(num_samples=10000):
"""
This function performs the Crude Monte Carlo for our
specific function f(x) on the range x=0 to x=5.
Notice that this bound is sufficient because f(x)
approaches 0 at around PI.
Args:
- num_samples (float) : number of samples
Return:
- Crude Monte Carlo estimation (float)
"""
lower_bound = 0
upper_bound = 5
sum_of_samples = 0
for i in range(num_samples):
x = get_rand_number(lower_bound, upper_bound)
sum_of_samples += f_of_x(x)
return (upper_bound - lower_bound) * float(sum_of_samples/num_samples)
کدی که در بالا قابل مشاهده است، تابعی است که بر اساس 10000 نمونه تصادفی (num_samples=10000) محاسبه انتگرال رابطه ۱ را در بازه ۰ تا ۵ انجام می‌دهد. مقدار حاصل از اجرای این کد برای انتگرال برابر است با $$0.6994$$.
محاسبه واریانس برآوردگر
سوالی که در این میان مطرح می‌شود، این است که چگونه می‌توان خطای محاسباتی را مشخص کرد. آیا افزایش تعداد نمونه‌های تصادفی (مثلا رساندن تعداد آن‌ها به ۱۰۰۰۰ مشاهده) دقت محاسبات را به شکل محسوسی تغییر می‌دهد. یا به طور دقیق‌تر می‌توان این سوال را مطرح کرد که چه رابطه‌ای بین تعداد نمونه‌ها و خطای حاصل از محاسبات وجود دارد.
از آنجایی که مقدار واقعی انتگرال مشخص نیست نمی‌توان به راحتی فاصله محاسباتی بین مقدار واقعی و مقدار تقریبی را مبنا قرار داده و خطای محاسبه انتگرال را تعیین کرد. در عوض می‌توانیم براساس نمونه‌های مختلف، محاسبات را انجام داده و خطای میانگین (واریانس میانگین نتایج) را مبنای اندازه خطا قرار دهیم. به این ترتیب واریانس یا میانگین مرابعات انحراف از میانگین را به عنوان خطا در نظر خواهیم گرفت.
$$\large \sigma^2 = E(I^2)-E^2(I)$$
همانطور که مشخص است رابطه بالا مربوط به شیوه محاسبه واریانس برای متغیر تصادفی $$I$$ است. از طرفی می‌دانیم که با تغییر نمونه‌ها و تکرار الگوریتم مقدار متفاوتی برای انتگرال بدست خواهد آمد. واریانس مقدارهای محاسبه شده برای انتگرال را بر مبنای دسته‌های نمونه‌های متفاوت، مبنای خطا در نظر می‌گیریم. به این ترتیب رابطه زیر را خواهیم داشت.
$$\large \sigma^2=[\dfrac{b-a}{N}\sum f^2(x_i)]-[\sum_{i=1}^N\dfrac{b-a}{N}f(x_i)]^2$$
کدی که در ادامه مشاهده می‌کنید به منظور محاسبه واریانس (خطای) شبیه‌سازی مونت‌کارلو نوشته شده است.
def get_crude_MC_variance(num_samples):
"""
This function returns the variance fo the Crude Monte Carlo.
Note that the inputed number of samples does not neccissarily
need to correspond to number of samples used in the Monte
Carlo Simulation.
Args:
- num_samples (int)
Return:
- Variance for Crude Monte Carlo approximation of f(x) (float)
"""
int_max = 5 # this is the max of our integration range
# get the average of squares
running_total = 0
for i in range(num_samples):
x = get_rand_number(0, int_max)
running_total += f_of_x(x)**2
sum_of_sqs = running_total*int_max / num_samples
# get square of average
running_total = 0
for i in range(num_samples):
x = get_rand_number(0, int_max)
running_total = f_of_x(x)
sq_ave = (int_max*running_total/num_samples)**2
return sum_of_sqs - sq_ave
براساس 10000 نقطه، مقدار واریانس براساس کد بالا برابر با $$0.266$$ است که می‌توان خطا را در این حالت به صورت زیر محاسبه کرد.
$$\large \operatorname{Error} =\left(\dfrac{\sigma^2}{N}\right)^{\tfrac{1}{2}}$$
پس مطابق با رابطه بالا میزان خطا برای محاسبه این انتگرال برابر با $$0.005$$ است. البته مقدار خطا زیاد به نظر نمی‌رسد و می‌توان به عنوان یک روش ساده و کارا، محاسبه به کمک تکنیک مونت‌کارلو را مد نظر قرار داد. برای افزایش میزان دقت برآورد باید تعداد نمونه‌ها را بیشتر کرد. ولی از طرفی افزایش تعداد نقاط، بار محاسباتی و زمان بیشتری برای اجرای الگوریتم را به همراه دارد. سوالی که در این قسمت مطرح می‌شود این است که چگونه می‌توانیم با هزینه زمانی کمتر و زمان کوتاه‌تر به پاسخ مناسب‌تر با خطای کمتری در محاسبه انتگرال به روش مونت‌کارلو رسید.
اهمیت نمونه‌گیری
یکی از روش‌های کاهش خطای در شبیه‌سازی مونت‌کارلو، استفاده از نمونه‌هایی است که از محاسبه مقدار انتگرال از اهمیت بیشتری برخوردار هستند. به این ترتیب نقاط با اهمیت در نمونه متمایز شده و از آن‌ها برای محاسبات انتگرال استفاده می‌شود. در نتیجه بدون آنکه تعداد نمونه‌ها افزایش یابد، می‌توان با دقت بیشتری عملیات شبیه‌سازی مونت‌کارلو را انجام داد.
اهمیت نمونه‌گیری را می‌توان به شکلی تاثیر نمونه‌گیری در محاسبه انتگرال در نظر گرفت. بنابراین به آن گاهی «نمونه‌گیری با اهمیت» نیز می‌گویند. انتخاب نقاطی که دارای اهمیت بیشتری هستند به توزیع داده‌ها بستگی دارد. برای مثال فرض کنید تابع پله‌ای $$f(x)$$ مطابق با تصویر زیر مورد نظر است. مشخص است که در فاصله $$[0,2]$$ این تابع مقداری برابر با ۱ داشته و در بعد از آن صفر است.
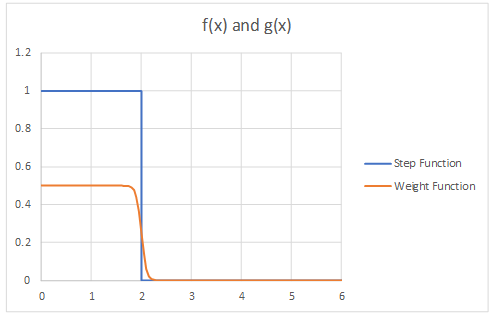
اگر در فاصله $$[0,6]$$ از ۱۰ نمونه تصادفی استفاده کنیم، مقدار تابع پله‌ای ممکن است به صورت زیر آید.
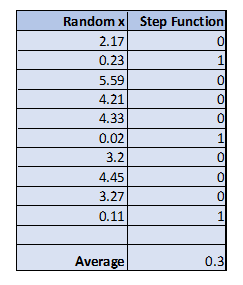
همانطور که می‌بینید میانگین مقادیر تابع برای چنین نقاطی برابر با $$0.3$$ است. به این ترتیب مقدار انتگرال تابع $$f(x)$$ در بازه $$[0,6]$$ برابر با $$1.8$$ خواهد بود. ولی اگر به جای استفاده از همه این نقاط، به نقاطی که $$x$$ آن‌ها بزرگتر از ۰ است، اهمیت بیشتری بدهیم، سرعت و نتیجه محاسبات دقیق‌تر نخواهد شد.
به منظور تعیین اهمیت برای نقاط می‌توان از تابع دیگری به نام $$g(x)$$ استفاده کنیم که وزن هر یک از مقدارهای تصادفی را در محاسبه انتگرال تعیین می‌کند. برای سادگی کار فرض کنید که این تابع هر یک از مقدارهای تابع $$f(x)$$ وزنی تقریبا برابر با $$\frac{1}{2}$$ می‌دهد. نمودار این تابع در تصویر تابع پله‌ای به رنگ نارنجی دیده می‌شود.
واضح است که در این حالت اثر نمونه‌ها در محاسبه انتگرال دیگر «نااریب» (Unbiased) نیست و به سمت مقادیری که دارای مقداری مخالف صفر هستند تمایل بیشتری دارد. ولی نکته جالب در اینجا آن است که نتیجه حاصل از انتگرال که بوسیله نقاط «اریب» (Basie) حاصل شده، نااریب خواهد بود.
حال نتیجه محاسبه میانگین تابع $$f(x)$$ را با ضریب یا وزن $$g(x)$$ در تصویر زیر مشاهده می‌کنید.
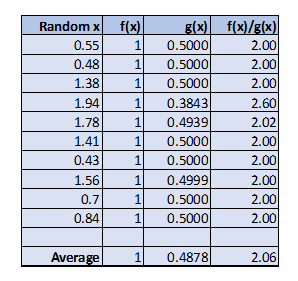
میانگین مقدارهای مربوط به حاصل‌ضرب $$f(x)$$ در $$g(x)$$ در سطر آخر دیده می‌شود. همانطور که می‌بینید این مقدار یعنی $$2.06$$ به مقدار واقعی انتگرال که برابر با $$2$$ است بسیار نزدیک‌تر از حالت قبل است. حال به دلیل و برهان ریاضی این مسئله خواهیم پرداخت.
منطق ریاضی در مسئله اهمیت نمونه‌گیری
فرض کنید که بین دو تابع $$f(x)$$ و $$g(x)$$ رابطه زیر برقرار است.
$$\large \dfrac{f(x)}{g(x)} \approx k$$
در این حالت به نظر می‌رسد که شرایط زیر باید برای تابع $$g(x)$$ فراهم آید.
- تابع $$g(x)$$ انتگرال‌پذیر باشد.
- تابع $$g(x)$$ روی بازه انتگرال‌گیری ($$a,b$$) نامنفی باشد.
- انتگرال نامعین $$g(x)$$ که از این به بعد با $$G(X)$$ نشان داده می‌شود، معکوس‌پذیر باشد.
- انتگرال تابع $$g(x)$$ روی بازه $$[a.b]$$ برابر با ۱ باشد.
نکته: اگر نسبت دو تابع $$f(x)$$ و $$g(x)$$ دقیقا برابر با $$k$$ باشد، با توجه به شرایط گفته شده، $$f(x)$$ نیز انتگرال‌پذیر بوده و احتیاجی به روش‌های عددی نیست و برای مثال با تقسیم نتیجه انتگرال تابع $$g(x)$$ در بازه مورد نظر، انتگرال $$f(x)$$ نیز به سادگی حاصل می‌شود.
با توجه به شرط انتگرال‌پذیری تابع $$g(x)$$ می‌توانیم رابطه زیر را بنویسیم. حاصل این انتگرال را با $$r=G(x)$$ نشان می‌دهیم.
$$\large r=G(x)=\int_0^x g(t)dt$$
با توجه به خصوصیات تابع $$g(x)$$ می‌دانیم که $$0\leq r \leq 1$$. این امر کمک می‌کند که هنگام تولید اعداد تصادفی، از توزیع یکنواخت در فاصله $$[0,1]$$ استفاده کنیم.
به این ترتیب برای محاسبه انتگرال از رابطه زیر کمک خواهیم گرفت. مشخص است که منظور از $$G^{-1}$$ معکوس تابع $$G$$ در نقطه $$r$$ است. همانطور که گفته شد یکی از شرایط تابع $$G$$، معکوس‌پذیری بود.
$$\large I =\dfrac{1}{N}\sum_{i=1}^N\dfrac{f(G^{-1}(r_i))}{g(G^{-1}(r_i))}$$
به این ترتیب با انتخاب نمونه‌های تصادفی با حجم $$N$$ از یک توزیع یکنواخت و نسبت دادن آن‌ها به $$r_i$$ مراحل کار آغاز می‌شود.
نکته: اگر $$g(x)$$ یک تابع چگالی احتمال باشد، آنگاه $$G(x)$$ نیز تابع توزیع آن را نشان می‌دهد. به این ترتیب $$G^{-1}$$ بیانگر چندک توزیع $$G$$ خواهد بود.
پیاده‌سازی مسئله اهمیت نمونه‌گیری در پایتون
دوباره به مسئله انتگرالی که در ابتدای متن به آن اشاره کردیم، باز می‌گردیم. برای انتخاب تابع $$g(x)$$ مناسب برای انتگرال بهتر است نمودار مربوط به انتگرال‌ده را ترسیم کنیم.
کدی که در ادامه مشاهده می‌کنید، نمودار تابع مربوط به انتگرال‌ده یا همان $$f(x)$$ را در بازه ۰ تا ۶ ترسیم می‌کند.
xs = [float(i/50) for i in range(int(300))]
ys = [f_of_x(x) for x in xs]
plt.plot(xs,ys)
plt.title("f(x)");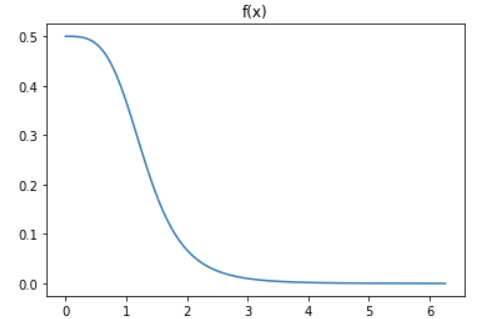
همانطور که در نمودار دیده می‌شود، برای مقادیر بزرگتر از حدود ۳ تا بی‌نهایت، مقدار تابع $$f(x)$$به صفر بسیار نزدیک است. بنابراین بهتر است نقش این مقادیر را در محاسبات مربوط به شبیه‌سازی مونت‌کارلو کمرنگ‌تر کنیم.
به نظر می‌رسد انتخاب تابعی به شکل زیر می‌تواند این وظیفه را به خوبی انجام دهد.
$$\large g(x)=A\exp({-\lambda x})$$
به منظور تعیین پارامترهای $$A$$ و $$\lambda$$ باید از شرایط مربوط به تابع $$g(x)$$ کمک گرفت. یکی از شرایط مهم در انتخاب مناسب این تابع، به صورت زیر نوشته می‌شود.
$$\large 1 = \int_0^{\infty}g(x)dx\rightarrow A=\lambda$$
بنابراین اگر بتوانیم پارامتر $$\lambda$$ را به درستی برآورد کنیم، تابع $$g(x)$$ را هم به شکل مناسب خواهیم داشت. برای پیدا کردن این پارامتر از واریانس استفاده می‌کنیم. به این ترتیب مقدار $$\lambda$$ را به شکلی تعیین می‌کنیم که واریانس برآورد انتگرال کمترین مقدار باشد. در این حالت واریانس مقدار انتگرال به صورت زیر محاسبه می‌شود.
$$\large \sigma^2=[\dfrac{1}{N}\sum_i^N\dfrac{f^2(x_i)}{g^2(x_i)}]-[\sum_i^N\dfrac{1}{N}\dfrac{f(x_i)}{g(x_i)}]^2$$
به این ترتیب مقدار $$\lambda$$ را در بازه $$[0.05,3.0]$$ با گام‌هایی برابر با $$0.5$$ تغییر می‌دهیم و کمترین واریانس را پیدا می‌کنیم. با این کار برآورد مناسبی برای $$\lambda$$ حاصل می‌شود.
الگوریتم زیر به این منظور تهیه شده است.
- مقدار $$\lambda=0.05$$
- محاسبه واریانس انتگرال
- افزایش مقدار $$\lambda$$ به میزان $$0.5$$ واحد
- تکرار گام‌های ۲ و ۳ تا $$\lambda>3$$ شود.
- انتخاب کوچکترین واریانس و مقدار $$\lambda$$ متناظر آن
- محاسبه انتگرال براساس $$A$$ و $$\lambda$$ محاسبه شده.
کدهای زیر به منظور اجرایی کردن این الگوریتم تهیه شده‌اند.
# this is the template of our weight function g(x)
def g_of_x(x, A, lamda):
e = 2.71828
return A*math.pow(e, -1*lamda*x)
def inverse_G_of_r(r, lamda):
return (-1 * math.log(float(r)))/lamda
def get_IS_variance(lamda, num_samples):
"""
This function calculates the variance if a Monte Carlo
using importance sampling.
Args:
- lamda (float) : lamdba value of g(x) being tested
Return:
- Variance
"""
A = lamda
int_max = 5
# get sum of squares
running_total = 0
for i in range(num_samples):
x = get_rand_number(0, int_max)
running_total += (f_of_x(x)/g_of_x(x, A, lamda))**2
sum_of_sqs = running_total / num_samples
# get squared average
running_total = 0
for i in range(num_samples):
x = get_rand_number(0, int_max)
running_total += f_of_x(x)/g_of_x(x, A, lamda)
sq_ave = (running_total/num_samples)**2
return sum_of_sqs - sq_ave
# get variance as a function of lambda by testing many
# different lambdas
test_lamdas = [i*0.05 for i in range(1, 61)]
variances = []
for i, lamda in enumerate(test_lamdas):
print(f"lambda {i+1}/{len(test_lamdas)}: {lamda}")
A = lamda
variances.append(get_IS_variance(lamda, 10000))
clear_output(wait=True)
optimal_lamda = test_lamdas[np.argmin(np.asarray(variances))]
IS_variance = variances[np.argmin(np.asarray(variances))]
print(f"Optimal Lambda: {optimal_lamda}")
print(f"Optimal Variance: {IS_variance}")
print(f"Error: {(IS_variance/10000)**0.5}")
با اجرای این کد مشخص است که مقدار $$\lambda=1.65$$ با استفاده از ۱۰ هزار نمونه حاصل می‌شود. نمودار مقایسه تابع $$f(x)$$ و $$g(x)$$ حاصل از برنامه بالا در ادامه دیده می‌شود.
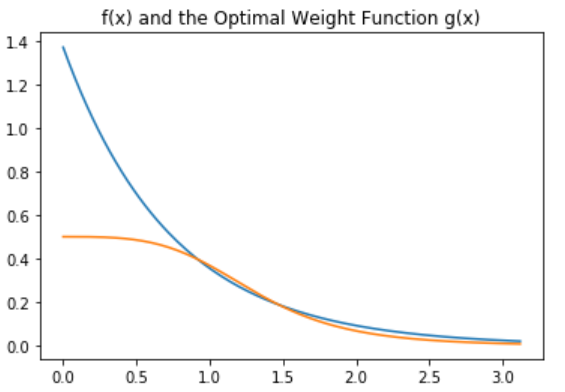
واریانس انتگرال محاسبه شده براین اساس نیز $$\sigma^2=0.0465$$ خواهد بود پس می‌توان گفت که خطای برآورد انتگرال تقریبا برابر با $$error=0.0022$$ است. به این ترتیب به نظر می‌رسد که استفاده از نمونه‌های با اهمیت باعث شده است که خطای انتگرال‌گیری به نصف حالت قبل، تقلیل یابد.
حال با استفاده از کد زیر به کمک تابع $$g(x)$$ ساخته شده انتگرال را محاسبه خواهیم کرد.
def importance_sampling_MC(lamda, num_samples):
A = lamda
running_total = 0
for i in range(num_samples):
r = get_rand_number(0,1)
running_total += f_of_x(inverse_G_of_r(r, lamda=lamda))/g_of_x(inverse_G_of_r(r, lamda=lamda), A, lamda)
approximation = float(running_total/num_samples)
return approximation
# run simulation
num_samples = 10000
approx = importance_sampling_MC(optimal_lamda, num_samples)
variance = get_IS_variance(optimal_lamda, num_samples)
error = (variance/num_samples)**0.5
# display results
print(f"Importance Sampling Approximation: {approx}")
print(f"Variance: {variance}")
print(f"Error: {error}")
با اجرای این کد، مقدار برآورد شده برای انتگرال برابر با $$0.6983$$ خواهد شد. به نظر می‌رسد که بهبودی نسبی در مقدار انتگرال حاصل شده. نکته قابل توجه این است که این میزان بهبود بدون استفاده از نقاط بیشتر بدست آمده است و صرفا با استفاده از تابع وزنی $$g(x)$$ ایجاد شده است.
خلاصه
در این مطلب با روش شبیه‌سازی مونت‌کارلو و شیوه محاسبه انتگرال به کمک آن آشنا شدیم. همچنین به منظور بهبود نتایج انتگرال‌گیری، از نقاط با اهمیت بوسیله تکنیک اهمیت نمونه‌گیری استفاده کردیم.
اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
- مجموعه آموزش‌های نرم‌افزارهای آماری
- آموزش محاسبه انتگرال به کمک شبیه سازی مونت کارلو
- شبیه سازی سیستم با سیمیولینک
- آموزش آمار و احتمال مهندسی
- آزمایش تصادفی، پیشامد و تابع احتمال
- توزیع یکنواخت گسسته و پیوسته — مفاهیم و کاربردها
- شبیه سازی مونت کارلو (Monte Carlo Simulation) – محاسبه انتگرال به روش عددی
^^
