امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها

در تئوری آمار و احتمال، «متغیر تصادفی» (Random Variable) و تابع توزیع آن بسیار به کار می‌رود. هر چند که بسیاری از ویژگی‌ها و خصوصیات متغیر تصادفی بوسیله تابع توزیع آن مشخص می‌شوند ولی به عنوان شاخصی که قابلیت مقایسه بین مقدارهای متغیرهای تصادفی مختلف را داشته باشد، احتیاج به معیاری ساده‌تر از تابع توزیع احتمال داریم. بنابراین اگر «تابع توزیع احتمال» (Probability Distribution Function) برای متغیر تصادفی همان نقش «جدول فراوانی» (Frequency Table) برای داده‌ها را داشته باشد، نیاز است مانند میانگین که اطلاعات جدول فراوانی را خلاصه می‌کند از شاخص یا معیاری برای خلاصه کردن اطلاعات تابع توزیع احتمال کمک گرفت. این شاخص می‌تواند «امید ریاضی» (Expectation Value) باشد که گاهی به آن «مقدار مورد انتظار» (Expected Value) نیز می‌گویند. در این مطلب امید ریاضی و خصوصیات آن معرفی و کاربرد آن را در محاسبه شاخص‌های دیگر مانند واریانس، کوواریانس و ضریب همبستگی، بررسی می‌کنیم. در انتها نیز به چند قضیه مهم در رابطه با امید ریاضی که از اهمیت بیشتری برخوردارند، اشاره خواهیم کرد.

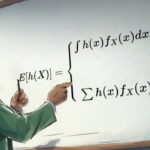
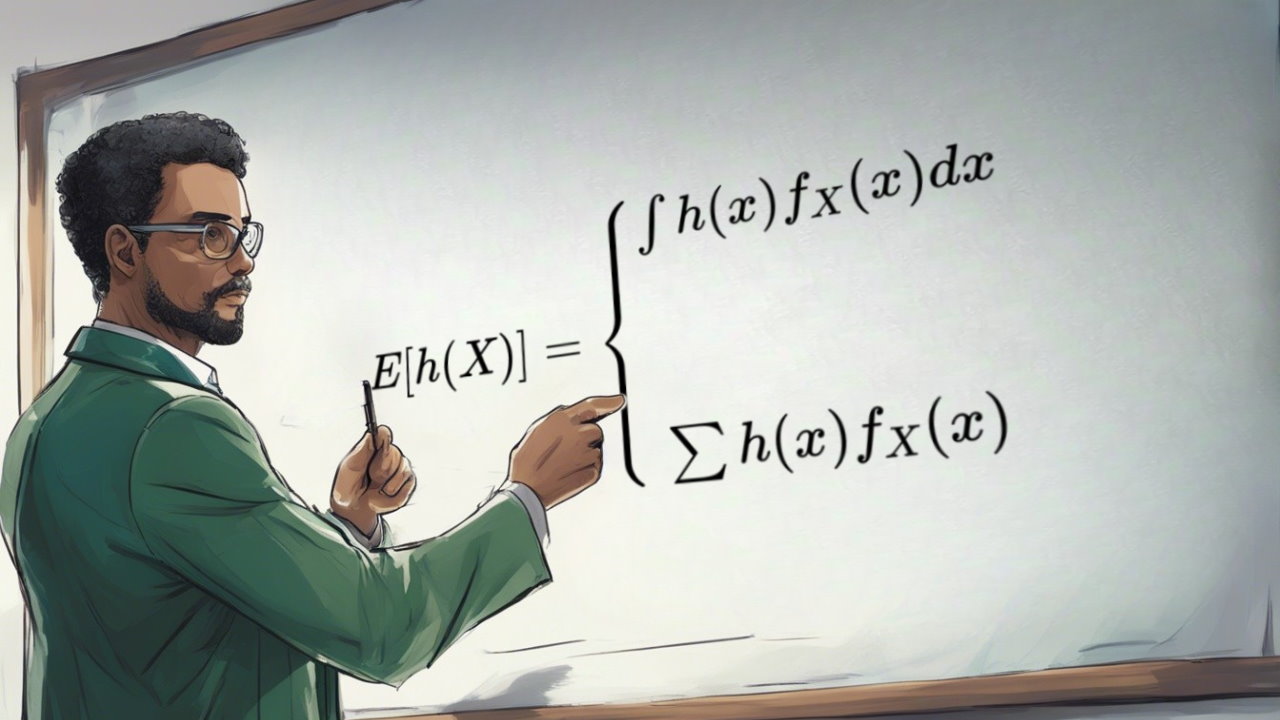
برای استفاده بیشتر از این مطلب بهتر است ابتدا مطلب‌های متغیر تصادفی، تابع احتمال و تابع توزیع احتمال، آزمایش تصادفی، پیشامد و تابع احتمال و میانگین وزنی — به زبان ساده را مطالعه کرده باشید.

امید ریاضی

ایده اصلی مطرح شده در مورد امید ریاضی به سال‌های دور بر می‌گردد. زمانی که «بلز پاسکال» (Blaise Pascal) دانشمند و ریاضیدان فرانسوی در سال ۱۶۵۴ به مسئله‌ای با موضوع بازی‌های شانسی برخورد کرد. او می‌خواست متوسط درآمد فردی که در چنین بازی شرکت می‌کند را محاسبه کرده و مشخص کند در صورتی که فرد در تعداد زیادی از این بازی شرکت کند آیا سود نصیبش خواهد شد و یا زیان هنگفتی خواهد کرد. او همچنین به میزان دارایی که بازیکن در هر مرحله صرف کرده توجه داشت و آن را به عنوان پارامتری در حل این مسئله در نظر گرفت.

فیلم آموزش تئوری احتمالات – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

از آنجایی که بازی به صورت شانسی برنده یا بازنده را مشخص می‌کند، او اجبار به دخیل کردن احتمال در چنین محاسباتی داشت در نتیجه با همکار خود «پیر دو فرما» (Pierre de Fermat) دیگر دانشمند فرانسوی در این زمینه مشورت کرد و هر یک با دو شیوه مختلف به نتیجه یکسانی رسیدند. آن‌ها یافته خود را منتشر نکردند و نامی نیز برای نتیجه محاسبات خود انتخاب نکردند.

سال‌ها بعد «پیر لاپلاس» (Pierre Laplace) در ۱۸۱۴ طی مقاله‌ای به مفهوم کامل و روشنی از امید ریاضی پرداخت. همچنین انتخاب علامت برای این شاخص که به صورت حرف E نمایش داده می‌شود نیز از ابتکارات «ویتورت» (Whitworth) ریاضیدان انگلیسی است. حال بهتر است که برای درک مفهوم امید ریاضی به بررسی یک مثال بپردازیم.

مثال ۱

فرض کنید فردی در یک بازی شانسی شرکت کرده است؛ احتمال برد او 0٫2 است و در نتیجه احتمال اینکه ببازد نیز برابر با 0٫8 است. همچنین فرض کنید که در صورت برنده شدن به وی مقدار ۱۰۰ تومان داده می‌شود. ضمناً اگر بازی را ببازد، باید مبلغ ۱۰ تومان جریمه پرداخت کند. به نظر شما او در این بازی نفع خواهد برد یا ضرر خواهد کرد؟

برای پاسخ به این سوال باید متوسط دریافت یا پرداخت‌های او را محاسبه کنیم. این کار را به واسطه محاسبات زیر انجام می‌دهیم. از آنجایی که 0٫2 احتمال دارد که 100 تومان برنده شود، به نظر می‌رسد اگر وارد بازی شود 0٫2×100=۲۰ تومان درآمد خواهد داشت. از طرفی در چنین وضعیتی نیز ممکن است 0٫8×10=8 تومان جریمه شود. بنابراین به طور متوسط در هر بار بازی، احتمال دارد 12 تومان درآمد کسب کند.

$$0.2\times 100-0.8\times 10=12$$

حال فرض کنید که X متغیر تصادفی باشد که مقدار a را به عنوان مبلغ جایزه و (b-) را به عنوان جریمه دریافت می‌کند. احتمال کسب جایزه برابر با p و احتمال جریمه نیز برابر با $$1-p$$ است. در نتیجه مقدار متوسط به صورت زیر محاسبه می‌شود:

$$a\times p +(-b)\times (1-p)$$

بنابراین اگر X را با تکیه‌گاه $$S=\{x_1,x_2,\ldots,x_n\}$$ در نظر بگیریم و احتمال مشاهده هر یک از مقدارهای تکیه‌گاه نیز توسط تابع احتمال p معرفی شده باشد،‌ متوسط مقدار متغیر تصادفی X‌ که آن را با $$E(X)$$‌ نشان می‌دهیم برابر خواهد بود با:‌

$$E(X)=\large \sum_{i=1}^n p_ix_i$$

مثال ۲

فرض کنید X یک متغیر تصادفی با تابع احتمال $$p(X=x)$$ به صورت زیر باشد. آنگاه میانگین این متغیر تصادفی براساس تکیه‌گاهش، همان میانگین وزنی براساس وزنی‌هایی است که احتمال رخداد هر مقدار را نشان می‌دهند.

همانطور که دیده می‌شود، احتمال مشاهده مقدار ۱ بیشتر از بقیه است، پس اهمیت بیشتری در محاسبه میانگین خواهد داشت. از طرف دیگر مقدار ۴ نیز با احتمال کمتری رخ داده،‌ پس باید اهمیت کمتری در محاسبه میانگین داشته باشد. با توجه به تعریف میانگین وزنی، می‌توان اهمیت حضور هر یک از مقدارها را همان احتمال رخداد هر یک از آن‌ها، در نظر گرفت. باید توجه داشت که مقدار فراوانی درصدی، همان نقش احتمال را در جدول فراوانی دارد.

بنابراین مقدار مورد انتظار برای X به صورت زیر قابل محاسبه است:

$$1 \times \frac{1}{3}+2\times \frac{1}{4}+3\times \frac{1}{4}+4\times \frac{1}{6}=\frac{8+2\times 6+3\times 6+4\times 4}{24}=\frac{9}{4}=2.25$$

به این ترتیب انتظار داریم اگر چندین بار مقدارهایی از متغیر تصادفی X را مشاهده کنیم، متوسط آن‌ها برابر با 2٫25 باشد.

تعریف امید ریاضی متغیر تصادفی گسسته X

اگر X یک متغیر تصادفی گسسته با تکیه‌گاه S باشد، آنگاه امید ریاضی آن به صورت زیر تعریف می‌شود:

$$E(X)=\sum_{x\in S}x  P(X=x)$$

به این ترتیب می‌توان برای مثال امید ریاضی متغیر تصادفی برنولی را محاسبه کرد.

$$X\sim B(1,p)\rightarrow E(X)=1 \times p+0\times (1-p)=p$$

همچنین برای متغیر تصادفی هندسی نیز محاسبات مربوط به امید ریاضی در زیر دیده می‌شود:

$$X\sim G(p)\rightarrow E(X)= \sum_{x=1}^\infty xp(1-p)^{x-1}=p\sum_{x=1}^\infty x(1-p)^{x-1}=\dfrac{p}{(1-(1-p))^2}=\frac{1}{p}$$

تعریف امید ریاضی متغیر تصادفی پیوسته X

اگر X یک متغیر تصادفی پیوسته با تکیه‌گاه $$S=(a,b)$$ و تابع چگالی احتمال $$\displaystyle f_X(x)$$ باشد، آنگاه امید ریاضی آن به صورت زیر تعریف می‌شود:

$$E(X)=\large \int_{a}^{b}x f_X(x)dx$$

به این ترتیب می‌توان امید ریاضی متغیر تصادفی نرمال را به صورت زیر نوشت.

$$X\sim N(\mu,\sigma^2)\rightarrow E(X)=\displaystyle \int_{-\infty}^{\infty}x \frac{1}{\large\sqrt{2\pi\sigma^2}} e^{\dfrac{-1}{2\sigma^2}\large(x-\mu)^2}dx=\large \mu$$

خواص امید ریاضی

در ادامه به بررسی خصوصیات اولیه برای امید ریاضی می‌پردازیم. این خصوصیات در توسعه مفهوم امید ریاضی متغیر تصادفی نقش مهمی دارند.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

با توجه به مفهوم «متغیر تصادفی تباهیده» (Degenerate Random Variable) می‌توان نشان داد امید ریاضی برای هر مقدار ثابت برابر است با خود آن مقدار. در این حالت تابع احتمال برای چنین متغیر تصادفی برابر است با:

$$P(X=a)=1$$

بنابراین می‌توان نوشت:

$$E(X)=X P(X=a) =a$$

همچنین می‌توان انتظار داشت که اگر تکیه‌گاه متغیر تصادفی X‌ نامنفی باشد، امید ریاضی آن نیز مقداری نامنفی بدست آید. یعنی اگر $$X\geq 0$$ آنگاه $$E(X)\geq0$$.

حال فرض کنید $$X_1,X_2,\ldots,X_n$$ متغیرهای تصادفی باشند. آنگاه برای امید ریاضی مجموع این متغیرهای تصادفی می‌توان رابطه زیر را نوشت:

$$E(\sum_{i=1}^n X_i)=E(X_1+X_2+\ldots+X_n)=E(X_1)+E(X_2)+\ldots+E(X_n)=\sum_{i=1}^nE(X_i)$$

از طرفی اگر این متغیرهای تصادفی، هم توزیع نیز باشند به رابطه زیر خواهیم رسید.

$$E(\sum_{i=1}^n X_i)=E(X_1+X_2+\ldots+X_n)=nE(X_1)$$

به این ترتیب برای متغیر تصادفی توزیع دو جمله‌ای که از جمع متغیرهای تصادفی هم‌توزیع برنولی ساخته می‌شود، می‌توان نشان داد که امید ریاضی برابر با $$E(X)=np$$ است. البته، امید ریاضی برای مجموع متغیرهای تصادفی نرمال با میانگین $$\mu_i$$ برابر است با $$\mu=\sum \mu_i$$ زیرا متغیرهای تصادفی یاد شده، هم‌توزیع نیستند.

به طور کلی می‌توان برای ترکیب خطی از متغیرهای تصادفی، رابطه زیر را در نظر گرفت.

$$E(\sum_{i=1}^n a_i X_i)=E(a_1 X_1+ a_2 X_2+\ldots+a_n X_n)=a_1E(X_1)+a_2E(X_2)+\ldots+a_nE(X_n)$$

یکی از خصوصیات جالب امید ریاضی یکنوا بودن آن است. دو متغیر تصادفی X و Y با شرط $$X\leq Y$$ را در نظر بگیرید. می‌خواهیم نشان دهیم که $$E(X)\leq E(Y)$$. به این ترتیب اگر Z متغیر تصادفی باشد که از تفاضل بین X و Y حاصل شده است، مشخص است که مقدارهای آن همیشه منفی خواهد بود. در نتیجه امید ریاضی برای چنین متغیری نیز منفی بدست می‌آید. بنابراین خواهیم داشت:

$$E(Z)=E(X-Y)=E(X)-E(Y)\leq 0\rightarrow E(X)\leq E(Y)$$

همچنین اگر X و Y دو متغیر تصادفی مستقل باشند می‌توان رابطه زیر را برایشان برحسب امید ریاضی نوشت:

$$E(XY)=E(X)E(Y)$$

این تساوی نشان می‌دهد که در صورت استقلال، متوسط حاصلضرب دو متغیر تصادفی برابر با حاصلضرب متوسط آن‌ها است. از عکس این حالت زمانی که متغیرهای تصادفی X و Y دارای توزیع نرمال و همچنین حاصلضرب آن‌ها نیز دارای توزیع توام نرمال دو متغیره باشد، می‌توان مستقل بودن را نتیجه گرفت. به این معنی که با توجه به شرایط گفته شده اگر امید ریاضی حاصلضرب آن‌ها برابر با حاصلضرب امیدهایشان باشد می‌توان استقلال متغیر X و Y‌ را استنباط کرد.

اگر متغیر تصادفی X دارای تکیه‌گاهی نامنفی باشد، می‌توان با توجه به تعریف امید ریاضی،‌ رابطه‌ای بین آن و تابع توزیع احتمال نوشت. فرض کنید $$F(X)$$ تابع توزیع متغیر تصادفی X و $$E(X)$$ نیز امید ریاضی آن باشد. در نتیجه می‌توان رابطه زیر را بین این دو برای حالت گسسته و پیوسته اثبات کرد:

$$E(X)=\sum_{i=1}^\infty P(X\geq i)$$

$$E(X)=\int_{X\geq 0}(1-F_X(x))dx$$

قانون (ضعیف و قوی) اعداد بزرگ

قانون اعداد بزرگ از مهمترین قضایای مطرح شده در تئوری آمار و احتمال است. این قانون با توجه به مفهوم امید ریاضی تعریف شده است. قانون اعداد بزرگ بیان می‌کند که میانگین متغیرهای تصادفی هم توزیع و مستقل به سمت امید ریاضی آن‌ها میل می‌کند. فرض کنید $$X_1,X_2,\ldots$$ دنباله‌ای از متغیرهای تصادفی هم توزیع و مستقل با امید ریاضی برابر با $$\mu$$ باشند. آنگاه امید ریاضی میانگین آن‌ها زمانی که تعدادشان زیاد باشد، با امید ریاضی هر یک از آن‌ها برابر است. این موضوع در رابطه زیر مشخص شده است:

$$E(\dfrac{X_1+X_2+\ldots+X_n}{n})=\mu,\;\;\;as\; n\to \infty$$

این قانون آخرین بار توسط «الکساندر کینچین» (Aleksandr Khinchin) دانشمند آمار اهل روسیه در سال 1929 برای هر متغیر تصادفی دلخواه اثبات شد. البته ممکن است با دو شیوه از این قانون مواجه شده باشید. «قانون ضعیف اعداد بزرگ» (Weak Law of Large Numbers) و «قانون قوی اعداد بزرگ» (Stronge Law of Large Numbers). قانون اول و دوم هر دو یک چیز را مشخص می‌کنند ولی فضایی که در آن حد گرفته می‌شود متفاوت است. این قوانین هر چند دو عنوان مختلف دارند ولی مفهوم اصلی آن‌ها این است که با افزایش تعداد نمونه دقت برآورد میانگین جامعه افزایش می‌یابد.

 واریانس متغیر تصادفی

می‌دانیم که واریانس برای داده‌ها به معنی میانگین مربعات فاصله مقدارها از میانگینشان است. همین تعریف را نیز می‌توان در مفهوم متغیر تصادفی تعمیم داد.

فیلم آموزش آمار و احتمال مهندسی – حل تمرین و تست کنکور ارشد در فرادرس

کلیک کنید

بنابراین اگر میانگین را با تعریف امید ریاضی جایگزین کنیم،‌ شیوه محاسبه واریانس برای متغیر تصادفی X‌ مشخص می‌شود.

$$Var(X)=E(X-E(X))^2$$

در صورتی که این رابطه را بسط دهید و عمل توان رساندن را به انجام برسانید، خواهید دید که رابطه ساده‌تری برای محاسبه واریانس بدست خواهد آمد که کار محاسبات را آسان‌تر می‌کند.

$$Var(X)=E(X^2)-E^2(X)$$

این تساوی نشان می‌‌دهد که برای محاسبه واریانس متغیر تصادفی X کافی است تفاضل امید ریاضی مربعات X‌ را از مربع امید ریاضی X بدست آورد. ولی چگونه امید ریاضی را برای $$X^2$$ محاسبه کنیم. راه حل مشخص آن است که براساس تابع احتمال متغیر تصادفی X، تابع احتمال متغیر تصادفی $$X^2$$ را بدست آورده و سپس برحسب تعریف امید ریاضی عمل کنیم. ولی قضیه زیر در انجام این محاسبه به ما یاری می‌رساند و عملیات را بسیار ساده‌تر می‌کند.

قضیه امید ریاضی برای تابعی از متغیر تصادفی

اگر X یک متغیر تصادفی و $$g(X)$$ نیز تابعی از X باشد که امید ریاضی آن موجود است، آنگاه می‌توان $$E(g(X))$$‌ را به صورت زیر در دو حالت گسسته و پیوسته نوشت:

$$E(g(X))=\sum_{x\in S} g(x)P(X=x)$$

$$E(g(X))=\int_{x\in S} g(x)P(X=x)$$

بنابراین با استفاده از این قضیه به راحتی محاسبه $$E(X^2)$$ و در نتیجه واریانس متغیر تصادفی امکان‌پذیر است. همچنین به کمک این قضیه می‌توان نشان داد که امید ریاضی ترکیب خطی از یک متغیر تصادفی برابر با همان ترکیب خطی از امید ریاضی آن است.

$$E(aX+b)=aE(X)+b$$

کوواریانس دو متغیر تصادفی

بر طبق تعریف امید ریاضی متغیر تصادفی، کوواریانس بین دو متغیر تصادفی مثلا X و Y که به صورت $$Cov(X,Y)$$ نوشته می‌شود به شکل زیر قابل محاسبه است.

$$Cov(X,Y)=E(XY)-E(X)E(Y)$$

این مقدار میزان وابستگی بین دو متغیر تصادفی را نشان می‌دهد. چنانچه جهت تغییرات دو متغیر عکس یکدیگر باشند، مقدار آن منفی و اگر تغییرات در یک جهت باشند، مقدار کوواریانس مثبت خواهد شد. از نظر مقایسه وابستگی بین X و Y نسبت به X و W، اگر قدر مطلق $$Cov(X,Y)$$ بزرگتر از قدرمطلق $$Cov(X,W)$$ باشد رای به وابستگی بیشتر بین X و Y می‌دهیم.

نامساوی کوشی-شوارتز (Cauchy–Schwarz Inequality)

اگر X و Y‌ دو متغیر تصادفی باشند، آنگاه نامساوی زیر در موردشان صدق می‌کند.

$$Cov^2(X,Y)\leq Var(X)Var(Y)$$

این نامساوی اولین بار توسط «آگوستین کوشی» (Augustin Cauchy) دانشمند و ریاضیدان فرانسوی در سال 1821 معرفی گردید و به عنوان ابزاری موثر در بیشتر شاخه‌های ریاضی به کار گرفته شد.

در اینجا این نامساوی کمک می‌کند برای کوواریانس دو متغیر تصادفی، یک کران بالا در نظر گرفته شود. به این ترتیب می‌توان برای «ضریب همبستگی» (Correlation) نیز کران‌هایی در نظر گرفت. می‌دانیم ضریب همبستگی توسط رابطه‌ زیر قابل محاسبه است.

$$\large \rho(X,Y)=\dfrac{Cov(X,Y)}{[Var(X)Var(Y)]^\frac{1}{2}}$$

در نتیجه با توجه به نامساوی کوشی-شوارتز، کران‌های کوواریانس توسط رابطه زیر بدست می‌آیند:

$$-(Var(X)Var(Y))^\frac{1}{2}\leq Cov(X,Y)\leq (Var(X)Var(Y))^\frac{1}{2}$$

که با در نظر گرفتن این کران‌ها در رابطه بالا خواهیم داشت:

$$-1\leq\dfrac{Cov(X,Y)}{[Var(X)Var(Y)]^\frac{1}{2}}\leq 1$$

از همین رو برای سنجش بزرگی وابستگی بین دو متغیر بدون در نظر گرفتن واحد اندازه‌گیری آن‌ها از ضریب همبستگی استفاده می‌شود، زیرا این ضریب شاخصی بدون واحد است و برای مقایسه نسبت به کوواریانس مناسب‌تر است.

نامساوی کوشی، بعدها توسط «آمادئوس شوارتز» (Amandus Schwarz) دانشمند ریاضیدان آلمانی در سال ۱۸۸۸، به وسیله محاسبات انتگرالی اثبات شد و توسعه یافت.

نامساوی مارکف (Markov Inequality)

اگر متغیر تصادفی X نامنفی باشد، می‌توان بوسیله امید ریاضی X یک کران بالا برای احتمال $$P(X\geq a)$$ بدست آورد. در این حالت می‌نویسیم:

$$P(X\geq a)\leq\dfrac{E(X)}{a}$$

نامساوی مارکف و نامساوی‌های مشابه آن، یک کران (هر چند نادقیق) برای تابع توزیع احتمال برحسب امید ریاضی می‌سازند.

مثال ۳

فرض کنید X درآمد افراد باشد (درآمد در این حالت متغیر تصادفی نامنفی است) و داشته باشیم $$a=4E(X)$$. آنگاه می‌توان گفت حداکثر 25٪ افراد، درآمدی بیش از ۴ برابر میانگین دارند.

$$P(X\geq 4\times E(X))\leq\dfrac{E(X)}{4\times E(X)}=\dfrac{1}{4}=0.25$$

نامساوی چبیشف (Chebyshev Inequality)

فرض کنید X یک متغیر تصادفی با امید ریاضی $$E(X)$$ و واریانس متناهی $$Var(X)=\sigma^2$$ باشد. آنگاه برای هر عدد حقیقی مثبت مثل k‌ داریم:

$$P(|X-E(X)|\geq k\sigma)\leq \dfrac{1}{k^2}$$

این نامساوی نیز با توجه به واریانس و امید ریاضی یک کران بالا برای تابع احتمال متغیر تصادفی X در دم‌های سمت راست ایجاد می‌کند. اگر در نامساوی مارکف مقدار a را برابر با $$k\sigma^2$$ در نظر بگیریم و $$Y=[X-E(X)]^2$$ باشد،‌ قضیه چبیشف به راحتی اثبات می‌شود.

نامساوی جنسن (Jensen's Inequality)

فرض کنید X یک متغیر تصادفی و $$g(X)$$ نیز یک تابع «محدب» (Convex) باشد. در این حالت می‌توان رابطه زیر را بین امید ریاضی تابع X با تابعی از امید ریاضی X نوشت. یعنی در این شکل خواهیم داشت:

$$E(g(X))\geq g(E(X))$$

برای مثال با توجه به اینکه $$g(X)=X^2$$ یک تابع محدب است (زیرا مشتق دوم آن مثبت است)، نامساوی زیر برای آن صدق می‌کند.

$$E(X^2)\geq E^2(X)$$

با توجه به این موضوع مشخص است که واریانس مقداری نامنفی خواهد بود زیرا:

$$Var(X)=E(X^2)-E^2(X)\geq 0$$

مثال ۴

اگر $$g(X)=|X|$$ باشد با توجه به محدب بودن تابع قدر مطلق می‌توان نتیجه گرفت که $$|E(X)|\leq E(|X|)$$ در نتیجه اگر امید ریاضی برای قدرمطلق X وجود داشته باشد (امید ریاضی متناهی باشد)، بطور قطع نیز امید ریاضی متغیر تصادفی X وجود دارد. زیرا کران‌های مربوط به امید ریاضی متغیر تصادفی X برحسب امید ریاضی |X| نوشته می‌شوند.

$$|E(X)|\leq E(|X|)\rightarrow -E(|X|)\leq E(X)\leq E(|X|)$$