تحلیل تناظری (Correspondence Analysis) — پیاده سازی در R

۶۳۲ بازدید

آخرین به‌روزرسانی: ۰۸ خرداد ۱۴۰۲

زمان مطالعه: ۱۵ دقیقه

تحلیل تناظری (Correspondence Analysis) — پیاده سازی در R

یکی از تکنیک‌های آماری برای کاهش ابعاد «داده‌های طبقه‌ای» (Categorical Data)، استفاده از روش «تحلیل تناظری» (Correspondence Analysis) است که توسط «هرمان هارتلی» (Herman Otto Hartly) آمارشناس آلمانی در سال‌ ۱۹۵۰ ابداع شد. بعدها این تکنیک توسط آمارشناس فرانسوی «پائول بنزکری» ( Jean-Paul Benzécri) توسعه یافت. این روش درست به مانند روش «تحلیل مولفه‌های اصلی» (Principle Component Analysis) برای داده‌های کمی است. اغلب روش «تحلیل تناظری» را به اختصار «CA» می‌نامند. در تکنیک CA با استفاده از تفکیک «آماره کای ۲» مربوط به یک «جدول توافقی» (Contingency Table)، داده‌ها به عوامل عمود بر یکدیگر تجزیه می‌شوند.

فهرست مطالب این نوشته

تحلیل تناظری (Correspondence Analysis - CA)

خلاصه و جمع‌بندی

در این نوشتار به منظور پیاده‌سازی محاسبات مربوط به تکنیک CA از «بسته نرم‌افزاری» (Package) به نام "FactoMineR" در زبان برنامه‌نویسی محاسبات آماری R استفاده خواهیم کرد. همچنین برای نمایش نتایج حاصل از تحلیل CA از دستوراتی استفاده خواهیم کرد که به کمک بسته "factoextra" قابل دسترس هستند. البته دستورات و بسته‌های آماری دیگری مانند "MASS" و "ca" نیز محاسبات مربوط به تحلیل تناظری را در زبان برنامه‌نویسی R انجام می‌دهند. همچنین از برنامه‌های محاسبات آماری دیگر مانند SPSS نیز برای اجرای تحلیل تناظری می‌توان استفاده کرد.

برای آگاهی بیشتر با توزیع کای ۲ و متغیر تصادفی آن بهتر است نوشتار متغیر تصادفی و توزیع کای 2 (Chi Squared) — مفاهیم و کاربردها و آزمون‌ نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای2 را مطالعه کنید. همچنین مطالعه مطلب تحلیل مولفه اساسی (PCA) — راهنمای عملی به همراه کد نویسی در پایتون و R نیز خالی از لطف نیست.

تحلیل تناظری (Correspondence Analysis - CA)

هدف در «تحلیل تناظری»، ایجاد مولفه‌هایی از داده‌ها است که به صورت ترکیب خطی از آن‌ها تولید شده و بر یکدیگر عمود باشند. به این ترتیب اگر یک «جدول توافقی» (Contingency Table) را برای نمایش «داده‌های طبقه‌ای» (Categorical Data) به کار ببریم، تحلیل تناظری سعی در ایجاد مولفه‌هایی از سطرها و ستون‌ها دارد که نسبت به یکدیگر مستقل باشند در نتیجه می‌توانیم اطلاعات درون یک جدول توافقی را به صورت مولفه‌هایی مستقل از هم درآوریم.

فیلم آموزش نمونه گیری در نرم افزار آر R در فرادرس

کلیک کنید

باید توجه داشت که مقادیر موجود در جدول توافقی برای تحلیل تناظری باید با یک مقیاس اندازه‌گیری شده باشند. برای مثال همگی از طریق شمارش یا درصدگیری بدست آیند. در تحلیل CA، سطرهای و ستون‌ها به شکل یکسان در تشکیل مولفه‌ها تاثیرگذار هستند. در این روش، آماره کای ۲ که مرتبط با جدول توافقی است به دو مولفه عمود بر هم تفکیک می‌شود. به این منظور باید روی جدول توافقی مورد نظر، محاسباتی را به عنوان پیش‌پردازش انجام دهیم. در ادامه این عملیات معرفی می‌شوند.

پیش‌پردازش جدول توافقی

فرض کنید $$C$$ یک ماتریس $$m \times n$$ باشد. به این معنی که این ماتریس دارای $$m$$ سطر و $$n$$ ستون است. درست شبیه روشی که در «تحلیل مولفه‌های اصلی» داشتیم، برای ایجاد جدول توافقی مورد نظر، لازم است که به مقادیر مربوط به سطرها و ستون‌ها، وزن‌های متناسبی بدهیم تا مولفه‌ها بدست آیند. در اینجا اگر مولفه‌های مربوط به سطر iام و ستون jام را با $$C_{ij}$$‌ نشان دهیم، وزن متناسب برای سطر $$m$$ام به صورت زیر نوشته می‌شود.

$$\large {\displaystyle w_{m}={\frac {1}{n_{C}}}C {1} }$$

همچنین برای ستون‌ها نیز وزن متناسب براساس رابطه زیر محاسبه می‌شود.

$$\large {\displaystyle w_{n}={\frac {1}{n_{C}}} {1} ^{T}C}$$

در رابطه‌های بالا، مقدار $$n_c$$ برابر با مجموع مقادیر سطرها و ستونی‌های جدول توافقی است، یعنی داریم.

$$\large {\displaystyle n_{C}=\sum _{i=1}^{n}\sum _{j=1}^{m}C_{ij}}$$

از طرفی $$1$$ نیز بردار ستونی با مقادیر ۱ است که دارای تعداد سطرهای متناسب با ماتریس مربوط به جدول توافقی است.

در گام بعدی ماتریس یا جدول $$S$$ براساس جدول $$C$$ طبق رابطه زیر محاسبه می‌شود.

$$\large {\displaystyle S={\frac {1}{n_{C}}}C}$$

در انتهای مراحل پیش‌پردازش نیز ماتریس یا جدول نهایی به نام $$M$$ برای تشکیل مولفه‌ها آماده می‌شود.

$$\large {\displaystyle M=S-w_{m}w_{n}}$$

با توجه به مبنای محاسبات برای وزن‌ سطرها و ستون‌ها، مشخص است که $$w_m$$ «احتمال حاشیه‌ای» (Marginal Probability) برای هر یک از سطرها (مقادیر متغیر طبقه‌ای اول) است. همینطور توسط $$w_n$$ نیز «احتمال حاشیه‌ای» برای هر ستون (مقادیر متغیر طبقه‌ای دوم) را محاسبه کرده است. به همین ترتیب ماتریس یا جدول $$S$$ نیز همان «توزیع احتمال توام» (Joint Probability Distribution) سطرها و ستون‌ها است.

به این ترتیب ماتریس $$M$$ بیانگر انحراف از استقلال است، زیرا اختلاف حاصلضرب احتمال‌های حاشیه‌ای را از تابع احتمال توام می‌سنجد. در مراحل تحلیل CA این انحرافات، به صورت مربع (توان دو) در آمده و به طور مناسب مقیاس‌بندی می‌شوند تا با جمع آن‌ها آماره کای ۲ مربوط به جدول $$C$$ بدست آید.

مولفه‌های عمود بر هم (Orthogonal Components)

به منظور تفکیک ماتریس یا جدول $$M$$ از همان روش «تجزیه مقادیر تکین تعمیم یافته» (Generalized Singular Value Decomposition) استفاده می‌شود. وزن مولفه‌ها در این روش، ماتریس‌های قطری $$W_m$$ و $$W_n$$ هستند که در ادامه معرفی می‌شوند.

$$\large {\displaystyle W_{m}=\operatorname {diag} \{1/w_{m}\}}$$

$$\large {\displaystyle W_{n}=\operatorname {diag} \{1/w_{n}\}}$$

نکته: منظور از ماتریس قطری (Diagonal Matrix) که در رابطه‌ها بالا با $$diag$$ نشان داده شده، ماتریسی است که عناصر خارج از قطر اصلی آن صفر هستند و عناصر روی قطر اصلی آن به صورت معکوس وزن‌‌ سطرها و ستون‌ها یعنی $$\dfrac{1}{w_n}$$ یا $$\dfrac{1}{w_m}$$ در نظر گرفته شده است.

به این ترتیب به کمک روش «تجزیه مقادیر تکین تعمیم یافته»، ماتریس $$M$$‌ را به بردارهای $$U$$ و $$V^*$$ و ماتریس $$\Sigma$$ تجزیه می‌کنیم. در این حالت رابطه زیر برقرار است.

$$\large M=U\Sigma V^{*}$$

در رابطه بالا، تساوی‌ها زیر برای $$U$$ و $$V$$ برقرار است.

$$\large U^{*}W_{m}U=V^{*}W_{n}V=I$$

واضح است که منظور از $$I$$‌ ماتریس «یکه» (Identity Matrix) است که ماتریسی قطری با عناصر ۱ در قطر اصلی آن است همچنین $$U$$ و $$V$$ نیز بردارهای «یکامتعامد» (Orthonormal) هستند به این معنی که بر یکدیگر عمود بوده و طولی برابر با واحد دارند. از طرفی، ماتریس‌های $$W_n$$ و $$W_m$$ که وزن‌ها را برای مولفه‌ها مشخص می‌کنند، «معین مثبت» (Positive Definite) خواهند بود.

با توجه به محاسبات بالا، عوامل یا مولفه‌ها، مطابق با رابطه‌های زیر ایجاد می‌شوند.

$$\large {\displaystyle F_{m}=W_{m}U\Sigma }$$

$$\large {\displaystyle F_{n}=W_{n}V\Sigma}$$

مولفه سطری و ستونی برای ماتریس یا جدول $$C$$ با نام $$F_m$$ و $$F_n$$ طبق محاسبه‌های بالا نام‌گذاری شده‌اند.

گونه‌های مختلفی از تکنیک CA وجود دارد. برای مثال روش تحلیل «تناظری بی‌روند شده» (Detrended Correspondence Analysis) که به اختصار DCA نامیده می‌شود از این گونه محسوب می‌شود. همچنین «تحلیل تناظری کانونی» (Canonical Correspondence Analysis) یکی از روش‌های تحلیل تقلیل داده‌ها برای مقادیر طبقه‌ای است که تقریبا مشابه روش CA است. همچنین تکنیک‌های «تحلیل ممیزی» (Discriminant Analysis) برای داده‌های کیفی و طبقه‌ای به کمک روش‌های CA‌ اجرا می‌شوند. در حالت چند متغیره، «تحلیل تناظری چندگانه» (Multiple Correspondence Analysis) نیز به کار می‌آید.

به منظور پیاده‌سازی محاسبات گفته شده برای تحلیل تناظری، نرم‌افزارهای مختلفی وجود دارد. لیست زیر به معرفی بعضی از این برنامه‌ها پرداخته است.

سیستم تصویرسازی داده‌ها (Data Visualization System) به نام «Orange» و ماژول «orngCA».
بسته‌های محاسباتی در نرم‌افزار R به نام‌های MASS, ade4, ca, vegan, Exposition و FactoMineR.
بسته آماری SPSS و دستور Correspondence Analysis از فهرست Analysis و گزینه Dimension Reduction.

در قسمت بعدی به نرم‌افزار R تکیه کرده و محاسبات مربوط به تحلیل تناظری را با بسته FactoMineR‌ اجرا خواهیم کرد.

تحلیل تناظری در R

در این بخش، به تحلیل یک جدول توافقی دو بعدی می‌پردازیم و وزن‌ها یا امتیازات (Factor Score) مربوط به هر بُعد و نقاط موجود در سطر و ستون‌های جدول توافقی را محاسبه می‌کنیم. همچنین به کمک نمودارهایی مولفه‌ها ایجاد شده را تحلیل خواهیم کرد.

فیلم آموزش برنامه نویسی R و نرم افزار RStudio – تکمیلی در فرادرس

کلیک کنید

در حقیقت هدف از تحلیل تناظری، پیدا کردن سطرهایی از جدول توافقی است که با ستون‌ها دارای رابطه هستند و به این ترتیب می‌توانیم به کمک تشکیل مولفه‌های جدید، تعداد سطرها یا ستون‌های جدول توافقی را کاهش دهیم. در ادامه به بررسی داده‌هایی مربوط به جدول توافقی دو طرفه‌ای خواهیم پرداخت که مرتبط با کارهای منزل توسط زن و مرد است که بینشان تقسیم شده. به این ترتیب با استفاده از تکنیک CA می‌توانیم کارهایی که براساس جنسیت مستقل است را شناسایی کنیم. به این ترتیب جدول توافقی ابعاد کمتری خواهد داشت.

بارگذاری کتابخانه‌ها و تحلیل توصیفی داده‌ها

ابتدا کتابخانه‌های مورد نیاز را در R بارگذاری می‌کنیم.

1install.packages(c("FactoMineR", "factoextra", "ggplot2","corrplot"))
2library("FactoMineR")
3library("ggplot2")
4library("factoextra")
5library("corrplot")

نکته: برای استفاده از بسته factoextra باید کتابخانه ggplot2‌ نیز قبلا نصب شده باشد.

حال داده‌های مربوط به جدول توافقی که وظایف خانه را به تفکیک چهار شکل مختلف (Wife, Alternaintg, Husband, Jointly) طبقه‌بندی کرده است، از کتابخانه factoextra فراخوانی می‌کنیم.

مقدارهای درون جدول توافقی برای ستون با مقدار (Wife) مربوط به تعداد وظایفی است که «همسر» در خانه انجام داده است. همچنین (Alternating‌) نشانگر تعداد وظایفی است که به صورت «دوره‌‌ای» بین زن و مرد در خانه چرخش دارد. ستون (Husband) هم تعداد وظایفی را در خانه نشان می‌دهد که توسط «شوهر» صورت گرفته است. در انتها نیز (Jointly) وظایفی را که به صورت «همکاری» در خانه انجام شده، شمارش کرده است.

1data(housetasks)
2head(housetasks)

همانطور که دیده می‌شود داده‌های این جدول، دارای ۱۳ وظیفه یا کار در منزل است که بین زوج‌ (زن و مرد) تقسیم شده است. در حقیقت این داده‌ها تشکیل یک جدول توافقی را داده‌اند.

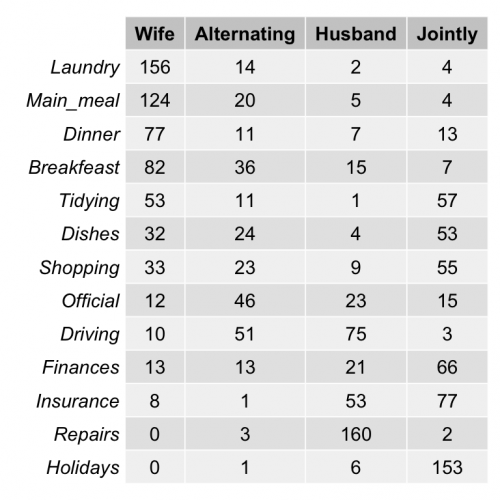
correspondence-analysis task table

به نظر می‌رسد که این جدول توافقی دارای دو متغیر طبقه‌ای است. متغیر اول (متغیر سطری) که «وظایف» (task) را نشان می‌دهد، دارای ۱۳ نوع یا مقدار مختلف است. از طرفی شیوه انجام وظایف به عنوان متغیر دوم (متغیر ستونی) نیز دارای چهار گونه یا نوع است. فراوانی‌ (Frequency) مربوط به مقادیر سطرهای و ستون‌ها نیز درون جدول توافقی قرار گرفته است.

از آنجایی که این جدول دارای سطرها و ستون‌های زیادی نیست، می‌توان بدون انجام دادن محاسبات پیچیده، اطلاعات مناسبی را از آن دریافت کرد.

بعضی از وظایف مانند «لباس شویی» (Laundry)، «پخت ناهار» (Main_Meal) و «تهیه شام» (Dinner) بیشتر توسط خانم خانه صورت گرفته است.
یبشتر موارد «تعمیراتی» (Repairs) و رانندگی (Driving) نیز توسط شوهر انجام می‌شود.
«گردش و تفریح» (Holidays) نیز در اکثر مواقع به صورت دسته‌جمعی بوده است.

به کمک دستورات زیر، اطلاعات مربوط به این جدول را به صورت یک «نمودار حبابی» (Balloon Chart) دو بُعدی در خواهیم آورد. البته توجه داشته باشید که ابتدا این «چارچوب داده» (Data Frame) به قالب یک ماتریس (as.matrix) و سپس جدول (as.table) درآمده است.

1# 1. convert the data as a table
2dt <- as.table(as.matrix(housetasks))
3# 2. Graph
4p <- ggplot(as.data.frame(t(dt)) 
5            ,aes(x =Var1, y = Var2))
6p+geom_point(aes(size=Freq),shape=21, colour="black", fill="skyblue")+
7 theme(panel.background=element_blank(), panel.border = element_rect(colour = "blue", fill=NA, size=1))+
8  scale_size_area(max_size=15)+
9  labs(x="Doing By", y="Tasks")

نتیجه اجرای این دستورات مطابق با نموداری است که در تصویر زیر مشخص شده است.

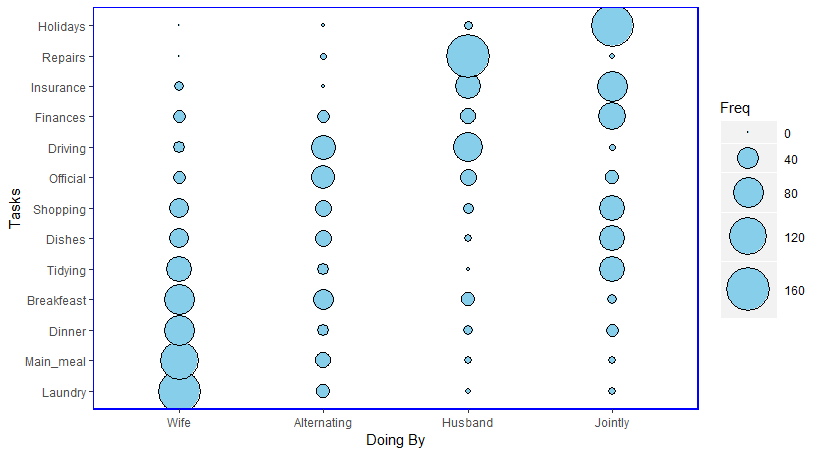
balloon plot 2d

اگر جدول توافقی دارای تعداد سطرها و ستون‌هایی زیادی نباشد، براساس آماره کای ۲ می‌توان استقلال دو متغیر تصادفی طبقه‌ای مربوط به سطر و ستون را آزمون کرد. این کار توسط دستور زیر و تابع chisq.test صورت گرفته است. کافی است به عنوان پارامتر، «مجموعه داده» (Data.frame) مورد نظرتان را مشخص کنید.

1chisq <- chisq.test(housetasks)
2chisq

خروجی اجرای این دستور به صورت زیر در خواهد آمد. مشخص است که با توجه به کوچک بودن p-value، به رد فرض صفر (استقلال متغیرهای سطر و ستون) رای می‌دهیم. به این ترتیب به نظر می‌رسد که نوع وظیفه در خانه به جنسیت زوج بستگی دارد.

1## 
2##  Pearson's Chi-squared test
3## 
4## data:  housetasks
5## X-squared = 2000, df = 40, p-value <2e-16

به این ترتیب به نظر می‌رسد که به کمک تحلیل CA می‌توانیم مولفه‌هایی از سطر و ستون جدول توافقی پیدا کنیم که با حفظ استقلال، بیشترین اطلاعات را نیز به ما بدهد.

تحلیل CA با کتابخانه FactoMineR

اگر می‌خواهید تحلیل CA را در زبان برنامه‌نویسی آماری R انجام دهید، بهتر است از کتابخانه FactoMineR و تابع CA استفاده کنید. شکل دستوری برای این تابع به صورت زیر است. البته پارامترهای تابع CA نیز در ادامه معرفی می‌شوند.

1CA(X, ncp = 5, graph = TRUE)

پارامتر X: جدول توافقی است که به صورت یک مجموعه داده یا ماتریس است.
پارامتر ncp: این پارامتر، تعداد مولفه‌های اصلی (ابعاد نهایی) را مشخص می‌کند. در اینجا مقدار ۵ به عنوان پیش‌فرض در نظر گرفته شده است.
پارامتر graph: اگر می‌خواهید نمودار مربوط به تجزیه و تحلیل تناظری در قالب یک نمودار نقطه‌ای ظاهر شود، مقدار این پارامتر را TRUE انتخاب کنید.

بنابراین اگر دستور زیر را اجرا کنیم، تحلیل تناظری براساس داده‌های housetasks و به همراه نمودار آن ظاهر می‌شود.

1res.ca <- CA(housetasks, graph = TRUE)

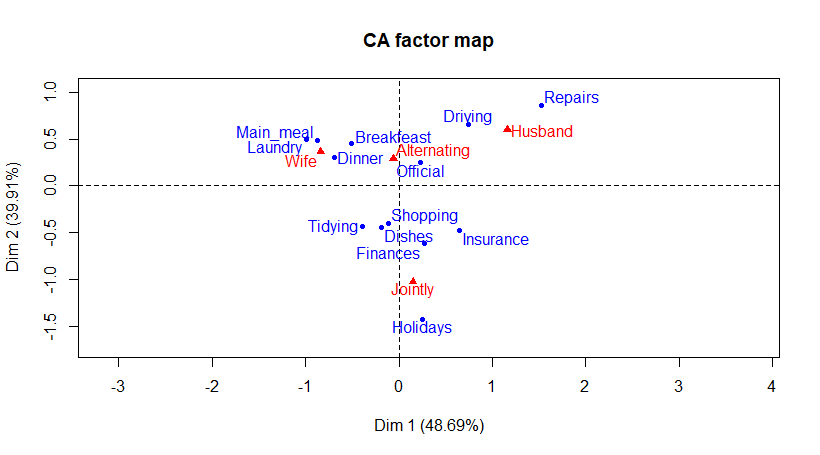
ca plot in 2 dim

مختصاتی که برای هر نقطه در این نمودار دیده می‌شود، همان ضرایب مولفه‌های سطری و ستونی است که در خروجی و اطلاعات بعدی به صورت Dim1 و Dim2 برای سطر و ستون (نقاط آبی و قرمز رنگ) نمایش داده شده است. وظایفی که در قسمت چپ نمودار دیده می‌شود به دلیل نزدیکی به متغیر Wife، به نظر مربوط به خانم خانه است. از طرفی وظایفی که در سمت راست نمودار و نزدیک به Husband قرار دارند، مرتبط با کارهایی است که شوهر به عهده دارد. همچنین در مرکز نمودار وظایفی که زن و شوهر به صورت «دوره‌ای» (Alternating) یا «همکاری» (Jointly) انجام می‌دهند، دیده می‌شود.

خروجی دستور CA را به کمک دستور summary نیز می‌توانید نمایش دهید.

1summary(res.ca)

1Call:
2CA(X = housetasks, graph = TRUE) 
3
4The chi square of independence between the two variables is equal to 1944.456 (p-value =  0 ).
5
6Eigenvalues
7                       Dim.1   Dim.2   Dim.3
8Variance               0.543   0.445   0.127
9% of var.             48.692  39.913  11.395
10Cumulative % of var.  48.692  88.605 100.000
11
12Rows (the 10 first)
13              Iner*1000     Dim.1     ctr    cos2     Dim.2     ctr    cos2  
14Laundry     |   134.160 |  -0.992  18.287   0.740 |   0.495   5.564   0.185 |
15Main_meal   |    90.692 |  -0.876  12.389   0.742 |   0.490   4.736   0.232 |
16Dinner      |    38.246 |  -0.693   5.471   0.777 |   0.308   1.321   0.154 |
17Breakfeast  |    41.124 |  -0.509   3.825   0.505 |   0.453   3.699   0.400 |
18Tidying     |    24.667 |  -0.394   1.998   0.440 |  -0.434   2.966   0.535 |
19Dishes      |    19.587 |  -0.189   0.426   0.118 |  -0.442   2.844   0.646 |
20Shopping    |    14.970 |  -0.118   0.176   0.064 |  -0.403   2.515   0.748 |
21Official    |    53.300 |   0.227   0.521   0.053 |   0.254   0.796   0.066 |
22Driving     |   101.509 |   0.742   8.078   0.432 |   0.653   7.647   0.335 |
23Finances    |    29.564 |   0.271   0.875   0.161 |  -0.618   5.559   0.837 |
24              Dim.3     ctr    cos2  
25Laundry      -0.317   7.968   0.075 |
26Main_meal    -0.164   1.859   0.026 |
27Dinner       -0.207   2.097   0.070 |
28Breakfeast    0.220   3.069   0.095 |
29Tidying      -0.094   0.489   0.025 |
30Dishes        0.267   3.634   0.236 |
31Shopping      0.203   2.223   0.189 |
32Official      0.923  36.940   0.881 |
33Driving       0.544  18.596   0.233 |
34Finances      0.035   0.062   0.003 |
35
36Columns
37              Iner*1000     Dim.1     ctr    cos2     Dim.2     ctr    cos2  
38Wife        |   301.019 |  -0.838  44.462   0.802 |   0.365  10.312   0.152 |
39Alternating |   117.824 |  -0.062   0.104   0.005 |   0.292   2.783   0.105 |
40Husband     |   381.373 |   1.161  54.234   0.772 |   0.602  17.787   0.208 |
41Jointly     |   314.725 |   0.149   1.200   0.021 |  -1.027  69.118   0.977 |
42              Dim.3     ctr    cos2  
43Wife         -0.200  10.822   0.046 |
44Alternating   0.849  82.549   0.890 |
45Husband      -0.189   6.133   0.020 |
46Jointly      -0.046   0.495   0.002 |

همانطور که دیده می‌شود در ابتدای خروجی، مقدار آماره کای ۲ و مقدار احتمال (p-value) مشاهده می‌شود. مشخص است که فرض استقلال سطر و ستون رد شده و به نظر می‌رسد بین آن‌ها رابطه‌ای وجود دارد. این رابطه نشان می‌دهد که بعضی از کارها توسط شوهر و بعضی نیز توسط زن انجام می‌شود.

در قسمت مقادیر ویژه (EigenValues)، میزان واریانس برای هر مولفه دیده می‌شود. این لیست براساس مقدارهای واریانس مولفه‌ها از بزرگ به کوچک مرتب شده. بنابراین مولفه اول (Dim1) بیشترین واریانس و آخرین مولفه نیز کمترین واریانس را دارد.

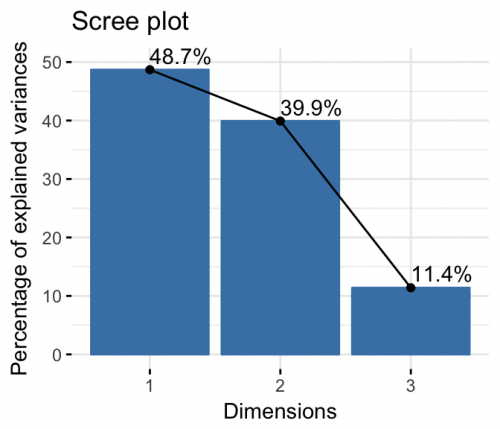
از طرفی حدود 50٪ (48.69٪) تغییرات یا واریانس در مولفه اول و 40٪ (39.93٪) نیز در مولفه دوم قرار گرفته است. در مجموع (Cumulative % of Var) حدود ۸۹٪ تغییرات یا واریانس توسط این دو مولفه بیان شده است، بنابراین استفاده از دو مولفه کافی به نظر می‌رسد. این اطلاعات در سطرهای بعدی قسمت مقادیر ویژه دیده می‌شود.

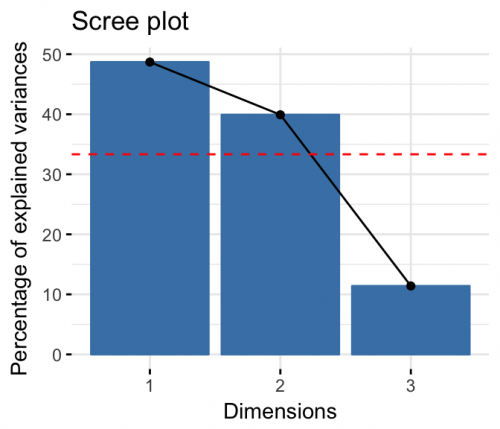
اگر می‌خواهید تغییر واریانس را برای بُعدها ترسیم کنید، نمودار بازویی (Elbow) مناسب به نظر می‌رسد. در بحث مربوط به مولفه‌ها و تحلیل تناظری به چنین نموداری Scree Plot گفته می‌شود. در این نمودار، مقادیر ویژه ماتریس $$M$$ به ترتیب از بزرگ به کوچک مرتب شده و به صورت یک نمودار ستونی به همراه یک نمودار خطی نشان داده می‌شود. برای ترسیم چنین نموداری از کد زیر استفاد کنید.

1fviz_screeplot(res.ca, addlabels = TRUE, ylim = c(0, 50))

خروجی مطابق با تصویر زیر خواهد بود.

correspondence-analysis-eigenvalue-screeplot

اگر داده‌ها جدول توافقی به صورت تصادفی (مستقل از یکدیگر) بودند، مقدار ویژه برای سطر و ستون جدول توافقی به صورت زیر بدست می‌آیند.

$$\large Eigen_R=\dfrac{1}{nrow-1}=\dfrac{1}{12}=8.33\%$$

$$\large Eigen_C=\dfrac{1}{ncol-1}=\dfrac{1}{3}=33.33\%$$

معمولا مولفه‌هایی که از بیشینه مقادیر ویژه حالت تصادفی بزرگتر باشند از اهمیت بیشتری برخوردارند. پس به نظر می‌رسد که مولفه اول و دوم برای بیان تغییرات در جدول توافقی کافی باشند. این موضوع را به کمک ترسیم نمودار زیر نیز نشان داده‌ایم. خط قرمز رنگ همان حداکثر مقدارهای ویژه سطر و ستون در حالت تصادفی بودن جدول توافقی است.

1fviz_screeplot(res.ca) +
2 geom_hline(yintercept=33.33, linetype=2, color="red")

correspondence-analysis-scree-plot-cut-off

دوباره به نتایج خروجی تحلیل تناظری بر می‌گردیم.

1Rows (the 10 first)
2              Iner*1000     Dim.1     ctr    cos2     Dim.2     ctr    cos2  
3Laundry     |   134.160 |  -0.992  18.287   0.740 |   0.495   5.564   0.185 |
4Main_meal   |    90.692 |  -0.876  12.389   0.742 |   0.490   4.736   0.232 |
5Dinner      |    38.246 |  -0.693   5.471   0.777 |   0.308   1.321   0.154 |
6Breakfeast  |    41.124 |  -0.509   3.825   0.505 |   0.453   3.699   0.400 |
7Tidying     |    24.667 |  -0.394   1.998   0.440 |  -0.434   2.966   0.535 |
8Dishes      |    19.587 |  -0.189   0.426   0.118 |  -0.442   2.844   0.646 |
9Shopping    |    14.970 |  -0.118   0.176   0.064 |  -0.403   2.515   0.748 |
10Official    |    53.300 |   0.227   0.521   0.053 |   0.254   0.796   0.066 |
11Driving     |   101.509 |   0.742   8.078   0.432 |   0.653   7.647   0.335 |
12Finances    |    29.564 |   0.271   0.875   0.161 |  -0.618   5.559   0.837 |
13              Dim.3     ctr    cos2  
14Laundry      -0.317   7.968   0.075 |
15Main_meal    -0.164   1.859   0.026 |
16Dinner       -0.207   2.097   0.070 |
17Breakfeast    0.220   3.069   0.095 |
18Tidying      -0.094   0.489   0.025 |
19Dishes        0.267   3.634   0.236 |
20Shopping      0.203   2.223   0.189 |
21Official      0.923  36.940   0.881 |
22Driving       0.544  18.596   0.233 |
23Finances      0.035   0.062   0.003 |
24
25Columns
26              Iner*1000     Dim.1     ctr    cos2     Dim.2     ctr    cos2  
27Wife        |   301.019 |  -0.838  44.462   0.802 |   0.365  10.312   0.152 |
28Alternating |   117.824 |  -0.062   0.104   0.005 |   0.292   2.783   0.105 |
29Husband     |   381.373 |   1.161  54.234   0.772 |   0.602  17.787   0.208 |
30Jointly     |   314.725 |   0.149   1.200   0.021 |  -1.027  69.118   0.977 |
31              Dim.3     ctr    cos2  
32Wife         -0.200  10.822   0.046 |
33Alternating   0.849  82.549   0.890 |
34Husband      -0.189   6.133   0.020 |
35Jointly      -0.046   0.495   0.002 |

ضرایب مربوط به سطر‌ها در قسمت Rows و ضرایب ستون‌ها نیز در بخش Columns‌ دیده می‌شود. وزن مربوط به هر مولفه در سطر در قسمت Rows و پیش‌وند Dim نشان داده شده است.

در این بخش، ستون «inertia»، مربوط به «اینرسی» سطر‌ها یا ستون‌ها است. به این معنی که اینرسی هر سطر (یا ستون) توسط حاصلضرب احتمال حاشیه‌ای در مربع «فاصله» (Distance) آن سطر از مرکز بدست می‌آید. در اینجا شیوه محاسبه فاصله براساس فاصله کای ۲ در نظر گرفته شده است. هرچه مقدار اینرسی برای هر سطر بیشتر باشد به معنی ارتباط بیشتر آن مولفه با آن سطر است.

نکته: برای آنکه بتوان مقدارهای مربوط به اینرسی را بهتر مقایسه کرد،‌ در این جدول مقادیرشان در ۱۰۰۰ ضرب شده است.

از طرفی در ستون cos2 نیز مربع کسینوس زاویه‌ای که هر مقدار با آن مولفه (یا بُعد) ایجاد می‌کند، مشخص شده است. به این طریق نیز می‌توان شدت رابطه را بین مولفه یا بُعد و هر مقدار از متغیرها، مشخص کرد. این زوایه‌ها را در نمودار ترسیم شده، می‌توانید با رسم یک خط از مرکز به نقطه‌های درون نمودار تشخیص دهید. به این ترتیب ستون cos2 نشان می‌دهد که روی محور Dim1 یا Dim2 زاویه‌ای که متغیر ایجاد کرده است دارای چه مقداری است. به این ترتیب کیفیت بیان هر ویژگی یا مقدار متغیر سطر یا ستون، توسط مولفه‌ها تعیین می‌شود.

اگر می‌خواهید مقدارهای cos2 را برای سطر یا ستون مشاهده کنید از دستور زیر استفاده کنید.

1row <- get_ca_row(res.ca)
2col<-get_ca_col(res.ca)
3row$cos2
4col$cos2

خروجی به صورت زیر خواهد بود.

1> row$cos2
2                Dim 1      Dim 2       Dim 3
3Laundry    0.73998741 0.18455213 0.075460467
4Main_meal  0.74160285 0.23235928 0.026037873
5Dinner     0.77664011 0.15370323 0.069656660
6Breakfeast 0.50494329 0.40023001 0.094826699
7Tidying    0.43981243 0.53501508 0.025172490
8Dishes     0.11811778 0.64615253 0.235729693
9Shopping   0.06365362 0.74765514 0.188691242
10Official   0.05304464 0.06642648 0.880528877
11Driving    0.43201860 0.33522911 0.232752289
12Finances   0.16067678 0.83666958 0.002653634
13Insurance  0.57601197 0.30880208 0.115185951
14Repairs    0.70673575 0.22587147 0.067392778
15Holidays   0.02979239 0.96235977 0.007847841
16> col$cos2
17                  Dim 1     Dim 2       Dim 3
18Wife        0.801875947 0.1524482 0.045675847
19Alternating 0.004779897 0.1051016 0.890118521
20Husband     0.772026244 0.2075420 0.020431728
21Jointly     0.020705858 0.9772939 0.002000236

نکته: مجموع مقدار cos2 برای هر سطر برای همه مولفه‌ها برابر با ۱ است. بنابراین اگر برای مثال مجموع مقدار cos2 برای دو مولفه در یک سطر به مقدار ۱ نزدیک باشد، می‌توان گفت که این سطر توسط این دو مولفه به خوبی توصیف شده است و احتیاجی به مولفه‌های دیگر نیست.

برای نمایش همزمان مقدار کسینوس این زاویه‌ها (شدت رابطه) با مولفه‌‌ها بهتر است از دستور زیر استفاده کنید. تابع fviz_ca_row از توابع مربوط به کتابخانه factoextra است. به این ترتیب ارتباط بین متغیرهای مربوط به سطر را با مولفه‌های آن خواهید دید.

1# Color by cos2 values: quality on the factor map
2fviz_ca_row(res.ca, col.row = "cos2",
3             gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), 
4             repel = TRUE)

نتیجه نموداری به صورت زیر خواهد بود.

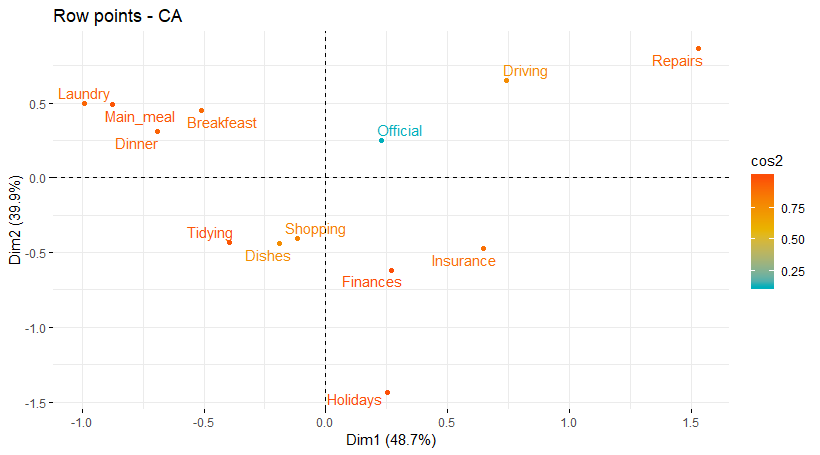
row points ca

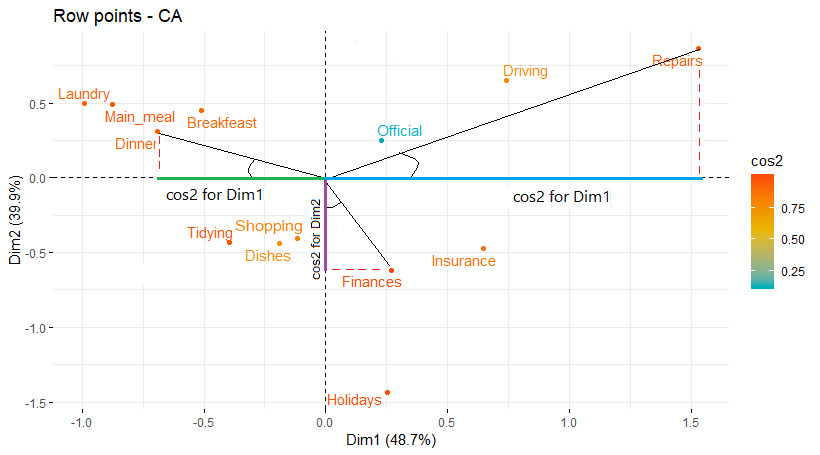
برای درک مفهوم کسینوس این زاویه‌ها، به تصویر زیر توجه کنید. هر چه میزان کسیونس (یا توان دوم آن) یک مقدار روی محورها بزرگتر باشد، نشانگر توصیف بهتر آن مقدار توسط مولفه است. البته توجه داشته باشید که بردارهای ترسیم شده به رنگ آبی، سبز و بنفش در تصویر زیر متناسب با مقدار cos2 هستند زیرا مشخص است که مقدار cos2 بزرگتر از ۱ نخواهد بود.

row points ca - and cosine

همین عمل را هم برای متغیرهای ستون انجام می‌دهیم.

1fviz_ca_col(res.ca, col.col = "cos2",
2            gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), 
3            repel = TRUE)

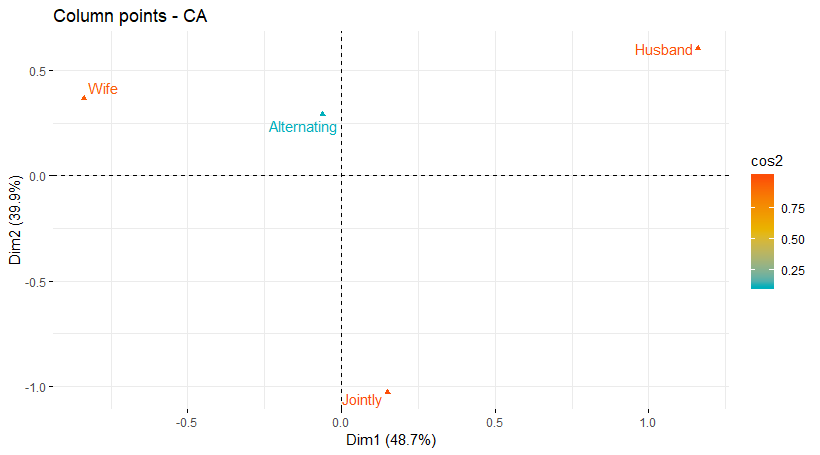
column points ca

این نمودارها نشان می‌دهند که برای تشخیص کارهای «دوره‌ای» (Alternating) و «همکاری» که به عنوان بعضی از مقادیر متغیر ستون شناخته شده‌اند، توسط این دو مولفه به خوبی صورت گرفته است ولی کارهایی که مربوط به مردان و زنان است به خوبی قابل تشخیص است.

از طرفی تفکیکی نیز برای مقدارهای متغیر مربوط به سطر‌ها، توسط مولفه‌ها ایجاد شده است. به نظر می‌رسد که وظایف به سه دسته تقسیم شده‌اند. اگر محور افقی (مولفه اول) را مرتبط با وظایف روزمره بدانیم، می‌توانیم مقدارهای آن را براساس Repairs, Laundry, Main_meal, Dinner, Breakfeast, Tidying در نظر بگیریم. برای محور عمودی (مولفه دوم) نیز کارهایی که مرتبط با زمان یا دوره خاصی هستند، دیده می‌شود. برای مثال Finances, Holidays می‌توانند مولفه دوم را تعیین کنند.

نکته: مقدارهایی از متغیر سطری که به صورت کمرنگ یا آبی در نمودار دیده می‌شوند به علت تعلق کمتر به مولفه اول و دوم می‌توانند مبنایی برای تشکیل مولفه سوم باشند.

نمایش اهمیت هر مقدار از متغیر سطر یا ستون برای مولفه‌ها را به کمک نمودار حبابی نیز می‌توان نشان داد. دستور زیر به این منظور از کتابخانه (corrplot) به کار رفته است.

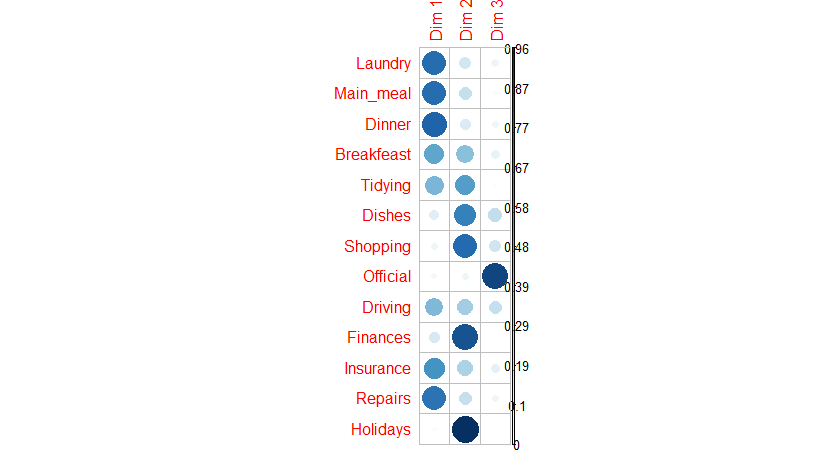
1corrplot(row$cos2, is.corr=FALSE)
2corrplot(col$cos2, is.corr=FALSE)

corrplot row - نمایش میزان همبستگی متغیرهای سطر با ابعاد حاصل از تحلیل CA

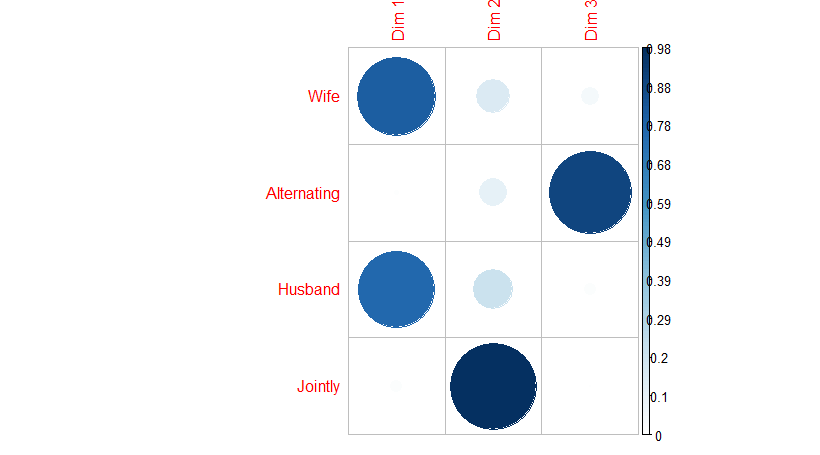
corrplot column - نمایش میزان همبستگی متغیرهای ستون با ابعاد حاصل از تحلیل CA

خلاصه و جمع‌بندی

همانطور که مشاهده شده، به کمک تکنیک CA، داده‌های مربوط به جدول توافقی دو طرفه با چندین مقدار برای سطر و ستون، به دو مولفه با توجه به وزن‌های استخراج شده، تبدیل شد. با توجه به مثالی که محاسبات آن به کمک دستورات زبان برنامه نویسی R صورت گرفت، مشخص شد که مقادیر Alternating, Jointly از ستون و Official از سطر برای تشخیص یا تفکیک وظایف براساس جنسیت تاثیرگذار نیستند، بنابراین می‌توانیم آن‌ها را از مدل جدول توافقی خارج کنیم. به این ترتیب به نظر می‌رسد، بدون در نظر گرفتن این مقدارها، بتوان به نتایج مشابه آماری در تجزیه و تحلیل داده‌ها رسید.

فیلم آموزش داده کاوی و زبان برنامه نویسی R (رایگان) در فرادرس

کلیک کنید

بنابراین با این کار عمل «تقلیل داده‌های طبقه‌ای» (Categorical Data Reduction) در جدول توافقی صورت گرفته است. البته مشخص است که رسم نمودار Scree plot نیز در تشخیص تعداد مولفه‌ها یا فاکتورهای مناسب بسیار موثر است.

در ادامه برنامه کامل مربوط به تحلیل تناظری برای مثال وظایف منزل را مشاهده می‌کنید.

1install.packages(c("FactoMineR", "factoextra", "ggplot2","corrplot"))
2library("FactoMineR")
3library("factoextra")
4library("ggplot2")
5library("corrplot")
6data(housetasks)
7head(housetasks)
8chisq <- chisq.test(housetasks)
9chisq
10# 1. convert the data as a table
11dt <- as.table(as.matrix(housetasks))
12# 2. Graph
13p <- ggplot(as.data.frame(t(dt)) 
14            ,aes(x =Var1, y = Var2))
15p+geom_point(aes(size=Freq),shape=21, colour="black", fill="skyblue")+
16 theme(panel.background=element_blank(), panel.border = element_rect(colour = "blue", fill=NA, size=1))+
17  scale_size_area(max_size=15)+
18  labs(x="Doing By", y="Tasks")
19
20res.ca=CA(housetasks, ncp=5,graph = TRUE)
21cc$call$marge.row
22summary(res.ca)
23
24
25fviz_screeplot(res.ca, addlabels = TRUE, ylim = c(0, 50))
26
27fviz_screeplot(res.ca) +
28  geom_hline(yintercept=33.33, linetype=2, color="red")
29
30# Color by cos2 values: quality on the factor map
31fviz_ca_row(res.ca, col.row = "cos2",
32            gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), 
33            repel = TRUE)
34
35fviz_ca_col(res.ca, col.col = "cos2",
36            gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), 
37            repel = TRUE)
38# Change the transparency by cos2 values
39fviz_ca_row(res.ca, alpha.row="cos2")
40row <- get_ca_row(res.ca)
41col<-get_ca_col(res.ca)
42row$cos2
43col$cos2
44
45corrplot(row$cos2, is.corr=FALSE)
46corrplot(col$cos2, is.corr=FALSE)
47

اگر مطلب بالا برای شما مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

بر اساس رای ۷ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

آرمان ری بد (+)

«آرمان ری‌بد» دکتری آمار در شاخه آمار ریاضی دارد. از علاقمندی‌های او، یادگیری ماشین، خوشه‌بندی و داده‌کاوی است و در حال حاضر نوشتارهای مربوط به آمار و یادگیری ماشین را در مجله فرادرس تهیه می‌کند.