ضریب همبستگی (Correlation Coefficients) و شیوه‌ محاسبه — به زبان ساده

در تحلیل‌های چند متغیره آماری، شیوه‌های مختلف محاسباتی برای اندازه‌گیری وابستگی یا ارتباط بین دو متغیر تصادفی وجود دارد. منظور از ضریب همبستگی بین دو متغیر، قابلیت پیش‌بینی مقدار یکی برحسب دیگری است. برای مثال، عرضه و تقاضا دو پدیده وابسته به یکدیگر هستند. یکی از روش‌های نمایش ارتباط بین دو متغیر، محاسبه «کوواریانس» (Covariance) و یا «ضرایب همبستگی» (Correlation Coefficient) بین آن‌ها است.

هر چه مقدار این دو شاخص بزرگتر باشد، نشان‌دهنده ارتباط یا وابستگی بیشتر بین دو متغیر است. برای مثال می‌توان وابستگی زیادی بین دو متغیر میزان مصرف برق و دمای هوا در نظر گرفت. زیرا هر چه دما افزایش یابد، استفاده از وسایل سرمایشی نیز افزایش داشته و مصرف برق را بالا می‌برد. در نتیجه وابستگی زیادی بین این دو متغیر وجود دارد.

البته باید توجه داشت که کوواریانس یا همبستگی بیانگر ارتباط علت و معلولی نیستند، بلکه فقط معیاری برای نشان دادن میزان وابستگی بین دو متغیر محسوب می‌شوند.

به عنوان پیش‌زمینه این بحث احتیاج به میانگین‌گیری و محاسبه واریانس دارید. برای آشنایی بیشتر با این مباحث می‌توانید مطالب رابطه بین میانگین حسابی، هندسی و همساز و اندازه‌های پراکندگی — به زبان ساده را مطالعه کنید.

ضریب همبستگی و کوواریانس

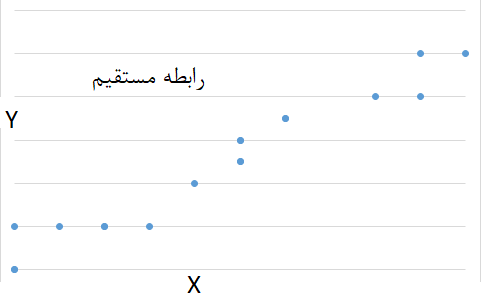
یک روش برای نشان دادن ارتباط بین دو متغیر، استفاده از «کوواریانس» (Covariance) است. این میزان جهت ارتباط بین دو متغیر را نیز نشان می‌دهد. به این معنی که اگر مقدار کوواریانس مثبت شود،‌ بیانگر ارتباط مستقیم بین دو متغیر است. این گفته بدان معناست که با افزایش یکی دیگری نیز افزایش می‌یابد.

فیلم آموزش محاسبات آماری در اکسل Excel

اینجا کلیک کنید

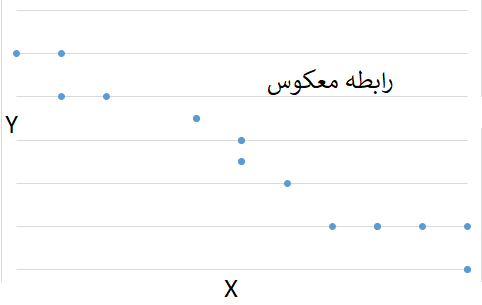
همچنین منفی بودن کوواریانس نشان می‌دهد که جهت تغییرات دو متغیر عکس یکدیگر هستند. به بیان دیگر ارتباط معکوس بین دو متغیر نشان می‌دهد که با افزایش یکی، دیگری کاهش می‌یابد.

فرض کنید X و Y‌ دو متغیر تصادفی با امید-ریاضی $$E(X)$$ و $$E(Y)$$ هستند. رابطه زیر نحوه محاسبه کوواریانس X و Y را که به صورت $$COV(X,Y)$$ نشان می‌دهیم، مشخص کرده است:

$$\large COV(X,Y)=E[(X-E(X))(Y-E(Y))]$$

خواص کوواریانس

با توجه به رابطه تعریف شده برای کوواریانس می‌توان خصوصیات زیر را برایش مشخص کرد:

• تقارن: کوواریانس یک شاخص متقارن است. یعنی $$COV(X,Y)=COV(Y,X)$$.
• واحد ترکیبی: واحد اندازه‌گیری کوواریانس، ترکیبی است. به این معنی که اگر X با واحد متر و Y با واحد کیلوگرم اندازه‌گیری شده باشد، واحد اندازه‌گیری کوواریانس به صورت متر در کیلوگرم است.
• کوواریانس بین X و X برابر با واریانس خواهد بود. $$COV(X,X)=V(X)$$
• اگر بین X و Y رابطه خطی وجود داشته باشد، یعنی داشته باشیم a+bX=Y آنگاه $$COV(X,Y)=bV(X)$$ به این معنی که تغییر مکان داده‌ها در مقدار کوواریانس تاثیری نداشته و فقط تغییر مقیاس باعث می‌شود که کوواریانس نیز به همان مقیاس تبدیل شود.
• با توجه به مقیاس اندازه‌گیری داده‌ها، بزرگی یا کوچکی کوواریانس برای مقایسه مناسب نیست.

مثال 1

براساس مطالعه قد و وزن ۹ نوزاد و نوپا، داده‌های زوجی ($$x,y$$) در جدول زیر ثبت شده‌اند. کوواریانس بین قد و وزن این افراد برابر است با 10.80 کیلوگرم در سانتی‌متر.

میانگین وزن‌ها برابر 6.6 کیلوگرم و میانگین قدها نیز برابر با 62.4 سانتی‌متر است. محاسبات مورد نیاز برای بدست آوردن کوواریانس نیز در جدول زیر قرار دارد.

این مقدار نشان می‌دهد که رابطه مستقیم بین قد و وزن کودکان وجود دارد.

ماتریس کوواریانس

اگر لازم باشد ارتباط بین چندین متغیر، محاسبه و نمایش داده شود، از ماتریس کوواریانس استفاده می‌شود. در سطرها و ستون‌های این ماتریس متغیرها قرار گرفته و مقدارهای درون ماتریس نیز، کوواریانس مربوط به متغیر سطر با ستون متناظرش را نشان می‌دهد. اگر X,Y,Z سه متغیر تصادفی باشند، ماتریس کوواریانس آن‌ها به صورت زیر نمایش داده می‌شود.

$$\large V = \begin{bmatrix} COV(X,X) & COV(X,Y) &COV(X,Z) \\ COV(Y,X)&COV(Y,Y)& COV(Y,Z)\\ COV(Z,X)& COV(Z,Y)& COV(Z,Z) \end{bmatrix}$$

از آنجایی کوواریانس هر متغیر با خودش برابر با واریانس آن متغیر است، گاهی به V ماتریس واریانس-کوواریانس نیز می‌گویند. توجه داشته باشید که ماتریس V یک ماتریس متقارن است و عناصر روی قطر اصلی همان واریانس‌ها هستند.

محاسبه ضرایب همبستگی

همانطور که اشاره شد، کوواریانس به واحد اندازه‌گیری داده‌ها بستگی دارد. در نتیجه نمی‌توان بزرگی کوواریانس دو متغیر را با بزرگی کوواریانس دو متغیر دیگر بدون در نظر گرفتن واحد اندازه‌گیریشان، مقایسه کرد. ضریب همبستگی که شاخصی بدون واحد است، این مشکل را حل کرده.

فیلم آموزش منوی Test نرم افزار آماری MedCalc (رایگان)

اینجا کلیک کنید

در قسمت‌های قبل متوجه شدیم که ضریب همبستگی نیز برای اندازه‌گیری میزان وابستگی بین دو متغیر استفاده می‌شود. با توجه به نوع داده‌ها، شیوه‌های مختلفی برای اندازه‌گیری ضریب همبستگی وجود دارد. اغلب ضریب همبستگی، رابطه بین مقدارهای میانگین دو متغیر را نشان می‌دهد. ضریب همبستگی را با $$\rho$$ و یا r نشان می‌دهند. در این متن به بررسی و شیوه محاسبه «ضریب همبستگی پیرسون» (Pearson Correlation Coefficient) ، «ضریب همبستگی اسپیرمن» (Spearman Correlation Coefficient) و «ضریب همبستگی کندال» (Kendall Correlation Coefficient) می‌پردازیم.

ضریب همبستگی پیرسون

یکی از مشهورترین شیوه‌های اندازه‌گیری وابستگی بین دو متغیر کمی، محاسبه ضریب همبستگی پیرسون است. این شاخص توسط «کارل پیرسون» (Karl Pearson) آماردان انگلیسی در سال‌ 1900 طی مقاله‌ای معرفی شد. او از این شاخص برای بررسی علمی روی علوم زیستی و حتی جمعیتی استفاده کرد و به نتایج جالب توجهی رسید. شیوه محاسبه برای ضریب همبستگی پیرسون در ادامه دیده می‌شود.

فرض کنید X و Y‌ دو متغیر تصادفی هستند که دارای امید-ریاضی $$E(X)$$ و $$E(Y)$$ و واریانس $$V(X)$$ و $$V(Y)$$‌ هستند. ضریب همبستگی بین X و Y‌ را با $$\rho (X,Y)$$ یا $$corr(X<Y)$$ نشان داده و به صورت زیر محاسبه می‌کنیم.

$$\large  \rho(X,Y)=corr(X,Y)=\dfrac{E[(X-E(X))(Y-E(Y))]}{[V(X)V(Y)]^\tfrac{1}{2}}$$

صورت این کسر همان کوواریانس بین دو متغیر X و Y محسوب می‌شود. منظور از E‌ نیز، امید-ریاضی دو متغیر تصادفی X و Y است.

البته باید توجه داشت که ضریب همبستگی پیرسون فقط زمانی که واریانس و امید-ریاضی وجود داشته باشند، قابل محاسبه است. برای مثال داده‌هایی «توزیع کوشی» (Cauchy Distribution) دارای میانگین و واریانس نیستند در نتیجه ضریب همبستگی به این شکل برای آن‌ها قابل محاسبه نیست. همچنین اگر یکی از واریانس‌ها نیز صفر باشد (یعنی داده‌ها پراکندگی نداشته باشند) مقدار ضریب همبستگی نامفهوم خواهد بود.

با استفاده از نامساوی کوشی-شوارتز نیز می‌توان نشان داد که قدر مطلق ضریب همبستگی هرگز بزرگتر از ۱ نخواهد بود. پس می‌توان نوشت:

$$\large -1\leq \rho(X,Y) \leq 1$$

خصوصیات ضریب همبستگی پیرسون

با توجه به تعریفی که ضریب همبستگی پیرسون دارد می‌توان خصوصیات زیر را برای آن اثبات کرد.

• بدون واحد بودن: ضریب همبستگی پیرسون به واحد اندازه‌گیری داده‌ها بستگی ندارد. یعنی شاخصی بدون واحد است. حتی گاهی آن را به صورت درصدی نیز بیان می‌کنند.
• تقارن ضریب همبستگی پیرسون: واضح است که ضریب همبستگی پیرسون دارای تقارن است. زیرا $$COV(X,Y)=COV(Y,X)$$
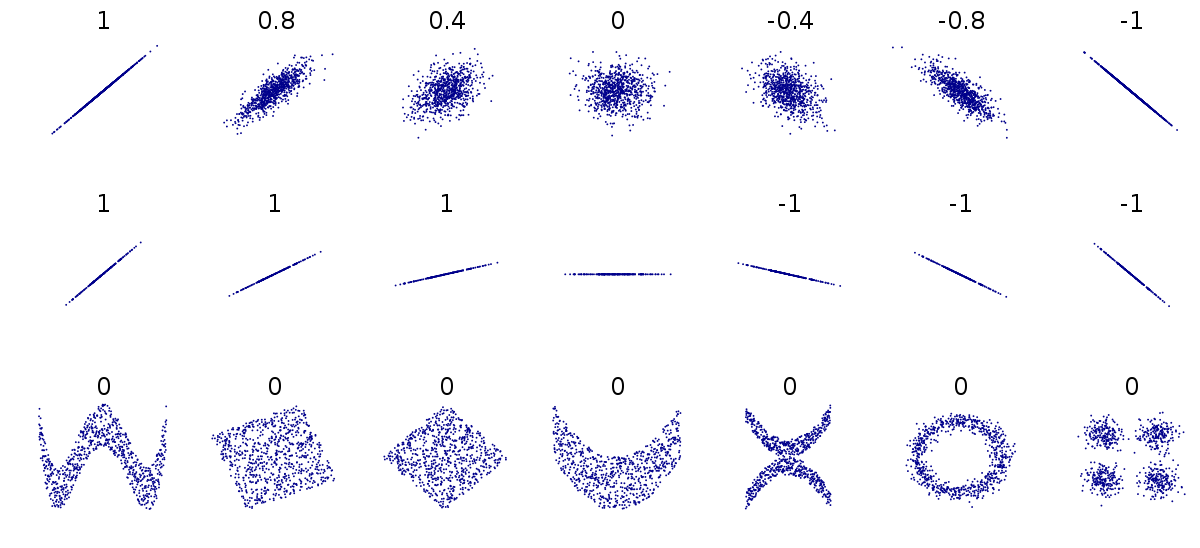
• اندازه‌گیری ارتباط خطی بین دو متغیر: هر چه مقدار ضریب همبستگی به ۱ یا ۱- نزدیک شود، وجود رابطه خطی بین دو متغیر بیشتر می‌شود. فرض کنید a+bX=Y باشد. ضریب همبستگی بین X , Y به صورت زیر قابل محاسبه است:

$$\large  \rho(X,Y)=\dfrac{E[(X-E(X))(a+bX-(a-bE(X))]}{[V(X)b^2V(X)]^\tfrac{1}{2}}$$

حال سعی می‌کنیم صورت کسر ضریب همبستگیرا ساده کنیم.

$$\large E[(X-E(X))(a+bX-(a+bE(X))]=$$

$$\large E[(aX+bX^2-aX-bXE(X)-E(X)a-E(X)bX+E(X)a+bE^2(X)]=$$

$$\large E[bX^2-2bXE(X)+bE^2(X)]=b(E[X^2-2E(X)+E^2(X)]=bE[(X-E(X)]^2=bV(X)$$

از طرفی نیز برای واریانس داریم:

$$\large V(X)V(Y)=V(X)V(a+bX)=V(X)b^2V(X)=b^2V^2(X)$$

در نتیجه برای ضریب همبستگی بین X و Y خواهیم داشت:

$$\large \rho(X,Y)=\dfrac{bV(X)}{[b^2V^2(X)]^\tfrac{1}{2}}=1$$

البته همین محاسبات را برای a-bX=Y نیز می‌توان انجام داد و نتیجه گرفت که ضریب همبستگی پیرسون برای چنین رابطه خطی برابر با ۱- است.

• تعیین جهت همبستگی: چنانچه ضریب همبستگی مثبت باشد، رابطه بین دو متغیر را مستقیم و اگر منفی باشد، رابطه بین دو متغیر معکوس خواهد بود.
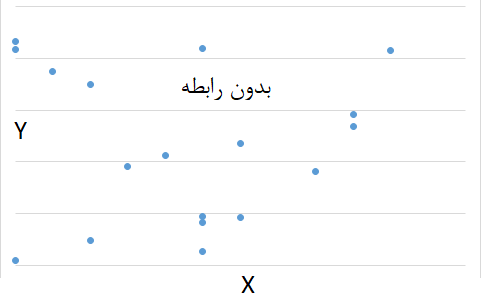
• استقلال دو متغیر: اگر دو متغیر مستقل باشند، ضریب همبستگی پیرسون برابر با صفر خواهد بود. البته عکس این موضوع صحیح نیست. یعنی ممکن است ضریب همبستگی پیرسون برای دو متغیر برابر با صفر باشد در حالیکه آن دو متغیر مستقل نیستند. در چنین حالتی اگر X یک متغیر تصادفی متقارن حول صفر باشد (یعنی $$E(X)=E(X^3)=0$$) و متغیر تصادفی y به صورت $$Y=X^2$$ باشد، آنگاه ضریب همبستگی بین این دو برابر صفر است ولی مشخص است که Y کاملا به X‌ وابستگی دارد. در چنین حالتی صورت مربوط به محاسبه ضریب همبستگی پیرسون به شکل زیر خواهد بود:

$$\large E[(X-E(X))(X^2-E(X^2))]=E[(X-0)(X^2-E(X^2)]=$$

$$\large E(X(X^2-E(X^2))]=E[(X^3)-XE(X^2)]=$$

$$\large E(X^3)-E(X)E(X^2)=0-0=0$$

در نتیجه برای دو متغیر X و Y که به شدت به هم مرتبط هستند ضریب همبستگی برابر با صفر خواهد بود.

• استقلال برای دو متغیر نرمال: اگر دو متغیر X و Y‌ دارای توزیع نرمال باشند، آنگاه صفر بودن ضریب همبستگی می‌تواند دلیلی برای استقلال دو متغیر تصادفی نرمال باشد.
• ضریب همبستگی نمونه‌ای: اگر یک نمونه تصادفی به حجم n از متغیرهای تصادفی X و Y‌ به صورت $$(x_i,y_i)$$‌ داشته باشیم، «ضریب همبستگی نمونه‌ای پیرسون» (Pearson Sample Correlation Coefficient) به شکل زیر محاسبه می‌شود:

$$\large r(x,y)=\dfrac{n\sum x_iy_i-\sum x_i \sum y_i}{[n\sum x^2_i-(\sum x_i)^2]^\tfrac{1}{2}[n\sum y^2_i-(\sum y_i)^2]^\tfrac{1}{2}}$$

مثال ۲

براساس داده‌های موجود در جدول مربوط به مثال ۱ ضریب همبستگی پیرسون به صورت زیر قابل محاسبه است. این اطلاعات در جدول محاسبه شده‌اند.

ضریب همبستگی رتبه‌ای اسپیرمن

با توجه به اینکه ضریب همبستگی پیرسون براساس میانگین و واریانس محاسبه می‌شود، ممکن است در مقابل داده‌های دورافتاده، منحرف شده و میزان همبستگی را به درستی نشان ندهد. در چنین مواقعی از ضریب همبستگی رتبه‌ای اسپیرمن استفاده می‌شود. همبستگی رتبه‌ای اسپیرمن به مانند ضریب پیرسون، نشان می‌دهد تمایل یک متغیر به پیروی کردن از مقدارهای متغیر دیگر چقدر است.

فیلم آموزش نرم افزار MedCalc برای تجزیه و تحلیل و انجام محاسبات آماری

اینجا کلیک کنید

این شاخص همبستگی توسط «چارلز اسپیرمن» (Charles Spearman) دانشمند روانشناس انگلیسی در سال 1904 معرفی شد. او با استفاده از این ضریب همبستگی توانست تئوری‌هایش در زمینه شناخت و هوش را توسعه دهد.

در این ضریب همبستگی به جای محاسبه روی مقدارها، از رتبه‌ها استفاده می‌شود. به همین دلیل به آن ضریب همبستگی رتبه‌ای می‌گویند. بنابراین اگر $$rx_1,rx_2,\ldots,rx_n$$ رتبه‌های مربوط به مقدارهای $$x_1,x_2,\ldots,x_n$$ و $$ry_1,ry_2,\ldots,ry_n$$ رتبه‌های مربوط به مقدارهای $$y_1,y_2,\ldots,y_n$$ باشد ضریب همبستگی رتبه‌ای اسپیرمن که به صورت $$r_s$$ نشان داده می‌شود طبق رابطه زیر قابل محاسبه است:

$$\large r_s(x,y)=\dfrac{cov(r_x,r_y)}{s_{rx}.s_{ry}}$$

مشخص است که در ضریب همبستگی رتبه‌ای اسپیرمن، اساس رتبه‌ها هستند، نه خود مقدارها. همچنین ضریب همبستگی اسپیرمن شدت رابطه خطی را اندازه‌گیری نمی‌کند. به این معنی که ممکن است ضریب همبستگی رتبه‌ای اسپیرمن برابر ۱ باشد در حالی که رابطه خطی بین دو متغیر وجود نداشته باشد.

مثال ۳

برای داده‌های زوجی $$(0,1), (10,100),(101,500),(102,2000)$$ مقدار ضریب همبستگی اسپیرمن برابر است با ۱ در حالیکه نمودار ترسیمی، رابطه خطی را نشان نمی‌دهد و ضریب همبستگی پیرسن برابر است با 0.754.

ضریب هماهنگی کندال

ضریب هماهنگی کندال نیز مانند ضریب همبستگی اسپیرمن، به جای مقدار از ترتیب مقدارها برای اندازه‌گیری میزان وابستگی استفاده می‌کند. این شاخص توسط «موریس کندال» (Maurice Kendall) دانشمند انگلیسی علم آمار در سال 1938 معرفی شد. او بوسیله این شاخص، میزان همخوانی رتبه‌ها را اندازه‌گیری کرد.

فرض کنید زوج‌های $$(x_1,y_1), (x_2,y_2),\ldots,(x_n,y_n)$$ مشاهدات متغیرهای X و Y را تشکیل می‌دهند. زوج $$(x_i,y_i)$$ و $$(x_j,y_j)$$ را «هماهنگ» (Concordant) می‌گویند اگر $$x_i<x_j$$‌ داشته باشیم $$y_i<y_j$$. به بیان دیگر اگر داده‌های این زوج‌ها را براساس مولفه اول یا دوم مرتب کنیم،‌ دارای رتبه‌های یکسانی خواهند بود. در حالت عکس این زوج‌ها را «ناهماهنگ» (Discordant) می‌نامند.

حال براساس تعریف هماهنگ و ناهماهنگ برای زوج‌ها، اگر تعداد زوج‌های هماهنگ را با $$|Con|$$ و تعداد زوج‌های ناهماهنگ را نیز با $$|Dis|$$ نشان دهیم، ضریب هماهنگی کندال به صورت زیر محاسبه می‌شود:

$$\large \tau= \dfrac{|Con|-|Dis|}{n(n-1)/2}$$

خصوصیات ضریب هماهنگی کندال

• از آنجایی که مخرج این کسر تعداد انتخاب‌های زوج‌ها از بین n مشاهده است، همیشه از صورت بزرگتر است. پس ضریب همبستگی کندال از ۱ کوچکتر و از ۱- بزرگتر است.
• اگر همه زوج‌ها با هم هماهنگ باشند مقدار ضریب هماهنگی کندال برابر است با ۱.
• اگر همه زوج‌ها ناهماهنگ باشند ضریب هماهنگی کندال برابر است با ۱-.
• اگر X و Y‌ مستقل باشند، انتظار داریم که ضریب هماهنگی کندال نیز برابر با ۰ باشد.

شکل دیگری نیز برای محاسبه ضریب هماهنگی کندال وجود دارد که از تابع علامت یا sgn استفاده می‌کند. منظور از $$sgn(x)$$ علامت x است. اگر علامت x مثبت باشد،‌ مقدار sgn برابر با ۱ و اگر منفی باشد sgn برابر با ۱- است. در حالتی که x صفر باشد، مقدار sgn صفر در نظر گرفته می‌شود. به این ترتیب رابطه محاسباتی برای ضریب هماهنگی کندال به صورت زیر است:

$$\large \tau =\dfrac {2}{n(n-1)}\sum _{i<j}sgn(x_{i}-x_{j})sgn(y_{i}-y_{j})$$

مثال ۴

برای داده‌های مثال ۱ محاسبات مربوط به ضریب همبستگی اسپیرمن و کندال در جدول زیر آورده شده است.

برای مثال، زوج اول یعنی $$(1,1)$$ نسبت به همه زوج‌های دیگر هماهنگ است پس میزان هماهنگی این زوج برابر با ۸ و برای زوج دوم درجه هماهنگی ۷ و ... است. در نتیجه مجموع تعداد هماهنگی‌ها برابر ۳۶ می‌شود.

معرفی فیلم آموزش همبستگی و رگرسیون خطی در SPSS

رابطه بین متغیرها، بوسیله ضریب‌های همبستگی تعیین شده و مدل سازی نیز به کمک تکنیک رگرسیون امکان‌پذیر است. به کمک شاخص‌های مربوطه همبستگی قادر به کشف میزان رابطه بین متغیرها هستیم. ولی برای نشان دادن مدل رابطه بین متغیرها از یک روش آماری به نام رگرسیون خطی در SPSS استفاده می کنیم، تا شکل رابطه‌ بین متغیرها به زبان آماری نوشته شود. در این آموزش، روش کمترین مربعات خطا برای پیدا کردن پارامترهای مدل خطی به کار رفته و فرامین در محیط SPSS اجرا می‌شوند. در این بین نیز آزمون‌های مربوط به مدل و تعیین صحت آن مطرح و راهکارهای برطرف کردن بعضی از مشکلات نیز گفته می‌شود. این آموزش شامل ۲ ساعت محتوای ویدیویی است که طبق سرفصل زیر ارائه شده است.

• درس اول: همبستگی و رابطه بین دو متغیر، رابطه خطی مستقیم و معکوس، ضریب همبستگی پیرسون- Correlation Coeficient، آزمون مربوط به ضریب همبستگی پیرسون- Pearson Correlation Coefficient، ضریب همبستگی جزئی- Partial Correlation
• درس دوم: معادله خط برگشت Regression، متغیر مستقل و وابسته، فرضیات مربوط به شیوه محاسبه ضرایب رگرسیونی، فرض مربوط به نرمال بودن باقی مانده ها، فرض مربوط به ثابت بودن واریانس باقی مانده ها، فرض مربوط به تصادفی بودن باقی مانده ها، تعیین معادله خط رگرسیون با یک متغیر مستقل (برآورد ضرایب رگرسیون)، آزمون های تعیین صحت مدل رگرسیون (Regression model)، تحلیل باقی مانده ها.
• درس سوم: رگرسیون چند گانه، تعیین معادله خط رگرسیون با چند متغیر، آزمون های تعیین صحت مدل رگرسیونی، روش های کاهش تعداد متغیرهای مستقل (روش Backward-Forward-Stepwise)، بررسی شرایط مربوط به متغیرهای مستقل.
• درس چهارم: رگرسیون و مدل های قابل تبدیل به مدل خطی.

این آموزش برای دانشجویان رشته‌های آمار- مهندسی و داده کاوی وعلم داده مناسب است.

فیلم آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS

اینجا کلیک کنید

اگر مطلب بالا برای‌تان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش همبستگی و رگرسیون خطی در SPSS
• رابطه بین میانگین حسابی، هندسی و همساز
• اندازه‌های پراکندگی — به زبان ساده
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• متغیر تصادفی، تابع احتمال و تابع توزیع احتمال
• توزیع نرمال و توزیع نرمال استاندارد — به زبان ساده
• ضرایب همبستگی و ماتریس همبستگی در R — کاربرد در یادگیری ماشین

^^