ماتریس درهم ریختگی (Confusion Matrix) – از صفر تا صد
پیش از این، در مطالبی با عناوین «روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای بیرونی (External Index)» و «روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای درونی (Internal Index)»، به روشهای ارزیابی مدلهای خوشهبندی و نتایج حاصل از آنها پرداخته شد. در این مطلب، «ماتریس درهم ریختگی» که روشی برای ارزیابی نتایج دستهبندی است، پرداخته خواهد شد.

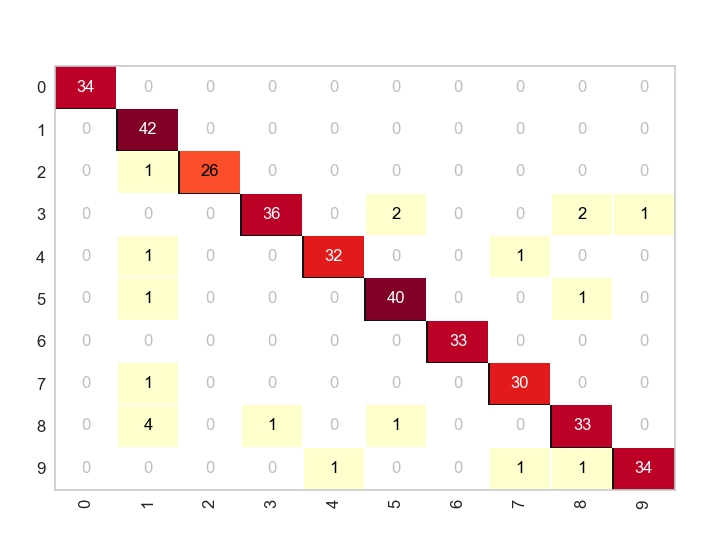
ماتریس درهم ریختگی
در بحث «دستهبندی» (Classification) یک «مجموعه داده» (Data Set) با استفاده از روشهای دستهبندی، هدف دستیابی به بالاترین دقت و صحت ممکن در دستهبندی و تشخیص دستهها است. در برخی از مسائل، تشخیص صحیح نمونههای مربوط به یکی از دستهها برای ما اهمیت بیشتری دارد. به عنوان مثال، تحقیقی را در نظر بگیرید که در آن، هدف شناسایی افراد مبتلا به یک نوع خاص از یک بیماری خطرناک است. فرض کنید برای افرادی که مبتلا به این بیماری هستند، خطر مرگ وجود دارد و جهت رفع این خطر، نیاز به دریافت نوعی داروی خاص دارند. در این شرایط، تشخیص درست بیماران دارای اهمیت بسیار زیادی است.
به این معنا که خطا در تشخیص افراد سالم قابل چشم پوشی است اما برای شناسایی افراد بیمار نمیتوان این احتمال را به جان خرید. به عبارت دیگر، انتظار ما تشخیص تمام افراد بیمار است، بدون جا انداختن، حتی اگر فرد سالمی به اشتباه جز افراد بیمار دستهبندی شود. در چنین مواقعی، که دقت و صحت تشخیص یک دسته در مقایسه با دقت و صحت تشخیص کلی، اهمیت بیشتری دارد، مفهوم «ماتریس درهمریختگی» (Confusion Matrix)، به کمک ما میآید.
بر اساس مثالی که پیشتر بیان شد، فرض کنید تعلق به دسته افراد بیمار را مثبت بودن (Positive) و عدم تعلق به این دسته را منفی بودن (Negative) در نظر بگیریم. هر نمونه یا فردی در واقعیت، متعلق به یکی از کلاسهای مثبت یا منفی است و از سوی دیگر، از هر الگوریتمی که برای دستهبندی دادهها استفاده شود، در نهایت هر نمونه عضو یکی از این دو «دسته» (Class) دستهبندی خواهد شد. بنابراین برای هر نمونه داده، یکی از چهار حالتی که در ادامه بیان شده، ممکن است اتفاق بیفتد.
- نمونه عضو دسته مثبت باشد و عضو همین کلاس تشخیص داده شود (مثبت صحیح یا True Positive)
- نمونه عضو کلاس مثبت باشد و عضو کلاس منفی تشخیص داده شود (منفی کاذب یا False Negative)
- نمونه عضو کلاس منفی باشد و عضو همین کلاس تشخیص داده شود (منفی صحیح یا True Negative)
- و در نهایت، نمونه عضو کلاس منفی باشد و عضو کلاس مثبت تشخیص داده شود (مثبت کاذب یا False Positive)
پس از اجرای الگوریتم دستهبندی، با توجه به توضیحات و تعاریف ذکر شده، میتوان عملکرد یک طبقهبند را به کمک جدولی به شکل زیر بررسی کرد.
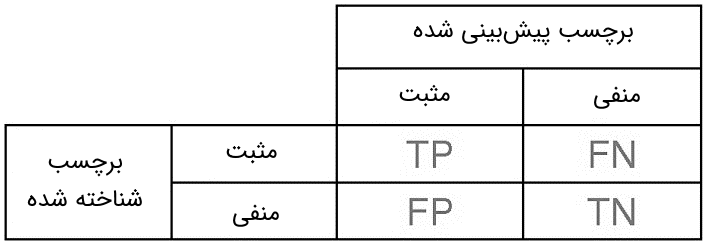
این جدول را اصطلاحا ماتریس درهم ریختگی میگویند. جدول یا ماتریس درهم ریختگی، نتایج حاصل از طبقهبندی را بر اساس اطلاعات واقعی موجود، نمایش میدهد. حال بر اساس این مقادیر میتوان معیارهای مختلف ارزیابی دسته بند و اندازهگیری دقت را تعریف کرد.
پارامتر صحت (Accuracy)، متداولترین، اساسیترین و سادهترین معیار اندازهگیری کیفیت یک دستهبند است و عبارت است از میزان تشخیص صحیح دستهبند در مجموع دو دسته. این پارامتر در واقع نشانگر میزان الگوهایی است که درست تشخیص داده شدهاند و بر اساس ماتریس ارائه شده در بالا، به شکل زیر فرموله و تعریف میشود:
Accuracy = (TP+TN) / (TP+FN+FP+TN)
البته، پارامتر صحت معمولا به صورت درصد بیان میشود. اما پارامترهای دیگری نیز علاوه بر معیار صحت وجود دارند که میتوان به سادگی از این ماتریس استخراج کرد. یکی از متداولترین آنها، معیار حساسیت (Sensitivity) است که آن را «نرخ پاسخهای مثبت درست» (True Positive Rate) نیز میگویند. حساسیت به معنی نسبتی از موارد مثبت است که آزمایش آنها را به درستی به عنوان نمونه مثبت تشخیص داده است. این پارامتر به صورت زیر محاسبه میشود:
Sensitivity (TPR) =TP / (TP+FN)
در واقع، «حساسیت» همان معیار بحث شده در مورد مثال بالا است. معیاری که مشخص میکند دستهبند، به چه اندازه در تشخیص تمام افراد مبتلا به بیماری موفق بودهاست. همانگونه که از رابطه فوق مشخص است، تعداد افراد سالمی که توسط دستهبند به اشتباه به عنوان فرد بیمار تشخیص داده شدهاند، هیچ تاثیری در محاسبه این پارامتر ندارد و در واقع زمانی که پژوشهگر از این پارامتر به عنوان پارامتر ارزیابی برای دستهبند خود استفاده میکند، هدفش دستیابی به نهایت صحت در تشخیص نمونههای کلاس مثبت است.
در نقطه مقابل این پارامتر، ممکن است در مواقعی صحت تشخیص کلاس منفی حائز اهمیت باشد. از متداولترین پارامترها که معمولا در کنار حساسیت بررسی میشود، پارامتر خاصیت (Specificity)، است که به آن «نرخ پاسخهای منفی درست» (True Negative Rate) نیز میگویند. خاصیت به معنی نسبتی از موارد منفی است که آزمایش آنها را به درستی به عنوان نمونه منفی تشخیص داده است. این پارامتر به صورت زیر محاسبه میشود:
Specificity (TNR) = TN / (TN+FP)
این دو پارامتر (حساسیت و خاصیت) نیز مشابه معیار صحت، معمولا به صورت درصد بیان میشوند. واضح است که پیشبینی عالی، پیشبینی است که مقادیر Sensitivity و Specificity مربوط به آن، هر دو صد درصد باشند؛ اما احتمال وقوع این اتفاق در واقعیت بسیار کم است و همیشه یک حداقل خطایی وجود دارد. پارامترهای حساسیت و خاصیت، بنابر ماهیتی که دارند همواره در رقابت با یکدیگر هستند. یعنی افزایش یکی با کاهش دیگری همراه است و برعکس. همین وضعیت منجر به تولید ابزاری دیگر برای ارزیابی کیفیت دستهبندها شده است. «منحنی مشخصه عملکرد سیستم» (Receiver Operating Characteristic | ROC)، عبارت است از منحنی که ارتباط بین دو پارامتر حساسیت و خاصیت را بیان میکند.
چنانکه در شکل زیر مشاهده میکنید، محور عمودی این نمودار نشاندهنده نرخ مثبت صحیح (Sensitivity)، و محور افقی نشاندهنده مقدار نرخ مثبت غلط () است. نتایج مختلف دستهبندی نشانگر نقاط مختلف بر روی این نمودار هستند و در نهایت یک منحنی را تشکیل میدهند. با توجه به شکل زیر، در بهترین حالت و با فرض طبقهبندی صد درصد صحیح در هر دو دسته، نقطه مربوطه عبارت است از نقطه گوشه بالای سمت چپ، یعنی نقطه (0,1) و نیز با فرض دستهبندی به صورت تصادفی، نقطه متناظر در منحنی، یکی از نقاط موجود روی خط واصل نقطه (0,0) و نقطه (1,1) خواهد بود. در واقعیت، منحنی حاصل از یک دستهبندی، منحنی بین این دو حالت است.
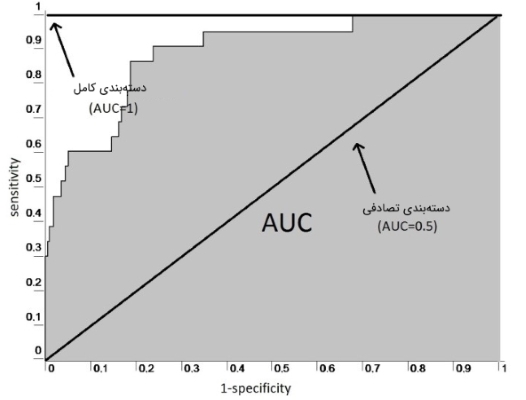
مساحت زیر این نمودار (Area Under Curve)، به عنوان یک معیار برای ارزیابی عملکرد دستهبند مورد استفاده قرار میگیرد. با توجه به توضیحاتی که پیشتر ارائه شد، بدیهی است که در حالت ایدهآل، مساحت زیر منحنی برابر با بیشترین مقدار خود، یعنی یک است. بنابراین، هر چه مساحت زیر نمودار به عدد یک نزدیکتر باشد، به معنای بهتر بودن عملکرد دستهبند است. علاوه بر دو پارامتر حساسیت و خاصیت، پارامترهای دیگری هم از ماتریس درهمریختگی استخراج میشوند که هر یک بیان کننده مفهومی هستند و کاربردهای متفاوتی دارند.
از جمله آنها، دو پارامتر مقدار پیشبینی شده مثبت (Positive Prediction Value) و مقدار پیشبینی شده منفی (Negative Predictive Values) هستند، که برای بیان «نسبت پاسخهای درست در هر دسته» استفاده میشوند. ارزش اخباری مثبت، بیان کننده این است که چند درصد از الگوهایی که دستهبند آنها را مثبت تشخیص داده، در واقعیت هم مثبت هستند و به همین ترتیب، ارزش اخباری منفی نشان میدهد که چند درصد از نمونههایی که عضو دسته منفی تشخیص داده شدهاند، در واقعیت هم عضو همین دسته هستند. این دو پارامتر نیز به سادگی از روی ماتریس درهمریختگی به شکل زیر فرمولبندی میشوند:
PPV=TP / (TP+FP)
NPV=TN / (TN+FN)
پارامتر مهم دیگری به نام «معیار اف» (F-Measure) وجود دارد که برای ارزیابی عملکرد دستهبندها بسیار مورد استفاده قرار میگیرد و از ترکیب دو پارامتر حساسیت و ارزش اخباری مثبت حاصل میشود. با این توضیح که پارامتر ارزش اخباری مثبت را اصطلاحا دقت (Precision)، و حساسیت را اصطلاحا یادآوری (Recall | صحت) مینامند، «معیار اف» به صورت زیر تعریف میشود:
F-measure= 2 * (Recall * Precision) / (Recall + Precision)
ماتریس درهم ریختگی، با وجود منطق و ساختار ساده ای که دارد، مفهومی قدرتمند است که در انواع تحقیقات، میتواند به تنهایی اطلاعاتی جامع از نحوه عملکرد دستهبند ارائه کند.
این مطلب توسط نویسنده مهمان «مینا خوشرنگباف» نوشته شده است.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دادهکاوی و یادگیری ماشین
- آموزش دادهکاوی (Data Mining) در متلب
- مجموعه آموزشهای آمار و احتمالات
- دادهکاوی (Data Mining) — از صفر تا صد
- یادگیری علم داده (Data Science) با پایتون — از صفر تا صد
- تقلبنامه (Cheat Sheet) ارزیابی مدل در یادگیری ماشین — راهنمای سریع و کامل
- ارزیابی مدل یادگیری عمیق — به زبان ساده
- معیار ارزیابی BIC در مدلهای احتمالی — از صفر تا صد
^^













«مقدار نرخ مثبت غلط (One-Specificity) است.» در ترجمه احتمالاً متوجه نشدن که (1-Specificity) منظور «یک منهای خاصیت» است.
اگر مشکل راستچین بودن متن هم هست، در خواندن واضح نیست.
با سلام،
اصلاح موردنظر انجام شد.
با تشکر از همراهی شما با مجله فرادرس
نه درسته! ایراد از برداشت من بود!
“نمونه عضو کلاس مثبت باشد و عضو کلاس منفی تشخیص داده شود (منفی کاذب یا False Negative)”
این عبارت نیاز به بازبینی دارد …
False Positive درسته
و همچنین تعریف متضادش در همان پاراگراف
توضیحات اولیه خوب بود اما این نوشته صفر تا صد نبود چون به طور مثال گفته نشده که چطور از روی یک سری داده ها باید ماتریس درهم ریختگی رو شکل بدیم؟ و سوال بعدی اینکه اگر داده های ما به صورت سیگنال باشه آیا باید حتما به داده خام تبدیل کنیم (اگر بله چطوری؟) و بعد روی ماتریس درهم ریختگی ببریم یا اینکه همینطوری از روی سیگنال هم میشه این ماتریس رو شکل داد؟
لطفا در رابطه با این 2 سوال هم پاسخ بدید ممنون میشم.
سلام ..عالی بود..فقط کد برنامه نویسی با متلب این قسمت هم بگذارید ممنون
عالیییی بود