جریان تراکم‌ پذیر (Compressible Flow) — اصول و مفاهیم

در حالت کلی و در علم مکانیک، مایعات و گازها را در دسته سیالات (Fluids) قرار می‌دهند. جریان‌های تراکم ناپذیر با مفهوم ثابت ماندن چگالی در زمان و مکان در ارتباط هستند. از دیدگاه تئوری تحلیل فیزیک سیال تراکم‌پذیر مشکل‌تر از سیال تراکم ناپذیر است. در واقعیت مفهوم تراکم ناپذیری را می‌توان برای اکثر مایعات در نظر گرفت چرا که با اعمال فشار روی آن‌ها چگالیشان تغییر نخواهند کرد.

بررسی گازها از دیدگاه ترمودینامیکی

در جریاناتی که دارای سرعت بالایی هستند، عبارت v²/2 به اندازه‌ای بزرگ است که دیگر خواص سیال را تحت تاثیر قرار می‌دهد. جریان‌های تراکم‌پذیر از دیدگاه آنتروپی و انرژی مورد بررسی قرار می‌گیرند. در حقیقت مطالعه مفهوم تراکم‌پذیری در علم ترمودینامیک و مکانیک سیالات قرار می‌گیرد.

گاز کامل

یک گاز به سیستمی از ذرات اتلاق می‌شود که به دلیل نیروهای بین مولکولی، ذرات آن دارای حرکاتی تصادفی هستند. این نیروها وابسته به فاصله بین مولکولی آنها است که منجر به تغییر رفتار گاز می‌شود. توجه داشته باشید که علم ترمودینامیک رفتار مجموعه‌ای از ذرات را مورد بررسی قرار می‌دهد. در حقیقت این علم، گاز را به صورت ماکروسکوپیک مطالعه می‌کند.

در شرایط دمایی و فشاری که گاز به صورت تراکم‌پذیر است، مشاهده شده که میانگین فاصله بین مولکولی بیشتر از قطر مولکول‌ها است [حدود ۱۰ برابر است]. بنابراین تمامی خواص جریان، به صورت ماکروسکوپیک قابل بیان است. در حالت کلی رابطه بین خواص در یک گاز کامل را می‌توان به شکل زیر بیان کرد:

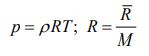
در این رابطه M، وزن مولکولی گاز و R ثابت گازها در نظر گرفته می‌شود که برای گازهای مختلف متفاوت است. هم‌چنین $$\bar R$$ عددی ثابت و برابر با $$8314 \enspace {J \over kg.K}$$ است. برای گاز کاملی که پتانسیل مبادله انرژی با محیط دارد، روابط ترمودینامیکی زیر را  می‌توان نوشت:

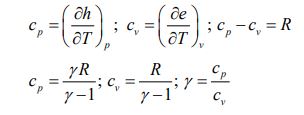
در معادلات بالا پارامترهای Cp ،Cv ،γ ،h ،e به ترتیب برابر با انرژی داخلی، آنتالپی ویژه، ضریب اتمیسیته، گرمای ویژه در حجم ثابت و گرمای ویژه در فشار ثابت هستند.

قانون اول ترمودینامیک

یک سیستم به مجموعه جرمی از گاز اتلاق می‌شود که توسط مرزی از اطرافش جدا شده است. مبادله حرارت و کار با سیستم مذکور منجر به تغییر انرژی کل آن می‌شود. زمانی که سیستمی در حالت پایا باشد، تغییرات انرژی کل سیستم را می‌توان با استفاده از قانون اول ترمودینامیک و به صورت زیر بیان کرد:

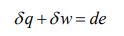
برای تغییر دیفرانسیلی de، بینهایت مسیر به منظور انتقال کار و گرما به سیستم وجود دارد. در حالت کلی سه فرآیند اصلی آدیاباتیک، برگشت‌پذیر و آیزنتروپیک را می‌توان برای سیستم تعریف کرد.

قانون دوم ترمودینامیک

به منظور پیش بینی جهت یک فرآیند ترمودینامیکی، خاصیت جدیدی تحت عنوان آنتروپی تعریف می‌شود. تغییر آنتروپی یک سیستم که ناشی از انتقال حرارت جزئی dq باشد، برابر با حاصل جمع dq/T و افزایش آنتروپی ناشی از برگشت‌ناپذیری‌های سیستم است. بنابراین برای چنین فرآیندی می‌توان تغییر جزئی آنتروپی را به شکل زیر بیان کرد:

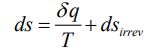
از آنجایی که برگشت‌ناپذیری‌ها همواره منجر به افزایش آنتروپی سیستم می‌شوند بنابراین می‌توان گفت نامساوی زیر در یک فرآیند برگشت‌ناپذیر بایستی برقرار باشد.

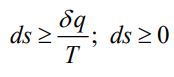
معادله ۳ و ۴ بیان‌های متفاوت قانون دوم ترمودینامیک هستند. به‌منظور محاسبه تغییرات آنتروپی یک فرآیند ترمودینامیکی، دو رابطه را می‌توان از معادلات ارائه شده در بالا استخراج کرد.

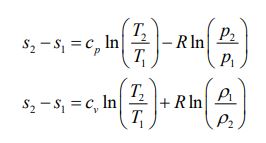
فرآیند آیزنتروپیک، به فرآیندی اتلاق می‌شود که در آن تغییری در آنتروپی کل سیستم وجود نداشته باشد. در حقیقت چنین فرآیندی، برگشت‌پذیر و آدیاباتیک در نظر گرفته می‌شود. هنگامی که گاز کاملی فرآیندی آیزنتروپیک را تجربه می‌کند، تغییرات فشار، دما و چگالی را می‌توان با استفاده از رابطه زیر به هم ارتباط داد.

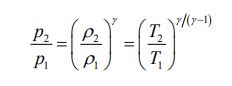
خاصیت‌های مهم جریان تراکم‌پذیر

به‌طور ساده می‌توان گفت، جریان تراکم‌پذیر عبارت است از جریانی که در آن چگالی متغیر باشد. در حالت کلی این تغییرات بسیار در فشار و دما است که منجر به تراکم‌پذیری سیال می‌شود. از این رو، با توجه به معادله برنولی، فشار سیال متحرک نیز متغیر خواهد بود.

قبل از توضیح و بدست آوردن معادلات مربوط به جریان تراکم‌پذیر، تعدادی از پارامترهای مرتبط با این نوع از جریان را معرفی می‌کنیم.

مدول بالک ($$E_{\nu}$$)

این خاصیت توصیف کننده میزان تغییرات چگالی سیال در حالتی است که دما ثابت و فشار متغیر باشد. در حقیقت، مدول بالک توصیف کننده تغییرات چگالی نسبت به فشار است. از دیدگاه ریاضیاتی این خاصیت به صورت زیر تعریف می‌شود.

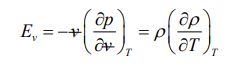
ضریب انبساط حجمی ($$\beta$$)

این ضریب بیان‌کننده میزان تغییرات چگالی نسبت به دما است. بنابراین این خاصیت تاثیرات تغییر فشار سیال در چگالی آن را مورد توجه قرار نمی‌دهد. ضریب انبساط حجمی را می‌توان به صورت زیر تعریف کرد.

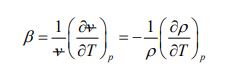
تراکم‌پذیری ($$\kappa$$)

ضریب تراکم‌پذیری نشان می‌دهد که با تغییر فشار سیال، چگالی آن به چه میزان تغییر می‌کند. سوال:

با توجه به تعریف ارائه شده در بالا، به نظر شما ضریب تراکم‌پذیری برای مایعات نزدیک به چه عددی است؟

ضریب تراکم‌پذیری $$\kappa$$ (کاپا) به شکل زیر تعریف می‌شود.

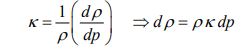
معادلات اصلی برای جریان تراکم‌پذیر

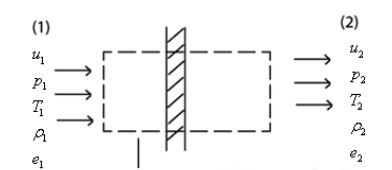
مطابق با شکل زیر جریان تراکم‌پذیری را در نظر بگیرید که درون حجم کنترلی مستطیلی شکل، عبور می‌کند.

برای چنین سیستمی معادله پیوستگی را می‌توان به شکل زیر نوشت.

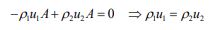
جریان به صورت یک بعدی فرض می‌شود. بنابراین هنگام عبور آن از حجم کنترل، کمیت‌های مرتبط با جریان مثل سرعت (u)، فشار (p)، دما(T)، چگالی ($$\rho$$) و انرژی داخلی، تغییر می‌کنند. به‌منظور نوشتن معادلات فرضیات زیر در نظر گرفته شده است.

• جریان در سمت چپ و راست حجم کنترل به صورت یکنواخت در نظر گرفته شده.
• مساحتِ هر دو طرف حجم کنترل با یکدیگر برابر است.
• جریان غیر لزج و پایا است؛ هم‌چنین از نیروهای حجمی صرف نظر شده.
• هیچ مبادله انرژی و یا کار با حجم کنترل صورت نمی‌گیرد.

معادلات پایستگی جرم، مومنتوم و انرژی برای این سیستم به شکل زیر بیان می‌شوند:

پایستگی جرم:

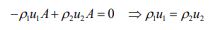
پایستگی مومنتوم:

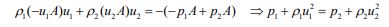
پایستگی انرژی:

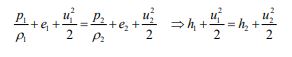
همچنین خاصیتی را تحت عنوان آنتالپی، برابر با $$h=e+{p \over {\rho}}$$ تعریف می‌کنیم.

انتقال موج در یک محیط تراکم‌پذیر

در بالا، معادلات اصلی را برای سیال تراکم‌پذیر بیان کردیم. در این قسمت قصد داریم تا با استفاده از این معادلات، جریان تراکم‌پذیر را توصیف کنیم.

با توجه به معادله پایستگی جرم می‌توان سرعت موج صوتی  را در محیط انتشارش یافت. برای این منظور، مطابق با شکل زیر، گازی را فرض کنید که به صورت ساکن در یک استوانه قرار گرفته است.

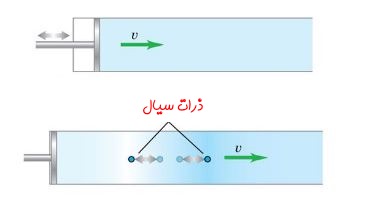
سیستم در حالت تعادل ترمودینامیکی خود قرار دارد؛ از طرفی می‌توان فرض کرد که گاز مفروض از بینهایت لایه تشکیل شده. این جمله به این معناست که لایه‌های قرار گرفته درون سیلندر، حضور پیستون را حس نمی‌کنند.

در این لحظه پیستون به اندازه‌ای بسیار اندک به سمت راست حرکت داده می‌شود. در این زمان لایه‌ چسبیده به پیستون به اندازه اندکی فشرده شده و دیگر لایه‌های گاز این تغییر را (در لحظه اولیه) حس نمی‌کنند. با گذشت زمان دیگر لایه‌های گاز نیز به تدریج از حرکت پیستون مطلع می‌شوند. [در حقیقت مطلع شدن به معنای فشرده شدن آنها است.] بنابراین با گذشت زمان خبر به حرکت در آمدن پیستون در کل سیال منتقل می‌شود. این باخبر شدن توسط «موج صوتی» اتفاق می‌افتد. همانطور که اسم آن پیدا است، سرعت انتقال این موج برابر با سرعت صوت است.

اجازه دهید سرعت انتقال اطلاعات (یا همان سرعت موج صوتی) را بدست آوریم. در ابتدا فرض کنید که پیستون ساکن است. ناگهان آن را با سرعتِ جزئی dV به حرکت در می‌آوریم. در این حالت موجی صوتی با سرعت a در گاز ایجاد می‌شود. تغییر اندک سرعت پیستون منجر به تغییر در چگالی و فشار هوای جلوی آن می‌شود.

در این حالت به‌منظور تحلیل سیستم راحت‌تر این است که موج را ساکن فرض کنیم. از این رو تمامی سرعت‌های موجود در مسئله را با a- جمع می‌کنیم [از مفهوم نسبی بودن سرعت استفاده شده است]. در دو تصویر زیر این معادل‌سازی انجام شده است.

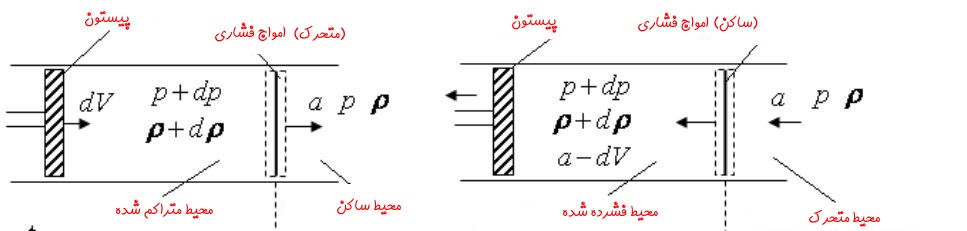
شکل سمت راست را در نظر بگیرید. در آن موج ساکن را به عنوان حجم کنترل در نظر گرفته و معادلات ارائه شده در بالا را برای آن‌ می‌نویسیم.

معادله پیوستگی (یا همان بقای جرم)

نرخ جریان عبوری از مرزهای حجم کنترل پایسته است، از این رو می‌توان گفت:

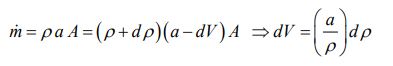
معادله بالا، دبی جریان در چپ و راست حجم کنترل را نشان می‌دهد.

بقای مومنتوم

از آنجایی که ضخامت (در راستای محور x) مرزهای موج صوتی بسیار اندک است، می‌توان از حضور نیروهای برشی قرار گرفته بر روی حجم کنترل - در مقابل نیروی فشاری وارد به آن - صرف نظر کرد. با این فرضیات معادله بقای مومنتوم برای این سیستم به صورت زیر قابل بیان است.

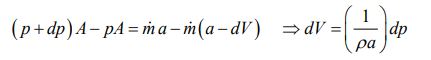
معادله انرژی

از آنجایی که ضخامت موج بسیار نازک است و سرعت آن نیز بسیار زیاد، می‌توان از انتقال حرارت صورت گرفته با آن صرف نظر کرد؛ از این رو فرآیند ترمودینامیکی مفروض به صورت آدیاباتیک در نظر گرفته می‌شود. با فرض آدیاباتیک بودن فرآیند، معادله پایستگی انرژی برای این موج صوتی را می‌توان به شکل زیر نوشت:

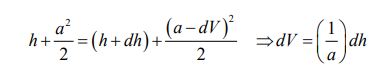
معادله آنتروپی

به‌منظور تعیین جهت فرآیند ترمودینامیکی بایستی تغییرات آنتروپی را بیابیم. با برابر قرار دادن سمت راست دو معادله بالا به رابطه زیر می‌رسیم.

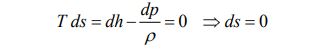
بنابراین از آنجایی که تغییرات آنتروپی برابر با صفر است، فرآیند مفروض اتفاق خواهد افتاد. با برابر قرار دادن سمت راست معادلات پیوستگی و مومنتوم که اندکی بالاتر بیان شدند، می‌توان سرعت صوت را در قالب معادله زیر یافت.

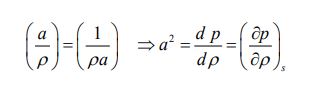
اندیس s نشان دهنده آیزنتروپیک بودن فرآیند است. توجه داشته باشید که برای یک فرآیند آیزنتروپیک رابطه زیر میان چگالی و فشار برقرار است.

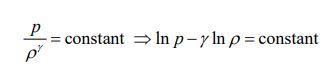
با مشتق‌گیری از معادله بالا و اعمال قانون گاز کامل (p=ρRT)، سرعت صوت را می‌توان به شکل زیر محاسبه کرد.

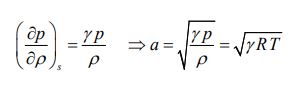
عدد ماخ

همان‌طور که از فرمول بالا نیز می‌توان دید، سرعت صوت خاصیتی ترمودینامیکی است که مقدار آن در نقاط مختلف، متفاوت است. زمانی که جریانی با سرعتی بسیار بالا روی جسم صلبی عبور کند، اثر تراکم‌پذیری سیال بسیار مشهود است. نرخ سرعت محلی (V) به سرعت صوت را عدد ماخ می‌نامند. بنابراین این عدد به شکل زیر قابل بیان است.

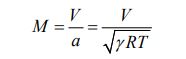
عدد ماخ را می‌توان در قالب گذاره‌های زیر تفسیر کرد.

۱. عدد ماخ معیاری از میزان تراکم‌پذیری سیال است. برای نمونه جریانی که ماخ آن کمتر از ۰.۳ باشد،‌ تراکم‌ناپذیر در نظر گرفته می‌شود.

۲. می‌توان نشان داد که عدد ماخ معادل با نسبت انرژی جنبشی به انرژی درونی است. در معادله زیر این تفسیر اثبات شده.

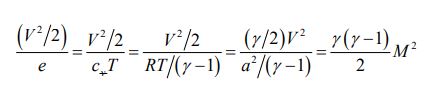
۳. عدد ماخ نشان دهنده نسبت انرژی جنبشی گاز به انرژی تصادفی مولکول‌های تشکیل دهنده آن است.

رژیم جریان تراکم‌پذیر

به‌منظور توضیح رژیم جریان تراکم‌پذیر، بهتر است جریانی را تصور کنیم که حول جسمی آیرودینامیکی جریان دارد. در شکل زیر چنین وضعیتی را در ماخ‌های مختلف نشان داده.

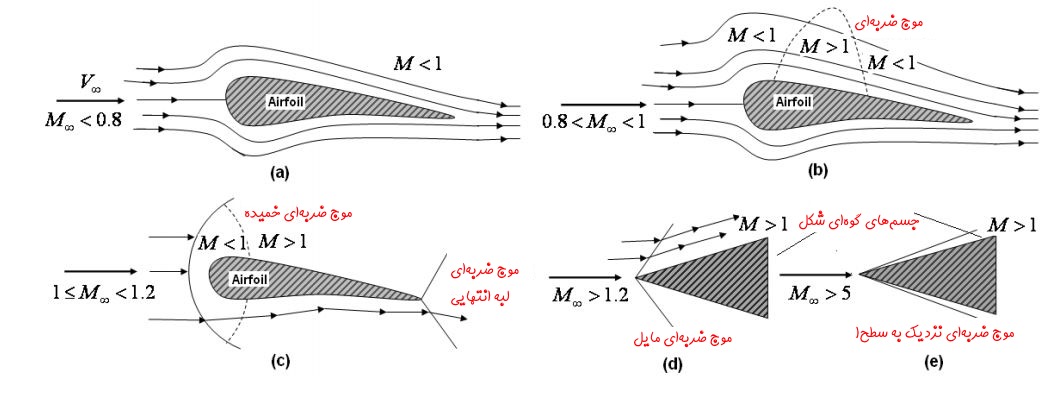
سرعت و سرعت صوتِ جریان در دور دست برابر با _∞V و _∞a هستند. بنابراین عدد ماخِ جریان در دوردست برابر با $$M_{\infty}={V_\infty \over a_{\infty}}$$ است. خطوط جریان عبوری روی جسم را می‌توان رسم کرد.

بنابراین عدد ماخ محلی در نقطه‌های متفاوت، با یکدیگر فرق دارند. در ادامه رژیم‌های نشان داده شده در تصویر بالا را شرح خواهیم داد.

جریان زیرصوتی

جریان زیر صوت زمانی اتفاق می‌افتد که ماخ جریان ورودی به جسم در تمامی مکان‌ها کمتر از ۱ باشد. در این حالت خطوط جریان سیال به صورت کاملا مجزا و منظم هستند. هم‌چنین در این حالت خواص جریان به شکلی کاملا پیوسته تغییر می‌کنند.

در دوردست خطوط جریان به صورت مستقیم هستند، در حالی که با نزدیک شدن آن‌ها به جسم به تدریج منحرف می‌شوند. در نتیجه در هنگام عبور جریان روی جسم، گاز منبسط شده و سرعتش افزایش می‌یابد. در نتیجه در بالای جسم آیرودینامیکی، سرعت جریان بیشتر از سرعت جریان آزاد است. به علاوه عدد ماخ محلی در سطح ایرفویل، در زمانی که ماخ جریان آزاد به اندازه کافی کمتر از یک باشد، روی ایرفویل نیز کمتر از ۱ باقی می‌ماند.

جریان گذرصوتی

اگر ماخ جریان آزاد همچنان کمتر از ۱ بماند اما نزدیک به این عدد باشد، در بعضی از نقاط سطح آیرودینامیکی، ممکن است ماخ جریان بیشتر از ۱ شود. بنابراین کل جریان به صورت ترکیبی از ماخ بیشتر و کم‌تر از ۱ خواهد بود. به چنین جریانی «گذر صوتی» گفته می‌شود.

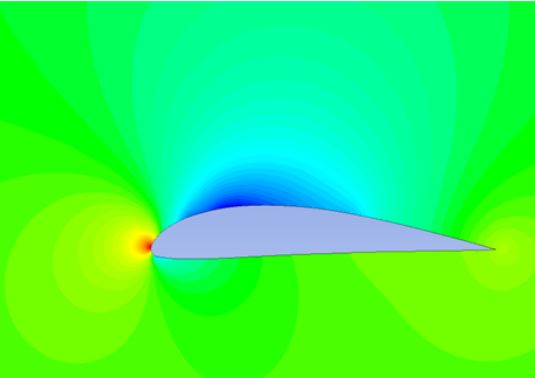
در حقیقت این جریان زمانی ایجاد می‌شود که ماخ جریان به طور ناگهانی و به میزانی اندک، بیشتر از ۱ شود. در این حالت موجی تحت عنوان «موج ضربه‌ای» (Shock Wave) تشکیل شده که منجر به تغییر ناگهانی خواص سیال در دو طرفش می‌شود. دو نوعِ معروفِ امواج ضربه‌ای، موج عمود و موج مایل هستند. مهم‌ترین مشخصه این امواج تغییر ناگهانی و شدید خواص سیال هستند. شکل زیر کانتور عدد ماخ برای یک جریان گذرصوتی را نشان می‌دهد.

جریان فراصوت

اگر در تمامی دامنه، ماخ جریان بیشتر از ‍۱ باشد، به جریان مذکور فراصوت گفته می‌شود. به‌ منظور کاهش نیروی درگِ اجسام آیرودینامیکی، تمامی آن‌ها را با لبه تیز طراحی می‌کنند. در شکل زیر نمونه‌ای از موج ضربه‌ای تشکیل شده در هنگام عبور جریان فراصوت روی یک جسم آیرودینامیکی نشان داده شده است.

جریان مافوق‌ صوت

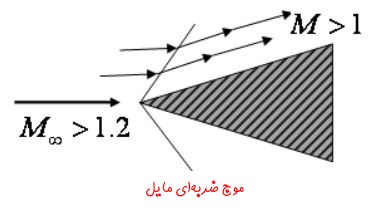
زمانی که ماخ جریان آزاد از حالت فراصوت نیز بیشتر باشد، موج ضربه‌ای مایل، به سطح جسم آیرودینامیکی نزدیک‌تر خواهد شد. شکل زیر این وضعیت را نشان داده است.

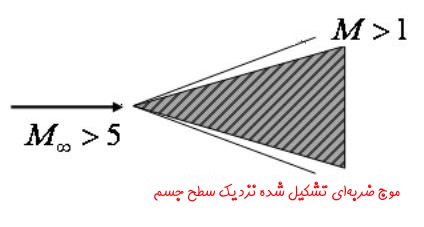
در این حالت مقادیر چگالی، فشار و دما در اطراف موج ضربه‌ای تشکیل‌شده، به شدت افزایش خواهند یافت. از این رو فضای بین موج ضربه‌ای و جسم به اندازه‌ای داغ می‌شود که گاز را یونیزه می‌کند. انیمیشن زیر جسمی را نشان می‌دهد که با سرعت مافوق صوت در حال حرکت است. ماخ این ذره برابر با ۵ است. جالب است بدانید که در چنین حالتی جسم از موج صوتی ایجاد شده توسط خودش، پیش می‌افتد. در انیمیشن زیر می‌بینید که چگونه ذره، از موج صوتی ایجاد شده توسط خودش جلو افتاده است.

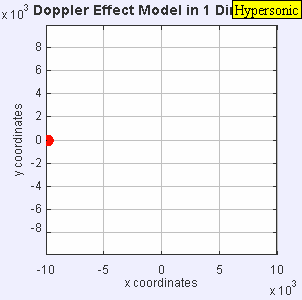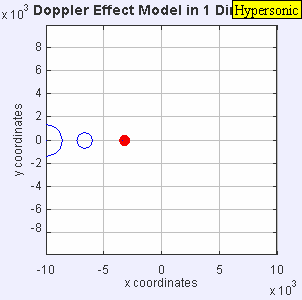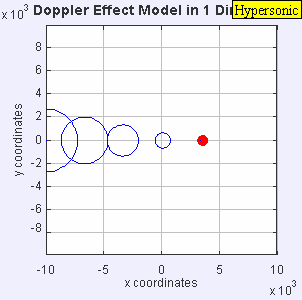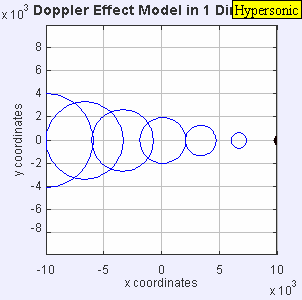
در عمل دیده شده که شرایط فراصوت زمانی اتفاق می‌افتد که ماخ جریان آزاد بیشتر از ۵ باشد. جالب است بدانید که اگر هواپیمایی با سرعت مافوق صوت از کنار شما عبور کند در ابتدا خود هواپیما را می‌بینید و سپس صدای آن را می‌شنوید! نکته دیگر در مباحث مرتبط با صوت، اثر دوپلر است که در مطلب «اثر دوپلر (Doppler Effect) — به زبان ساده» به صورت دقیق به آن پرداخته شده است.

نهایتا رژیم‌های جریان تراکم‌پذیر را می‌توان به ترتیب زیر دسته‌بندی کرد.

پدیده موج ضربه‌ای مفهومی بسیار مهم و پیچیده در آیرودینامیک است که در طراحی اجسام پرنده بسیار تاثیرگذار است. در بخشی به طور مجزا در مورد این پدیده بحث خواهیم کرد.