کلون کردن درخت دودویی با اشاره گرهای تصادفی — راهنمای کاربردی

در این مطلب، چگونگی «کلون کردن درخت دودویی با اشاره گرهای تصادفی» (Clone a Binary Tree with Random Pointers) بیان و پیاده‌سازی آن در زبان برنامه‌نویسی ++C انجام شده است. در اینجا، منظور از کلون کردن در واقع کپی کردن است.

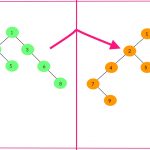
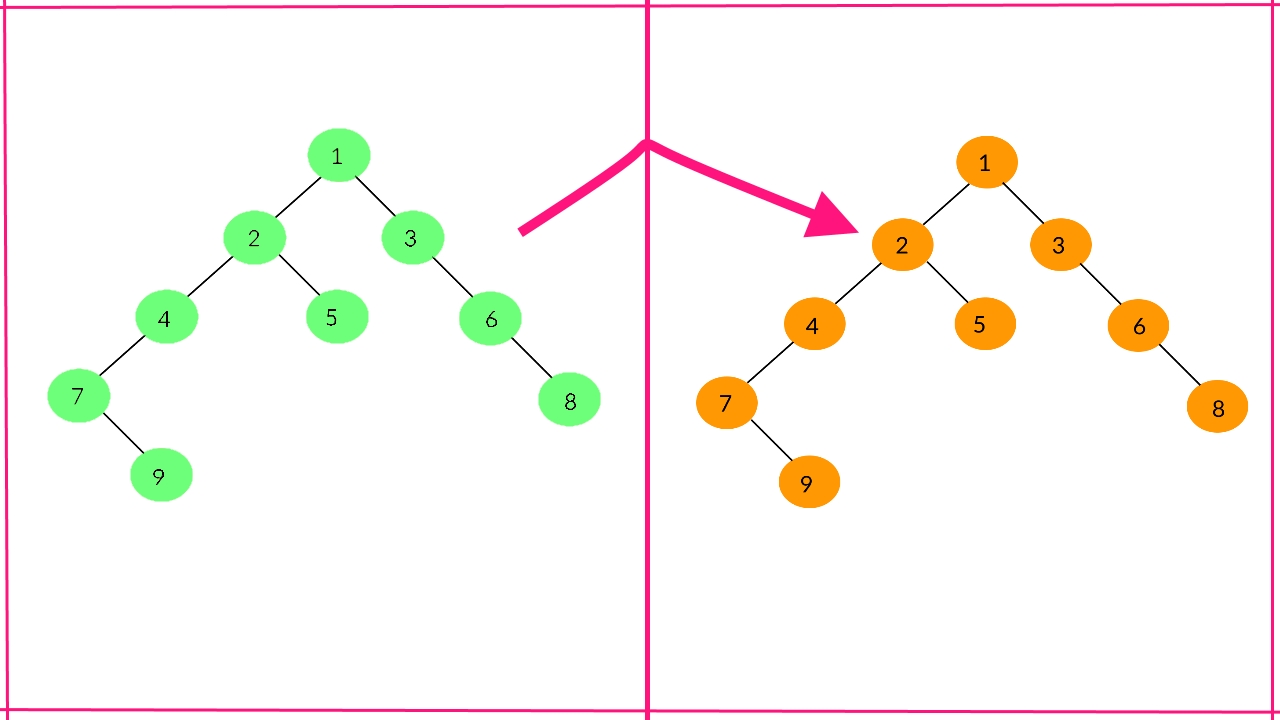
کلون کردن درخت دودویی با اشاره گرهای تصادفی

یک «درخت دودویی» (Binary Tree) داده شده که در آن هر «گره» (Node)، دارای ساختار زیر است.

struct node {  
    int key; 
    struct node *left,*right,*random;
}

اشاره‌گر تصادفی به هر گره تصادفی از درخت دودویی اشاره دارد و حتی می‌تواند به Null نیز اشاره و درخت دودویی داده شده را کلون کند.

روش ۱: استفاده از درهم‌سازی

ایده نهفته در پس روش استفاده از «درهم‌سازی» (Hash) آن است که نگاشت گره‌های درخت داده شده را در «جدول هش» (Hashtable) ذخیره کند. در ادامه، گام‌های انجام این کار همراه با جزئیات بیان شده‌اند.

فیلم آموزش مروری بر توابع Hash و خطر تصادم در آن ها (رایگان) در فرادرس

کلیک کنید

۱. به صورت بازگشتی، درخت دودویی داده شده را پیمایش و مقادیر کلید، اشاره گر چپ و اشاره گر راست را برای کلون کردن درخت کپی کن. در حین کپی، نگاشت را از گره درخت داده شده به گره درخت کلون شده در جدول هش ذخیره کن. در شبه کد زیر، «cloneNode» گره کنونی مشاهده شده از درخت کلون و «treeNode» گره کنونی مشاهده شده از درخت داده شده است.

 cloneNode->key = treeNode->key
cloneNode->left = treeNode->left
cloneNode->right = treeNode->right
map[treeNode] = cloneNode

۲. به صورت بازگشتی، هر دو درخت را پیمایش کن و نقاط تصادفی را با استفاده از ورودی‌های جدول هش تنظیم کن.

   cloneNode->random = map[treeNode->random] 

در ادامه، پیاده‌سازی ++C ایده بالا، ارائه شده است. پیاده‌سازی که در ادامه آمده از unordered_map از STL استفاده کرده است.

// A hashmap based C++ program to clone a binary  
// tree with random pointers 
#include<iostream> 
#include<unordered_map> 
using namespace std; 
  
/* A binary tree node has data, pointer to left child, 
    a pointer to right child and a pointer to  
    random node*/
struct Node 
{ 
    int key; 
    struct Node* left, *right, *random; 
}; 
  
/* Helper function that allocates a new Node with the 
   given data and NULL left, right and random pointers. */
Node* newNode(int key) 
{ 
    Node* temp = new Node; 
    temp->key = key; 
    temp->random = temp->right = temp->left = NULL; 
    return (temp); 
} 
  
/* Given a binary tree, print its Nodes in inorder*/
void printInorder(Node* node) 
{ 
    if (node == NULL) 
        return; 
  
    /* First recur on left sutree */
    printInorder(node->left); 
  
    /* then print data of Node and its random */
    cout << "[" << node->key << " "; 
    if (node->random == NULL) 
        cout << "NULL], "; 
    else
        cout << node->random->key << "], "; 
  
    /* now recur on right subtree */
    printInorder(node->right); 
} 
  
// This function creates clone by copying key and left and right pointers 
// This function also stores mapping from given tree node to clone. 
Node* copyLeftRightNode(Node* treeNode, unordered_map<Node *, Node *> &mymap) 
{ 
    if (treeNode == NULL) 
        return NULL; 
    Node* cloneNode = newNode(treeNode->key); 
    mymap[treeNode] = cloneNode; 
    cloneNode->left  = copyLeftRightNode(treeNode->left, mymap); 
    cloneNode->right = copyLeftRightNode(treeNode->right, mymap); 
    return cloneNode; 
} 
  
// This function copies random node by using the hashmap built by 
// copyLeftRightNode() 
void copyRandom(Node* treeNode,  Node* cloneNode, unordered_map<Node *, Node *> &mymap) 
{ 
    if (cloneNode == NULL) 
        return; 
    cloneNode->random =  mymap[treeNode->random]; 
    copyRandom(treeNode->left, cloneNode->left, mymap); 
    copyRandom(treeNode->right, cloneNode->right, mymap); 
} 
  
// This function makes the clone of given tree. It mainly uses 
// copyLeftRightNode() and copyRandom() 
Node* cloneTree(Node* tree) 
{ 
    if (tree == NULL) 
        return NULL; 
    unordered_map<Node *, Node *> mymap; 
    Node* newTree = copyLeftRightNode(tree, mymap); 
    copyRandom(tree, newTree, mymap); 
    return newTree; 
} 
  
/* Driver program to test above functions*/
int main() 
{ 
    //Test No 1 
    Node *tree = newNode(1); 
    tree->left = newNode(2); 
    tree->right = newNode(3); 
    tree->left->left = newNode(4); 
    tree->left->right = newNode(5); 
    tree->random = tree->left->right; 
    tree->left->left->random = tree; 
    tree->left->right->random = tree->right; 
  
    //  Test No 2 
    //    tree = NULL; 
  
    //  Test No 3 
    //    tree = newNode(1); 
  
    //  Test No 4 
    /*    tree = newNode(1); 
        tree->left = newNode(2); 
        tree->right = newNode(3); 
        tree->random = tree->right; 
        tree->left->random = tree; 
    */
  
    cout << "Inorder traversal of original binary tree is: \n"; 
    printInorder(tree); 
  
    Node *clone = cloneTree(tree); 
  
    cout << "\n\nInorder traversal of cloned binary tree is: \n"; 
    printInorder(clone); 
  
    return 0; 
}

خروجی قطعه کد بالا، به صورت زیر است.

Inorder traversal of original binary tree is:
[4 1], [2 NULL], [5 3], [1 5], [3 NULL],

Inorder traversal of cloned binary tree is:
[4 1], [2 NULL], [5 3], [1 5], [3 NULL],

روش ۲: ویرایش موقت درخت دودویی داده شده

الگوریتم این روش، در ادامه آمده است.

فیلم آموزش درخت جستجوی دودویی (AVL) در ساختمان داده ها (رایگان) در فرادرس

کلیک کنید

۱. گره‌های جدید را در درخت کلون شده بساز و هر گره جدید را در درخت اصلی، بین لبه اشاره‌گر چپ از گره متناظر درج کن. (مشاهده تصویر زیر، برای درک بهتر این موضوع، توصیه می‌شود.)

اگر کره کنونی A و فرزند سمت چپ آن B است (A — >> B)، گره جدید کلون شده با کلید A ساخته می‌شود (cA) و به عنوان A — >> cA — >> B قرار داده می‌شود (B می‌تواند نال یا فرزند غیر نال سمت چپ باشد). اشاره‌گر فرزند سمت راست به درستی تنظیم می‌شود. اگر برای فرزند کنونی A، فرزند راست در درخت اصلی C است (A — >> C)، سپس، گره‌های کلون شده متناظر cA و cC مشابه cA —- >> cC هستند.

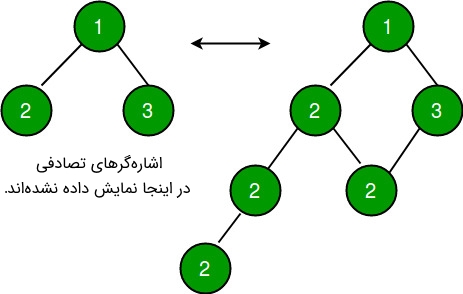
۲. تنظیم اشاره‌گر تصادفی در درخت کلون شده به ازای درخت اصلی.

اگر اشاره‌گر تصادفی A به گره B اشاره کند، در درخت کلون شده، cA به cB اشاره می‌کند (cA و cB گره‌های جدید در درخت کلون شده و متناظر با گره‌های A و B در درخت اصلی هستند).

۳. اشاره‌گرهای سمت چپ را به درستی در درخت اصلی و درخت کلون شده، بازیابی کن.

در ادامه، پیاده‌سازی الگوریتم بالا در  زبان برنامه‌نویسی ++C ارائه شده است.

#include <iostream> 
using namespace std; 
  
/* A binary tree node has data, pointer to left child, a pointer to right 
   child and a pointer to random node*/
struct Node 
{ 
    int key; 
    struct Node* left, *right, *random; 
}; 
  
/* Helper function that allocates a new Node with the 
   given data and NULL left, right and random pointers. */
Node* newNode(int key) 
{ 
    Node* temp = new Node; 
    temp->key = key; 
    temp->random = temp->right = temp->left = NULL; 
    return (temp); 
} 
  
/* Given a binary tree, print its Nodes in inorder*/
void printInorder(Node* node) 
{ 
    if (node == NULL) 
        return; 
  
    /* First recur on left sutree */
    printInorder(node->left); 
  
    /* then print data of Node and its random */
    cout << "[" << node->key << " "; 
    if (node->random == NULL) 
        cout << "NULL], "; 
    else
        cout << node->random->key << "], "; 
  
    /* now recur on right subtree */
    printInorder(node->right); 
} 
  
// This function creates new nodes cloned tree and puts new cloned node 
// in between current node and it's left child 
// i.e. if current node is A and it's left child is B ( A --- >> B ), 
//      then new cloned node with key A wil be created (say cA) and 
//      it will be put as 
//      A --- >> cA --- >> B 
// Here B can be a NULL or a non-NULL left child 
// Right child pointer will be set correctly 
// i.e. if for current node A, right child is C in original tree 
// (A --- >> C) then corresponding cloned nodes cA and cC will like 
// cA ---- >> cC 
Node* copyLeftRightNode(Node* treeNode) 
{ 
    if (treeNode == NULL) 
        return NULL; 
  
    Node* left = treeNode->left; 
    treeNode->left = newNode(treeNode->key); 
    treeNode->left->left = left; 
    if(left != NULL) 
        left->left = copyLeftRightNode(left); 
  
    treeNode->left->right = copyLeftRightNode(treeNode->right); 
    return treeNode->left; 
} 
  
// This function sets random pointer in cloned tree as per original tree 
// i.e. if node A's random pointer points to node B, then 
// in cloned tree, cA wil point to cB (cA and cB are new node in cloned 
// tree corresponding to node A and B in original tree) 
void copyRandomNode(Node* treeNode, Node* cloneNode) 
{ 
    if (treeNode == NULL) 
        return; 
    if(treeNode->random != NULL) 
        cloneNode->random = treeNode->random->left; 
    else
        cloneNode->random = NULL; 
  
    if(treeNode->left != NULL && cloneNode->left != NULL) 
        copyRandomNode(treeNode->left->left, cloneNode->left->left); 
    copyRandomNode(treeNode->right, cloneNode->right); 
} 
  
// This function will restore left pointers correctly in 
// both original and cloned tree 
void restoreTreeLeftNode(Node* treeNode, Node* cloneNode) 
{ 
    if (treeNode == NULL) 
        return; 
    if (cloneNode->left != NULL) 
    { 
        Node* cloneLeft = cloneNode->left->left; 
        treeNode->left = treeNode->left->left; 
        cloneNode->left = cloneLeft; 
    } 
    else
        treeNode->left = NULL; 
  
    restoreTreeLeftNode(treeNode->left, cloneNode->left); 
    restoreTreeLeftNode(treeNode->right, cloneNode->right); 
} 
  
//This function makes the clone of given tree 
Node* cloneTree(Node* treeNode) 
{ 
    if (treeNode == NULL) 
        return NULL; 
    Node* cloneNode = copyLeftRightNode(treeNode); 
    copyRandomNode(treeNode, cloneNode); 
    restoreTreeLeftNode(treeNode, cloneNode); 
    return cloneNode; 
} 
  
  
/* Driver program to test above functions*/
int main() 
{ 
/*  //Test No 1 
    Node *tree = newNode(1); 
    tree->left = newNode(2); 
    tree->right = newNode(3); 
    tree->left->left = newNode(4); 
    tree->left->right = newNode(5); 
    tree->random = tree->left->right; 
    tree->left->left->random = tree; 
    tree->left->right->random = tree->right; 
  
//  Test No 2 
//    Node *tree = NULL; 
/* 
//  Test No 3 
    Node *tree = newNode(1); 
  
//  Test No 4 
    Node *tree = newNode(1); 
    tree->left = newNode(2); 
    tree->right = newNode(3); 
    tree->random = tree->right; 
    tree->left->random = tree; 
  
  Test No 5 
    Node *tree = newNode(1); 
    tree->left = newNode(2); 
    tree->right = newNode(3); 
    tree->left->left = newNode(4); 
    tree->left->right = newNode(5); 
    tree->right->left = newNode(6); 
    tree->right->right = newNode(7); 
    tree->random = tree->left; 
*/
//    Test No 6 
    Node *tree = newNode(10); 
    Node *n2 = newNode(6); 
    Node *n3 = newNode(12); 
    Node *n4 = newNode(5); 
    Node *n5 = newNode(8); 
    Node *n6 = newNode(11); 
    Node *n7 = newNode(13); 
    Node *n8 = newNode(7); 
    Node *n9 = newNode(9); 
    tree->left = n2; 
    tree->right = n3; 
    tree->random = n2; 
    n2->left = n4; 
    n2->right = n5; 
    n2->random = n8; 
    n3->left = n6; 
    n3->right = n7; 
    n3->random = n5; 
    n4->random = n9; 
    n5->left = n8; 
    n5->right = n9; 
    n5->random = tree; 
    n6->random = n9; 
    n9->random = n8; 
  
/*    Test No 7 
    Node *tree = newNode(1); 
    tree->left = newNode(2); 
    tree->right = newNode(3); 
    tree->left->random = tree; 
    tree->right->random = tree->left; 
*/
    cout << "Inorder traversal of original binary tree is: \n"; 
    printInorder(tree); 
  
    Node *clone = cloneTree(tree); 
  
    cout << "\n\nInorder traversal of cloned binary tree is: \n"; 
    printInorder(clone); 
  
    return 0; 
}

خروجی قطعه کد بالا، به صورت زیر است.

Inorder traversal of original binary tree is:
[5 9], [6 7], [7 NULL], [8 10], [9 7], [10 6], [11 9], [12 8], [13 NULL],

Inorder traversal of cloned binary tree is:
[5 9], [6 7], [7 NULL], [8 10], [9 7], [10 6], [11 9], [12 8], [13 NULL],

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده

^^