معادله دایره — به زبان ساده

دایره به منحنی اطلاق می‌شود که فاصله تمامی نقاط آن، از یک نقطه مرجع عددی ثابت باشد. یک دایره دو مشخصه اصلی دارد:

• شعاع
• مرکز

مرکز همان نقطه مرجعی است که در بالا ذکر شد. شعاع نیز برابر با فاصله نقاط منحنی تا مرکز است.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

در شکل زیر دایره،‌ شعاع و مرکز آن نشان داده شده است.

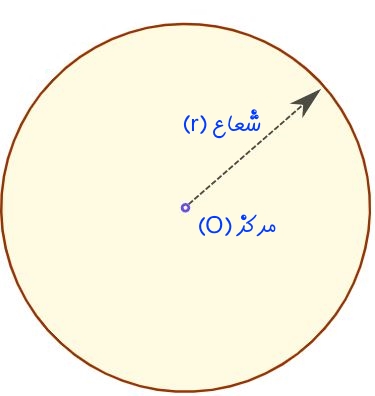
نمودار دایره

شکل زیر، دایره‌ای به شعاع ۵ و مرکز (۰,0) را نشان می‌دهد.

فیلم آموزش ریاضی 3 – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

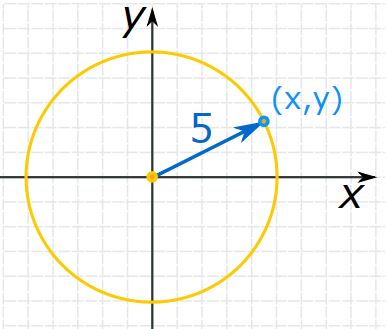
حال می‌خواهیم فاصله نقاط روی منحنی تا مرکز را بررسی کنیم. در حالتی عمومی، مطابق با شکل زیر، مختصاتی برابر با (x,y) را روی منحنی در نظر بگیرید.

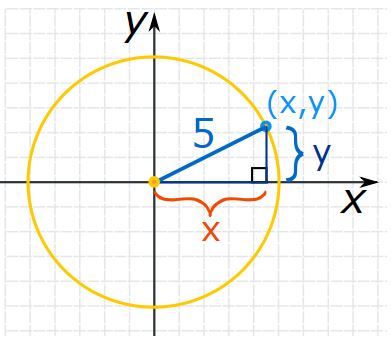
با فرض کردن یک مثلث درون دایره و هم‌چنین با استفاده از قانون فیثاغورس، رابطه زیر را بین مختصات (x,y) می‌توان نوشت:

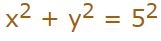
بینهایت نقطه روی دایره وجود دارد که در رابطه بالا صدق می‌کنند. در شکل و جدولِ زیر تعدادی از این نقاط نشان داده شده‌اند.

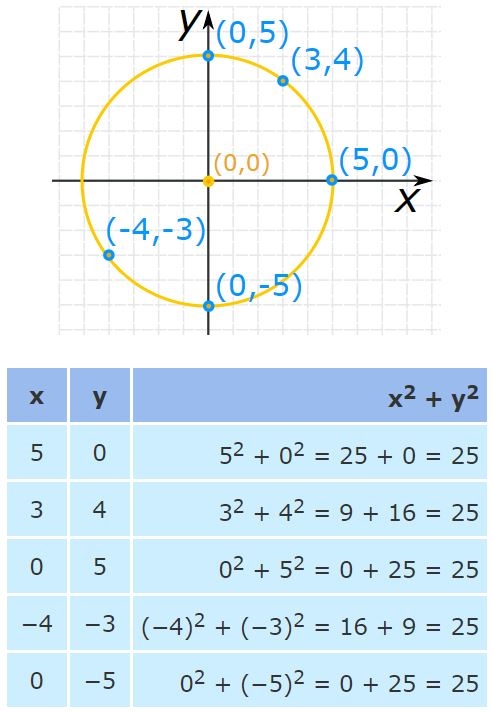
با استفاده از مفهوم بالا می‌توان مختصات یک نقطه مجهول را یافت.

مثال ۱

فرض کنید روی یک دایره به شعاع ۵ و مرکز مختصات (۰,0) ایستاده‌ایم. با فرض این‌که مختصات x این نقطه برابر با ۲ باشد،‌ مختصات y را بدست آورید.

همان‌گونه که بیان شد،‌ رابطه زیر بین مختصات (x,y) چنین دایره‌ای برقرار است.

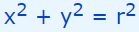
مقدار r در رابطه بالا برابر با ۵ است. هم‌چنین با جایگذاری مقدار x در آن، مختصات y را می‌توان به‌ترتیب زیر بدست آورد.

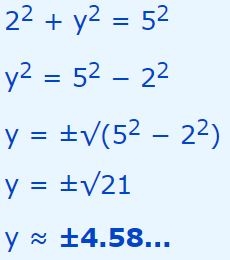
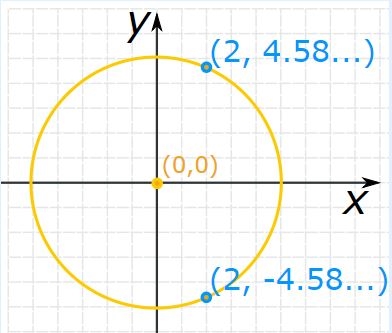
علامت ± نشان دهنده این است که در x=2، دو عدد y وجود دارد. در شکل زیر دو نقطه مفروض نشان داده شده‌اند.

رابطه عمومی دایره

در بالا حالت‌هایی را بیان کردیم که در آن مرکز دایره در مبدأ مختصات قرار داشت.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

به نظر شما در حالتی که مرکز دایره در مختصات (a,b) باشد، رابطه بین x,y به چه شکل خواهد بود؟

جهت پاسخ به سوال بالا،‌ مطابق با شکل زیر حالتی را در نظر بگیرید که در آن مرکز یک دایره به شعاع r، در نقطه (a,b) قرار دارد.

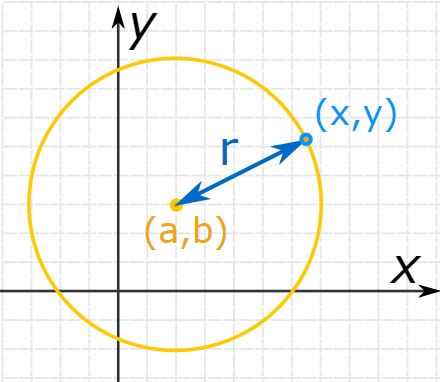
با توجه به شکل بالا، فاصله تمامی نقاط روی دایره تا نقطه (a,b) برابر با r است. بنابراین جهت نوشتن رابطه فیثاغورس،‌ مثلثی قائم‌الزاویه را مطابق با شکل زیر در نظر می‌گیریم.

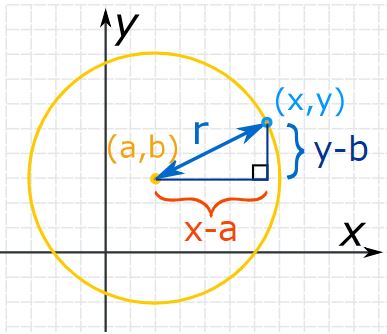
با توجه به طول‌های نشان داده شده در شکل فوق،‌ رابطه فیثاغورس را می‌توان به‌شکل زیر بیان کرد:

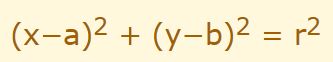
بنابراین رابطه بالا، توصیف کننده دایره‌ای است که مرکز آن در نقطه (a,b) قرار دارد.

مثال ۲

رابطه دایره‌ای به شعاع ۶ و مرکز (3,4) را بدست آورید.

همان‌گونه که بیان شد،‌ رابطه کلی یک دایره، برابر است با:

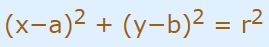
بنابراین با جایگذاری مقادیر b،a،r در رابطه بالا داریم:

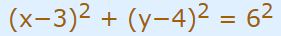
البته با استفاده از مهارت‌های ریاضیتان، می‌توانید رابطه فوق را به شکل‌های متفاوتی بیان کنید.

شناسایی رابطه دایره

توجه داشته باشید که ممکن است با رابطه‌ای مواجه شوید که در ظاهر نشان دهنده یک دایره نباشد. جهت توضیح بیشتر،‌ رابطه‌ای را مطابق با عبارت زیر در نظر بگیرید.

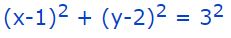
رابطه فوق، توصیف کننده دایره‌ای به شعاع ۳ و مرکز (1,2) است. از طرفی رابطه فوق را می‌توان به شکل زیر باز کرد.

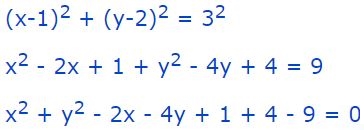
بنابراین با محاسبه رابطه بالا،‌ نهایتا شکل معادله برابر با عبارت زیر بدست آورد.

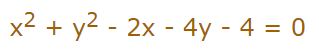
همان‌گونه که نشان داده شد، رابطه فوق نشان دهنده معادله دایره است،‌ اما در نگاه اولیه نمی‌توان آن را تشخیص داد. بنابراین در هنگام مواجه با رابطه‌ای به شکل بالا،‌ در ابتدا بایستی در مورد دایره بودن یا نبودن آن تفکر کرد.

با توجه به نمونه بالا،‌ معادله عمومی نشان دهنده یک دایره مطابق با رابطه زیر قابل تعریف است.

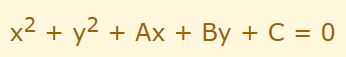
توجه داشته باشید که در رابطه مربوط به دایره همواره عبارات x² و y² ظاهر می‌شوند.

ساده کردن رابطه عمومی دایره

همان‌گونه که در بالا نیز بیان شد، رابطه عمومی نشان دهنده دایره به‌شکل زیر است.

رابطه فوق را می‌توان به شکل استاندارد، برابر با رابطه زیر بیان کرد:

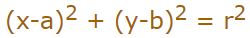
جهت نحوه بدست آوردن شکل استاندارد یک رابطه،‌ توجه شما را به مثال زیر جلب می‌کنیم.

مثال ۳

رابطه زیر نشان دهنده یک دایره است. با توجه به این رابطه،‌ شعاع و مرکز آن را بیابید.

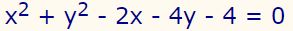
در ابتدا بایستی ضرایب x و y را مشابه با عبارت زیر بیان کرد (ضرایب x کنار یکدیگر و ضرایب y نیز کنار هم قرار گیرند):

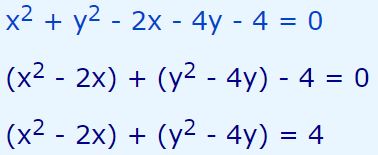
رابطه فوق، به شکل زیر قابل بیان کرد:

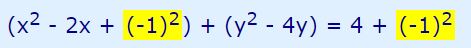
همانند بالا، جهت نوشتن توان دوم y نیز عدد ثابت ۴ را به طرفین رابطه بالا اضافه می‌کنیم. بنابراین داریم:

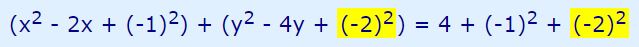
بنابراین شکل استاندارد رابطه ارائه شده در صورت سوال، برابر است با:

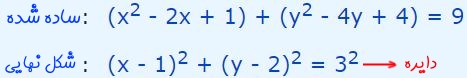
در نتیجه مرکز و شعاع دایره مرتبط با رابطه ارائه شده در صورت سوال، به‌ترتیب برابر با (۱,2) و ۳ است.

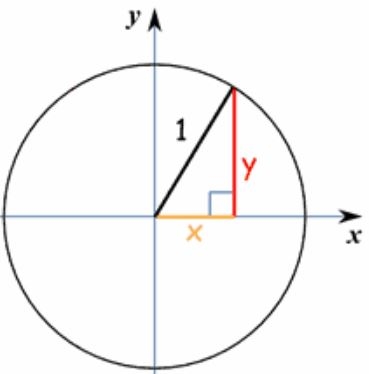
دایره واحد

اگر دایره‌ای به شعاع ۱ و با مرکز (0,0) رسم شود، رابطه مربوط به آن برابر است با:

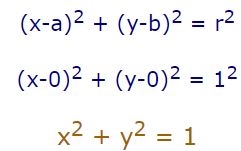
به دایره مذکور، دایره واحد گفته می‌شود.

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

این دایره در شکل زیر رسم شده است.