نامساوی چبیشف – کاربرد در توزیعهای غیرنرمال
اغلب در انجام محاسبات آماری، مواردی پیش میآید که دادهها توزیع نرمال ندارند. به این ترتیب بیشتر پیشفرضهای مربوط به تجزیه و تحلیلها برآورده نشده و نتایج حاصل از آنها ممکن است باعث گمراهی تحلیلگر شود. سوالی که اینجا پیش میآید این است که اگر دادهها توزیع نرمال نداشته باشند، چه باید کرد؟ در حقیقت به دنبال روشهایی هستیم که بتوان تحلیلهای آماری را برای توزیعهای غیر نرمال انجام داد. کاربرد نامساوی چبیشف و دیگر نامساویهایی که برمبنای احتمال نوشته میشوند میتواند به عنوان مبنای تحلیلهای جایگزین در زمان نرمال نبودن دادهها، باشد.

برای درک بهتر این مطلب، پیشنهاد میشود مطلب توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها و توزیع نرمال و توزیع نرمال استاندارد — به زبان ساده را قبلا مطالعه کرده باشید. البته خواندن نوشتار امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها نیز خالی از لطف نیست.
کاربرد نامساوی چبیشف
در این نوشتار به بررسی نامساوی و کرانهای چبیشف در تحلیل دادههای آماری میپردازیم. اگر شرط نرمال بودن دادهها وجود نداشته باشد، استفاده از این نامساوی و کرانهایش، میتواند ملاکی برای نمایش میزان تراکم و یا پراکندگی دادهها حول میانگین ارائه دهد.
هنگامی که مشخص شود که توزیع دادهها نرمال هستند، دریچهای بس زیبا و دلچسب برای انجام تحلیلهای آماری به روی تحلیلگران باز میشود و میتوانند از روشها و تکنیکهای بسیاری بهره ببرند که دقیق و قابل درک هستند. در عین حال ممکن است که شرط نرمال بودن برای مجموعه داده برقرار نباشد. آنگاه این دریچه زیبا، تبدیل به تنگنایی بس وحشتناک و دلهرهآور خواهد شد و توزیع دادهها به شکل ترسناکی در مقابل تحلیلگر ظاهر و حتی به یک کابوس هراسآور تبدیل میشود.

برای آنکه درک کنیم، شرط نرمال برای توزیع دادهها چقدر اهمیت دارد، در زیر به بعضی از تحلیلها و تکنیکهای آماری اشاره میکنیم که بدون وجود چنین شرطی، اجرای آنها امکانپذیر نیست. یعنی انجام این روشها، به جای نتایج صحیح و ارزشمند، گمراهی و کجفهمی نصیبمان میکند.
- تکینکهای شش سیگما در کنترل کیفیت آماری
- قواعد ۶۸-۹۵-۹۹.۷ که درصد دادهها را برای یک، دو و سه برابر انحراف استاندارد فاصله از میانگین، نشان میدهند.
- استفاده از آزمونهای فرض آماری با توجه به توزیع نرمال
توزیع نرمال، فراگیر و همه جانبه
توزیع نرمال یا توزیع گاوسی یکی از معمولترین و مهمترین توزیعهای آماری است که به طور گسترده در همه جا به کار گرفته میشود. یکی از دلایلی که میتواند اهمیت وجود توزیع نرمال برای دادهها را نشان دهد، وجود پدیدهها و متغیرهای زیادی است که بخصوص در روانشناسی، فیزیک و ... از توزیع نرمال پیروی میکنند. میزان قدرت خواندن، رضایت شغلی و حافظه که در روانشناسی و مباحث آموزشی اندازهگیری میشوند، دارای توزیع نرمال یا تقریبا نرمال هستند.
از طرف دیگر وجود قضیههای متعدد برای این توزیع، باعث بوجود آمدن تکنیکهای سادهای شده است که امکان تجزیه و تحلیل روی دادههایی با توزیع نرمال را فراهم میسازند. همچنین وجود قضیه حد مرکزی، میتواند تضمین کند که برای نمونههای به اندازه کافی بزرگ، توزیع مجموع یا میانگین متغیرهای تصادفی هم توزیع و مستقل با میانگین و واریانس ثابت، به سمت توزیع نرمال میل میکند.
همه این دلایل، اهمیت و قدرت تحلیلهای آماری براساس توزیع نرمال را نشان میدهد. ولی در صورتی که دادهها توزیع نرمال یا شرایط قضیه حد مرکزی را نداشته باشند، استفاده از چنین تحلیلهایی امکانپذیر نیست. اغلب ممکن است در کار تحلیل دادهها در «علم داده» (Data Science) به مواردی برخورد کنید که شرایط توزیع نرمال برای اطلاعات جمعآوری شده، وجود نداشته باشد. این اتفاق در تحلیل دادههای مربوط به کسب و کار در زمینههای مختلف، ممکن است، رخ دهد.
فرض کنید به یک سری داده جدید برخورد کردهاید و میخواهید بدانید که آیا آنها معنیدار هستند. در اینجا معنیدار بودن به این شکل بیان میشود که آیا دادهها در کرانهای مورد انتظار شما، قرار دارند یا خیر. معمولا در ابتدای کار تحلیل دادهها، میانگین و انحراف استاندارد دادهها را محاسبه میکنیم تا نسبت به آنها شناخت بیشتری پیدا کنیم. در ادامه بررسی میکنیم که دادههای جدید در چه فاصلهای از میانگین برحسب انحراف استاندارد قرار میگیرند و یا انتظار است چه درصدی از دادهها در فاصلهای خاص قرار گرفته باشند. اگر قرار است در سطح اطمینان ۹۵٪ تجزیه و تحلیلها را انجام دهیم، انتظار داریم که ۹۵٪ دادهها در فاصله دو انحراف استاندارد از میانگین قرار داشته باشند.
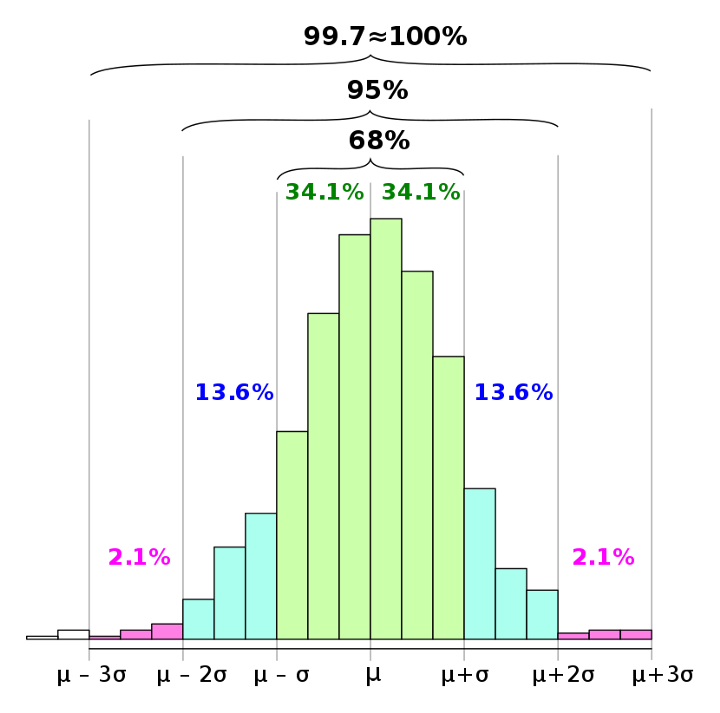
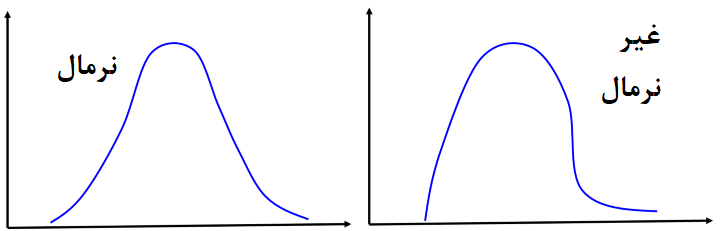
همانطور که در تصویر بالا دیده میشود، در حدود 99.7٪ از دادهها در محدوده سه انحراف استاندارد بیشتر و کمتر از میانگین قرار دارند. این قاعده که به قانون «شش سیمگا» (Six- Sigma) معروف است با توجه به فرض نرمال بودن جامعه (نه فقط نمونه آماری) بوجود آمده است. اما اگر این شرط برقرار نباشد، یعنی توزیع جامعه آماری، نرمال نباشد، چه اتفاقی خواهد افتاد؟ درست به حالت تصویر سمت راست که چولگی زیادی را نشان میدهد.
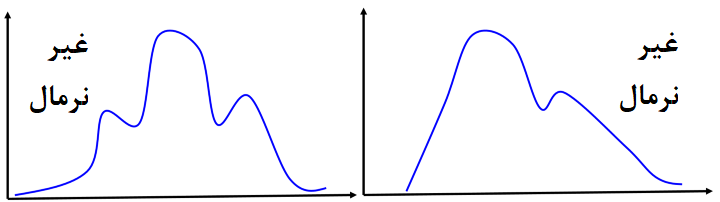
یا اگر توزیع دادهها به صورت زیر باشد، برای پیدا کردن کرانها چه باید کرد؟ مشخص است که این توزیعها دارای چند قله هستند.
استفاده از نامساوی چبیشف و کرانهای آن
همانطور که دیده میشود، مشکل اصلی، هنگام کار با دادههایی است که از توزیع نرمال پیروی نمیکنند و به این علت قاعده شش سیمگا ناکارآمد خواهد بود و در نتیجه نمیتوان حدود تغییرات دادهها را پیشبینی کرد. برای مثال نمیتوان گفت که در فاصله میانگین و یک انحراف استاندارد، حدود 34.1٪ از مشاهدات وجود دارد.
در حقیقت ما به دنبال راه حلی هستیم که به کمک آن بتوان عبارت زیر را بیان کرد: «احتمال آنکه یک داده از مشاهدات جدید در یک فاصله مشخص از میانگین قرار داشته باشد برابر است با ...»
خوشبختانه کرانهای نامساوی چبیشف قادر است مشکل را برطرف کند. این نامساوی به افتخار دانشمند روسی «پافنوتی چبیشف» (Pafnuty Chebyshev) نامگذاری شده است. او در سال 1853 اثبات این نامساوی را ارائه و منتشر کرد.
نامساوی چبیشف (Chebyshev Inequality)
فرض کنید X یک متغیر تصادفی با امید ریاضی و واریانس متناهی باشد. آنگاه برای هر عدد حقیقی مثبت مثل k داریم:

این نامساوی نیز با توجه به واریانس و امید ریاضی توزیع، یک کران بالا برای تابع احتمال متغیر تصادفی X در دمهای سمت راست ایجاد میکند.
این نامساوی تضمین میکند که برای همه توزیعهای احتمالی، درصدی از مقادیر که بیشتر از فاصله مشخصی از میانگین قرار داشته باشند از قاعده خاصی پیروی میکند و دارای یک کران بالا است. به بیان دیگر این نامساوی نشان میدهد که احتمال آنکه مقداری بیش از k برابر انحراف استاندارد () از میانگین دور باشد حتما کمتر از خواهد بود. برعکس، احتمال آنکه فاصله مقداری از میانگین از k برابر انحراف استاندارد، کمتر باشد بیشتر از است.
از آنجایی که این نامساوی بدون فرض نرمال بودن توزیع ایجاد شده است، از آن برای پیدا کردن کرانها برای دادههایی با هر توزیع احتمالی، میتوان استفاده کرد. به این ترتیب بدون آگاهی از مکانیزم تولید یا توزیع دادهها میتوان گفت: «من با اطمینان ۷۵٪، میدانم که دادهها در فاصله ۲ انحراف استاندارد از میانگین قرار دارند.»
یا عبارتی مانند زیر را برای فاصله سه انحراف معیار بیان کرد: «با اطمینان ۸۹٪، دادههای در فاصله سه انحراف استاندارد از میانگین قرار دارند.»
همانطور که دیده میشود، به این شکل میتوان حدود شش سیگما را برای هر توزیعی محاسبه و نمایش داد. این حدود برای یک توزیع دلخواه در تصویر زیر نمایش داده شده است.
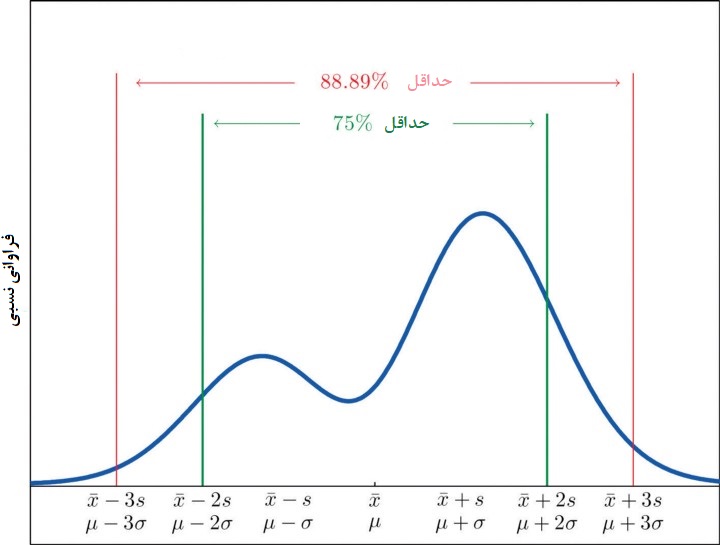
همانطور که دیده میشود، اصل محاسبات برای دادهها تغییری نکرده است و همچنان میانگین و انحراف استاندارد را برای دادهها محاسبه میکنیم. ولی برای تعیین احتمالات یا درصدی از دادهها که در یک محدوده قرار دارند، باید از نامساوی چبیشف استفاده شود. بنابراین مراحل کار به صورت زیر خواهد بود:
- جمعآوری دادههای نمونهای از یک جامعه آماری با توزیع نامشخص (غیر نرمال)
- محاسبه میانگین و انحراف استاندارد براساس نمونه
- محاسبه کرانهای چبیشف
جدول زیر به بررسی کرانهای چبیشف براساس ضرایب انحراف استاندارد به عنوان فاصله از میانگین پرداخته است. همانطور که مشخص است، ستون اول مقدار k را نشان میدهد که بیانگر مضربی از انحراف استاندارد است که در نامساوی چبیشف به کار میرود. ستون دوم نیز حداقل احتمال را برای مقدارهایی نشان میدهد که فاصلهای کمتر از k انحراف استاندارد از میانگین دارند. همچنین ستون سوم نیز همان نامساوی چبیشف است که حداکثر احتمال را برای مقدارهایی نشان میدهد که k انحراف استاندارد از میانگین دورتر هستند.
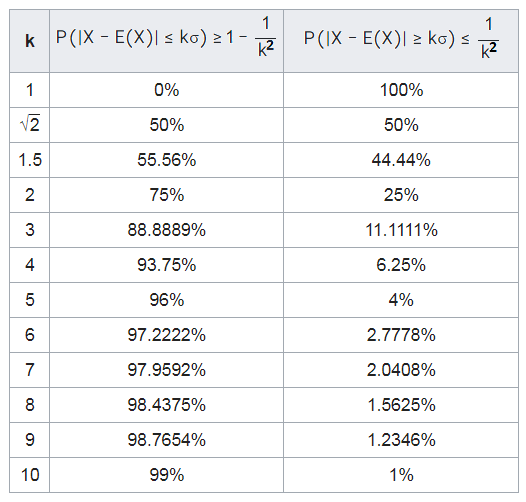
نکته: مجموع ستون دوم و سوم در هر سطر باید برابر با ۱ باشد.
برای مثال میتوان براساس سطر آخر ستون دوم گفت که ۹۹٪ دادهها حداکثر ۱۰ برابر انحراف استاندارد از میانگین فاصله دارند و یا ۱٪ دادهها، بیشتر از ۱۰ برابر انحراف استاندارد از میانگین دور هستند. این فاصله ۱۰ برابری را با فاصله ۳ برابری در توزیع نرمال مقایسه کنید.
همچنین در سطر پنجم میتوان گفت که ۹۶٪ دادهها فاصلهای کمتر از ۵ برابر انحراف استاندارد از میانگین دارند. از طرف دیگر ۴٪ دادهها نیز بیش از ۵ برابر انحراف استاندارد از میانگین فاصله دارند. به همین ترتیب با توجه به توزیع نرمال، دیده میشود که 4٪ دادهها در فاصله بیش از ۲ برابر انحراف استاندارد از میانگین فاصله دارند.
دقت در کرانهای چبیشف
با مقایسه نمودار مربوط به کرانهای چبیشف و کرانهای نرمال، کاملا مشخص است که دقت در این کرانها کمتر از حالت نرمال است. یعنی اگر فرض کنیم که دادهها توزیع نرمال داشته باشند، فاصله بین دو انحراف استاندارد از میانگین شامل 95٪ دادههاست در حالیکه با استفاده از نامساوی چبیشف چنین فاصلهای فقط شامل 75٪ دادهها است. این موضوع نشان میدهد که در محاسبه کرانهای چبیشف جانب احتیاط حفظ شده و طول فاصلهها باید بسیار بزرگتر از حالت نرمال باشد تا ۹۵٪ دادهها را پوشش دهد. همانطور که در جدول نیز دیده میشود، در صورتی که k برابر با ۵ باشد، میتوان حدود ۹۵٪ دادهها را در فاصله ۵ انحراف استاندارد از میانگین در نظر گرفت که با k=2 در حالت شش سیگما بسیار اختلاف دارد.
به این ترتیب میتوان گفت: «قاعده چبیشف و نامساوی آن نسبت به قاعده شش سیگما برای توزیع نرمال بسیار ضعیفتر برای تعیین کرانها است.»
با همه این مشکلات، زمانی که توزیع دادهها مشخص نباشد، استفاده از نامساوی چبیشف میتواند در تعیین کرانها برای احتمال چاره ساز باشد.
البته نامساوی و کرانهایی دیگری مانند «کرانهای چرنوف» (Chernoff Bound) یا «نامساوی هوفدینگ» (Hoeffding Inequliaty) میتوانند کرانهای تیزتری نسبت به نامساوی چبیشف ارائه دهند و از دقت بالاتری نیز برخور دارند ولی ممکن است شرایط یا محاسباتی پیچیدهتری داشته باشند.
به این ترتیب به نظر میرسد که داشتن توزیع نرمال یا تقریبا نرمال برای دادهها دقت انجام محاسبات را بالا میبرد ولی در صورتی که دادهها توزیع نرمال نداشته باشند، روشهایی وجود دارد که انجام استنباط آماری را برای تحلیلگرهای علم داده میسر میسازد. زمانی که اطلاعات بسیار محدود و کمی از توزیع دادهها در اختیار داریم، نامساویهای چبیشف و هوفدنیگ میتوانند کرانهای نسبتا دقیقی برای پیشبینی حدود دادههای جدید از جامعه آماری به ما بدهند و این کار تنها از طریق محاسبه میانگین و انحراف استاندارد دادهها میسر میشود.
اگر به فراگیری مباحث مشابه مطلب بالا علاقهمند هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزشهای نرمافزارهای آماری
- آموزش آمار و احتمال مهندسی
- توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
- توزیع نرمال و توزیع نرمال استاندارد — به زبان ساده
- امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها
^^













اقای دکتر سلام تشکر بابت راهنمایی ها و سایت خوبتون
می خواستم بدونم برای محاسبه آماره های میانگین و … در جامعه غیر نرمال با تعداد بسیار بالا چه روشی رو می توانیم استفاده کنیم؟؟
که با دقت بالا بتوانیم به آن استناد کنیم.
واقعا سایتتون عالیه
با عرض سلام و تشکر از شما
در بخشی از متن آمده است «…که برمبنای توزیع نرمال عمل میکنند.» گمانم این عبارت باید تبدیل شود به «… که بر مبنای توزیع نرمال عمل نمی کنند.»
با تشکر از تذکر سازنده شما؛ متن قبلی شاید کمی گنگ به نظر میرسید… بنابراین جمله مورد نظر اصلاح شد، ولی منظور این بود که از نامساوی چبیشف زمانی که تحلیلهای برمبنای نرمال کاربردی ندارند میتوان استفاده کرد.
باز هم ممنون و تشکر از توجه شما.
سلام وقت بخیر
ضمن تشکر از جناب آقای آرمان ری بد
از شما تقاضا دارم مطالب بیشتری از بلاگ فرادرس را به امار اختصاص بدهید نظر شخصی من این است هوش مصنوعی یادگیری ماشین و … بدون دانش امار خیلی سخت است امار پایه ای اساسی برای ورود به این مباحث است.
باتشکر