مفاهیم مقدماتی حسابان (بخش پنجم) – به زبان ساده
در بخش قبلی این سری مطالب آموزش مفاهیم مقدماتی حسابان به جمعبندی درک شهودی مطرح شده از حسابان پرداختیم.

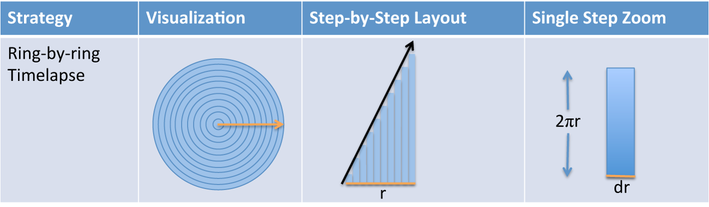
بدین ترتیب ابتدا با استفاده از بینش شهودی خود متوجه شدیم که میتوانیم یک دایره را به قطعاتی تقسیم کنیم تا مساحت آن را سادهتر به دست آوریم. سپس دایره را به حلقههایی از مرکز به سمت بیرون تقسیم کردیم. این وضعیت در تصویر زیر قابل مشاهده است:
همچنین متوجه شدیم که توصیف رسمی این کار که انتگرال نام دارد به صورت زیر است:
- 2 ضرب در عدد پی ضرب در r ضرب در dr را از r=0 تا r=r جمع بزن.
معادل انگلیسی این تعریف به صورت زیر است:
- integrate 2 * pi * r * dr from r=0 to r=r
باید بدانید که تعریف رسمی ما از این محاسبه آن قدر دقیق است که میتوانیم با ارائه آن به یک رایانه انتظار داشته باشیم مسئله ما را حل کند. برای نمونه در تصویر زیر از موتور دانش محاسباتی wolframalpha برای حل این مسئله استفاده کردهایم:
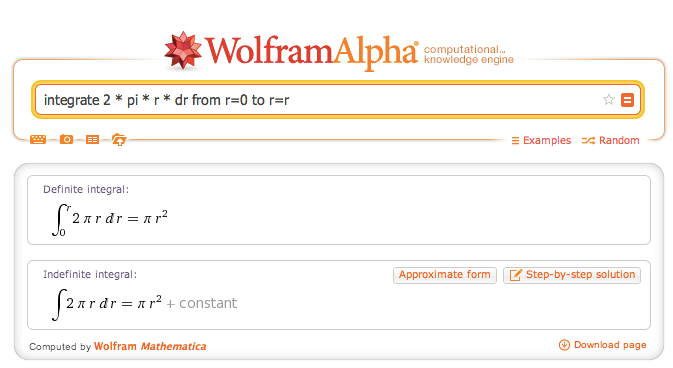
بنابراین همان طور که میبینید ما موفق شدهایم تفکر شهودی خود را چنان جمعبندی و بیان کنیم که یک رایانه بتواند منطق کار را اجرا کند. بدین ترتیب دیگر لازم نیست حلقههای یک دایره را به صورت دستی باز کنیم، یک مثلث بکشیم و مساحت آن را بیابیم. ما میتوانیم مراحل را مانند روش فوق بنویسیم و با ارائه آن به رایانه منتظر نتیجه باشیم.
اینک نوبت به بررسی مشتق میرسد. ما برای توصیف این عملیات از رویکرد اشعه ایکس در بخشهای قبلی این سری مطالب آموزشی استفاده کردهایم. ما میتوانیم تعریف رسمی همین رویکرد را نیز به رایانه ارائه کرده و از آن جواب بگیریم.
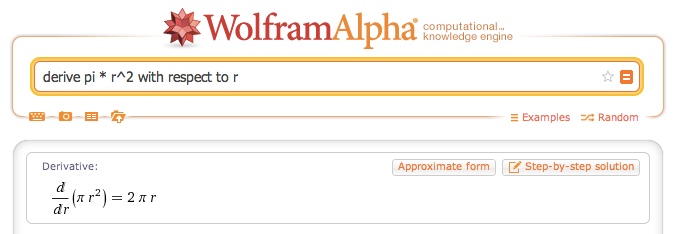
مانند حالت فوق، رایانه فرمول را برای مساحت به صورت اشعه ایکس محاسبه میکند و آن را به صورت مرحله به مرحله افراز میکند. نتیجه برابر با 2πr است که ارتفاع دایره در هر نقطه را نشان میدهد.
بررسی عملی اصطلاحات
Wolfram Alpha ابزاری با استفاده آسان است. قالب کلی معادلات حسابان (به ترتیب انتگرال و مشتق) به صورت زیر است:
- [integrate [equation] from [variable=start] to [variable=end
- [derive [equation] with respect to [variable
در عبارت فوق از کلمات زیادی استفاده شده است. بنابراین میانبرهای زیر به نمادهای ریاضیاتی نزدیکتر هستند:
- int [equation] dr\ - معادله انتگرال (به طور پیشفرض، فرض میکنیم که از r=0 به r=r که مقدار بیشینه است، حرکت میکنیم)
- d/dr equation – از معادله با توجه به r مشتق میگیریم.
- میانبرهای برای توان (3⌃2 = 9)، ضرب (3 * r) و جذر (sqrt(9) = 3) وجود دارد.
اینک که میانبرهای محاسباتی مورد نیاز را داریم چند نتیجه را که تا به اینجا به دست آوردهایم بررسی میکنیم:
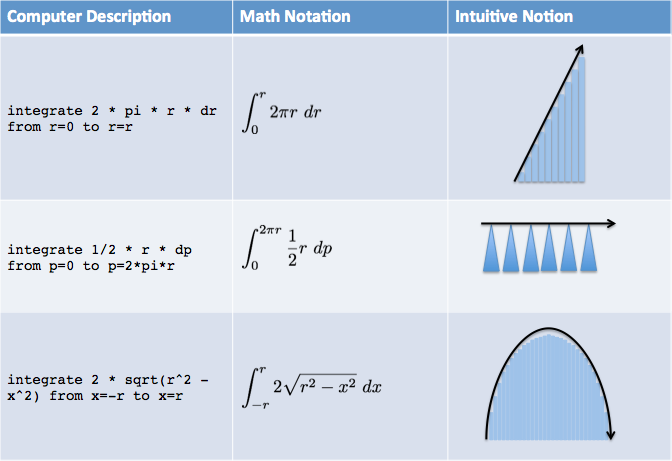
با کلیک روی تعریف رسمی ارائه شده میتوانید ببینید رایانه محاسبات عددی مربوطه را ارائه میکند. همان طور که انتظار داریم همه تعاریف فوق همان فرمول مساحت آشنا را به دست میدهند. در ادامه به چند نکته اشاره میکنیم:
اندازه گوهها به صورت ½ قاعده × ارتفاع است. قاعده برابر با dp (بخش کوچک محیط) و ارتفاع برابر با r است. فاصله از محیط تا مرکز محاسبه میشود.
اندازه برش کمی پیچیدهتر است. برحسب مختصات x و y و بر اساس قضیه فیثاغورس معادله را داریم:
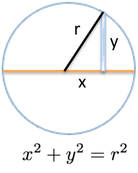
ما معادله فوق را برای ارتفاع حل میکنیم تا به فرمول برسیم. در واقع به دو کپی از ارتفاع نیاز داریم، زیرا y مسافت مثبت بالای محور مختصات است و برشها به سمت بالا و پایین آن امتداد مییابند. کار با برشها دشوارتر است و این اختصاص به ما ندارد و موتور «ولفرام آلفا» نیز برای محاسبه آن به زمان بیشتری نیاز دارد.
سخن پایانی
رویکرد ما در این نوشته تا به اینجا مبتنی بر این واقعیت بوده است که تا جای امکان شما را با طرز فکر حسابان آشنا کنیم و به تدریج نمادها را به شما معرفی کنیم. برخی از این نمادهای ریاضیاتی گیجکننده هستند که دور از انتظار نیست. این وضعیت مانند آن است که در کافهای نشسته باشید و مکالمات میز کناری به زبانی بیگانه را گوش دهید. در بخشهای بعدی این سری مطالب راهنمای جامع حسابان نیز با ما همراه باشید تا جزییات همه این مفاهیم را به صورت گام به گام با هم مرور کنیم.
برای مطالعه بخش بعدی این مطلب روی لینک زیر کلیک کنید:
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- انتگرال — به زبان ساده
- آموزش جامع حساب دیفرانسیل و انتگرال پیش دانشگاهی
- انتگرال و روش های محاسبه — به زبان ساده
- انتگرال توابع مثلثاتی — از صفر تا صد
- آموزش مشتق گیری و انتگرال گیری عددی در محاسبات عددی
==












